圆锥（台）形人造山体地基竖向附加应力及沉降

2020-07-29高彦斌姚天骄

同济大学学报（自然科学版） 2020年7期

高彦斌，姚天骄

（同济大学土木工程学院，上海200092）

现代化城市建设中，园林绿化、生活垃圾和工业废料堆填等人造山体工程逐渐增多，且山体高度逐渐增大。为了区别于自然界中的山体，这里将之统称为人造山体。人造山体大多数可近似看作圆锥形或圆台形，属于轴对称形态，其产生的荷载与建筑工程中常见的矩形或条形荷载差别较大。在山体地基沉降计算分析中，竖向附加应力分析是最为关键的内容。自1885 年首次提出后，布辛涅斯克弹性解（简称布氏解）被广泛应用于求解各种类型荷载下的地基竖向附加应力以及地表沉降，具体包括条形均布荷载［1］、三角形条形荷载［1-2］、堤坝形或梯形条形荷载［2-3］、矩形荷载［4-7］。相关研究有的给出计算公式，有的则仅给出计算图表。这些研究成果至今应用于荷载类型较为简单的基础、路基、坝基工程的地基竖向附加应力以及沉降计算中。然而，当荷载形式和边界条件较为复杂时，往往难以得到竖向附加应力解析解，这种情况下通常需要借助数值分析方法。近年来，采用布氏解以及弹性有限元法，针对抛物线路堤荷载［8］、飞机荷载［9-10］、输油管道荷载［11］、高填方渠道［12］等具有复杂荷载和边界条件的地基附加应力和地基沉降的研究取得了较多成果。对于轴对称荷载（山体荷载），只有少数学者基于布氏解对其地基竖向附加应力进行了研究。Harr等［13］最早给出了几种轴对称荷载下（抛物线形荷载、圆形均布荷载、圆锥形荷载）地基中心竖向附加应力的解析解，但并未对比分析其具体特征。对于轴对称荷载下任意位置的竖向附加应力以及地表沉降，角点法不再适用；由于求解的复杂性，目前仍未获得解答。因此，在分析这类荷载下任意位置的地表沉降以及相邻荷载之间的相互影响方面，至今仍然存在较大的困难，缺乏系统的研究成果。目前工程界（包括行业规范）普遍忽略这类荷载的特殊性，仍采用条形荷载来分析轴对称山体地基的附加应力与沉降。

本文采用布氏解析法以及数值分析方法，给出轴对称山体荷载下地基的中心点竖向附加应力以及任意位置处竖向附加应力求解方法；在此基础上，讨论轴对称荷载下的附加应力分布特征和地基沉降特征，并与条形荷载的结果进行对比，解决该类荷载下地基沉降计算中的一些问题。

1 布辛涅斯克解的应用及问题

1.1 求解竖向附加应力

1885 年，布辛涅斯克给出了竖向集中力作用于均匀各向同性弹性半无限空间表面情况下，弹性体内某一点M（x，y，z）的竖向附加应力解［14］，即

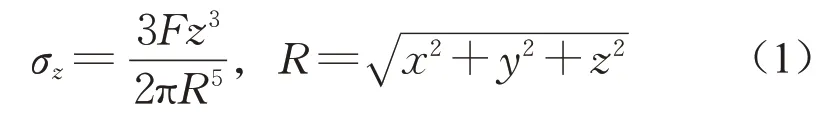
式中：σz为深度为z处的竖向附加应力；F为集中荷载的大小；R为计算点与荷载作用点连线的长度。

从式（1）可以看出，附加应力解与弹性介质的参数无关。对于图1所示的半无限空间表面作用分布荷载p（ζ，η）的情况（ζ和η为荷载作用点坐标），为计算某点M（x，y，z）的竖向附加应力σz，可以取一微单元，其面积 dA=dζdη，微单元荷载为 dF=p（ζ，η）·dζdη，这样弹性体中M点的竖向附加应力σz可用以下积分式求得：

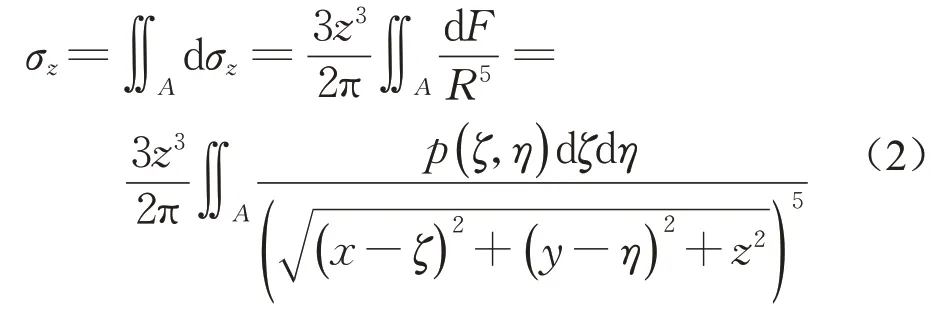
这样，各种类型荷载作用下地基竖向附加应力公式可根据荷载形式由式（2）积分求得，差异仅在于等效集中力dF。

1.2 求解地表沉降

如图1所示，集中力F作用下弹性体中任意一点M（x，y，z）的竖向位移w为

图1 集中和分布荷载作用下土中应力计算Fig.1 Calculation of stress in soil under concentrated and distributed loads

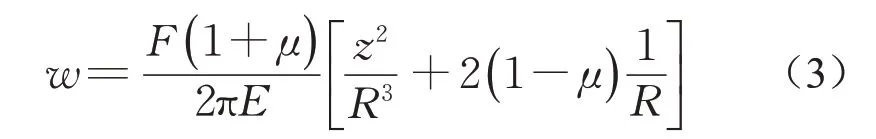
式中：E、μ分别为弹性体的弹性模量和泊松比。对于图1所示的半无限空间表面作用分布荷载p（ζ，η）的情况，采用式（3）可得到微单元荷载dF作用下半无限空间表面（z=0）的地表沉降ds的表达式为

对荷载作用面积上进行积分就可得到分布荷载p（ζ，η）作用下的地表沉降为

需要说明的是，对于有限面积内的分布荷载（如矩形、圆形荷载），采用式（5）可以得到一个确定的沉降；但对于无限面积的分布荷载（如条形荷载）采用式（5）得到的沉降随着计算深度的增大而无限增大。

1.3 求解中的问题

由于涉及到积分运算，在利用布氏解求解不同类型的荷载下的附加应力时，能否直接给出解析解取决于荷载的表达式，即式（2）和式（5）中的p（ζ，η）。在不能直接给出解析解的情况下，则需要采用数值积分方法给出其解答，或者采用有限元等数值分析方法计算得到附加应力。相比来讲，有限元等数值分析方法具有更广泛的适用性，可以给出任意荷载形态下的附加应力，但一般以图表的形式给出，而不能给出附加应力的数学表达式。

应用式（5）进行地表沉降计算时会出现两种情况。对于局部荷载，附加应力随深度的增加收敛，压缩层厚度有限，表现为式（5）有解；对于无限长条荷载，其附加应力随深度增加不收敛，因此式（5）无解，其沉降弹性解常以相对沉降（即计算点沉降与中心点沉降之差）表示。例如Gibson［15］提出的长条均布荷载在均匀半无限体上引起的相对沉降公式。

2 圆锥（台）荷载下竖向附加应力

2.1 中心点竖向附加应力系数

为便于分析研究，本文将常见的轴对称山体荷载及部分典型荷载示意图汇总如图2所示。

地基竖向附加应力系数定义为αz=σz/p0（p0的定义见图2）。下面采用式（2）推导圆锥（台）形人造山体荷载作用下中心点（图2中O点）竖向附加应力系数αz0。

对于图2b 所示的半径为r0、中心点荷载为p0的圆锥形荷载，距离中心点r处微单元作用力可以采用宽度为dr、半径为r的微圆环荷载来表示，即dF=p0（1-r/r0）2πrdr，根据式（2）可得

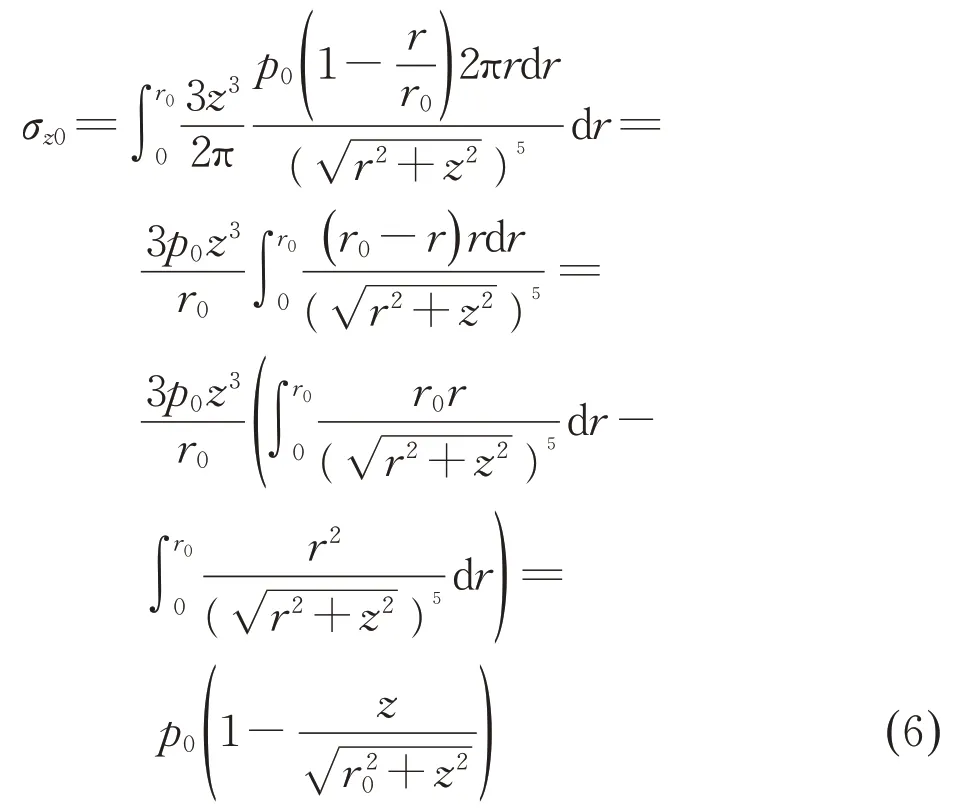
这样得到圆锥形荷载下中心点竖向附加应力系数αz0的表达式为

式（7）与Harr等［13］给出的结果是一致的。

对于图2a 所示圆台形荷载，可采用应力叠加法，由半径为r2、中心点荷载为p2的大圆锥荷载产生的附加应力减去半径为r1、中心点荷载为p1的小圆锥荷载产生的附加应力，得到圆台形荷载作用下中心点竖向附加应力为

这样得到圆台形荷载下中心点竖向附加应力系数αz0的表达式为

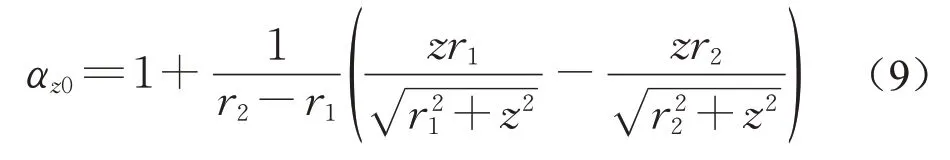
图2 几种典型荷载示意图Fig.2 Schematic diagram of several typical loads

表1 汇总了采用布氏解得到的图2 所示的5 种荷载类型中心点地基竖向附加应力系数，以便对比分析轴对称荷载作用下的地基中心竖向应力随深度的分布特征。将表1 所列公式绘制成图3 所示的αz0与深度比z/r0或z/b的关系曲线，其中圆台形荷载取r2/r1=2.0，梯形条形荷载取a/b=0.5。

表1 不同类型荷载中心点竖向附加应力系数Tab.1 Vertical additional stress coefficients at center of different loads

可以看出，表1所示5种荷载中心点竖向附加应力均随深度的增大而减小，但减小的速率不同。3种轴对称荷载（圆形、圆锥形、圆台形）中心点竖向附加应力衰减速度整体上大于两种无限长条分布荷载（三角条形、梯形条形）的衰减速度，其中圆锥形荷载衰减最快，梯形条形荷载衰减最慢。对于圆台形荷载，虽然仅给出了r2/r1=2.0 情况下的计算结果，但是可以结合图中给出的圆锥形的和圆形均布的结果来预估圆台形荷载作用下中心点竖向附加应力系数所处的范围，也就是图3中的阴影部分。

根据图3 给出的结果，不同荷载类型下竖向附加应力的影响深度差别也较大。在相同荷载水平p0下，圆锥形荷载的影响深度最小，梯形条形荷载影响深度最大。

如果以σz=0.1p0（即αz0=0.1）来确定影响深度H，则圆锥形荷载和圆形均布荷载分别为2.0r和3.7r。圆台形介于二者之间，当r2/r1=2.0 时，H=2.8r；当r2/r1＞2.0 时，2.0r＜H＜2.8r；当 1.0＜r2/r1＜2.0时，2.8r＜H＜3.7r。三角条形荷载和梯形条形荷载的H分别为6.3r和9.5r。可见，圆锥形分布荷载的影响深度是最小的。

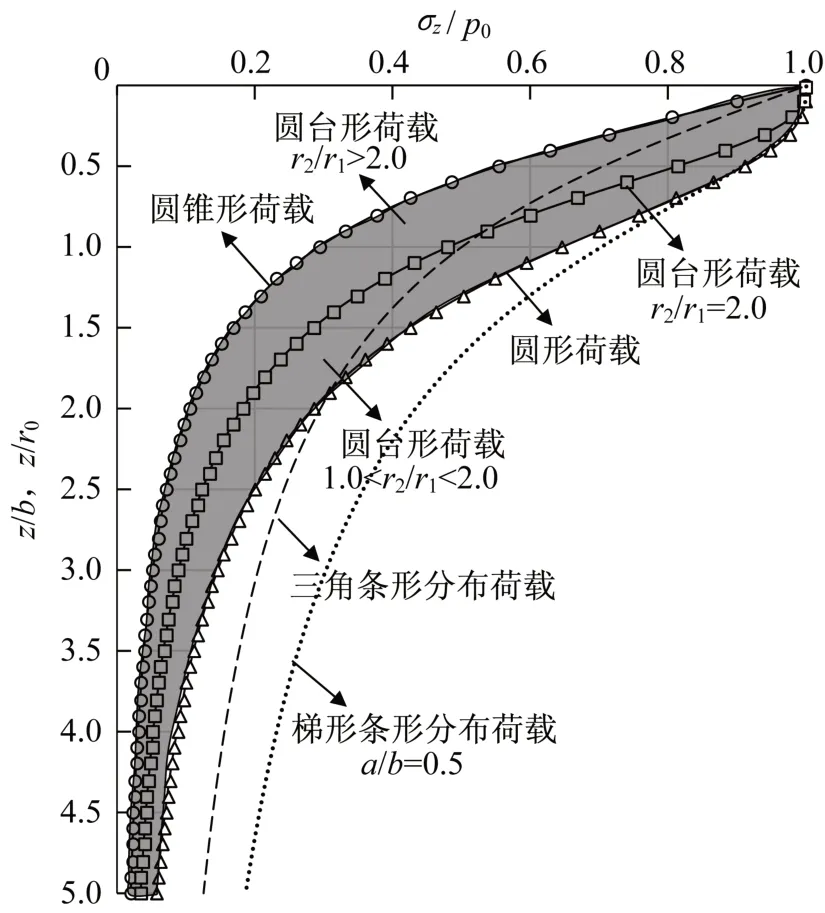
图3 不同类型荷载中心点竖向附加应力系数Fig.3 Vertical additional stress coefficients at center of different types loads

2.2 任意位置处竖向附加应力系数

对于圆锥形荷载，图2中的微单元荷载可表示为

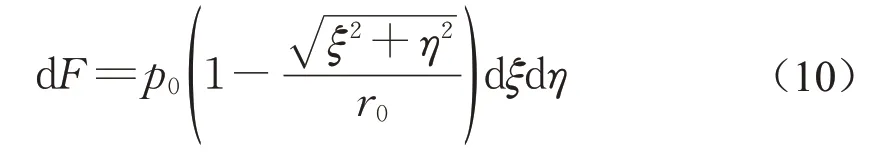
因此式（2）可表示为

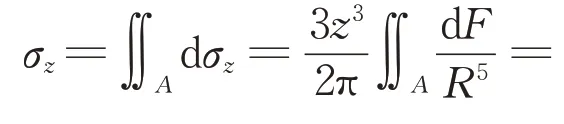
式（11）在初等函数范围内求解困难，目前尚无学者给出初等函数范围内的解析解。

这里采用弹性有限元法来获得任意位置处竖向附加应力系数。具体方法是，地基的弹性模量E和泊松比μ为某一个数值，在地基表面施加一个最大荷载p0为某一值的圆锥形荷载，求出距离荷载中心水平距离为x、深度为z处的竖向附加应力σz，然后再进一步给出附加应力系数αz=σz/p0随深度比z/r0和距离比x/r0的变化曲线，结果如图4所示。与式（1）一样，图4给出的归一化结果与弹性参数E、μ无关，即图4 给出的归一化解具有唯一性，这也是弹性分析法的一个特点［16］。有了这一结果，圆台形荷载任意位置处的竖向附加应力可通过上文所述应力叠加法，由图1a 中大圆锥的结果减去小圆锥的结果获得。

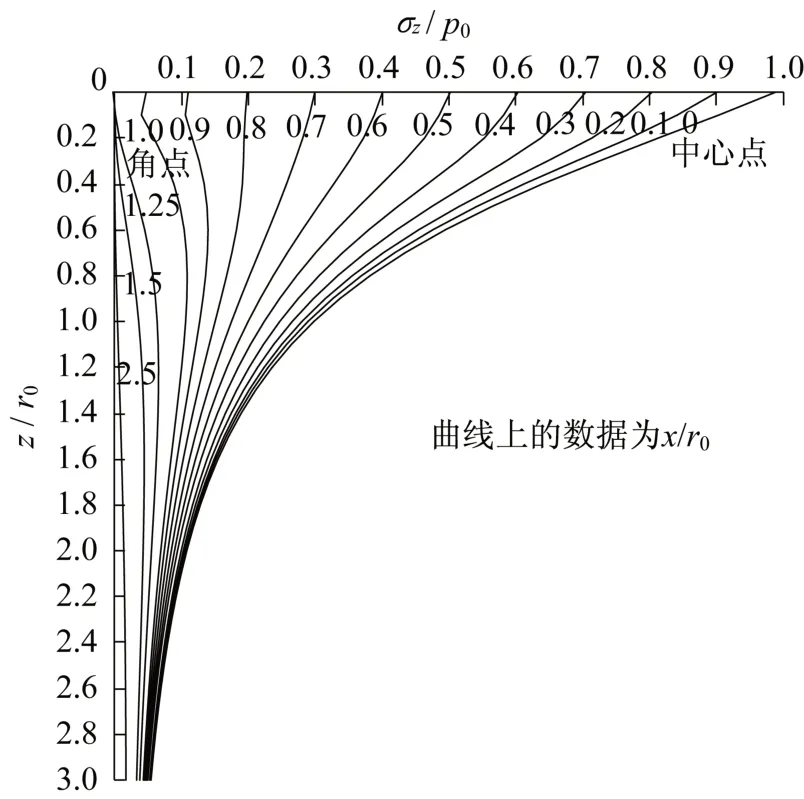
图4 圆锥形荷载任意位置处竖向附加应力系数Fig.4 Vertical additional stress coefficients at arbitrary location of conical load

为了对比分析轴对称荷载和其他形式的荷载作用下的任意位置竖向附加应力分布特征，根据式（2）推导了三角条形荷载（图1c）和梯形条形荷载（图1d）下任意位置竖向附加应力系数解析解。

三角形条形荷载为

梯形条形荷载为

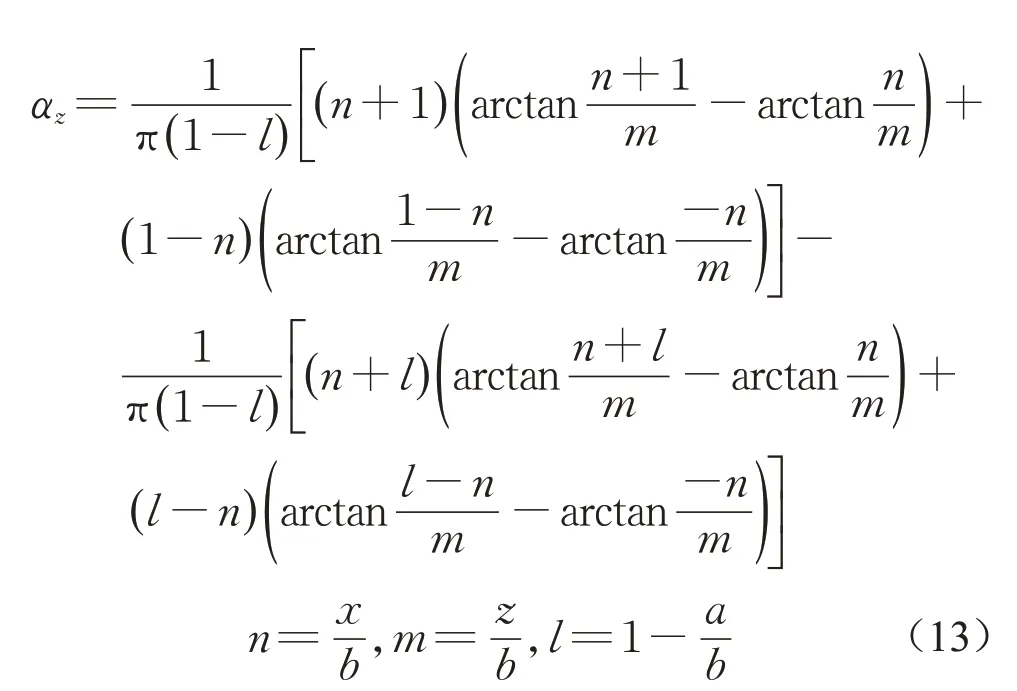
因此，本文给出的结果比已有文献给出的结果［1-3］更为简洁，应用起来更为方便。由式（12）、（13）给出的竖向附加应力系数曲线分别如图5和图6所示。

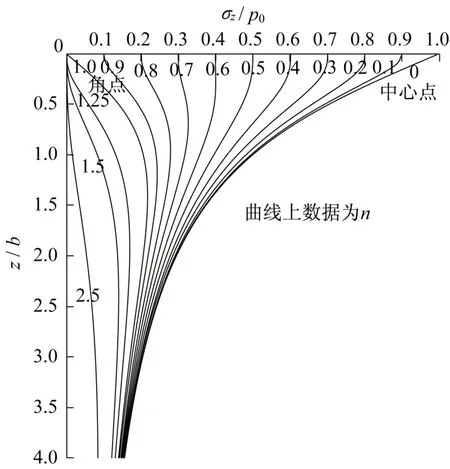
图5 三角条形荷载任意位置处竖向附加应力系数Fig.5 Vertical additional stress coefficients at arbitrary location of triangular strip load

由图4～6 可以看出，圆锥形荷载、三角条形荷载、梯形条形荷载任意位置处竖向附加应力系数曲线既有共性也有差异，可总结为以下两点：①当计算点远离荷载中心一定距离后，最大附加应力系数amax出现在地基中的某一深度而不是地表，这个深度随计算距离x的增大而增大。②圆锥形荷载的竖向附加应力随距离x的增加的衰减程度最大，荷载边缘（x/r0=1.0）处的amax约0.1p0，而三角条形和梯形条形荷载边缘处（x/b=1.0）的amax分别约为0.2p0和0.3p0。

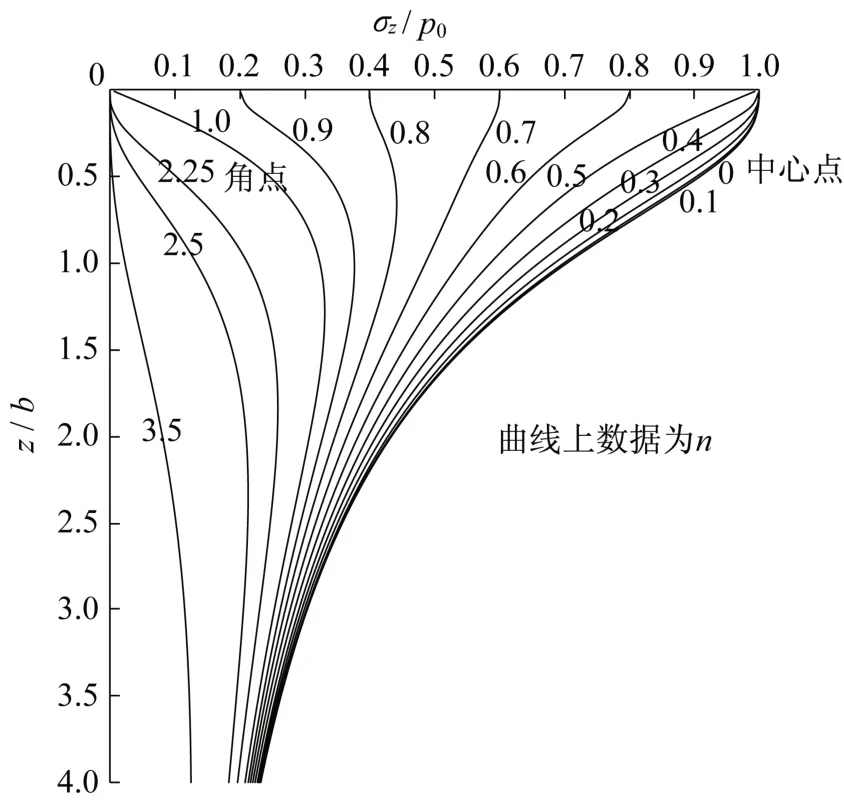
图6 梯形条形荷载任意位置处竖向附加应力系数（a/b=0.5）Fig.6 Vertical additional stress coefficients at arbitrary location of trapezoidal strip load(a/b=0.5)

由于竖向附加应力的分布决定了地基沉降，根据以上给出的附加应力随水平距离x的衰减规律，可以推断圆锥形和圆台形荷载作用下地基的不均匀沉降要大于三角条形荷载和梯形条形荷载。

3 圆锥（台）荷载作用下中心点沉降

根据式（5），圆锥形荷载作用下，距离荷载中心r、宽度为dr的微圆环荷载对中心点O产生的沉降ds为

在圆锥形荷载作用范围（0＜r＜r0）内积分，可得整个荷载作用下地基中心点沉降为

对于图2a 所示圆台形荷载，可采用变形叠加法，由大圆锥荷载产生的沉降减去小圆锥荷载产生的沉降得到。

对于有限面积荷载，各类荷载作用下地基中心点沉降可统一表示为

式中：ω0为荷载中心点沉降影响系数。

根据式（15）和式（16），以及相关文献［4］，各类荷载下的ω0值汇总如下：①圆锥形ω0=0.50；②圆形ω0=1.00；③圆台形ω0=（r2+r1）/2r2，介于圆锥形和圆形荷载之间，即0.5与1.0之间；④方形ω0=1.12；⑤均布条形ω0=4.00；⑥矩形ω0介于1.12（方形）和4.00（条形）之间，随长宽比的增大而增大。可以看出，在相同荷载水平p0和分布半径r0下，圆锥形荷载下中心点沉降最小，仅为圆形荷载的0.50 倍、方形荷载的0.45倍。

4 工程应用分析

4.1 实例分析

桃浦科技智慧城中央绿地位于上海市普陀区桃浦科技智慧城内，其圆锥形山体高度H=9.5 m，坡度1：3，底部宽度（2r0）为57 m，填土重度γ=20 kN·m-3，最大荷载p0=γH=190 kPa，场地地下水位埋深1 m，场地土层参数见表2。由式（6）计算山体中心点竖向附加应力，然后采用分层总和法计算荷载中心地表沉降，总沉降量s为各分层压缩量之和，即

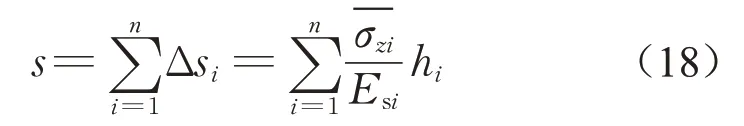
压缩层厚度取附加应力为自重应力的10%所对应的深度［14］，计算得到的压缩层厚度为41.6 m，大约为荷载底部宽度的0.75 倍。各土层压缩量见表2，总沉降量为701 mm，与现场监测得到的总沉降806 mm 较为接近。现场除了固结沉降以外还包括施工期间的瞬时沉降，因此实测沉降略大。

如果采用p0=190 kPa、2r0=57 m的三角形条形荷载来计算，计算得到压缩层厚度为63 m，大约为荷载底部宽度的1.1 倍。计算得到的总沉降量为1 027 mm。可见，这种方法会明显高估压缩层厚度和地基沉降量。

4.2 山体相互影响算例分析

下面通过一个算例来定量分析山体荷载作用下的地基沉降以及相邻山体之间的相互影响。图7所示的圆锥形人造山体A和山体B，半径r分别为36 m和18 m，高度h分别为12 m和6 m，山体填土重度取20 kN·m-3，这样最大荷载p0分别为 240 kPa 和 120 kPa。地下水位埋深1 m，地基土分为两层，浅层为软土（厚度为H1），深层为砂土，地层参数见图7。软土层厚度H1分为两种情况：H1=20 m 和H1=50 m，分别代表一般厚度和深厚软土层。分析图7所示两山体中心点（O1、O2）和角点（O3）三个位置在两种地层条件下的地表沉降。对于每种地层情况，均分别计算以下三种荷载情形下的沉降：①山体A 单独作用；②山体B单独作用；③山体A、B共同作用。

表2 某堆山工程计算结果对比Tab.2 Comparison of calculation results of a mountain piling project

地表沉降计算采用式（18）所示的分层总和法。以山体B 中心点O2为例说明附加应力的确定。在分析自身山体单独作用下的沉降时，竖向附加应力系数采用式（7）计算；在分析山体A对其沉降影响时，竖向附加应力系数采用图4给出的曲线；在考虑山体A、B共同作用下的附加应力为二者的叠加。

图7 山体及地层示意图Fig.7 Schematic diagram of mountain and stratum

三个位置处地表沉降的计算结果如表3 所示。表3中比例的含义是某计算点正上方山体单独作用下产生的沉降与两山体共同作用下产生的沉降的比值。

如表2所示，在H1=20 m的情况下，山体A单独作用下O1点沉降1 590 mm，山体A、B共同作用时沉降并未发生变化；山体B 单独作用下O2点沉降545 mm，山体A、B 共同作用时沉降561 mm。总体上讲，锥形山体相互影响下的中心点沉降增加并不显著，这与前面的竖向附加应力分析给出的结论是一致的。但是，角点O3沉降相互影响较为显著。另外，两个山体单独作用下，角点（点O3）沉降仅为中心点（点O1和点O2）沉降的10%左右，表明中心点和角点的差异沉降较大。

在H1=50 m 的情况下，由于黏土层厚度的增大，总沉降值增大，且两山体相互影响的程度略增大。由于山体A作用，山体B中点O2的沉降增加值占总沉降的比例增加到6.9%。表明地质条件会在一定程度上影响山体之间的相互影响，黏土层厚度大的情况下的相互影响更为显著。