基于浮动车数据的城市区域路网关键路段识别

赵建东，贾卓瑾，梁营力，孟畅畅

(1.北京交通大学 a.交通运输学院，b.综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044；2.河南省交通规划设计研究院股份有限公司，郑州 450000)

路网节点和路段连通范围的不断扩大，导致路网极易受到随机变化的交通状况的影响，随着时间蔓延就会产生更严重的大面积路网拥堵或是瘫痪.研究中由于关键路网对路网的正常运行起着决定性作用.因此,如何快速有效识别关键路段就成为交通管理和出行路径选择的重要研究方向.

当前，识别关键路段的方法按照度量角度主要分为直接度量和间接度量两类.

直接度量法可采用网络理论知识，直接比较路段的关键程度，也可通过统计各路段和交叉口交通流量在突发事件产生后的变化情况直观反映出各路段对道路网的影响程度.王正武等[1]将网络单元中断后的受阻塞程度用作评估各组成单元重要性的指标，田钊[2]提出了基于路段静默度和路段拥堵时间分布的中央路段检测方法，分别考虑实时的流量、速度、交通状态和占有率四个特征指标建立交通状态模型识别网络中的关键链接.

对于间接度量，Scott等[3]提出了采用网络鲁棒性指数，通过建立无约束的用户均衡模型来计算路网的鲁棒值，以此作为衡量路段关键程度的指标.Sullivan等[4]提出了一种识别路网中的路段运输脆弱性的方法，利用不同路段的容量中断值，来识别和排序道路交通网络中关键的路段.

国内研究中，王伟等[5-6]都是考虑了道路故障的可能性和失败的后果来进行识别.苏飞等[7]考虑路段的时空相关性时，分析了每个路段与相邻路段之间相对于交通流量和不同时滞的空间关系相连程度来定义路段重要性大小.王琳璨[8]选择了空间核度值、节点度和饱和度估计定为评估指标，从风险因素的角度计算交通故障概率和收益权重作为判定依据.李彦瑾等[9]根据排队能力测量路网总阻抗的变化情况，通过负载平衡确定阻抗，创建了网络流量受容量约束的模型.刘文文[10]构建了局部和全局特征的评价指标体系来对关键路段进行评价.张喜平[11]提出了一种基于场论的复杂路网中路段重要性的评估函数模型进行重要性判定.

直接度量的相关指标是可以反映出道路实际交通状况的数据，但对于数据量大的交通流，计算效率低，受影响因素众多，误判可能性较大.因此近年来，对于关键路段的识别趋向于采取间接度量的方法，其中路段的可靠性程度结合其他指标能够综合评判路段的自身属性与实际路网的特性，使得结果更符合需求，但是文献中的识别方法大多未考虑到路段通行能力随机变化的特征.因此，本文作者基于机动车GPS数据，拟采用间接度量方法结合蒙特卡罗法(Monte Carlo，MC)开展城市区域路网关键路段识别研究与分析.

1 浮动车数据处理

1.1 浮动车数据来源

原始数据来源于北京市2018年4月15日至4月28日机动车GPS数据，每条记录共有9个字段，包括检测日期、车辆经纬度、方向角、定位时间等.每辆车每隔5 s进行一次车辆GPS数据的记录.

1.2 异常数据处理

针对原始数据中的5种异常数据，分别提出相应的处理方式，对应的处理流程如图1所示.

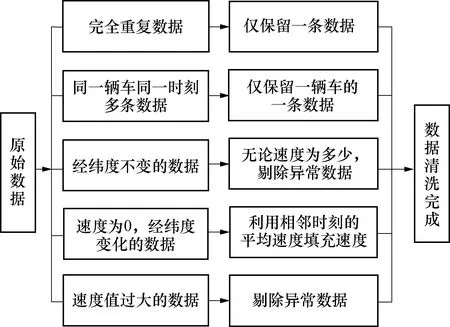
图1 异常数据处理流程图Fig.1 Flow chart of processing abnormal data

1.3 地图匹配

运用Python和MapInfo程序对清洗完的数据进行地图匹配处理：将数据中的经纬度与实际地图对比后，进行坐标转换，剔除掉偏离实际路网的数据.地图匹配后的数据反映在MapInfo中可以看出每条路段上流量的总体分布大小.

2 模型建立

2.1 关键路段识别流程

根据城市道路网关键路段识别流程图，如图2所示.确定路网的脆弱路段单元，即事故发生后最有可能被破坏的道路网络的组成部分；之后确定路网的重要路段单元，即在受损后会对路网的服务能力产生最大影响的路网组成部分；基于两种路段单元分别设计出路段失效概率计算模型——用来求解脆弱路段，以及重要路段识别模型；最后，根据实际的道路网络图和关键路段识别模型筛选脆弱路段和重要路段的交集，得到最终的关键路段集.

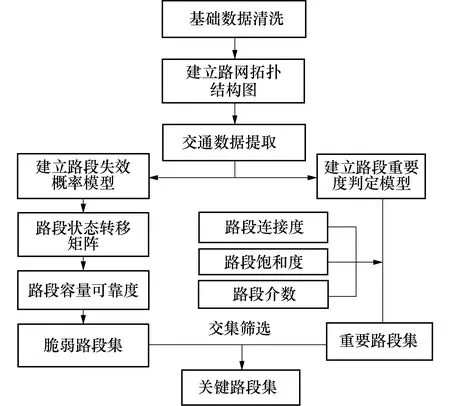
图2 路网关键路段识别流程图Fig.2 Flow chart of identifying key road sections in road network

其中重要路段判定模型需要抽象拓扑路网结构，计算各路段连接度、饱和度和介数值，进而得到路段重要度值后进行排序.路段失效概率计算模型基于正态分布的理论，结合特定的交通状况，采用随机过程(Metropolis-Hastings,M-H)进行模拟试验，代入到脆弱路段识别模型中计算容量可靠度，识别脆弱路段.

2.2 重要路段识别模型

路段重要度选取路段连接度、路段饱和度和路段介数三个指标，路段连接度的值由该条路段上起始点与终点的连接度值和路段权重决定.通常情况下，路段权重是由路段的道路等级确定，则路段a的重要度值计算可表示为

Pa=ω1×(Ma+Ba)+ω2×Ka

(1)

式中：Ma为路段连接度；Ba代表路段介数的拓扑值；Ka代表路段饱和度；ω1表示路段连接度和路段介数两个指标对于路段重要度计算的影响程度，即所占权重，ω2表示路段饱和度在重要度值中所占比重，且ω1+ω2=1.

2.3 脆弱路段识别模型

2.3.1 建立模型

考虑到容量可靠性可以全面评估整个系统的道路网络流量性能，在参数中明确考虑了道路网络中的随机因素，所以选用容量可靠度作为识别脆弱路段单元的目标.M-H可通过概率分布和原始密度样本的概率分布来描述给定的随机变化的性质，符合路段上交通流量随机变化的情况，利用改进的M-H采样，则随机性质下的采样方式可表示为

(2)

式中:π(i)为状态i的平稳分布;Q(j,i)为状态i到状态j的状态转移矩阵.

根据参考文献[12]，路段a在需求水平Da时的容量可靠度定义为

Ra(Da)=Pa(μ≥Da)

(3)

式中：μ为路段通行能力，当路段a上没有交通量，需求水平Da=0时，路段容量可靠度为1；当交通需求很大，交通量趋于无限大时，容量可靠度为0.

可假定交通需求水平为关于路段出行成本的某种函数，当达到一定的服务水平时，才能确定路段最大容量.如果设定路段的容量是随机变量，则对应的路段可靠度约束即为概率约束，对行程时间可靠度表示为

P{Ta≥φata0}≤γa

(4)

对式(4)进行改进，得到了可变的路段容量可靠度表示为

(5)

式中：φa表示路段a的失效概率；ta0为道路段a所用的最短时间;γa表示通过路段a的时间超过可接受行程时间的概率；Ta表示通过路段a的行程时间，s，根据BPR函数确定；Ca表示路段a的通过能力，pcu/h；α、β表示模型参数，通常α取0.15，β取4.0.

依据所得到的数据样本特点及目标需求，假定Ca分布函数己知，则可以对式(5)所代表的的概率约束进行显示化[13]处理，得到的常规约束表示为

(6)

2.3.2 求解算法

从已知的流量数据中可计算出V/C值，作为划分路段失效状况的依据，根据V/C数值和0.6、0.9比较大小的结果，把路段通行状况的特征划分为通行自由、通行通畅以及通行已失效3个稳定状态，还有三种状态之间的9个相互转移的过程状态，三种状态之间的转移是无向的，各个状态均是联通的，没有孤立点.图3是关于路网交通状态转移矩阵的示例，各个状态之间转移的概率由历史数据的先验分布处理分析后得到，其中V/C值的结果收敛后大于0.9的路段状态设定为路段失效,得到的概率值为路段失效概率.代入到模型中进一步求解容量可靠度判定路段脆弱性.

图3 路网交通的状态转移矩阵示例Fig.3 Sample state transfer matrix in road network

将路段失效概率代入到基于容量可靠度的路段脆弱性判定模型的式(6)中，利用式(2)中M-H采样方式创建符合路段上交通流量随机分布的采样范围，作为进行大量的随机性模拟试验的基础，对模拟实验结果统计分析，即可得到各路段的容量可靠度.

计算时，设定了如下假设：路段实际通行能力的范围，即随机序列的产生范围由历史数据确定，产生突发事件的概率均包含于历史分布中，不考虑发生额外突发事件的状况，并需先确定各路段交通量的最大乘子值的上界，即各路段通行能力处于最大值时路段交通量的最大乘子值[14].

根据参考文献[15]，定义cak表示路段a在某种状况下的实际通行能力，则路段a实际通行能力Ca的分布律表示为

P{Ca=cak}=pak

k=0,1,2,…,Ha-1

(7)

s.t.

(8)

式中:pak表示路段a实现这种通行能力的概率；Ha-1表示路段a在实际路网中的随机状况.

2.4 关键路段识别模型

综合考虑失效概率和失效后果建立重要路段识别模型和基于容量可靠度的脆弱路段判定模型，建立关键路段的识别模型，具体的计算过程如下：

步骤1 用重要度值来量化路段失效后产生的影响，识别路网重要路段；

步骤2 计算路段容量可靠度，将路段脆弱性量化表示，识别路网脆弱路段；

步骤3 根据步骤1和步骤2中得出的重要路段集和脆弱路段集，计算路段集交集实现对关键路段的识别，对路段集的交集计算表示为

I(a)=η(a)×Q(a)=

[1-λ(a)]×[1-p(a)]

(9)

式中:Q(a)表示路段的失效概率，来自于脆弱路段的容量可靠度的结果p(a)；η(a)表示路段的重要度结果，根据重要路段的求解结果重要度值λ(a)得到.

3 实例分析

3.1 确定研究区域

选择海淀区内具有快速路、主干路、次干路以及支路围成的复杂的城市道路网络作为研究对象，图4为验证模型所选取的实际研究路网.

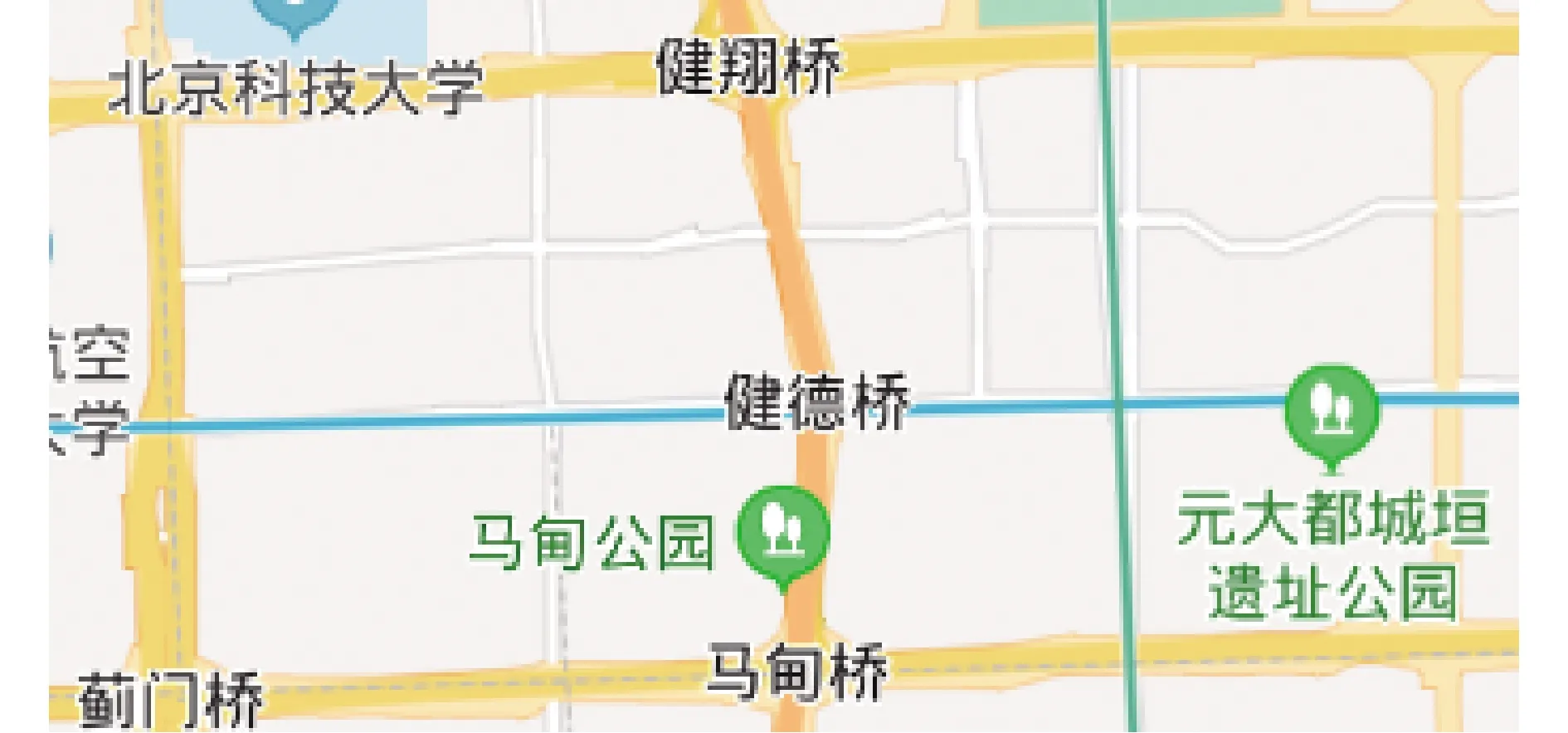
图4 研究区域实际路网图Fig.4 Actual graph of study area

3.2 数据提取

采用原始法构建路网结构，使其够体现路网实际状况与地理分布等特点，图5为利用原始法对实际路网进行拓扑得到的路网结构图.

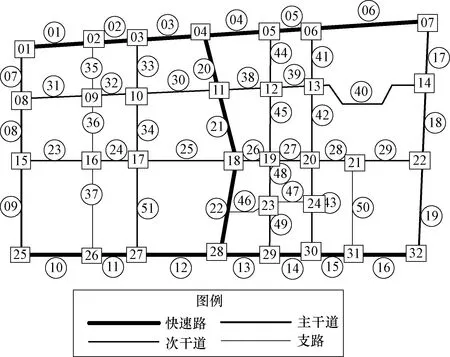
图5 实验区域拓扑结构图Fig.5 Topological structure of study area

根据路网拓扑结构图，路网中的道路被路段节点划分成多条路段，对路网上的路段进行编号，部分路段编号与所对应的路段名称见表1.

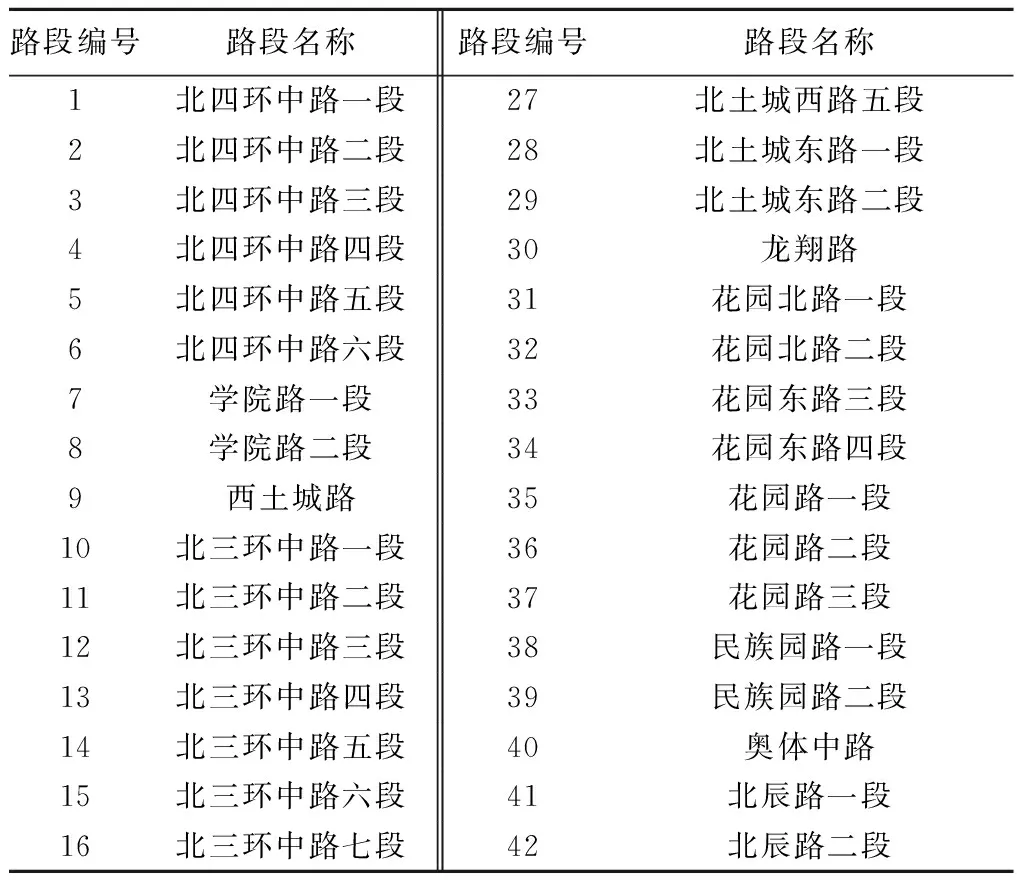
表1 部分实验区域路段编号及名称Tab.1 Section number and name of part of experimental area

实际路网中有快速路3条，城市主干道2条，城市次干道6条，支路9条，但是被路段节点划分出的路段共有51个路段单元.研究区域内路网中的每条道路按小时统计的交通流量数据统计如图6所示.

利用图6以及从其他时间分别得到的各路段交通流量数据分析，在工作日，各路段上的交通流量随时间变化趋势相同，8:00—11:00和19:00—21:00是交通流量的高峰期；在非工作日，各时段的交通流量没有很明显的区别，随时间分布较为均衡，10:00—12:00之间会出现一个出行的小高峰.

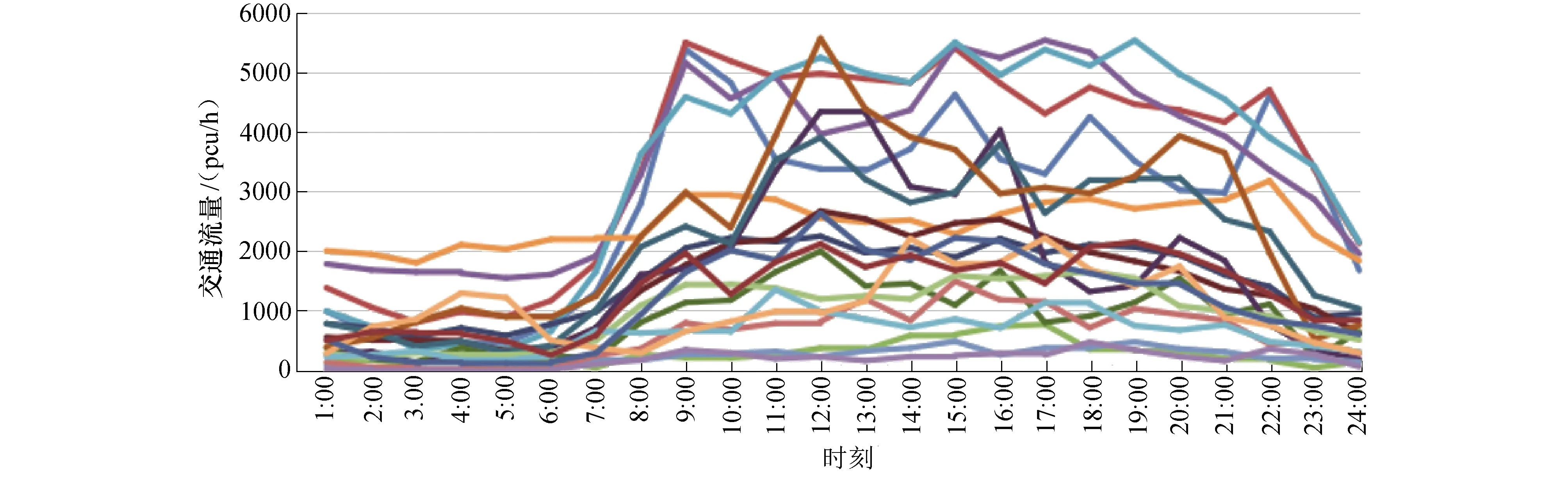
图6 实验区域2018年4月15日流量图Fig.6 Traffic flow chart on April 15th, 2018

3.3 识别关键路段

根据识别关键路段的流程图，识别该研究区域路网的关键路段分为以下三步：

1)识别脆弱路段.

根据收集到的各路段不同时间的流量数据，利用式(7)和式(8)中采用的马尔科夫链计算各条路段的状态转移矩阵，经过大量的模拟实验，将路段各状态之间转移概率收敛到固定值；之后根据式(6)中采用的M-H采样随机生成路段通行能力的分布，在路段流量范围内进行采样，计算得到研究区域内所有路段的容量可靠度结果，路段的容量可靠度计算结果如图7所示.

图7 M-H采样后各路段容量可靠度Fig.7 Capacity reliability of road sections after M-H sampling

2)计算重要路段值.

考虑每条路段的首尾节点连接段值，并且结合路段等级来计算研究区域路网中各路段单元的连接度值，部分路段的连接度值结果见表2.

将表2中得到的连接段值与研究区域路网中各条路段的介数值、高峰时期的路段饱和度值带入式(1)来计算各路段单元的重要度值，图8为该研究区域路网中各个路段单元的重要度值与路网平均重要度值的对比结果.

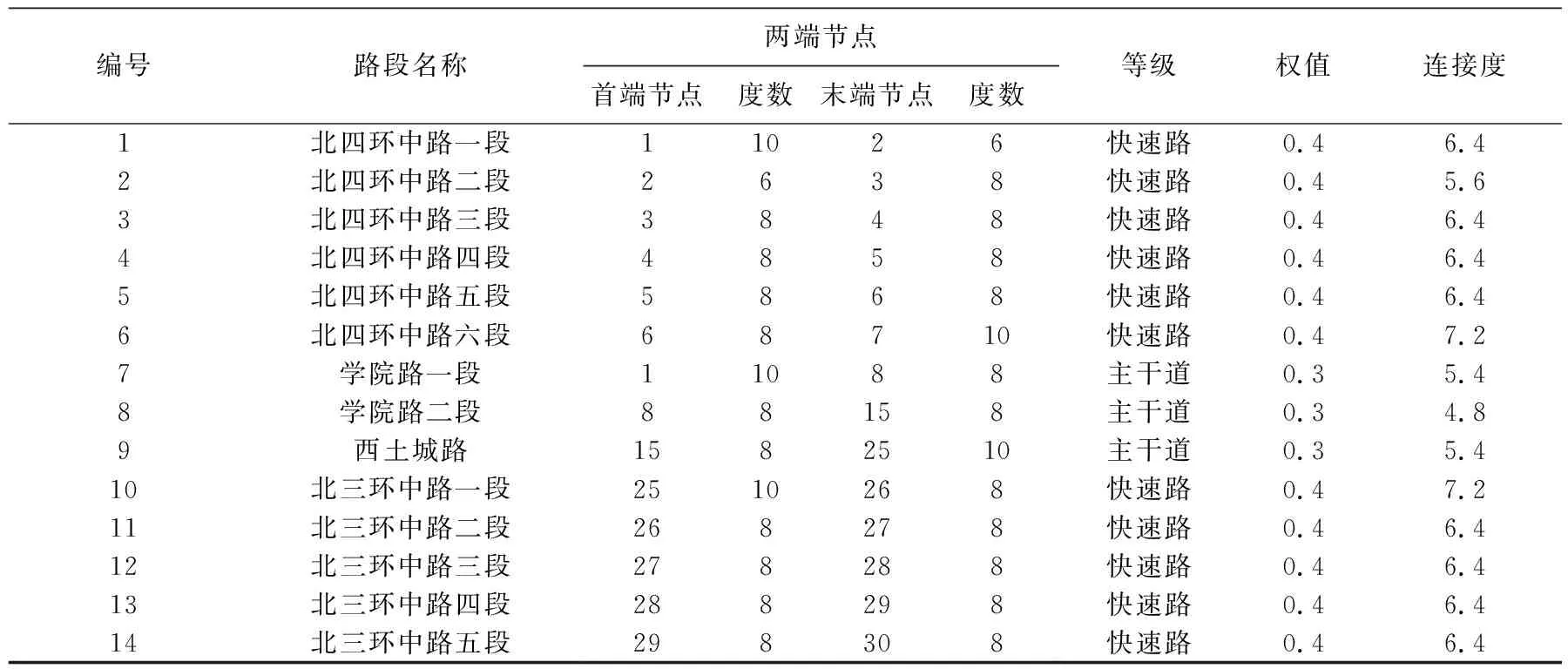
表2 部分路段连接度Tab.2 Link connectivity of part sections

由图8中可直观看出该研究区域内一些路段单元重要度值明显高于平均值，即在路网中承担作用更多，对路网影响程度较大，例如编号为20～22的路段，图中可以直观发现其重要度值很高，在实际路网中，该路段所处道路的道路等级为快速路，确实承担着很重要的通行任务，因而该计算结果符合实际路网特征.

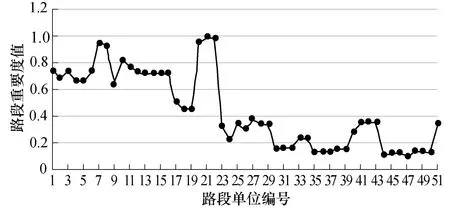
图8 路段单元重要度与路段平均重要度对比图Fig.8 Section unit importance vs. average section importance

3)识别关键路段.

研究区域的路网中一些路段单元的饱和度波动范围较大，对路段通行状况的反映更具有说服力，因此依据文献[8]中的方法，选取路段重要度权重ω1取值为0.4，路段饱和度权重ω2取值0.6.接着利用式(11)计算各路段单元的关键度值，进而识别出关键路段集.区域路网中各路段单元的关键度值结果与各自的重要度值、失效概率和容量可靠度相比较的结果如图9.

对于图9中的某些路段单元来说，例如编号为9的路段单元，根据其抽象的拓扑结构可看出该单元有较高的连通度，然而由于该路段等级较低，所以路段权值较小，该路段单元所承担运行的交通量较小，其重要度值就不高，而且失效概率低，所以路段容量可靠度就会高，那么在这种情况下就不能判定为关键路段.而有些路段单元，如编号为10 的路段单元，道路等级虽然低，但是作为连接高等级道路的必经之路，区位优势使其需要承载的交通量就较大，表现出来的容量可靠度会低，关键程度就会大.因此，路段重要度的排序和基于路段容量可靠性的路段脆弱性排序没有直接联系，对路网影响度大且重要度数值大的路段不一定是容易失效的路段，而且失效概率大的路段也不一定是重要路段.

而对于编号为20、21和22的路段，是属于京藏高速的一部分路段，路段等级高，重要度值大，交通流量大，路段易失效，是路网中典型的已经成熟的关键路段，这种类型的关键路段需要进行有针对性的改造，以降低路段失效概率，进而达到提高路网畅通性的目的.

4 结论

建立了重要路段识别模型和路段脆弱性判别模型，并利用MC求解算法识别关键路段，根据实证分析结果，得到结论：

1)路段重要度的排序和基于路段容量可靠性的路段脆弱性排序没有直接联系，对路网影响度大且重要度数值大的路段不一定是容易失效的路段，而且失效概率大的路段也不一定是重要路段.因此在规划阶段尽量避免既重要又脆弱路段，侧重承担大量交通流的重要路段,要提高其面对突发状况的稳定性.脆弱路段要重点防护通畅性，避免承担过量交通流.

2)从识别模型研究发现，因为路段重要度数值能够反映出单个路段对于整个路网运行效能的影响程度大小，更具客观性；而基于容量可靠度的路段脆弱性概率指标是从道路用户角度出发的，自身的出行计划和出行目标是最大的影响因素，更具主观性.因此，关于路段脆弱性判定模型中概率指标所占的权重小于判定路段重要度的指标数值所占权重.

3)对路网中关键路段的结果分析，快速路和主干道道路等级高，关键程度高于其他道路，区域中尤其是属于京藏高速的一部分路段，交通流量大，容易失效.而对于已经成熟的关键路段，需要进行有针对的改造，提高其可承担的交通流量阈值或者减少路段上的流量，以降低路段失效概率.

4)解决关键路段遇到的通行失效问题还可通过对其他路段进行改造，提高其通行能力，来替代路径分流关键路段上的交通压力，这对保障路网畅通具有重要意义.