湿模态特征下张力腿结构传感器布点优化
2020-07-29刘城,常进云,王世圣,郭杏林,武文华*
刘 城, 常 进 云, 王 世 圣, 郭 杏 林, 武 文 华*
( 1.大连理工大学 工业装备结构分析国家重点实验室, 辽宁 大连 116024;2.中海石油(中国)有限公司 北京研究中心, 北京 100027 )
0 引 言
TLP是一种广泛应用于深海的浮式平台,由于采取一组张紧钢管系泊[1],故又称为张力腿平台.作为TLP的重要组成部分之一,张力腿在位时的工作状态受到操作条件、海洋环境条件和浮体运动等影响[1].海洋环境条件的非平稳随机特征及其时变特征,及张力腿与平台浮体相互作用的耦合性和非线性等,使设计工况的海洋荷载模型无法准确反映作用在张力腿上的真实荷载和实际响应,增加了张力腿在位安全的不确定性.一旦张力腿结构在现场作业中出现故障,将影响整个平台的生产和安全.
结构健康监测系统通过实时获取环境荷载和结构响应的监测数据,能较为准确地评价大型装备在真实荷载条件下的结构运动状态和力学行为[2],已获得广泛的关注和足够的重视.但是由于海洋环境存在很大的未知性和复杂性,海水的腐蚀、海生物的附着都会缩短监测传感器的正常使用寿命,影响整个系统的长期可靠性;同时传感器的水下安装、维护和更换成本昂贵也给水下结构的健康监测带来了不便,合理有效地在结构上布置传感器,尤其是张力腿等大长细比水下结构的传感器优化布设,对于提高监测信息采集效率,减少传感器安装的数量和维护费用有重要意义[3].
TLP张力腿监测主要分为张力状态监测和运动响应监测,由于张力腿结构在安装过程中已有专门的顶张力监测设备,文中主要讨论流致振动响应的监测传感器布点优化问题.通过对张力腿位移和加速度的监测,可以直观反映出其运动状态,并可以计算出张力腿的应力和应变,及时发现张力腿在位状态下的不安全因素.
当下诸多学者针对陆上结构的传感器布点优化问题开展了多方面的研究,取得了众多研究成果[4].Kammer于1991年提出的传感器布点优化的有效独立法(EI)[5],是根据每个传感器对结构模态向量保持线性无关的贡献度来筛选布点位置[6].Imamovic于1998年对有效独立法进行了改进,称之为有效独立-驱动点残差法[7].近年来,采用遗传算法[8]、模拟退火算法[9]、猴群算法[10]等智能算法对结构进行传感器的布设优化也得到了关注和发展.有效独立法筛选速度快,并且可以使关注的模态向量在较少测点状态下保持较高的线性独立,使得在监测中可以用较少数量的传感器获取到最优的模态信息[11],因此被广泛应用于传感器的布点优化中,尤其适合于张力腿等沿轴向质量变化不敏感的大长细比结构[12].
本文考虑张力腿结构的湿模态特征,利用有效独立法开展传感器初始测点位置的优化筛选,结合模态置信度准则(MAC)和最小均方差(MSE)准则,提出适用于大长细比水下结构的传感器布设方法.以中国南海某待建TLP张力腿为例,应用所提方法给出张力腿结构的传感器布点优化方案.
1 张力腿结构湿模态特征分析
1.1 张力腿结构和数值模型
张力腿由标准件轧制钢管或高强度钢管组装而成[13],主要用于连接TLP平台与海底基座,保证平台浮体在风、浪、流的作用下有正常的定位能力和运动状态[14],为TLP提供相对稳定的海上作业环境,图1为TLP结构示意图.
图2为典型张力腿结构示意图,其中张力腿顶端与平台连接,底端插入到海底基座中形成自锁连接.在数值模拟过程中将张力腿模型底端模型化为固支,顶端模型化为简支,图3给出了某典型张力腿结构的力学仿真模型.
1.2 张力腿结构湿模态选择
模态分析是深海结构传感器布点优化的基础.通常将在空气/真空中的模态分析称之为干模态分析,湿模态分析是指考虑流体与结构之间耦合作用的模态分析.国内外一些学者在研究深海结构动态响应时,往往采用干模态分析,忽略了海水的作用,致使计算结果与实际情况有出入[15].
考虑流固耦合作用,TLP张力腿结构的动力学方程如下[16]:
(M+Mw)x″+(C+Cw)x′+(K+Kw)x=0
(1)
式中:M为质量矩阵,Mw为附加质量矩阵,C为阻尼矩阵,Cw为附加阻尼矩阵,K为刚度矩阵,Kw为附加刚度矩阵,x、x′、x″分别为振动位移、速度和加速度向量.
使用商业软件Ansys中Modal+Acoustic Extension模块进行湿模态分析.在忽略阻尼作用下,利用Workbench DM创建三维模型(如图4所示),分为固体区域和流体区域两部分.其中固体区域为空心圆管,底端和顶端分别采用固支和简支约束.根据文献[17]进行圆柱体流固耦合数值模拟计算时,圆柱体表面距离流场边界距离为20D(D为圆柱体直径)有较好的模拟结果,因此设置流体区域为直径20D的圆柱形流场,密度设置为1 025 kg/m3,声速设置为1 500 m/s.将流体模型与固体结构模型的交界面设置为流固耦合面.首先对流体区域与固体区域分别建模,再将流、固模型合成新体,防止网格划分时出现干涉情况.文中流体区域和固体区域均采用六面体网格,其中流体区域共划分88 400个网格单元,固体区域共划分4 600个网格单元,并且近壁面处网格采用加密处理.流体区域网格划分如图5所示.
2 张力腿结构布点优化方法及评价准则
2.1 有效独立法
有效独立法本质是根据每个传感器对结构模态向量保持线性无关的贡献度来筛选布点位置,利用较少的传感器得到更多的模态反应信息[18].根据模态矩阵得到信息矩阵,以每个测点对目标模态矩阵独立性所做的贡献大小排序,顺次删去对其秩贡献最少的测点,使Fisher信息矩阵得到优化[19].
定义输出响应为u,则[5,20]:
u=Φq+N
(2)
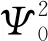


(3)

(4)
其中E表示期望值.
引入Fisher信息矩阵A:
A=ΦTΦ
(5)
将A代入式(4)可得:
(6)
(7)
首先应该求解矩阵A的特征值λ.Ψ为A的特征向量,设定传感器监测结构的各阶振型是线性无关的,则可以知道A是正定阵,那么λ为实数,可以将Ψ转化成单位正交矩阵,即有:
ΨTAΨ=λ
(8)
ΨTΨ=I
(9)
Ψ为单位正交性矩阵,所以令
G=[ΦΨ]⊗[ΦΨ]
(10)
G中每列之和为A的特征值,即测点对A的特征值贡献度可由各列元素值代表.因此可以构建各方向并重的绝对识别空间:
F=[ΦΨ]⊗[ΦΨ]λ-1
(11)
矩阵F中元素Fij表示第i个测点对第j个特征值的贡献.
分别对F矩阵各行元素求和,故有效独立向量Ed表示为
(12)
可以将Ed改写成对角矩阵E:
E=ΦΨλ-1ΨTΦT=Φ[ΦTΦ]-1ΦT
(13)
有效独立系数Eii等于或接近于0表示该传感器测点很难有效识别目标结构的模态,应该被排除;Eii等于或接近于1时测点应当被留下.有效独立法就是将有效独立系数按照大小进行排序,在所有测点中顺次删除Eii最小的点,直至获得最终的传感器布设方案.
2.2 模态置信度准则和最小均方差准则
2.2.1 模态置信度准则 根据动力学理论,海洋结构的各阶模态向量在节点上具有正交性.实际上,传感器所测的自由度少于模型本身自由度,且存在环境作用和仪器测量误差,致使所测模态向量不具备正交性,甚至会丢失关键模态[21-23].故选择海洋结构传感器安装位置时应保证所测各模态向量具有足够的空间交角,最大程度地保留原模型的动力学特性.MAC矩阵表达式如下:
(14)
其中φi、φj为第i、j阶模态振型向量.MAC矩阵非对角线元素限定在0和1之间,且数值越小模态正交性越好,模态越容易分辨.一般认为0.05为两个模态向量分辨的临界值[24].
2.2.2 最小均方差准则 首先利用有限元数值计算方法获取海洋结构湿模态振型数据;提取部分已知测点数据,使用三次样条插值方法对其进行扩展,得到一组扩展模态数据,基于均方差来评价两组测点数据,不同的传感器测点布置方案会计算出不同的均方差,选取均方差最小的作为传感器布置方案.其表达式为[25-26]
(15)
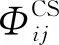
3 某典型TLP张力腿传感器优化分析
以中国南海某待建TLP张力腿为例,该TLP所处水深约404 m,平台连接8根张力腿筋腱.每根张力腿底部与海底基座形成自锁连接,顶部通过连接器与平台浮体连接,其张力腿模型参数如表1所示.

表1 张力腿结构模型参数
表2给出了张力腿前10阶干模态和湿模态的固有频率.
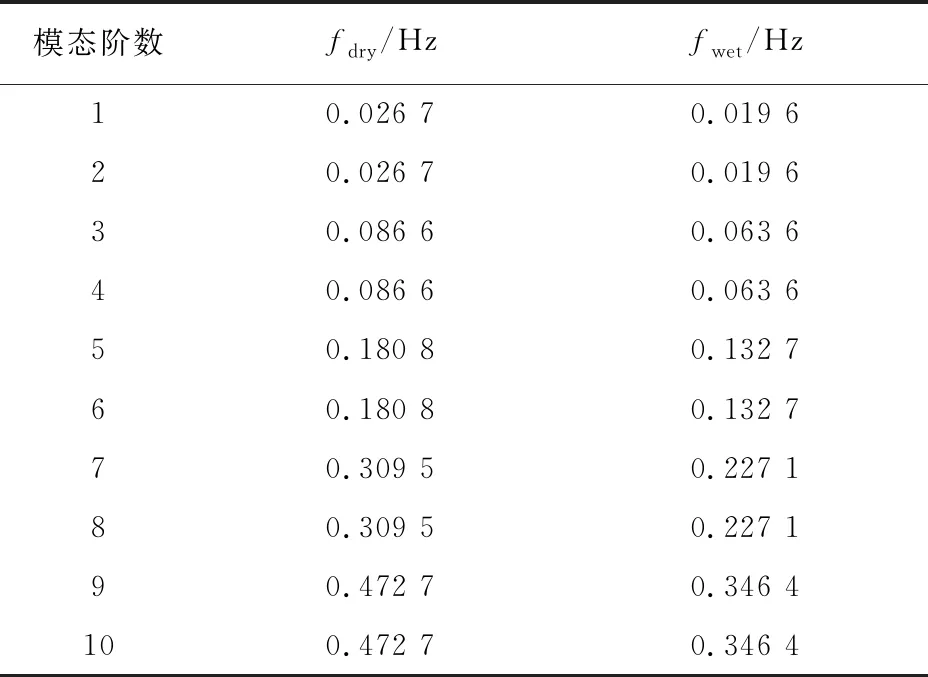
表2 张力腿模型前10阶干-湿模态结果对比
从干模态频率和湿模态频率对比可以发现,相同阶数情况下湿模态频率比干模态频率降低30%左右.第1、3、5阶湿模态的振型如图6所示.
沿张力腿轴向等间距选取101个待测点.以前10阶模态为重点研究对象[13].使用有效独立法进行张力腿测点位置的筛选.MAC矩阵非对角线元素最大值变化曲线如图7所示,横坐标为测点数目,纵坐标为MAC矩阵非对角线元素最大值.总均方差值变化曲线如图8所示,横坐标为测点数目,纵坐标为总均方差.
由图7可知当测点数目大于等于9时,MAC矩阵非对角线元素最大值满足小于0.05的标准.由图8可知当测点数目大于等于12时总均方差值保持较小,且基本不变,此时通过三次样条插值的扩展模态与原始模态对比如图9所示.
综合考虑MAC和MSE准则后,确定以下12个测点为优选测点(见表3),作为比较,表4也给出了基于干模态的测点优化位置分布.
从表3和表4的结果对比可以看出,采用湿模态特征进行布点位置筛选与采用干模态特征进行筛选得到的结果具有明显区别,其中采用湿模态特征筛选布点,立管下部布点数量较多,中部布点数量较少,顶部布点数量与干模态特征下数量相同.
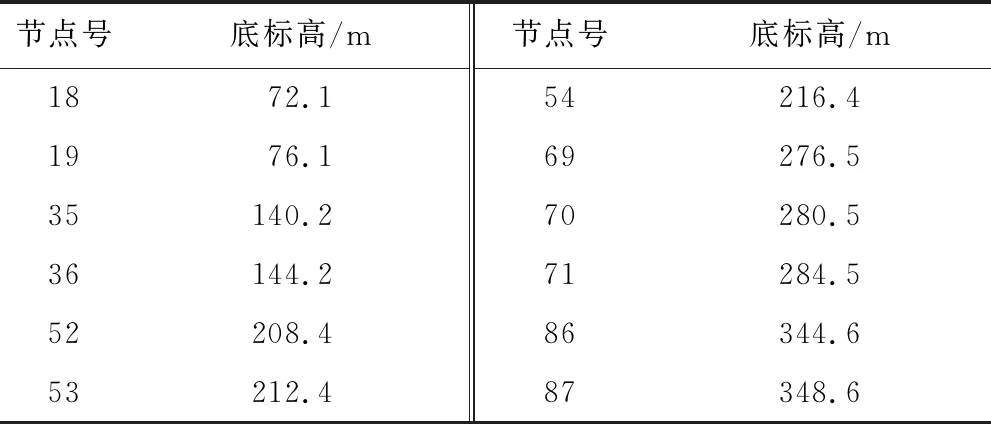
表4 干模态特征下布点位置
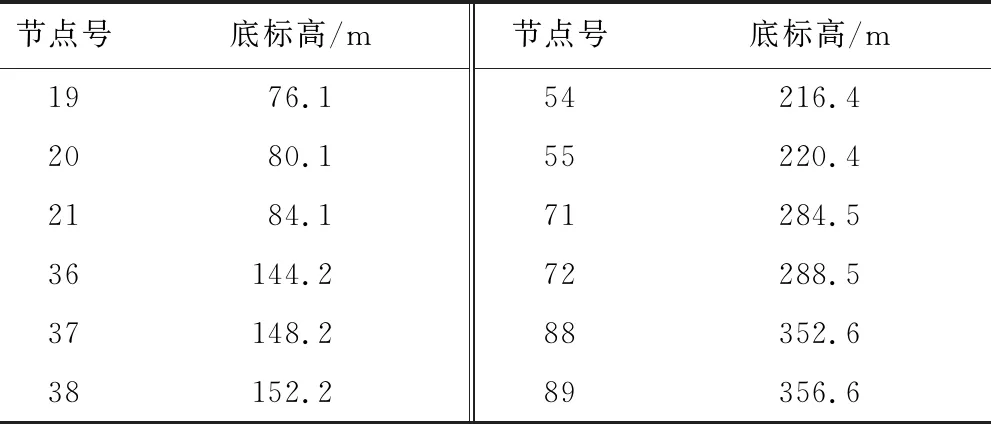
表3 湿模态特征下布点位置
湿模态特征下12个优选测点MAC矩阵值的柱状图如图10所示.
可以看出,利用有效独立法得到的测定布点优化方案的MAC矩阵非对角元素值接近于0,表明了测点间良好的独立性,显示出优化之后测点位置的合理性.
4 结 论
(1)应用Ansys中Modal+Acoustic Extension模块,考虑了张力腿结构湿模态特征,避免了只考虑干模态分析导致的与实际不符的情况.
(2)应用有效独立法对初始测点进行筛选,结合模态置信度准则和最小均方差准则逐步删除有效独立系数最小的测点,得到最终传感器测点的布置方案.
(3)以中国南海某待建TLP张力腿为例,利用EI-MAC-MSE方法进行了该实际结构的传感器测点优化分析,最终采用12个传感器的优化方案.
本文提出的基于湿模态分析方法适用于深海大长细比结构的传感器优化布点,在实际张力腿原型监测系统传感器布点优化方面具有一定应用价值,对于其他水下直立结构也具有借鉴价值.
