以形助数??化难为易
2020-07-28黎映耀
摘 要:数学为基础教育重要学科,小学数学课堂教学,使用数形结合,可实现以形助数,将复杂问题简化,实现高效教学。文章对数形结合概念和应用意义进行简要介绍,分别从讲解新知、理解概念、理解题意、解决问题等方面对其应用策略进行分析。
关键词:数形结合;小学;数学教学
中图分类号:G623.5 文献标识码:A 文章编号:2095-624X(2020)19-0031-02
数学教学中,数形结合为重要解题思想,此方法的应用和小学生数学素养的形成息息相关。应用过程中可将复杂数学问题和直观的图形相结合,让学生以清晰的思路,完成问题求解,高效学习。因此,研究此思想在教学中的具体运用意义重大。
一、数形结合概述
1.概念
从表面意义上分析,数形结合即指将数学知识、图形二者之间相关联,以图形将数学知识表达出来。小学教学,需将学生身心特点以及发展规律充分考虑,才可保证教学成效。小学生感性意识强,因此,数形结合非常适合应用在教学当中。应用过程,可将烦琐概念、复杂数据等加以转化,变为学生易于接受的方式,直观呈现知识,符合学生的身心发展规律[1]。
2.应用意义
此思想的应用可帮助学生构建完善数学体系,巩固基础,高效学习。小学生主要运用形象思维,随着年龄的增长以及阅历加深,可逐渐转化成抽象思维。数学知识抽象性特点明显,可通过图形,将抽象知识加以转化,变为形象图形,学生观察更加容易,进而对数学形成特定感知,真正走进数学世界。与此同时,在教学过程,还可以教学内容为切入点,以数形结合,指导学生掌握数学概念,明确几何问题,掌握解题技巧,形成实践能力。
二、小学数学教学数形结合的应用策略
1.讲解新知
小学生抽象思维较弱,加之数学知识逻辑性强,在新知识讲解环节,为保证学生高效学习,可将此思想应用其中。
如讲解“长方体和正方体”内容时,教学重点为让学生掌握长方体、正方体的特点。教学过程中,笔者借助多媒体设备,展示墨水盒、圆柱、长方体和正方体等图片,让学生进行观察,并提问“上述物体所有面都处于同一平面吗?”学生很容易观察出“不在同一平面”,此时,笔者顺势引导,告诉学生这些图形为“立体图形”,之后展示长方体教具,让学生触摸和观察,提问“长方体的组成结构是什么?”“面与面交点叫什么”“棱与棱交点叫什么?”等,通过实物观察和问题引导,顺利引出长方体“面”“棱”和“顶点”等知识。在上述教学过程,涉及数形结合思想的应用,可为小学生搭建桥梁,使用实物操作的方式,对图形结构展开分析,顺利过渡到新知学习当中,对原有认知进行深化,对“长方体”结构和特点等深入理解,快速找到“棱和棱”“面和面”之间的关系,对长方体“棱”和“顶点”等数量加以明确,使学生掌握长方体面位置、大小等存在的关联,提高教学成效[2]。
2.理解题意
數学教学中,线段图为常用方法之一,可直观呈现题中数量关系,辅助学生分析问题,高效解题。如讲解“分数乘法”时,涉及倍数求和这一问题,在解决这类题时,可使用线段图方式。“一件衣服原价为180元,现价比原价降低1/5,求衣服现价。”讲解此题时,笔者引导学生按照题干数量关系,画出线段图。学生画图之前,重点指导其注意线段图单位线段代表的数量为“36”,画5cm线段代表衣服原价,画1cm线段代降价钱数,之后看图解答问题。学生在直观的线段图示中,可更直观掌握已知条件之间的关系,进而列出算式180×(1-1/5)即为衣服现价。通过线段图,将数形结合巧妙融入问题讲解过程,帮助学生更直观地找到解决问题的思路,理解题干意思,进而快速解答问题。
3.解决问题
(1)几何问题。求解几何问题时,常涉及数形结合的渗透。如:讲解“正方形”相关内容时,可在问题求解环节渗透此思想。“将边长10cm的正方形,在四角内剪去边长为2cm的正方形,求出剩余图形边长。”解决此问题时,学生可能存在困惑,认为题干当中存在“剪去”和“剩余”等词语,就会走进思维误区,错误认为周长变短。对此,讲解过程,可运用此思想,将题干信息以图的形式呈现出来,并使用平移的方法,引导学生观察原图形周长和裁剪后图形的周长有怎样的关联。学生在观察过程中,可快速发现原图形和剩下图形二者周长相等,进而体会物体图形面积变小,周长可能不变。通过此案例,可以看出,数形结合在求解几何问题时,可将图形加以转化,变为规则图形,快速解出答案。通过此思想的运用,可感受到几何问题中“变”和“不变”等关系,掌握问题求解方法。
(2)寻找最值。数学中,最值问题的寻找为常见问题,在求解过程中,可运用数形结合,让学生通过图形,快速找到最大值和最小值等。如讲解“公倍数和公因数”内容时,提出问题“找出12和24的公因数,并找出最大公因数”。常规方法为,将12和24所有公因数列举出来,之后找到最大的公因数。但是,解题时间较长。对此,可在数形结合方法的应用下,指导学生使用集合图,将二者公因数以集合的形式体现出来,并让学生观察图形,可以看出,二者最大公因数即为其他公因数乘积。这种方法直观、快速,并且在此基础上,还可指导学生使用“短除法”的方式,快速求解两数最大公因数,对于学生思维的培养以及认知的形成有重要影响[3]。
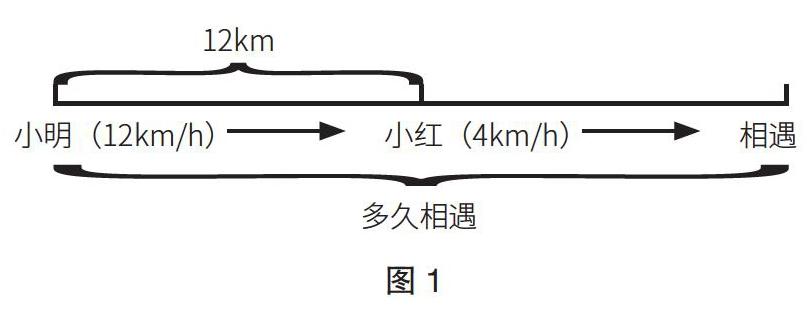
(3)追击问题。小学数学,追击问题为典型题,在解答过程中,可应用此思想,将行程图画出,顺利求解。如:小明和小红家相距12km,二人同时出发,同向而行去学校,小红步行速度为4km/h,小明骑自行车,速度为小红的3倍,求小红出发多久之后,小明和小红相遇?学生读完此题之后,由于描述内容抽象,可能出现思维混乱的问题。此题常规解决方法为:假设小红出发x小时之后,小明和她相遇,则可列出方程12x-4x=12,解得x=1.5,求解过程涉及列方程,并需要准确找到二者速度差和行驶路程之间的关系,才可顺利求解。为简化求解方式,笔者引导学生使用画图方法,将二人行驶状态描述出来,理清问题思路。图1为行程图。
通过上图,可以看出,小明和小红相遇时,比小红多行驶了12km,可以此作为解题关键点,先求解出二者的速度差,由小红步行速度4km/h可知,小明的速度为4×3=12km/h,因此,二者的速度差为8km/h,根据二者行驶的路程差,可求解出相遇时所用时间,即12÷8=1.5h。追击问题为小学数学重要题型之一,此类题型条件变化多样,并且难易程度不一,故此,为培养学生解决此类问题的能力,需要从其逻辑思维培养入手,针对题干当中信息复杂的现状,可在数形结合方法的运用下,将复杂的问题,转化为简单的图示,并将关键信息标注其中,让学生快速找到解题重点,高效解题。
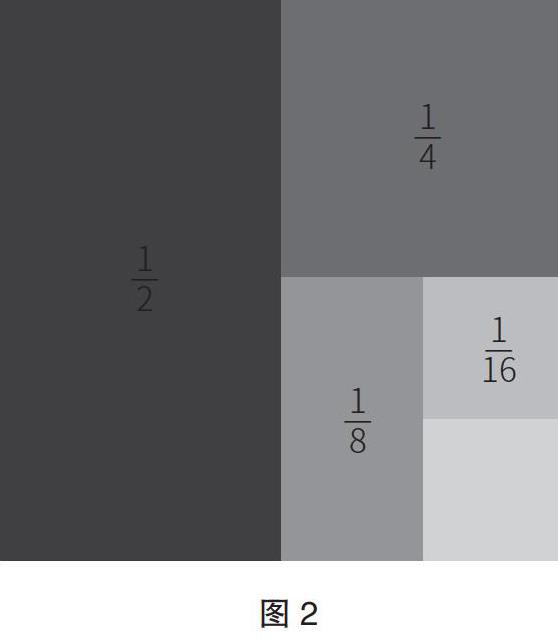
(4)复杂计算。数学教学,涉及大量的计算内容,部分计算题较为复杂,但是通过算式可找到运算规律,将问题转化成图形,在数形结合方法的运用下,高效求解。如:讲解“分数的加法和减法”这部分知识时,计算算式1/2+1/4+1/8+1/16的结果时,笔者让学生对算式展开观察,找出其特点,学生可直观看出4个加数分子全部是1,并且分母均为2的倍数,分别为2×1;2×2;2×2×2;2×2×2×2。之后提问“以怎样的方式计算较为简便?”由于学生已经具备异分母分数加减的计算基础,可想出“从左至右”的方式计算,或者“先通分,再计算”等,此时,笔者提出问题,引导学生思考“能否使用转化方式,将上述算式转化为图形,之后再计算?”并为学生出示图2。
将正方形视为单位1,并将算式内的分数依次填写到其中,思考“空白部分占据正方形整体的幾分之几?”将算式和图形之间相互联系,让学生掌握算式向图形转化的方法。学生填写过程,可以确认空白部分代表1/16,因此,正方形中涂色部分的和可以用算式1-1/16表示。此时,学生恍然大悟,原来数学计算题还可转化到图形当中,以巧妙的方式求解,并且经验证,使用数形结合方法结果为1-1/16=15/16,和常规方法1/2+1/4+1/8+1/16=8/16+4/16+2/16+1/16=15/16结果相同,但是对比求解过程,显然数形结合方法更加简便,可将复杂的计算过程化简,快速求解[4]。
总之,小学数学的课堂教学,教育者需要高度关注数形结合这一思想的应用价值,从教学内容、重点出发,找到此思想的渗透途径,帮助学生内化新知,深入理解数学概念,弄清问题含义,高效解决问题,提高教学效率。
[参考文献]
[1]吴幼山.数形结合思想在小学数学教学中的应用[J].学周刊,2020(13):141-142.
[2]潘从光.数形结合思想在小学数学教学中的实践应用[J].学周刊,2020(12):116-117.
[3]李海霞.数形结合思想在小学数学教学中的应用[J].学周刊,2020(10):107-108.
[4]张遂保.“数形结合”思想在小学中高年级数学教学中的应用[J].西部素质教育,2020(4):248.
作者简介:黎映耀(1979—),女,壮族,广西靖西人,小学高级教师,本科,研究方向:小学数学教学。
