高压下HBT 晶体的弹性性质

李 佐，张凤玲，廖大麟

（贵州工程应用技术学院理学院，贵州 毕节 551700）

含能材料的弹性性质包括弹性常数、体弹模量、杨氏模量和剪切模量等。它反映材料在常温、静荷载作用下的宏观力学性能，不但决定材料对施加应力的响应方式，还能反映含能材料的稳定性等[1]。目前，含能材料的弹性性质得到了人们的广泛关注，并对RDX[2]、TATB[3]、HMX[4]、FOX-7[5]、CL-20[6]等含能材料开展了研究。5, 5′-双四唑肼(5, 5′-Hydrazinebistetrazole，HBT)晶体是一种著名的单质富氮、高能、钝感含能材料[7]。HBT 含有83.7%的氮元素，爆炸燃烧后释放的气体主要为氮气、二氧化碳和水，因此被称为“绿色”含能材料[8-11]。本研究采用基于第一性原理的准谐振近似方法，计算固态HBT 晶体在0～120 GPa 高压下的弹性性质，同时分析其弹性的各向异性特征。

1 理论与计算方法

1.1 HBT 晶体结构优化方法

采用基于第一性原理的Quantum ESPRESSO 软件包中的PWSCF 模块[12]计算电子结构的总能量。广义梯度近似（GGA）下交换相关势采用Perdew-Burke-Ernzerhof （PBE）形式[13-14]，原子赝势平面波基组采用超软赝势加核修正的C.pbe_v1.2.uspp.F.UPF，N.pbe_v1.2.uspp.F.UPF，H.pbe_v1.2.uspp.F.UPF 形式[15]，几何优化采用BFGS 算法[16]。为增加计算精度，平面波基函数的截断能取为544 eV，布里渊空间采用Monkhorst-Pack 方法[17]，k 点方案为6 × 6 × 3，总能自洽，离子位移最大值和应力最大值都能达到设置的收敛精度。在高压下几何结构优化的基础上，利用准谐振近似方法计算HBT 晶体的弹性性质，详细的计算过程在软件Thermo_pw 中体现[18]。

1.2 弹性常数

固态物质弹性理论计算中引入应变εj（j = 1, 2, ···, 6），晶体的一个应力用σi表示。当应力较小时，σi和εj满足[19]

式中：系数Cij为弹性常数（或者弹性劲度），矩阵S 为矩阵C 的逆矩阵，Sij为弹性柔顺系数。初始构型采用Klapötke 等[7]获得的HBT 晶体的实验结构，它属于单斜结构的分子晶体，点群为C2/c 空间群，其原胞晶系属于三斜晶系，对称性最低，包含最多的矩阵元。弹性常数矩阵C 是一个对称矩阵，共有21 个独立矩阵元。计算中采用原胞结构，弹性常数矩阵表达式为

考虑到二阶弹性常数与能量满足如下关系[20]

因此，只要知道稳定构型下的晶体体积V0和能量Ec，就可以获得弹性常数。

2 结果与讨论

2.1 晶体结构参数

基于密度泛函理论的第一性原理，得到零温零压下HBT 晶体的晶格参数，如表1 所示，晶体几何结构如图1 所示。从表1 可以看出，晶格参数b、c 和V 的计算值均高于实验结果，而a 和β 却低于实验结果。在目前的第一性原理方法中，晶格参数的计算精度取决于原子赝势和计算方法的选择，因此，无法做到与实验结果完全符合。此外，采用5 GPa 间隔优化HBT 晶体在0～120 GPa 压强范围内的晶体结构。优化后获得了稳定的晶体构型，压强-体积比（p-V/V0）曲线与实验结果的比较如图2 所示。从图2 可以看出，在0～26 GPa 压强范围内，理论计算结果与Ciezak-Jenkins 等[21]的实验结果具有相同的变化趋势，并且在1 和22 GPa 处曲线相交，说明本理论计算结果与实验结果有一定的可比性。同时，给出了HBT 晶体在压强高于25 GPa 时的体积变化情况。理论计算显示，随着压强的增大，晶体体积变化受压强的影响越来越明显，60 GPa以上时压强与体积比呈线性关系。

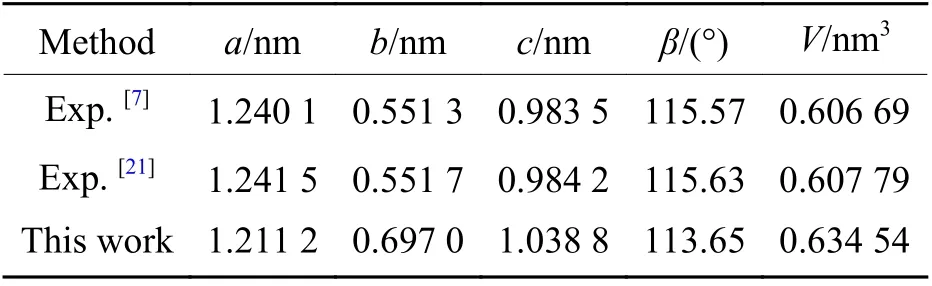
表 1 HBT 晶体晶格参数的计算值和实验值Table 1 Calculated lattice parameters of HBT crystal along with experimental data

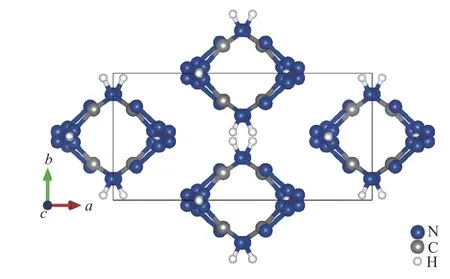
图 1 优化后的HBT 晶体几何结构Fig. 1 Geometric structure of optimized HBT crystal

图 2 理论和实验得到的压强-体积比关系Fig. 2 Pressure as a function of volume ratio V/V0 from theoretical and experimental data

2.2 高压弹性

通过高压下结构优化，得到不同压力下稳定的HBT 晶体结构，在此基础上计算弹性系数和弹性模量。三斜结构的弹性常数矩阵包含21 个独立矩阵元。Born[22]d 给出了晶体材料力学稳定性的充分必要条件为弹性常数矩阵C 正定。按照线性代数知识可知，对称矩阵C 正定的充要条件为C 的各阶顺序主子式都为正，即

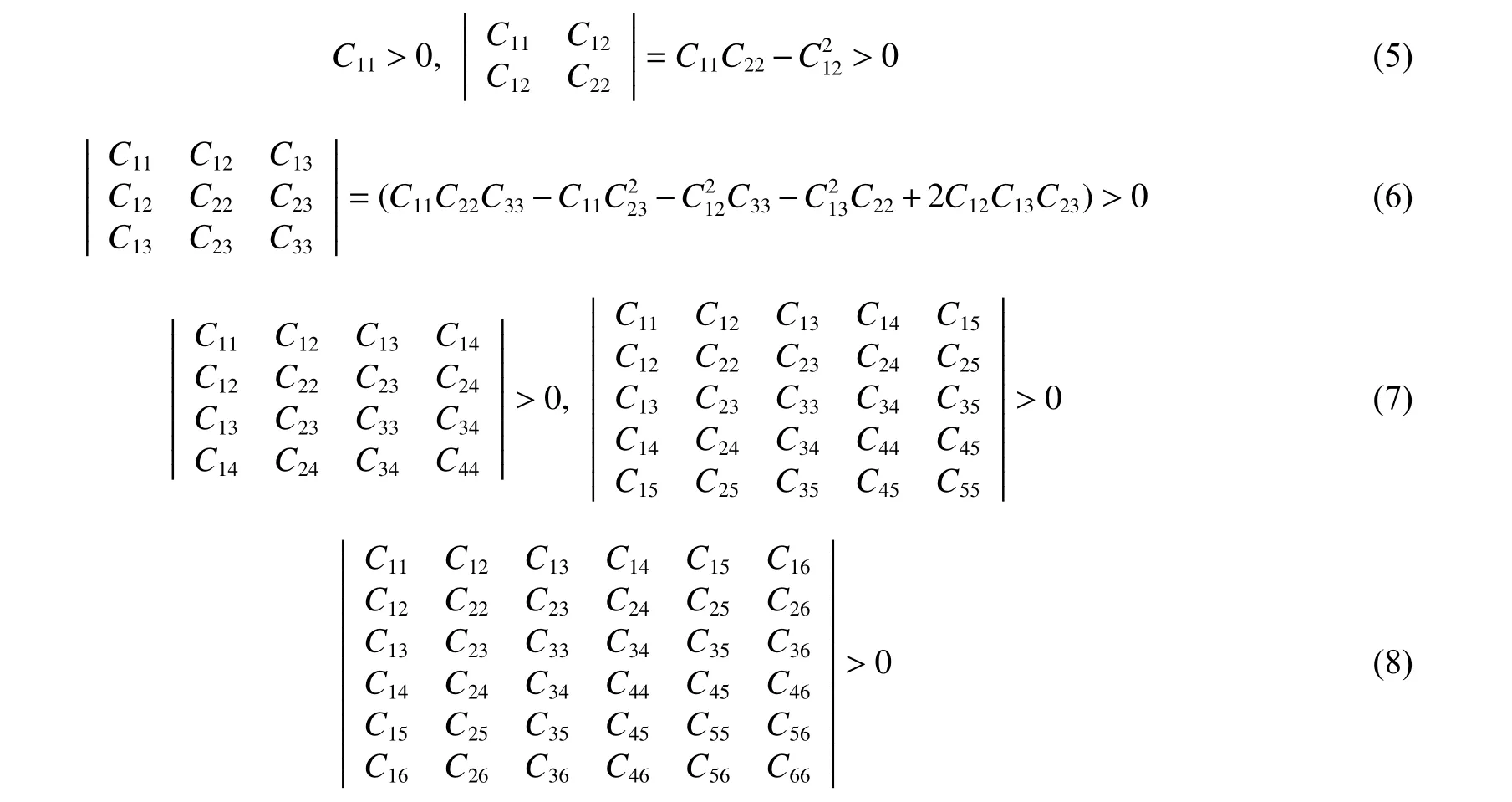
式(5)～式(8)给出了三斜晶体稳定性的充要条件。四阶以上行列式的表达式比较复杂，一般采用直接带入行列式元素来计算验证。图3(a)、 图3(b)、图3(c)、图3(d)给出了21 个弹性常数随压强的变化关系。从图3 可以看出，C15、C56、C24、C46随压强的变化比较剧烈，其中C15、C56和C24先减小后增大，而C46则先增大后减小随后又增大。将零温零压下晶体的弹性常数代入式(5)～式(8)，验证后发现符合稳定性条件。对高压下晶体进行验证，发现也符合稳定性条件，说明高压下HBT 晶体是稳定的。

计算体弹模量、剪切模量的普适公式为[23]

根据Voigt-Reuss-Hill 均值方法，有

再根据B、G 可以获得体弹模量E 和泊松比μ

依据式(9)～式(11)，可以获得体弹模量、剪切模量和杨氏模量随压强的变化关系，如图4 所示。从图4 可以看出，随着压强的增大，3 种模量的数值也增大，其中体弹模量在15 GPa 以上时表现出与压强的线性关系。而3 种模量中，杨氏模量的变化最显著，高压下的数值也最大。此外，根据Pugh[24]的理论，B/G 可作为鉴别晶体韧脆性的标准，即当B/G＜1.74 时，晶体材料表现为脆性；反之，晶体材料表现为韧性。因此，根据式(11)中泊松比 μ与B/G 的关系来计算B/G 的数值，并作出B/G 与压强的关系曲线，如图5 所示。随着压强增大，B/G 逐渐增大，与图4 的变化趋势一致。当压强低于85 GPa 时，B/G＜1.74，材料表现出脆性；而当压强高于85 GPa 时，HBT 晶体表现出韧性。类似的层状分子晶体TATB 在0～50 GPa 时表现为韧性[25]，而同为层状分子晶体的HBT 在0～85 GPa 下却表现为脆性，说明HBT 晶体对压力的响应较为敏感。

图 3 弹性常数随压强的变化Fig. 3 Variations of elastic constant with pressure

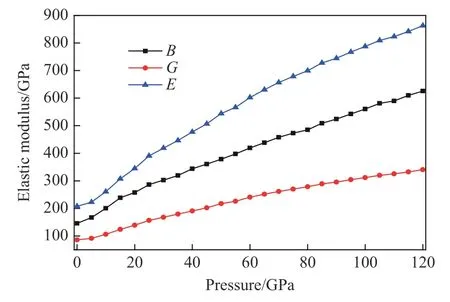
图 4 体弹、剪切和杨氏模量随压强的变化关系Fig. 4 Variations of bulk modulus B, shear modulus G and Young’s modulus E with pressure

图 5 体弹模量和剪切模量之比与压强的关系Fig. 5 Pressure dependence of the ratio of bulk modulus and shear modulus

同时，根据以下公式可以得到HBT 晶体材料的压缩波声速 vp、剪切波声速 vs及 平均声速vm

式中：h 为普朗克常数，kB为玻尔兹曼常数，n 为原子数，NA为阿伏加德罗常数，M 为相对分子质量。图6 给出了压缩波声速 vp、剪切波声速 vs、平均声速 vm和德拜温度 Θ随压强的变化关系。可见，声速随压强的增大而增大，其中压缩波声速 vp最大，且随压强变化最明显。在0 GPa 下得到的德拜温度为975 K，而120 GPa 时则为1 820 K，压强对德拜温度的影响明显。

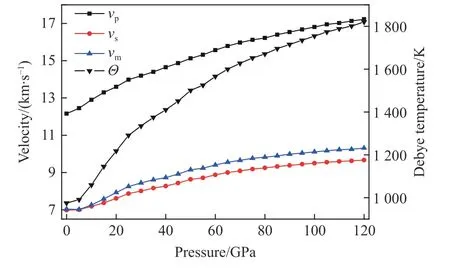
图 6 不同压强下HBT 晶体的声速和德拜温度Fig. 6 Compressional wave velocity, shear wave velocity and averaged wave velocity of HBT crystal under different pressures

2.3 高压弹性各向异性

弹性性质的各向异性是材料力学性能通常受微裂纹和晶格畸变影响的重要条件，因此，研究弹性性质的各向异性对于提高材料的力学性能有着重要的意义[27]。目前有3 种处理方案。第1 种方案是Chung 等[28]提出的体弹模量、杨氏模量和剪切模量分数比各向异性的概念，定义为

式(16)～式(18)分别用于表征材料的体弹模量、杨氏模量和剪切模量的各向异性程度。据此可以计算出模量各向异性分数比与压强的关系，如图7 所示。对于弹性各向同性材料，AB、AE和AG都为零，而AB、AG为1 表示最大可能的弹性各向异性。从图7 可以看出，AB、AE和AG均大于零而小于1，说明在0～120 GPa 的压强范围内HBT 晶体的弹性模量表现出各向异性。此外，体弹模量分数比只有很小的波动，杨氏模量和剪切模量则表现出相同的变化趋势，即先增大后逐渐减小，说明HBT 晶体在高压下的各向异性程度减弱。

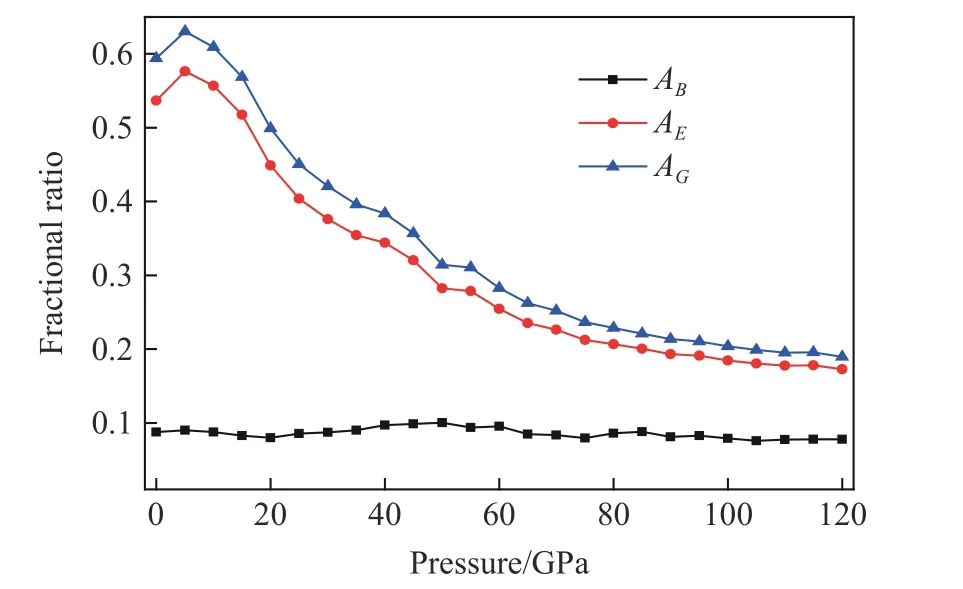
图 7 模量分数比与压强的关系Fig. 7 Pressure dependence of the fractional ratio of modulus

第2 种方案是Ranganathan 等[29]提出的全局弹性各向异性系数（AU）的概念，用来描述材料弹性模量的各向异性，具体表达式如下

图8 的纵轴表示0～120 GPa 压强范围内的全局弹性各向异性系数AU的数值，其中，最高点表示0 GPa 下的数值。从结果看都大于零，因此，HBT 晶体在高压下表现出各向异性。

此外，式(20)的AC与式(18)的AG是相等的，都是由Chung 等于1967 年提出，均用于表征剪切模量的各向异性。为了比较两种方案的关系，作AU-AC曲线。可见，两种方法都很好地描述了HBT 晶体在0～120 GPa 压强范围弹性模量的各向异性特征。随着压强的增大，AU、AC和AU/AC的数值都在减少，说明弹性模量的各向异性程度在减弱，两种方案得到的结论一致。

第3 种方案是Toher 总结和发展的Ranganathan 关于材料弹性各向异性的理论表述[30]

AL随压强的变化关系如图9 所示。可以发现，曲线的变化趋势与第1 种方案（弹性模量分数比理论）得到的结果类似，即AL先增大后减小，5 GPa 处出现转折。整体上看，高压下HBT 晶体弹性模量的各向异性程度减弱。由此可知，AC、AU和AL三者在描述HBT 晶体各向异性程度上是等价的。

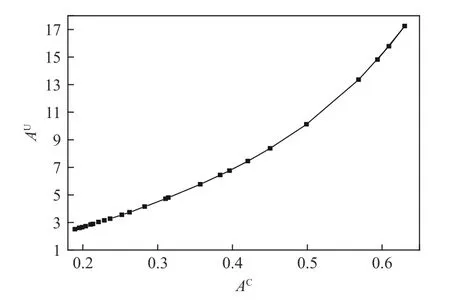
图 8 AU 和AC 的各向异性关系Fig. 8 Anisotropy diagram of the AU and AC

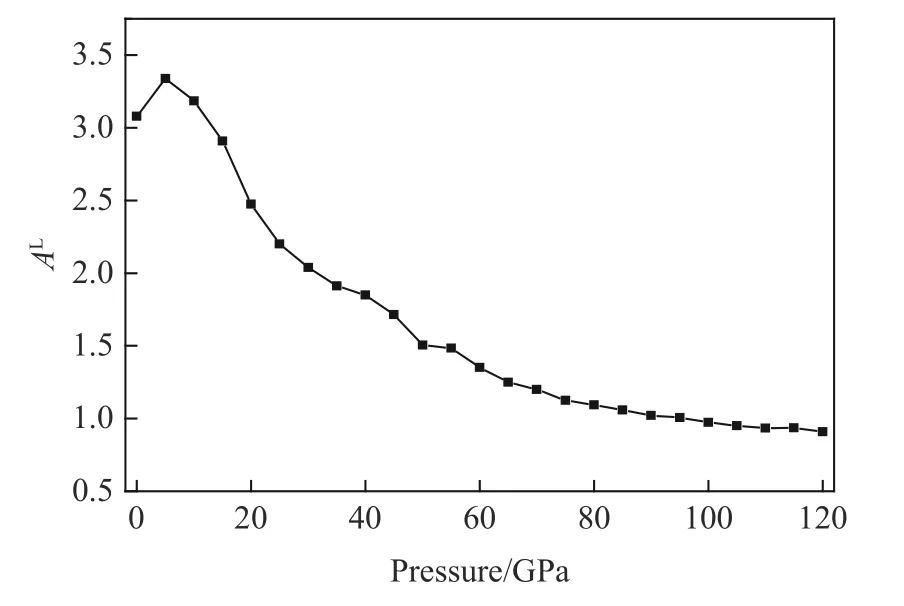
图 9 AL 随压强的变化关系Fig. 9 Pressure as a function of anisotropy index AL

从图7、图9 可以明显看出，5、25 和55 GPa 下曲线有较为明显的变化。为了进一步考察这3 个压强下HBT 晶体模量的各向异性程度，利用ELATE 开源软件[31]，将这3 个压强下的弹性系数6×6 矩阵元36 个数值全部代入，绘制出剪切模量的二维分布，如图10 所示。因单位换算，图10 中坐标轴均被放大了10 倍。图10(a)、图10(b)、图10(c)分别显示了5、25 和55 GPa 下剪切模量的二维分布。每个压强下的3 幅图分别代表剪切模量三维分布在xy、xz、yz3 个面上的投影。蓝线和绿线分别代表两个方向剪切模量的矢量投影。从图10 可以看出：压强越大，每个面上投影矢量的各向异性越强；在确定的压强下，每个面上的投影也表现出差异性。综上所述，HBT 晶体剪切模量的各向异性受压强的影响显著。

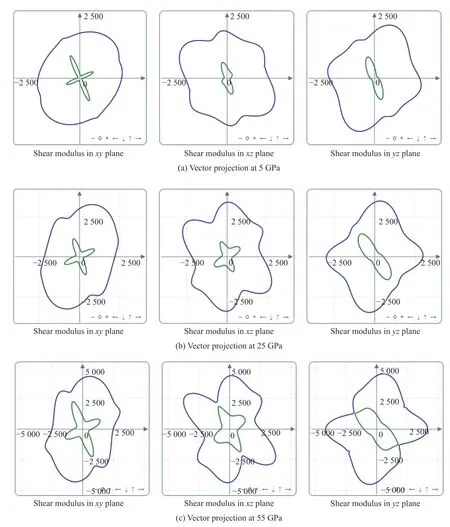
图 10 不同压强下剪切模量各向异性的二维投影Fig. 10 Anisotropic two-dimensional projection of shear modulus at different pressures

3 结 论

采用基于密度泛函理论的第一性原理方法计算了HBT 晶体在零温零压及高压下的结构，研究了高压下HBT 的力学稳定性和弹性性质，具体分析了HBT 晶体的弹性常数Cij、弹性模量（B、G、E）、声速（ vp、 vs、 vm）和德拜温度Θ 随压强的变化关系。在此基础上，基于3 种不同理论研究了弹性模量的各向异性。结果表明，弹性常数和模量都随压强的增加而增加。根据B/G 估测了HBT 晶体在高压下的韧脆性。弹性模量各向异性参量随压强表现出不同的变化规律，总体而言，高压下HBT 晶体的弹性模量各向异性程度减弱。