A Macroscopic Dynamic Constitutive Model for Ceramic Materials
2020-07-28TANGRuitaoXULiuyunWENHemingWANGZihao
TANG Ruitao, XU Liuyun, WEN Heming, WANG Zihao
(CAS Key Laboratory for Mechanical Behavior and Design of Materials,University of Science and Technology of China, Hefei 230027, Anhui, China)
Abstract: A macroscopic constitutive model is presented herein for ceramic materials subjected to dynamic loadings by closely following a previous study on concrete. The equation of state is described by a polynomial equation and the strength model takes into account various effects such as pressure hardening,Lode angle, strain rate, shear damage and tensile softening. In particular, the strength surface of ceramic materials is characterized by a new function which levels out at very high pressures and strain rate effect is taken into account by dynamic increase factor (DIF) which excludes inertial effect. The present model is verified against some available experimental data for ceramic materials in terms of pressure-volumetric response, quasi-static strength surface and strain rate effect. The model is further verified against the data for triaxial test by single element simulation approach and the test data for depth of penetration in AD99.5/RHA struck by tungsten alloy penetrators. Furthermore, comparisons are also made between numerical results of the present model and the JH-2 model. It is demonstrated that the present model can be employed to describe the mechanical behavior of ceramic materials under different loading conditions with reasonable confidence and is advantageous over the existing model.
Keywords: ceramic material;constitutive model;stain rate effect;triaxial test;JH-2 model;single element simulation approach
Ceramic materials have been increasingly used in armors, personal armor system, aeronautic engineering and vehicle engineering due to its excellent ballistic performance. An understanding of the response and failure of ceramic materials under impact loading is of great significance for the design and assessment of military hardware and protective structures.
As ballistic tests are expensive to perform and time consuming, numerical simulations have been widely employed in the design and optimization of ceramic armors. However, the accuracy of numerical simulations depends on the dynamic constitutive model for ceramic materials to a large extent. To this end, many models have been put forward[1-8]. Fahrenthold[1]proposed a continuum damage model for fracture of brittle solids under dynamic loading in which Weibull strength distribution was employed to account for the effects of flaw size distribution on the damage accumulation rate. The model was used to compute the depth of penetration in a steel plate impacted by a sphere of alumina without being applied to simulate the behavior of ceramic armors subjected to projectile impact. Rajendran[2]modeled the impact behavior of AD85 ceramic under multiaxial loading by assuming an existing distribution of micro-cracks and employing a criterion for crack growth based on theories of dynamic fracture mechanics. The strength of the intact material was rate dependent, and the inelastic deformation was modeled using an elastic-plastic cracking rule. The model predictions were found to be in good agreement with the test data obtained from plate impact tests. The most widely used constitutive model for ceramic materials in many commercial codes is the Johnson-Holmquist model (JH-2)[3]. The model employs two strength surfaces to describe the pressure-dependent compressive strength of the intact and failed materials, respectively. However, in the model strain rate effect is described by the same form of function adopted in the constitutive models for metals and concrete materials, which has been found to be inconsistent with the dynamic mechanical behavior in recent studies[9-12]. Furthermore, tensile softening cannot be accurately predicted, and no differentiation was made between the effects of strain rate and inertia (containment).
The main objective of this paper is to establish a macroscopic dynamic constitutive model for ceramic materials by closely following the previous work on concrete[9]and on the basis of the experimental observations for some ceramic materials. Various equations of the constitutive model are given and compared with some available experimental data for ceramic materials in terms of pressure-volumetric response, quasi-static strength surface and strain rate effect. Furthermore, the model is also verified against the data for triaxial test by single element simulation approach.
1 A Macroscopic Constitutive Model for Ceramics
A dynamic macroscopic constitutive model for ceramic materials is developed in the following sections based on the computational constitutive model for concrete subjected to dynamic loadings[9]with some modifications being made. There are two points which should be highlighted here, namely, (1) the pressurevolumetric response is described by polynomial equation and the phase transition (e.g. AlN ceramics) as the pressure increases to a certain value is considered; (2) a hyperbolic tangent function is employed to describe the pressure dependent shear strength surfaces of ceramic materials which level out at very high pressures.
1.1 Equation of State
Ceramics are complex granular materials, which contain a large number of micro cracks and voids just as concrete material. On the one hand, it has been observed experimentally that the volumetric strains of Al2O3and SiC increase with increasing pressure[13-16]and the equation of state for this category of ceramic materials can be expressed as polynomial equation, viz.


1.2 Strength Model

2 Verification of the Newly-Developed Constitutive Model
The present model is verified against some available experimental data in terms of pressure-volumetric response, quasi-static strength surface and strain rate effect.
Values of various parameters in equation of state can be determined by hydrostatic compression experiment and they are listed in Table 1. For Al2O3and SiC ceramic materials, the relationship between pressure and volumetric strain (Eq.(1)) can be rewritten as

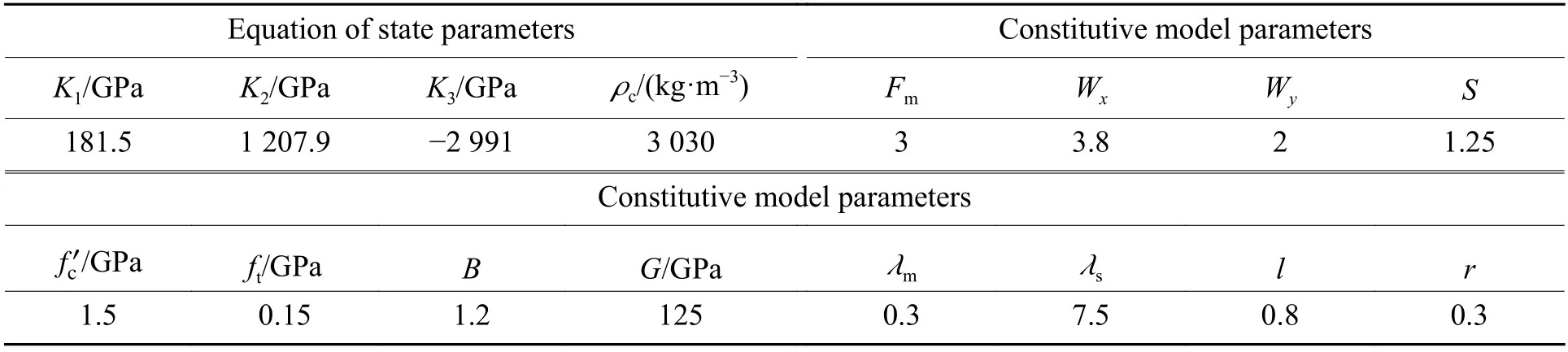
Table 1 Values of parameters for BeO in the present model
Fig.1 shows comparison of the present model predictions (Eq.(9) and Eq.(10)) with the experimental data for Al2O3and SiC[13-16]and for AlN[17-19]. It can be seen from Fig.1 that good agreement is obtained.
Fig.2(a) and Fig.2(b) show comparisons between the present model predictions (Eq.(4) with B = 1.4 for B4C and BeO and Eq.(9) with B = 1.7 for Al2O3and AlN) and the test data[25-27]for the strength surfaces.The strength surfaces of Al2O3and AlN obtained from the JH-2 model[28]are also shown in Fig.2(b). It is clear from Fig.2 that the present model predictions are in good agreement with available test results for ceramic materials. It is also clear from Fig.2(b) that the JH-2 model produces similar results to those of the present model for relatively low pressures whilst for higher pressure the present model levels out and the JH-2 model increases with increasing pressure.
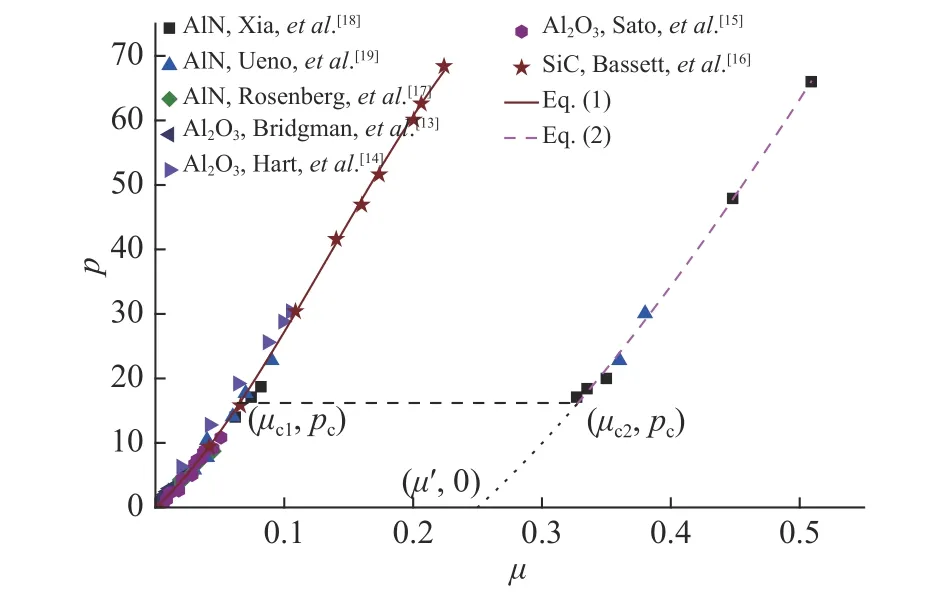
Fig. 1 Comparison between the present model predictions(Eq.(9) and Eq.(10)) and the experimental data for ceramic materials

Fig. 2 Comparisons between the present model predictions (Eq.(4) and Eq.(9)) with the experimental data
Values of parameters Fm, Wxand S in Eq.(6) for the dynamic increase factor in tension can be determined from tensile test data for ceramic materials at different strain rates. Fig.3 shows comparisons between the present model predictions (Eq.(6) with Fm= 3, Wx= 3.8 and S = 1.25) and available experimental data[29-31]for different ceramic materials at different strain rates. It is evident from Fig.3 that reasonable agreement is obtained.
Fig.4(a) and Fig.4(b) show comparisons between the theoretically predicted strength surfaces (Eq.(4))and some experimental data obtained from plate impact tests on B4C[32-34], AlN[17], Al2O3[20]and SiC[21-23]. In the calculations, a strain rate of 105s-1is taken which is of a typical value in a plate impact test. Also shown in Fig.4(b) are the predictions from the JH-2 model. It is clear from Fig.4(a) that reasonable agreement is obtained between the present model predictions and the tests results for B4C which are somehow scattered whilst good agreement is achieved between Eq.(4) and the test data for AlN,Al2O3and SiC as can be seen from Fig.4(b). It is also clear from Fig.4(b) that the JH-2 model has failed to predict the dynamic mechanical behavior of ceramic materials at higher confining pressure.

Fig. 3 Comparison between the present model predictions(Eq.(6)) with available experimental data for different ceramic materials at different strain rates (Unit of strain rate: s-1)
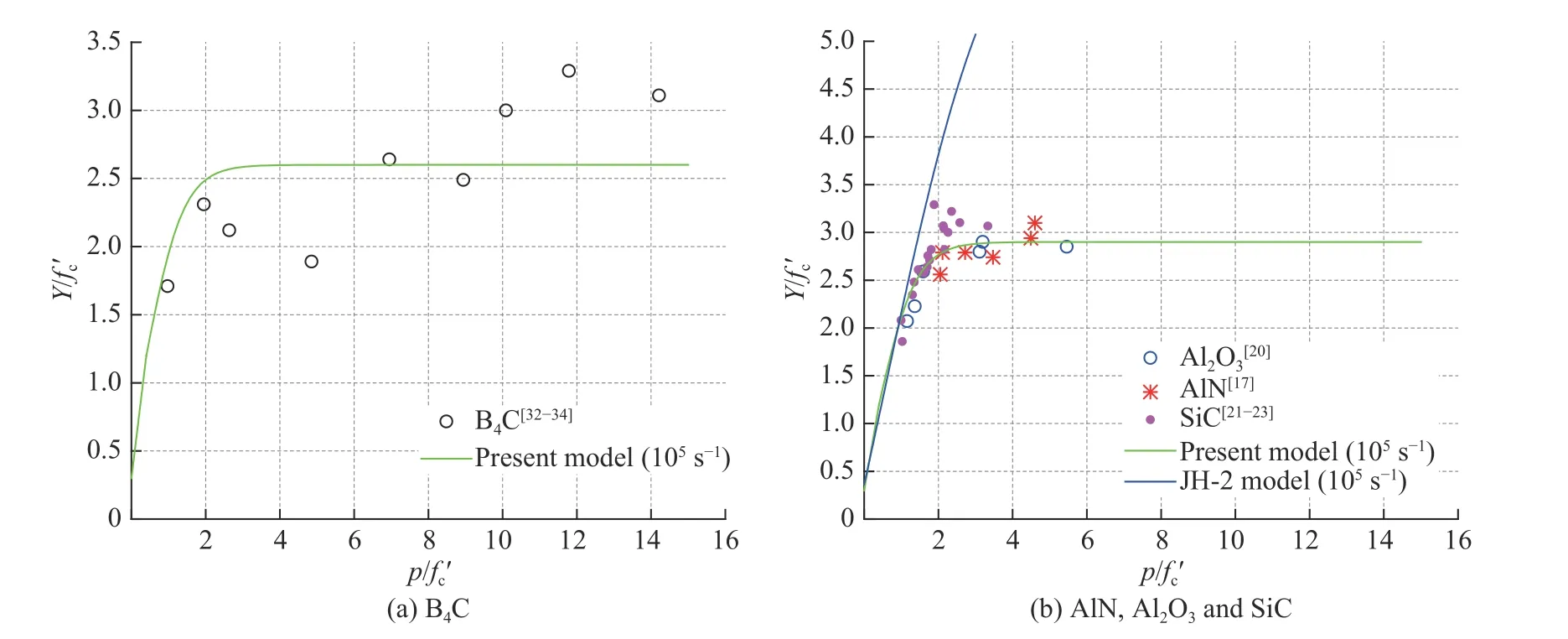
Fig. 4 Comparisons between the present model predictions (Eq.(4)) and the experimental data obtained from plate impact tests
Fig.5 shows comparison of the present model predictions and the experimental data obtained from SHPB(split Hopkinson pressure bar) tests[25]. Also shown in the figure are the predictions from the JH-2 model. In the tests, confining pressures of up to 230 MPa were applied, and a constant strain rate was employed (i.e. 500 s-1).The solid line indicates theoretically predicted quasi-static strength surface, and the broken line designates dynamic strength surface from the present model with a strain rate of 500 s-1. As can be seen from Fig.5 that a good agreement is obtained between the present model predictions and the experimental data whilst the JH-2 model underestimates the strength surface of AlN ceramic under the strain rate of 500 s-1. It should be stressed here that the present model predicts that the quasi-static and dynamic strength surfaces are parallel to each other,which has been confirmed/verified by the experimental data. It leads to further support for the accuracy and validity of the present constitutive model for ceramics.
To demonstrate the quasi-static behavior of the present constitutive model, numerical tests are performed to evaluate stress-strain relationships for ceramics under various loading conditions, which includes: (a) triaxial compression with different confining pressures, (b) uniaxial tension, (c) biaxial tension and (d) triaxial tension. The numerical tests are carried out using single element simulation approach.Table 1 lists the values of various parameters in the present constitutive model for BeO ceramic. Table 2 and Table 3 list the values of various parameters for AlN ceramic employed in the present model and JH-2 model, respectively. Parameters in the present model are clearly defined in the previous paragraphs, and in JH-2 model. K1, K2, K3are bulk moduli, and ρcis the density for ceramic material; a, b, C, m, n are strength surface parameters; pHEL, σHELand μHELare respectively the pressure, the equivalent stress and the volumetric strain at HEL (Hugoniot elastic limit); T is the maximum tensile hydrostatic pressure the material can withstand; β is strain rate parameter; d1, d2are damage parameters.
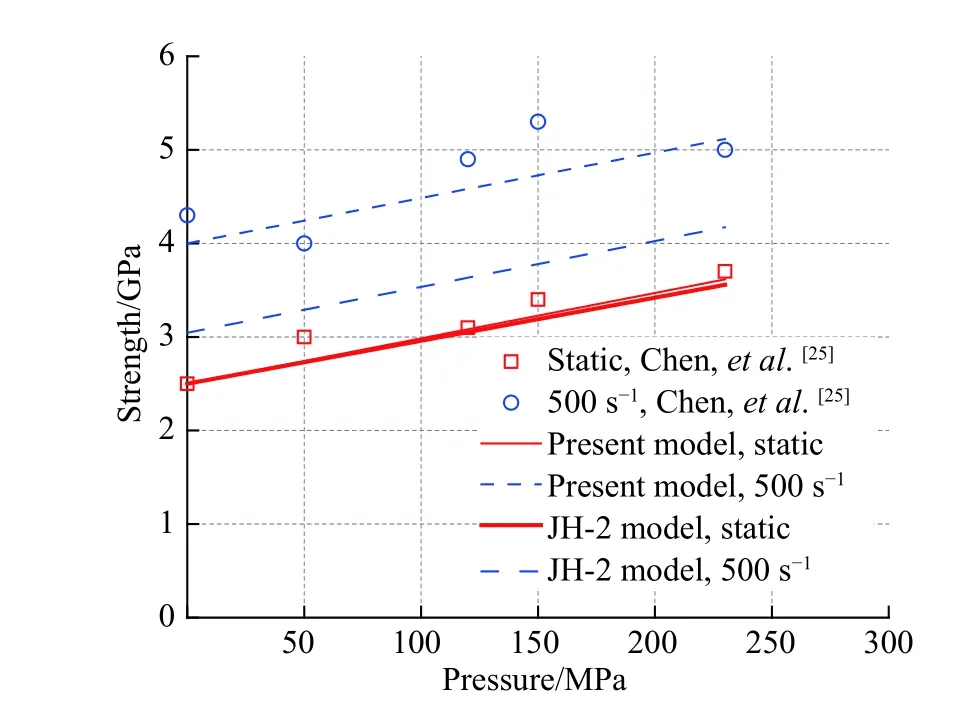
Fig. 5 Comparison between the experimental data[25] and the predictions by the present model of strength varies with pressure at different strain rates of AlN
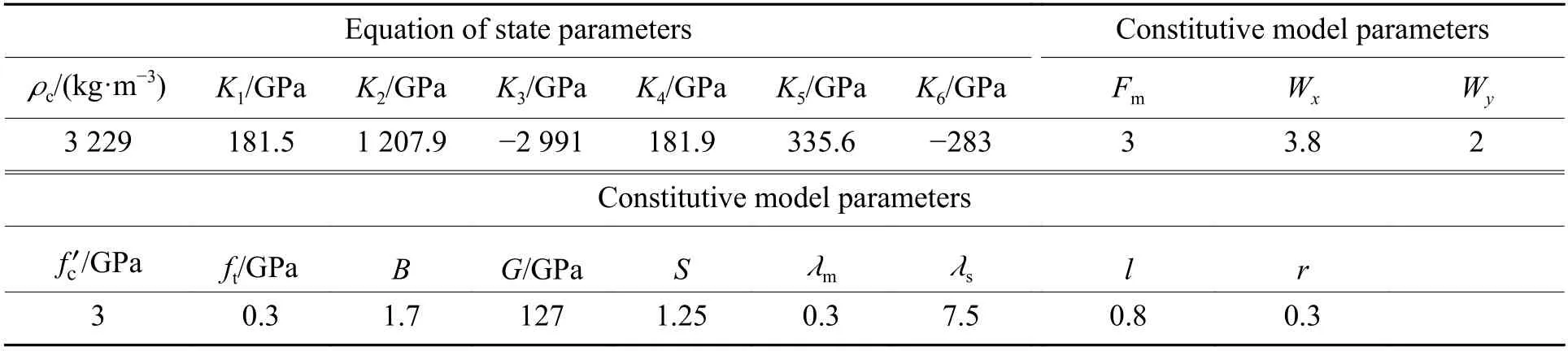
Table 2 Values of parameters for AlN in the present model

Table 3 Values of various parameters for AlN ceramic (JH-2 model)
Fig.6 shows the comparison of the numerically predicted stress-strain curves and the experimental data for BeO under triaxial compression with confinement pressures ranging from 0.1 GPa up to 1.0 GPa, as reported by Heard and Cline[26]. It is clear from Fig.6 that the numerical results are in reasonable agreement with the experimental observations.
Fig.7 shows variations of pressure and effective stress with maximum principal strain of AlN under quasistatic uniaxial tension. It is evident from Fig.7 that the numerical results from the present model give an elasticbrittle softening response of AlN under uniaxial tension with a principal tensile strength of 0.3 GPa for AlN. It is also evident from the figure that the mechanic behavior of the ceramic under uniaxial tension predicted numerically by the JH-2 model is elastic-perfectly plastic with the minimum pressure of 0.31 GPa and the maximum effective stress of 0.93 GPa, which are obviously not in compliance with the actual tensile behavior of the ceramic.
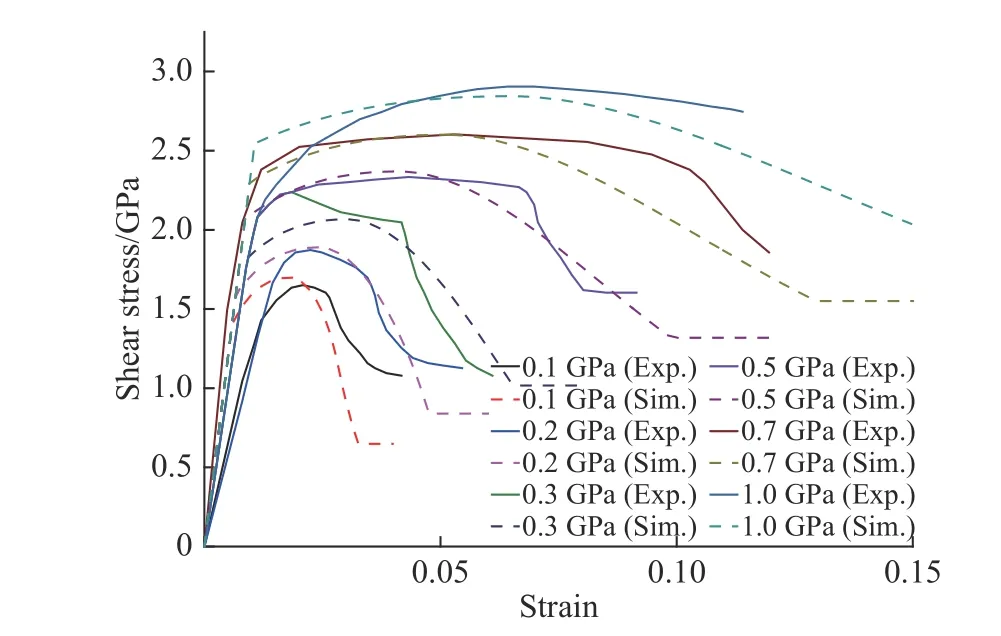
Fig. 6 Comparison of stress-strain curves for BeO under triaxial compression between the present model and experimental data[22]
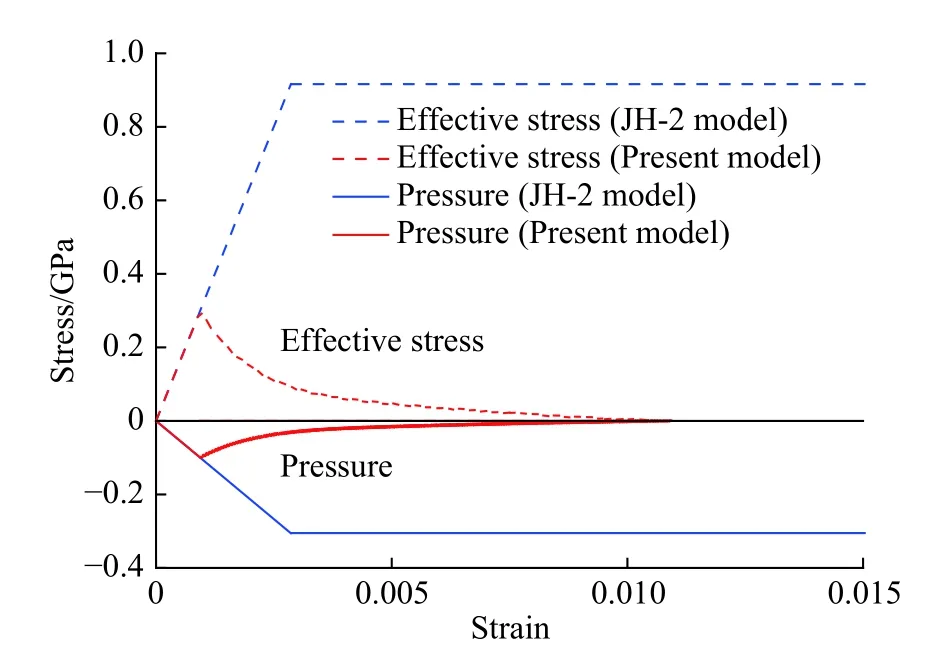
Fig. 7 Variation of pressure, effective stress with maximum principal strain for AlN under quasi-static uniaxial tension
Fig.8 shows variations of pressure and effective stress with maximum principal strain of AlN under quasistatic biaxial tension. Elastic-brittle softening response of the ceramic is predicted numerically using the present model under biaxial tension with a principal tensile strength of 0.3 GPa. On the other hand, an elastic-perfectly plastic response of the ceramic under biaxial tension predicted numerically by the JH-2 model have the minimum pressure of 0.31 GPa and the maximum effective stress of 0.48 GPa.
Fig.9 shows numerically predicted relationship between pressure and the maximum principal strain of AlN under both quasi-static triaxial tension. It can be seen from the figure that the present model predicts the elasticbrittle softening response of AlN under triaxial tension with quasi-static principal tensile strength of 0.3 GPa.Whilst the material is no longer able to withstand any loads after the maximum pressure reached according to the JH-2 model predictions. Furthermore, no strain rate effect is found under hydrostatic tension in the JH-2 model since it hasn’t taken into account the strain rate effect in tension.
Fig. 8 Variation of pressure and effective stress with maximum principal strain for AlN under quasi-static biaxial tension
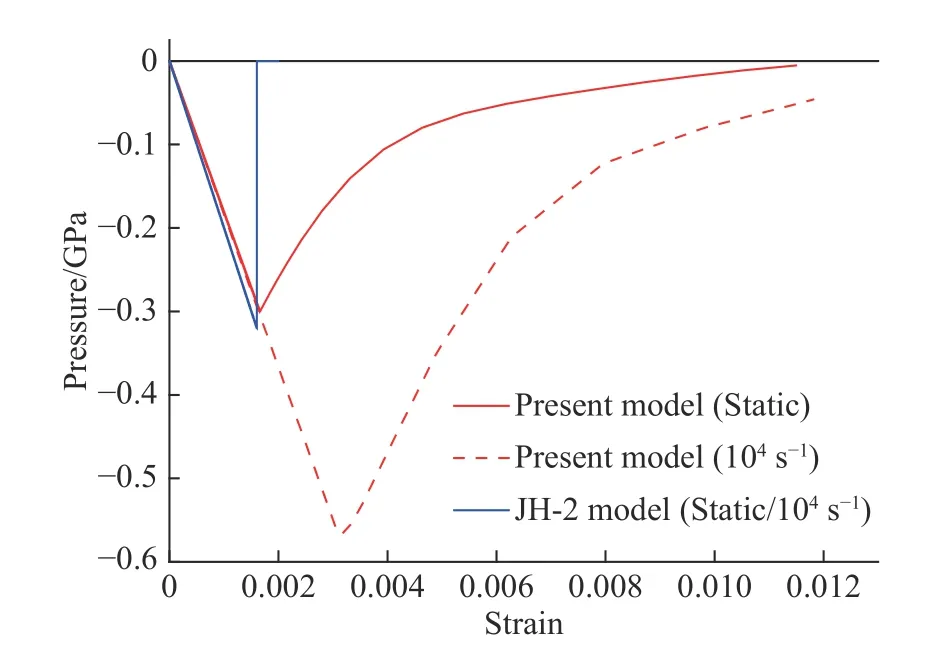
Fig. 9 Numerically predicted relationship between pressure and maximum principal strain of AlN under both quasi-static triaxial tension
3 Penetration of AD99.7/RHA Target
Numerical simulations are conducted in this section for the penetration of AD99.7/RHA target struck by flatnosed projectiles as reported by Lundberg[35]. In the experiments, long tungsten projectiles with length-todiameter ratio 15 were fired against the unconfined alumina with steel backing. The tests were carried out in three different scales with projectile lengths 30, 75 and 150 mm (corresponding diameters 2, 5 and 10 mm), respectively. The impact velocities were 1 500 m/s and 2 500 m/s. Fig.10 shows the schematic diagrams of the geometric dimensions of the projectiletarget combination. Table 4, Table 5 and Table 6 list the values of various parameters for AD99.7 ceramic material in the present model, tungsten alloy and RHA materials in the JC model. Parameters A1in the JC model is the initial yield strength under reference strain rate and reference temperature; B1, N1are respectively the strain hardening modulus and index; C1is strain rate hardening parameter; M1is temperature softening index;is the reference strain rate; cpis heat capacity; Tmand Trare the ambient temperature and the reference temperature(melting point), respectively; D1, D2, D3, D4and D5are failure criteria parameters; Csis the intercept of shock wave velocity-particle velocity (us-up) curve; S1, S2, S3are us-upcurve slope coefficient; γ0is Grüneisen parameter,A0is the first order volume correction of γ0.
Fig. 10 Schematic diagrams of the geometric dimensions of the projectile-target combination under the impact velocity of 1 500 m/s (Same materials used for all target configurations,and all configuration are axisymmetric.)
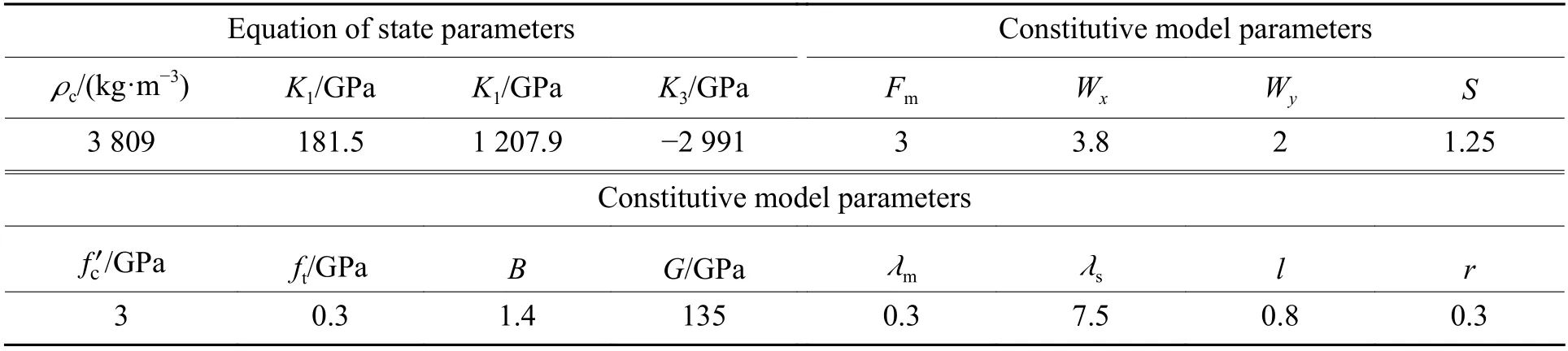
Table 4 Values of various parameters for AD99.7 ceramic[35] (The present model)

Table 5 Values of various parameters for tungsten alloy[35] (JC model)
Fig.11 shows the comparison of total penetration depth between the numerical predictions and the experimental data[35]. PTrepresents the sum of thickness of the ceramic and penetration depth in the RHA back plate, and Lpis the length of the projectile. In the figure, the solid symbols indicate the experimental data and the hollow symbols represent the numerical results by the present model proposed in this paper. The data of differentscales under the impact velocity of 1 500 m/s and 2 500 m/s are designated by square and triangle,respectively. For comparison, the numerical results obtained by Lundberg[35]with JH-2 model are also shown in Fig.11. The solid and broken lines represent the numerical results by JH-2 model at 1 500 m/s and 2 500 m/s respectively. It can be seen from Fig.11 that the numerical results from the present model are in good agreement with the experimental data. As can be seen from the figure that the numerical results for impact velocity of 1 500 m/s are in good agreement with the test data, whilst the results for impact velocity of 2 500 m/s are below the experimental observations[35].Thus, the JH-2 model has failed to produce consistent results as compared to the experiments.

Table 6 Values of various parameters for RHA[35] (JC model)
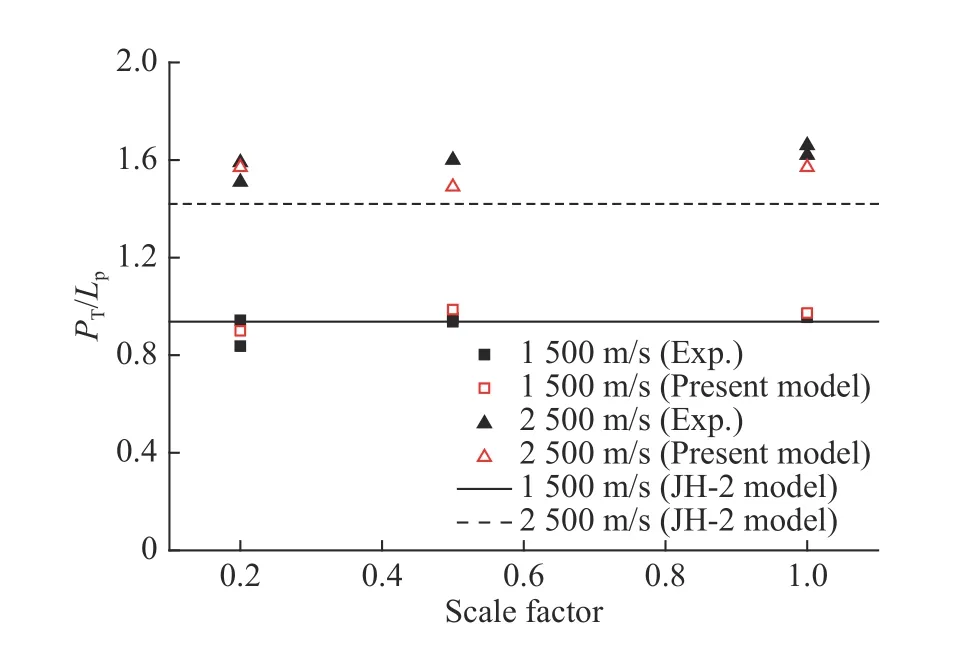
Fig. 11 Comparison between the numerical results and the test data for the depth of penetration in AD99.7/RHA targets by flat-nosed tungsten alloy penetrators[35]
4 Conclusions
A dynamic macroscopic constitutive model for ceramic materials has been developed by closely following the previous work on concrete. The model captures the basic features of the mechanical response of ceramic materials including pressure hardening behavior, strain rate effects, strain softening behavior, path dependent behavior (Lode angle), and failure in both low and high confining pressures. In particular, a new function is used to characterize the pressure dependent shear strength surface of ceramic materials which levels out at very high pressures, and strain rate effect is taken into consideration by dynamic increase factor which excludes inertial effect.
The present model has been compared with some available experimental data for ceramic materials. It transpires that the present model predictions are in good agreement with the experimental observations in terms of pressure-volumetric response, triaxial compression, quasi-static strength surface, dynamic strength surface, strain rate effect and depth of penetration. It also transpires that the present model is much more improved than the JH-2 model.
