Meromorphic Solutions of a Type of Complex Differential-Difference Equations
2020-07-28RENGuozhen任国珍GAOLingyun高凌云
REN Guozhen(任国珍),GAO Lingyun(高凌云)
(Department of Mathematics,Jinan University,Guangzhou 510632,China)
Abstract: Using Nevanlinna theory of the value distribution of meromorphic functions,we investigate the properties and expression of meromorphic solutions of a type of complex differential-difference equation,and we obtain some results,which are the extensions of complex difference equations to differential-difference equations.Example shows that our results are meaningful.
Key words: Complex differential-difference equation;Meromorphic solution;Value distribution
1.Introduction
Letf(z) be a meromorphic function in the whole complex plan C.We assume that the reader is familiar with the standard notation and results of the Nevanlinna theory of meromorphic functions[1−2],such as the characteristic functionT(r,f),proximity functionm(r,f),counting functionN(r,f).
The notationS(r,f)denotes any quantity that satisfies the condition:S(r,f)=o(T(r,f))asr →∞possibly outside an exceptional setEofrof finite linear measure∞.A meromorphic functiona(z) is called a small function off(z) if and only ifT(r,a(z))=S(r,f).Moreover,we use the notation degf Pfor the degree ofP(z,f) with respect tofand the order offis defined by
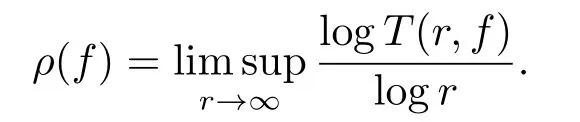
Many papers investigate solutions of some types of complex differential equations,and obtain some results[3−8].Recently,there has been renewed interests in meromorphic solutions of complex difference equations,in addition to the complex differential equation.Many authors have investigated complex difference equations,and obtained some results[9−15].
In 2005,Laine and Rieppo[14]considered a type of complex differential equations of the following form

wherePandQare relatively prime polynomials infover the field of rational functions,the coefficientsαJare rational functions andq=degf Q >0.They obtained the following results.
Theorem A[14]Assumef(z) is a transcendental meromorphic solution of the above difference equation,andf(z) has finitely many poles,it must be of the form
f(z)=r(z)eg(z)+s(z),
wherer(z) ands(z) are rational functions andg(z) is a transcendental entire function satisfying a difference equation of the form either

2.Some Lemmas
In order to prove our results,we need the following lemmas.
Lemma 2.1[14]Letfbe a non-constant meromorphic function and letP(z,f),Q(z,f)be two polynomials infwith meromorphic coefficients small relative tof.IfPandQhave no common factors of positive degree infover the field of small functions relative tof,then
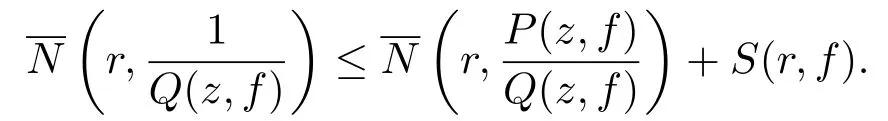
Remark 2.1[14]Iff(z) is a transcendental meromorphic function andP(z,f),Q(z,f)have rational coefficients,thenP(z,f(z))andQ(z,f(z))has only finitely many common zeros.
Lemma 2.2[16]Letf(z) be a meromorphic function and letΦbe given by

3.Main Results and Proofs
In this paper,letting
P(z,f)=ap(z)fp+ap−1(z)fp−1+···+a0(z),






where


猜你喜欢
杂志排行
应用数学的其它文章
- 具有惯性项和阻尼项的Cahn-Hilliard方程的整体吸引子
- 一角点支撑对面两边固支正交各向异性矩形薄板弯曲问题的辛叠加解
- Positive Solutions for Fractional Differential Equations with Integral and Infinite-Point Boundary Conditions
- Comparison Principle of Very Weak Solutions for Nonhomogeneous Elliptic Equations
- Global Existence,Asymptotic Behavior and Uniform Attractor for a Non-Autonomous Thermoelastic Timoshenko System of Type I with a Memory Term
- A m,p-Laplacian Parabolic Equation with Nonlinear Absorption and Boundary Flux
