基于响应面法的跌坎消力池优化设计研究

2020-07-28刁明军孙浩淼黄桂兵

西南民族大学学报（自然科学版） 2020年2期

任昱，刁明军，蒋雷，孙浩淼，黄桂兵

(四川大学水力学山区河流开发保护国家重点实验室，四川成都 610065)

底流消能是常见的泄洪消能方式[1，2].它具有良好的消能效果、适应性强，同时对周围环境影响较小，因而被广泛应用于水利工程中[3].消力池的设计对于消能率、安全性和工程造价至关重要. 消力池经常因为不合理的设计问题，导致底板失稳、空化空蚀等不良后果[4，5].消力池从结构形式上分为常规消力池、渐扩消力池、跌坎消力池等类型，常规消力池经常面临临底流速大、底板荷载集中的问题，往往应用于中小型水利工程.许多学者的研究表明，跌坎消力池可以将高流速的主体水流引离池底以射流的形式进入消力池，可以有效的降低消力池临底流速[6，7]，在工程上具有更为广阔的适应性.在跌坎消力池的结构参数中，跌坎高度，消力池长对消力池的消能率和工程造价影响很大.跌坎高度不足、消力池池长过短都会导致消能效果不佳，相反又会导致工程量增加，因此优化消力池的跌坎高度和消力池长度可以在节省工程造价的基础上，最大程度的提高消力池的消能率.

Flow-3D 软件近年来被广泛应用于数值模拟计算，王月华等[8]模拟闸下三级消能池方案验证了该软件模型具有可行性与实用性；张为等[9]采用FLOW -3D 软件模拟了块体与平底水垫塘内水流的运动特性；王青等[10]对陡坡弯道段的急流进行了三维数值模拟，并通过物理模型验证.

传统的试验设计方法往往计算量大，优化时间长，而且无法描述变量间的交互作用. 响应面法是结合数学和统计方法的优化设计方法，通过建立变量和响应目标之间的响应面函数，最终达到优化响应目标的目的[11].响应面法在生物和化工领域已经得到广泛的应用[12-14]，也有学者使用响应面法优化水轮机的设计参数[15]，因此可以采用响应面法对消力池的设计参数进行优化，采用统计学方法以较少的试验得到优化目标，以图形的方式直观的展示变量间的交互作用.本研究以消能率和工程经济函数为优化目标，跌坎深度D和消力池长L为变量进行13 组数值模拟试验，建立变量与优化目标之间的响应函数，求解最优组合，对消力池的结构参数进行优化.

1 优化目标函数

消力池的理想设计效果是消能效果良好且投资较少.因此，本研究采用消力池的消能率，工程经济函数两项作为优化目标.

1.1 消能率k

消力池消能率公式为：

式中：E1为隧洞末端断面比能消力池跃后断面比能，分别为隧洞末端和消力池后相对水深；v1、v2分别为隧洞末端和消力池后平均流速；α1、α2为动能修正系数，α1=α2= 1.

1.2 工程经济函数m

本研究将工程量定义为消力池开挖方量.取消力池体积的倒数值为工程经济函数，即消力池跌坎体积越小，投资越少，工程经济函越高，越符合实际需求.如图1 所示为消力池体型参数.其中设计变量为跌坎深度D和消力池长L，其他变量为常数.

消力池经济函数公式：

式中：h为隧洞高度，h=12m ；H为消力池高度，H=(10 +h+D)m；d为消力池尾坎高度，d=6m；b为隧洞宽度，b=6m；l1为消力池尾坎斜坡段水平投影，l1=3m；l2为消力池尾坎长度，l2=3m；B为消力池宽度，D=18m.

1.3 综合优化目标函数Y

本研究为多目标优化问题，多目标优化是向量函数的优化，对于多目标优化问题，常用的方法有两种.一是直接法，直接求出非劣解，然后在选择较好的解；另一种是间接法，构造权函数将多目标优化问题转化为单目标优化问题.本研究根据优化目标的消能率k和工程经济函数m重要程度采用不同的权重，将多目标优化问题转化为单目标优化问题.

图1 消力池体型参数图Fig.1 Shape parameters of stilling basin

一般情况下提高消能率就需要加深跌坎深度、增加消力池长度，因此必然使得工程经济函数增加，在工程中可以结合实际情况有所侧重. 本研究综合考虑，选取两者权重比为3：2，使用Design Expert 软件中的importance 功能定义最终综合目标函数.其表达式为：

式中，Y为综合目标函数；ρ1、ρ2为各项的权重系数，分别为3、2.

1.4 归一化处理

为了避免设计变量间的量纲影响或变量取值范围的变化较大，对设计变量进行归一化处理，其计算公式为：

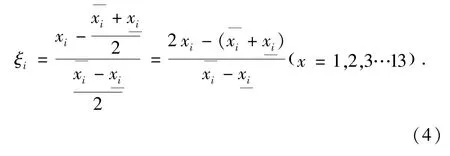
2 试验设计

本研究中的水库泄洪洞由导流洞改建，原导流洞宽6.0 m，采用龙抬头的方式进行改建，改建段隧洞宽度由6.0 m 渐变为8.0 m，其后隧洞宽8.0 m，隧洞全长372. 0 m，库区水位至隧洞出口底板落差60.0 m，下泄水流采用底流消能.

采用响应面法利用Design Expert 软件进行试验设计.相比于正交试验其优点是可以用统计学的方法以较少的试验得到想要的结果.根据设计规范和相关学者的研究，跌坎深度D取2 m ～8 m，消力池池长L取70 m ～100 m.表1 为各变量的水平取值，其中x1、x2分别为D、L的归一化结果.

表1 响应面优化设计2 因素水平Table 1 Response surface optimization design 2 factor levels

试验共计13 组(见表2 所示)，其中后5 组为中心点重复对照试验.

表2 试验设计及数值模拟结果Table 2 Test design and numerical simulation results

3 数学模型

数值计算域为从上游库区至消力池出口后下游100m 的范围.计算域网格采用结构化网格划分，并对泄水建筑物进行局部加密，总网格数约300w，计算域和网格划分如图2 所示. 进口边界采用压力进口，上游水位为799.00m，出口边界采用自由出流，左右采用固体边界，顶部采用压力进口，压力为正常大气压，底部采用固体边界，这种计算方法已经被许多学者证实有较高的可靠性和计算精度[8-10].

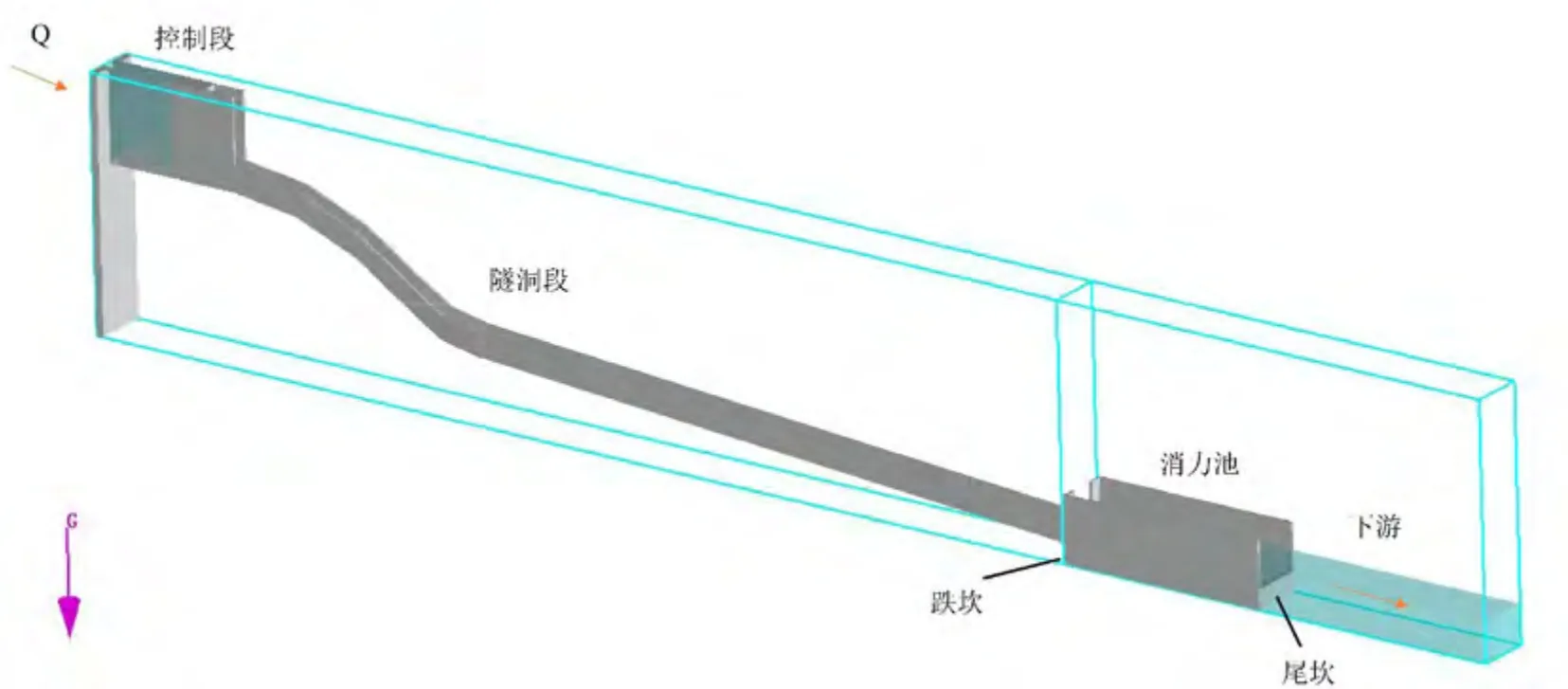
图2 计算域网格划分Fig.2 Grid generation of computing domain

4 显著性分析与交互作用

消能率的试验数据进行方差分析和显著性检验结果见表3. 结果表明：消力池的跌坎深度D和消力池长L对消能率影响较大，前者的显著性概率P ＜0.01 ，后者的显著性概率P ＜0.05 .目标函数Y的响应面模型P值小于0.05，表明该响应面模型对Y影响显著.对数据进行回归拟合，建立以消能率为响应值的RSM 代理模型为：

表3 消能率方差分析表Table 3 Analysis of variance of energy dissipation rate

试验设计区间内，该代理模型回归显著(P＜0.05)，其决定系数Radj2=0.8072. 说明该模型能解释80.72% 以上的响应值变化.

对工程经济函数的试验数据进行方差分析和显著性检验结果见表4.结果表明：消力池的跌坎深度D和消力池长L对工程经济函数影响较大，两者的显著性概率P ＜0.01 ；目标函数Y的响应面模型P值小于0.01，表明该响应面模型对Y影响极为显著.对数据进行回归拟合，建立以工程经济函数为响应值的RSM 代理模型为：

表4 工程经济函数方差分析表Table 4 Analysis of variance of engineering economic function

试验设计区间内，该代理模型回归显著(P＜0.01)，其决定系数Radj2=0.9998. 说明该模型能解释99.98% 以上的响应值变化.

分析可知，跌坎深度和消力池长分别对消能率和工程经济函数影响显著，其的交互作用对工程经济函数影响极为显著，两变量间的交互作用显著性概率P＜0.01 ，这是因为同时增加跌坎深度和消力池长会使得消力池体积显著增加.图3 为跌坎深度和消力池长度对综合目标函数Y的交互作用.

由图3 可知，当D取较小值(2m ～ 5m)时，综合目标函数随着L的增加先迅速增加后降低，当D取较大值(5m ～8m)时，综合目标函数随着L的增加而降低.这说明，当跌坎高度小于5m 时，综合目标函数值波动不大，趋于中间水平；当跌坎高度大于5m 时，在消力池长取值范围内长度越小综合目标函数值越大.当L取较小值(70m ～85m)时，综合目标函数随着D的增加迅速增后趋于稳定；当L取较大值(85m ～100m)时，综合目标函数随着D的增加而降低，且整体函数值偏低.说明综合考虑消能率和工程经济函数的情况下，在变量取值范围内跌坎深度的增加相比于消力池长的增加可以显著提高消能率，跌坎深度的增加会使得工程量增大. 因此综合考虑，优化区间内当即D=7.07m、L=70.0m 时综合目标函数Y取最大值0.734.

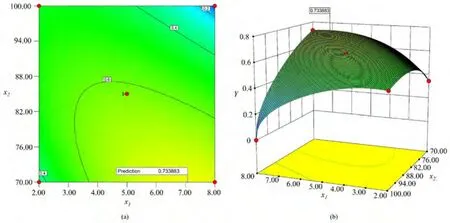
图3 跌坎和消力池长对综合目标函数的响应Fig. 3 Response of drop sill and stilling basin length to comprehensive objective function

5 优化结果分析

图4 为优化后消力池的整体流态，从图中可以看出消力池流态良好，无明显旋涡、翻滚，尾坎出流水流无明显二次跌落.消力池消能率62.68%，最大出池流速5.27m/s.相比变量区间内的消能率最差的体型，以工程经济函数提高17.60%的情况下，消能率提高了20.88%；相比变量区间内的工程量最大的体型，节省30.78%的工程量，消能率仅降低了6.91%. 可以看出经过优化，消力池可以在节省工程投资的前提下最大程度的提高消能率.