一种交叉验证和距离加权方法改进的KNN 算法研究
2020-07-28黄光华冯九林
黄光华, 殷 锋, 冯九林
(西南民族大学计算机科学与技术学院, 四川 成都 610041)
大数据时代,互联网数据的爆发式增长导致数据出现了密度高,维度复杂等一系列数据问题,如何有效的对这些数据进行归类存储已经成为信息检索、数据库管理、数据挖掘和数据分析等领域亟待解决的关键问题之一.在众多的分类算法中,KNN算法以适用于样本容量较大的类域自动分类著称,对于新时代背景下涌现出的海量数据处理难的问题,KNN算法的上佳表现确实为业界称道.
1 KNN 算法及其缺陷分析
K-最临近(K -NearestNeighbor)算法[4]是著名的数据挖掘分类算法.核心思想是在向量空间模型中进行决策归类分析,将一个待分类对象视作一个n维向量,将其放入一个特征空间中,这个特征空间由m个已经训练好的特征向量构成,这m个特征向量属于多个不同的类别集ε∈ (1,2,3…,η),设该待分类对象和向量空间中的m个特征向量的距离为D=(D1,D2,D3,…Dm) ,给定一个基准k,从D中按照从小到大的顺序选出k个值,查看这k个值分别属于哪一类数据,该待分类对象最后将被分类至类别出现次数最多的类中.
在KNN 算法中,欧式距离是被较频繁使用到的距离度量方法.使用这个距离,欧氏空间成为度量空间.对于两个n维向量x和y,两者的欧式距离定义为:

其中, (xi,yi) 为数据点i的坐标值,D 值为数据点i与j之间的距离.
KNN算法的步骤如下:
①输入一个待分类数据对象x,计算它与训练集T中的每个样本数据对象的距离,并设置基准值k.
②寻找出待分类对象x与训练集T中的样本数据对象距离最近的k个样本数据对象.
③对②中寻找到的k个样本数据对象在类型集合ε中进行类型匹配,找出包含最多个数的类.
④将待分数据x划分到(3)中包含次数最多的类中,结束此次匹配.
KNN算法在大样本的情况下对试验样本有较强的一致性结果. 但是KNN需要一个较大的样本空间来对数据进行测试,算法每一次对测试数据的分类都是在样本全局的基础上进行的,这就对较大的物理内存空间产生了必然性要求(用以存放数据);且KNN算法在训练数据集不平衡时,即数据集中的某一个类所拥有的数据占整个数据集中的数据量比例较大时,在搜索k个邻居时,得到的结果将偏重于拥有数据较多的类,这种情况下所得的预测结果偏差相对较高.
2 交叉验证和距离加权方法改进KNN算法-WCKNN(Weighted cross -validation KNN)
2.1 改进分析
在数据集有限的情况下使用k折交叉验证[5-6],将原始数据集均分成C组,每一次将其中的C-1 组数据作为训练集,以用于建立模型,剩下的1 组数据做为验证集,这样会同时通过训练得到C个模型,通过平均k次验证的结果,最终得到一个单一评测结果作为该模型真实分类率,k折交叉验证充分利用了数据集对算法效果进行测试. 如果这C个模型的均值(即真实分类率)效果良好的话,那么在一定程度上这个模型就有了一定的泛化能力.
我们首先应该明确一点,当给定了k值以后,在使用传统的KNN算法得到的排序数组必定有一个或多个分类,这些分类即是和待分类对象最接近的已分类对象.无论返回的结果是否正确,在一般情况下,使用传统KNN算法得到的排序数组中会存在正确的结果.
其次,对于KNN算法或者改进的KNN算法而言,训练集和测试集的数据是透明的,无论我们对算法做出何种改变,测试集都只是用来验证算法最终的普适度.即:用测试集去测试我们改进的正确性,当测试集对于改进算法表现出比较好的普适度时,就可以利用这种改进去测试一个新的样本,对未知的样本进行分类.
我们已经知道,在传统的KNN算法测试中,何种类别出现的多,那么就把当前的测试样本划分为哪一类.所以显然的,我们可以将本次实验中某类出现的次数li和当前选取的k值之比作为分类结果为某类的概率pi,即:

那么在传统的KNN算法实验中,对于某个测试样本,若某两种类别出现次数差距较小,即概率之差:
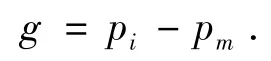
非常小,那么使用传统KNN算法得到的结果对于该待测样本来说就可能具备了模糊性. 相反的,若使用传统KNN算法得到的可能出现类别的个数是唯一的,那么对于该待测样本而言,传统的KNN算法能够良好的预测此次结果.
所以,若我们在某次测试中,用传统的KNN算法得到的分类概率是多分布的,即在KNN算法求得的排序数组中出现了多个可能分类,且出现概率最大的两个类别的概率之差g非常小,理论上,我们就将其他出现概率小的类别近似视为不可能类别,将该两类出现概率最大的类别视为极大可能类别.
于是,在上述k折交叉验证理论和分类概率pi的基础上提出WCKNN算法,算法的主要思想为在某两类分类出现概率之差非常接近时增加距离加权验证,根据类别加权距离之和的平均作为评断分类结果的标准若传统的KNN算法得到的类别数是唯一的,则不进行加权.
首先我们需要确定距离加权验证的次数,传统的KNN算法是根据待测点和k个最邻近点的距离比较来确定待测点的分类,因此对改进的KNN算法而言,我们不希望因为k值的变动而造成加权验证次数的变动.我们发现对于函数:

当x的取值大于0 时,其值恒为1,所以无论k值根据经验取多少时,都不会影响加权次数,由此我们确定距离加权验证的次数为1 次.
在确定了距离加权的次数之后,我们便可以开始考虑如何分配我们的权值了. 传统的KNN算法以距离为核心,根据k值选取训练集中前k个离测试点最近的点.我们以加权的思想再深究之,便可以对KNN算法从另外一个角度有一个新的理解.即:
距离越小,权值越大.距离越大,权值越小.
那么参考函数:

f(x) 在整个实数集中的函数值恒大于0,其对称轴为x=u,我们将u取为1.a决定了函数的定点高度,我们将之取为k,σ为方差,我们将之取为1,这样f(x) 就是一个正态分布了.对于指定的k我们就可以产生一一与之对应的权值了.
因为我们将某两种出现次数最多的类别视为极大可能类别,所以在进行加权计算时,为了简化运算量,只需要将权值与极大可能类别中的元素一一相乘,这样就得到了我们需要的加权距离. 但是这时候若我们直接对新的加权距离进行重新排序,那么结果仍然不会有任何改变,这是因为我们并没有改变某种类别出现的次数,同时根据距离越小,权值越大的理念,即使让传统的KNN算法得到的排序数组组内序列发生变化,若仍然以类别出现次数之和来作为分类评判标准,则是徒费力气.
那么,同样根据传统KNN算法的思想,既然传统的KNN算法是以类别出现的次数之和来进行分类,我们简单的称这种思想为归一化思想.那么在本次加权改进中,我们可以延续这种归一化的思想,将加权后属于相同类别下的加权距离进行归一化,再对极大可能类的每一类的距离总和分别求平均,那么依据距离越小,权值越大的思想,实验的结果就应该就是加权距离之和平均更大的那一类.
2.2 WCKNN 算法流程:
步骤1:将原始训练集划均分为c- 1 个子训练集,余下的一个子集作为验证集,从验证集中取出数据对象xi,xi∈x= {x1,x2,x3…xn}
步骤2:根据传统的KNN算法,得到本次分类的原始距离排序数组.
步骤3:根据经验值k 和函数:

确定加权次数,使得加权次数不会受k值的影响.
步骤4:计算类别出现概率,若有多个类别出现,选取出现概率之差最小的两个类别,根据高斯函数:

取定权值,一一相乘后得到新的加权距离.
步骤5:对同属一类的加权距离进行求和,加权距离总和与出现次数之比,即加权平均距离更大的类别即为本次改进实验的实验结果.
步骤6:实验采用的是5 -折交叉法,所以重复步骤1 到步骤6 共计5 次,注意在步骤1 中确保每次的验证集不相同,最后统计5 个模型下的分类正确率,得到分类正确率的均值作为WCKNN算法的最终分类正确率,以验证WCKNN的正确性.
步骤7:不断改变k 值,重复步骤1 -6,得到不同k 值下的WCKNN的正确率,为最后的实验对比打下数据基础.
2.3 WCKNN 算法的伪代码描述
现根据改进分析及算法流程给出改进WCKNN算法的相关伪代码. 其中k是近邻数量,testdata是测试集,traindata是训练集,cls是实验数据的所属类别.

3 实验结果与分析
3.1 实验数据
为了验证算法的准确性,我们采用WCKNN算法进行手写体数字的识别[2].在实验中不断改变每个测试数据的邻居数量k,验证不同k值下改进算法的正确率.
手写体数字的原始总体样本为10 000 个手写体数字,经过5 -折交叉法建立5 个模型后,得到实验数据,并去除异常数据(如距离为0,表示本次测试样本和训练集里的样本重合,不应当纳入实验结果考虑范围)后,使用WCKNN算法不断对k值进行改变,由于篇幅有限,只给出表1 和表2 的实验数据,表中描述的是两种算法的正确率,num是K折交叉验证中每折的数据量,也即每次测试集的数据量.

表1 实验数据(跨度为1)Table 1 Experimental data (span is 1)

表2 实验数据(跨度为5)Table 2 Experimental data (span is 5)
由表1 和2 可知,对于本次实验采用的对手写体数字进行识别的实验而言,WCKNN算法的最佳k值为6,对于不同的k值,WCKNN算法都基本上保证了识别的正确率比传统的KNN算法高.
3.2 实验结果分析
为了方便比较 WCKNN 算法和 KNN 算法的关系,将实验数据绘制成图1.

图1 算法分类正确率对比图Fig.1 Algorithm correct rate comparison chart
从图1 可以看到,使用WCKNN算法在不同的k值下的得到的分类准确率,较直接使用传统KNN算法得到的分类准确性要高,所以使用WCKNN算法一定程度上可以增加我们分类的准确性,且在手写数字识别实验中,分类效果峰值差距达到了1%左右,此也验证了2.1 改进分析的正确性,进而验证了改进算法的正确性.从实验结果(表2)可知,当k值较大时,传统的KNN算法收敛的速率较大,而改进的WCKNN算法的收敛速度则更加缓慢一些,由此可知,改进的KNN算法分类结果更加稳定,更加适合用于数据分类.
4 结束语
KNN 算法每一次都是在样本全局的基础上去进行归类计算,这在很大程度上消耗了空间,增大了算法空间复杂度,本文通过交叉验证的形式,通过建立不同的模型,相比于传统的KNN 算法,降低了空间复杂度.且传统KNN 算法在样本分类不平衡时,预测偏差相对偏高,本文通过对距离机制方面的研究和改进,通过激活函数进行加权,通过实验结果分析可知,在样本分类不平衡时,WCKNN 算法的预测偏差要低于传统的KNN 算法,分类更具有代表性,达到了预想的效果.但是改进的WCKNN算法仍具有进一步的提高空间,首先是没有解决出现概率之差的阈值的自动选取,目前的策略是人为的进行选取阈值,这是一大缺陷,其次WCKNN算法并没有根本上解决传统KNN算法的k值的选取较多的依赖于经验的问题,只是能根据不断的实验确定最佳k值而不能自适应k值,而k值的选取也会在一定程序上对分类的正确性有所影响,这些将会是在今后的试验中值得去研究和改进的方向.
