一类带强阻尼Kirchhoff 型吊桥方程的长时间动力学行为

吕鹏辉，腾 旭，吕小俊

(云南大学旅游文化学院信息学院， 云南丽江 674199)

1 引言

本文研究一类带强阻尼Kirchhoff 型吊桥方程的长时间动力学行为：

其中Ω 是RN中具有光滑边界的有界域，其光滑边界为Γ，其中k2是弹性系数，有关M(‖∇u‖2)，f(x) 的假设将会在后文中给出，函数

吊桥方程是在1990 年，A.C.Lazer 和P.J.Mckenna 在研究非线性分析领域的问题时，提出一新的模型，即吊桥方程.该模型提出来后，相当多学者对该类吊桥方程进行了相关研究，参见文献[1 -7，10 -11]及相关文献.Ivana Bochicchio，Claudio Giorg 和Elena Vuk[1]研究了可延展吊桥方程的长时间阻尼动力学.2011 年，JONG-YEOUL PARK 和JUM-RAN KANG[2]得到了非线性阻尼吊桥方程的整体吸引子的存在性.2018 年，黄商商和马巧珍[3]在使用了能量估计和收缩函数的方法的情况下，得到了在弱拓扑空间下存在全局吸引子.2018 年，贾澜和马巧珍[5]运用加强的平坦条件，在较弱的非线性项条件下，得到了基尔霍夫型吊桥方程的指数吸引子的存在性.受以上分析和相关参考文献的启示，在本文中，我们运用算子半群分解的方法研究一类kirchhoff 型吊桥方程的长时间动力学行为.

2 预备知识

当s= 0 时，记H=L2(Ω )；当s= 2 时，记V2=H2(Ω )∩H10 (Ω )，且其相应的内积和范数分别为

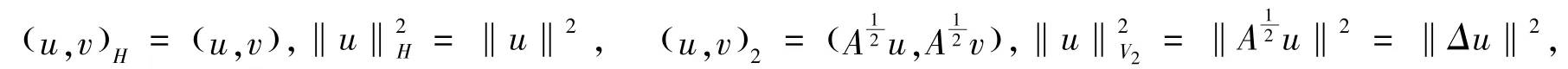
‖Au‖表示D(A)的范数，其中A=Δ2.显然V4⊂V2⊂H⊂V-2，其中V-2为V2的共轭空间.

接下来定义Hilbert 空间并赋予范数：

为了得到问题(1.1) -(1.3)的长时间动力学行为，我们接下来给出相关概念：

定义2.1[8](整体吸引子)设X为一Banach 空间，{S(t)}t≥0是一连续算子半群，若存在紧集A0⊂X满足下列条件：

(I)不变性：在算子半群{S(t)}t≥0的作用下是不变集，即S(t)A0=A0( ∀t≥0)；

(II)吸引性：A0吸引X中的所有的有界集，即任意B⊂X是X中的有界集，则

特别地，当t→ ∞ 时，从u0出发的一切轨道S(t)u0收敛于A0内，即有dist(S(t)u0，A0)→0(t→ ∞ )，

则称紧集A0为半群{S(t)}t≥0的整体吸引子.

定义2.2[8，10](指数吸引子)设{S(t)}t≥0是一完备度量空间X的算子半群，如果M⊂X满足下列三个条件，则称集合M⊂X为半群{S(t)}t≥0的指数吸引子：

(Ⅰ)集合M在X中是紧的，并且存在有限维的分形维数；

(Ⅱ)集合M是正不变的，即S(t)M⊂M；

(Ⅲ)集合M⊂X是半群{S(t)}t≥0的指数吸引集，即对每个有界集B⊂X，存在常数c=c(B)，τ ＞0 ，使得dist(S(t)B，M)≤c(B)e-τt.

定理2.1[9]在Banach 空间X中定义一连续算子半群{S(t)}t≥0，若满足下列条件，则连续算子半群{S(t)}t≥0存在整体吸引子：

(I)存在一有界吸收集B⊂X，使得对任何有界集B0⊂X， 满足dist(S(t)B0，B) →0 (t→+ ∞ ).

(II)S(t) 可分解为S(t)=P(t)+U(t) ， 其中P(t) 是X→X的连续映射且对每个有界集B0⊂X， 使得

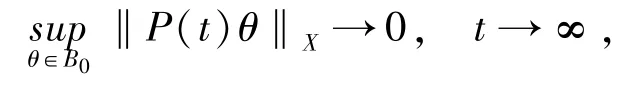
当t充分大时，U(t) 为一致紧，即对任意一有界集B0⊂X，都存在T0=T0(B0)，满足在X中为相对紧.

定理2.2[10]设X3⊂X1是一不变紧子集，而且X2紧嵌入X1，若存在时间t*，使得下列条件都成立：

(Ⅰ)映射(t，z0)S(t)z0，即 [0 ，t*]×X3→X3是 Lipschitz 连续的；

(Ⅱ)映射S(t*)：X3→X3有如下分解形式：

其中S0满足其中C*＞0 ，则半群{S(t)}t≥0存在指数吸引子.

3 整体吸引子的存在性

定理3.1假定

(H1)这里λ1为 -Δ的第一特征值.

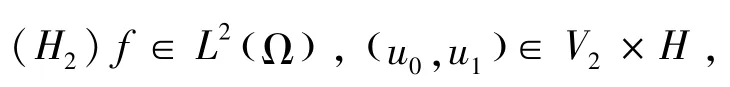
问题 (1.1)- (1.3) 存在唯一整体解u∈L∞(0，+ ∞；V2) ，ut∈L∞(0，+ ∞；H) .

注3.1 对于M(s)的假设，允许M(s)退化，即M0= 0 ，问题(1.1)-(1.3) 也存在唯一整体解u∈L∞(0，+ ∞；V2) ，ut∈L∞(0，+ ∞；H) .

证明：方程(1.1)分别与ut和作H内积得到

(3.1) +(3.2)得到

由假设条件(H1) 、(H2) 得到：

将(3.5)代入(3.3)得到

我们应用Gronwall 不等式，得到：

接下来，证明解的唯一性.

令u(t)和v(t)分别为初值为(u0，u1)，(v0，v1)的两个解，则w(t)=u(t)-v(t)满足

用wt和(3.10)作H内积，得到

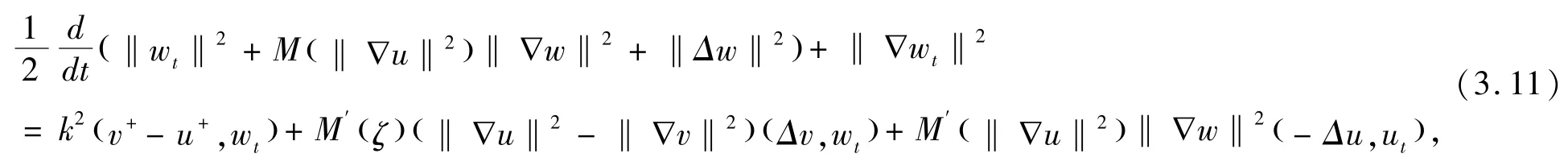
结合假设条件及相关重要不等式(Young 不等式，Holder 不等式和Poincare 不等式)，得到

将(3.12) -(3.13)代入(3.11)得到

运用Gronwall 不等式，则得到

证毕.

由定理 3.1，令B= {(u，ut)∈X1：‖ut‖2+ ‖Δu‖2+k2‖u+‖2≤R2} ，则B是半群{S(t)}t≥0在X1中的有界吸收集.从而有下列定理：

定理3.2在定理3.1 假设条件下，则球B=BX1(0 ，R2) 是问题(1.1)生成的解半群{S(t)}t≥0在X1中的有界吸收集，即对X1中任意有界集B1，存在t1=t1(B1)，使得当t≥t1(B1)时，有S(t)B1⊂B.

推论3.1在定理3.1 假设条件下，对任意R ＞0 和初值z0=(u0，u1)，存在t1=t1(R)，当 ‖z0‖ ≤R时，‖S(t)z0‖X1≤R2，∀t≥t1成立.

接下来，利用解分解方法证明相关引理.

设u=v+w， 其中

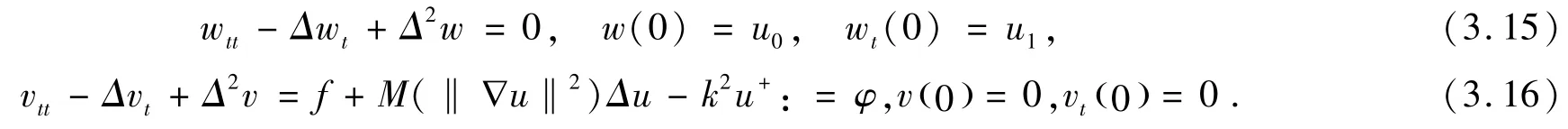
引理3.1如果 (u0，u1) ∈B， (w，wt) 是(3.15)的解，则

证明：(3.15)分别与与wt，εw作H- 内积得到

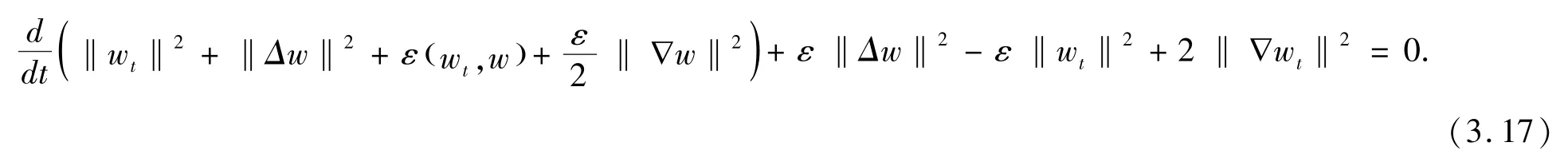
由假设条件，则存在正常数κ，ρ，使得

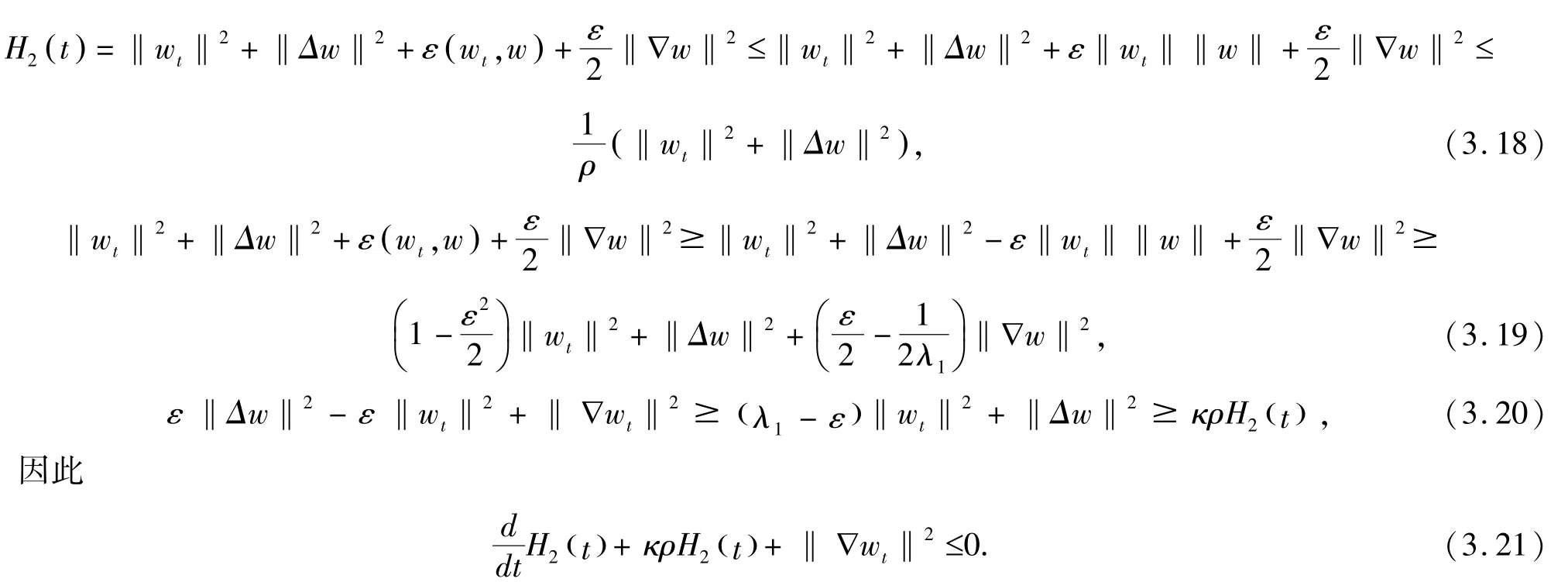
通过Gronwall 不等式得到

证毕.

引理 3.2如果 (u0，u1) ∈B， (v，vt) 为(3.16)的解， 则存在紧集N(T) ⊂X1且 (v，vt) ∈N(T).

(3.24)中的方程与η作H- 内积得到

由假设条件

结合(3.26) -(3.29)得到

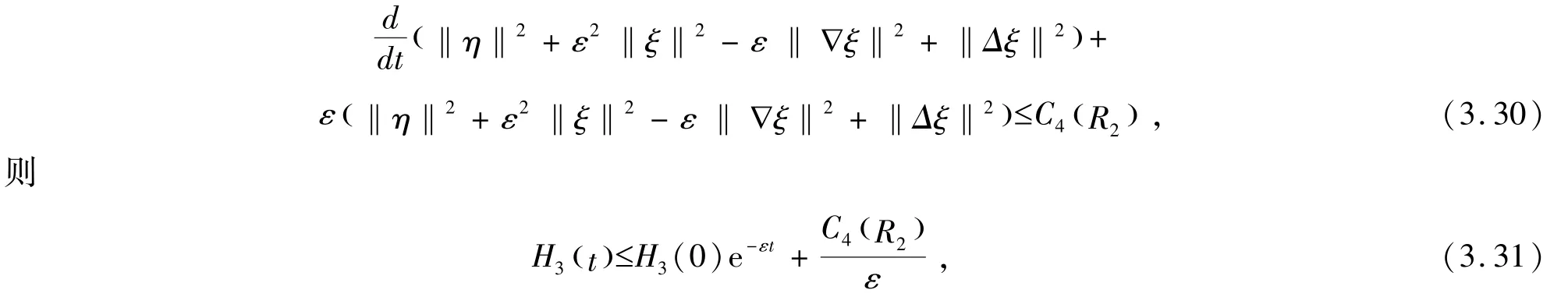
其中H3(t)= ‖η‖2+ε2‖ξ‖2-ε‖ ∇ξ‖2+ ‖Δξ‖ . 由H3(0)= 0 ， (3.31)变换为

随后得到

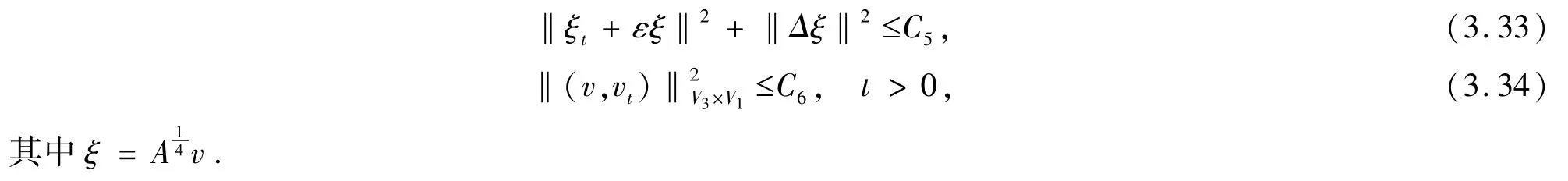
因为V3×V1→X1是紧嵌入， 即说明V3×V1的有界集为X1的紧集.

证毕.

定理3.3在定理3.1 的假设条件下，由问题(1.1) -(1.3)生成的连续解半群{S(t)}t≥0在X1中存在紧的整体吸引子.

证明：定义：P(t)(u0，u1)= (w(t)，wt(t))，U(t)(u0，u1)= (v(t)，vt(t)).

则S(t)=P(t)+U(t) . 由引理 3.1 可知：任意的 (u0，u1) ∈B⊂X1， 算子P(t)：X1→X1是连续的，并且满足定理2.1 中的(Ⅱ). 同时， 由引理3.2 可知：U(t) 是一致紧的. 再根据定理3.2，存在有界吸收集，所以{S(t)}t≥0在X1中具有紧的整体吸引子.

证毕.

4 指数吸引子的存在性

定理4.1在满足定理3.1 的假设条件下，则球B2=BX2( 0 ，R3)是由问题(1.1) -(1.3)生成的连续解半群{S(t)}t≥0在X2中的有界吸收集，即对X2中任意有界集B1，存在t1=t1(B1)，使得当t≥t1(B1)时，有S(t)B1⊂B2.

证明：由(1.1)分别与 -Δut和ε(-Δ)u作H内积得到：

结合假设条件和定理3.1 中的有界性及Holder 不等式、Young 不等式以及Poincare 不等式，得到

结合(4.3) -(4.4)，整理得到

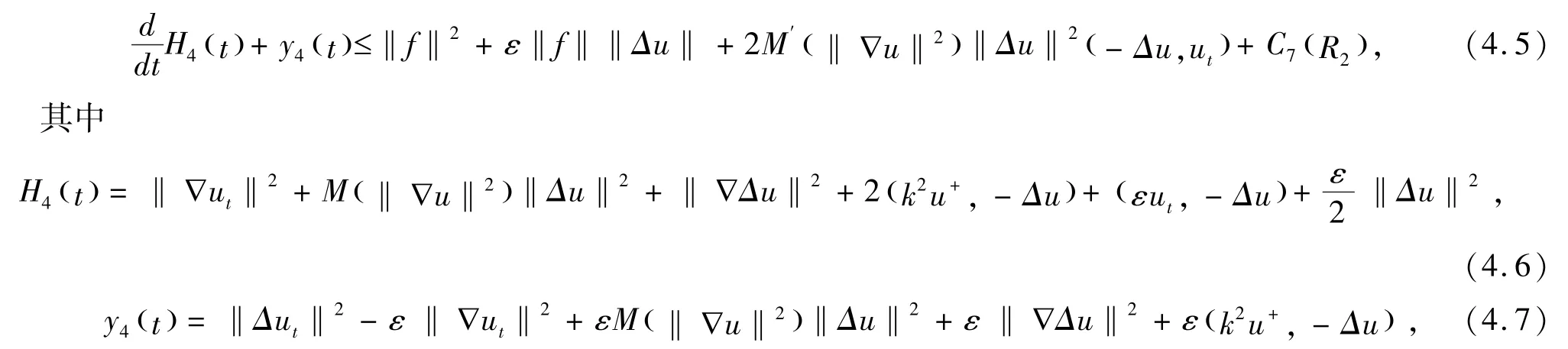
类似于定理3.1 处理方法，且结合定理3.1 的结论，存在κ得到

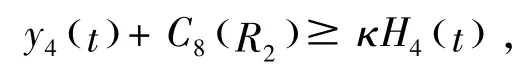
则(4.5)化为

利用Gronwall 不等式，得到

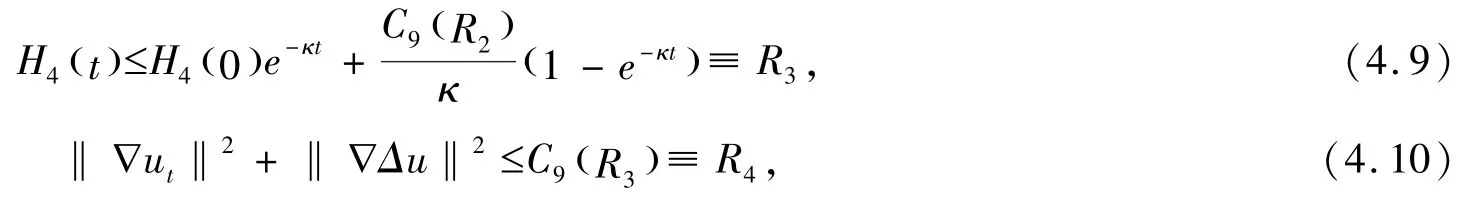
所以，若u是方程(1.1) -(1.3)的解，令其中

所以，B2是由问题(1.1) -(1.3)生成的连续解半群{S(t)}t≥0在X2中的有界吸收集.

定理4.2对任意的初值z1=(u10，u11)，z2=(u20，u21)∈X1和任意的R ＞0 ，使得 ‖zi‖X1≤R，那么存在常数P，有 ‖S(t)z1-S(t)z2‖X1≤ePt‖z1-z2‖X1，∀t∈ [0，∞) ，其中P是与λ1、ε、k和R2有关的常数.

证明：此定理的证明过程与前文证明解的唯一性的过程相似，此处不再祥写.

定理4.3在定理3.1 假设条件下，存在常数C ＞0 ，使得

其中z0=(u0，u1)，z(t)=(u(t)，ut(t))。

结合定理3.1、定理3.2 和相关假设，得到

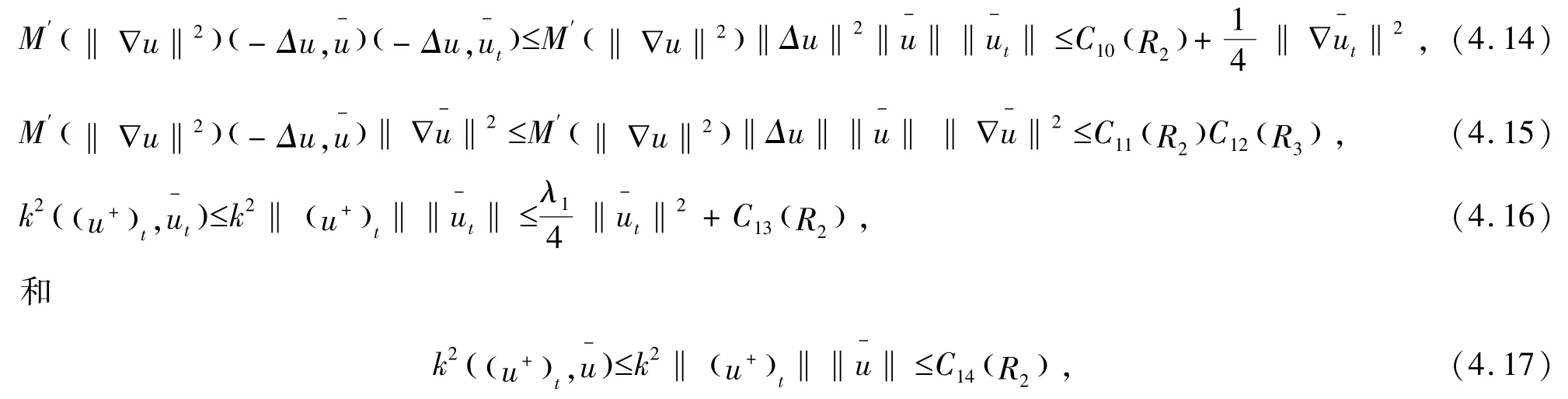
由(4.12) -(4.17)，得到

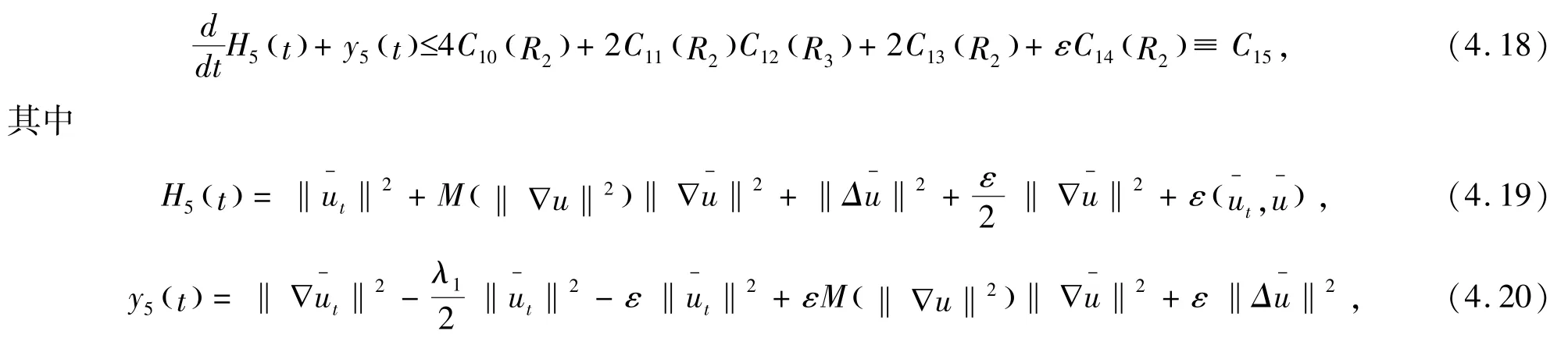
易得，存在κ，ρ：y5(t)≥κρH5(t)，且

故整理(4.18)，并利用Gronwall 不等式，得到

定理4.4对任意T ＞0 ，映射(t，z0)→S(t)z0，即 [0，T]×X3→X3是 Lipschitz 连续的，即

对任意的z1，z2∈X3和t1，t2∈ [0，T]，有

证明：证明可详见文献[8].

定理4.5设X3⊂X1是不变紧子集，且X2到X1是紧嵌入，则映射S(t*)：X3→X3有如下分解形式：

且S0和S1满足下列不等式：

证明：对z0∈X3，用S0z0表示方程(1.1)的线性齐次问题的解，则S(t)=S0(t)z0+S1(t)z0，假设z1=分别是以z1=(u10，u11)，z2=(u20，u21)∈X3为初值的解。 令则将分解为

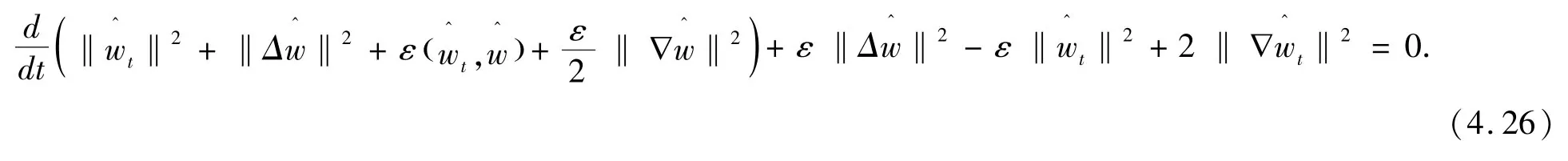
由假设条件

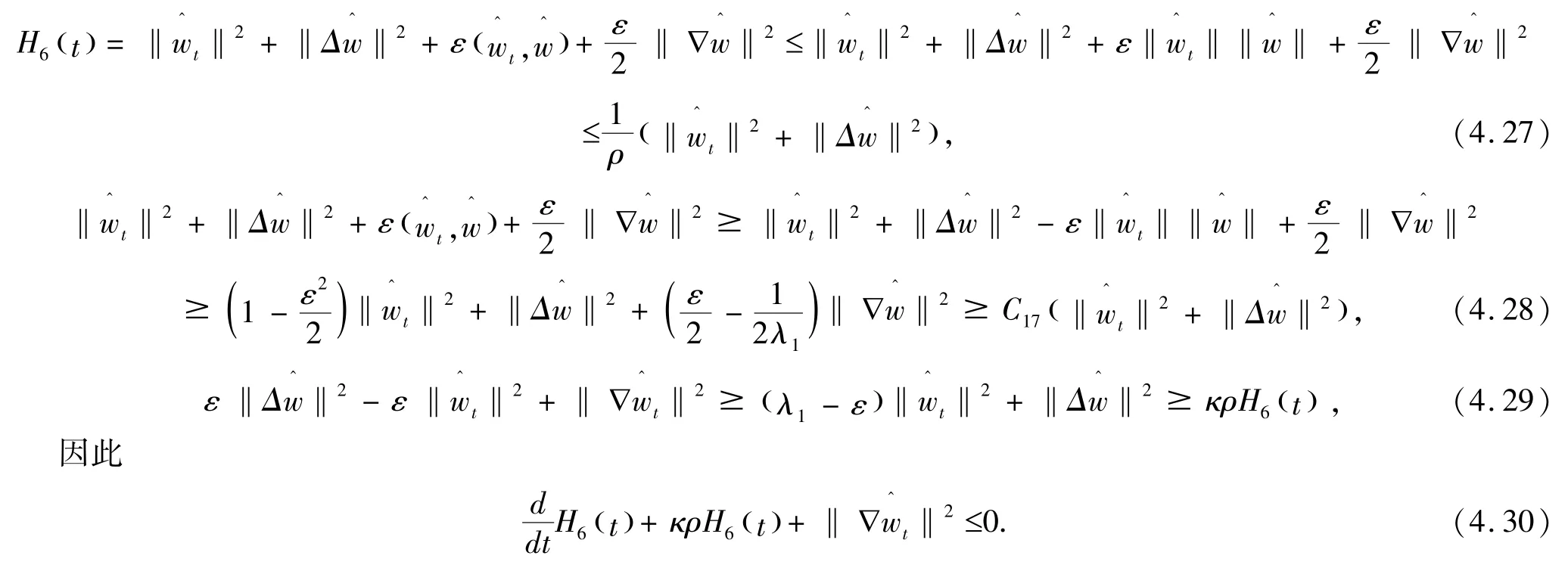
通过(H1) 和gronwall 不等式得到

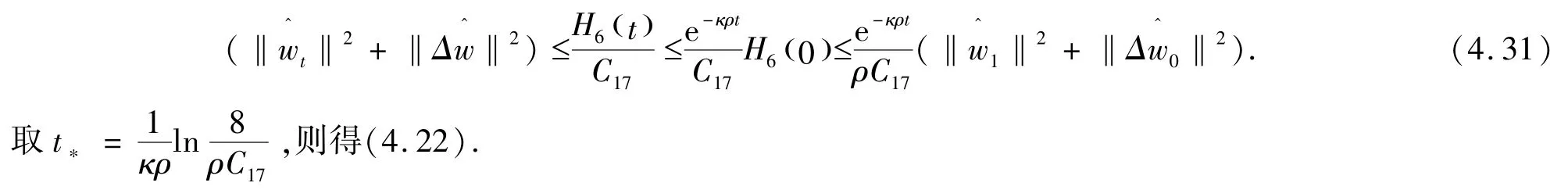
证毕.

由定理2.2，定理4.4 和定理4.5 即可得到下列定理4.6.

定理4.6 (指数吸引子)在满足定理3.1 的假设条件下，则问题(1.1) -(1.3)生成的解半群{S(t)}t≥0在X3上存在指数吸引子.