国际能源价格的持续性结构突变研究

姚青松 赵国庆

摘要：作为生产投入品，不可再生能源对于各国的经济发展具有重要意义。基于多次持续性结构突变检验方法，发现石油与天然气价格均存在两次持续性结构突变，而煤炭价格为一个持续的单位根过程。石油价格在两次世界石油危机后处于非平稳状态，1986年初进入长期平稳区间，并在亚洲金融危机后再一次回到非平稳轨道;天然气价格最初具有较强的平稳性，在2000年初进入非平稳区间，并于2008年末回归平稳过程。此实证检验结果对能源价格平稳性的区间划分具有重要的理论与实证意义，且具有丰富的能源政策意义。

关键词：能源价格;持续性结构突变;单位根;结构变化;石油危机

一、引言

作为生产投入品，不可再生能源对于各国的经济发展具有重要意义，關于能源价格的时间趋势性质以及能源价格波动的宏观经济影响一直是经济学者的研究热点。在现有关于能源价格时间趋势性质的研究中，大量研究尝试基于能源价格的平稳性态对能源价格进行分类，但并未得到一致结论：部分研究支持能源价格的单位根特性（Serletis和Rangel-Ruiz，2004[1];Maslyuk和Smyth，2008[2]），而其他则认为将包括结构变化在内的多种因素纳入研究框架后，能源价格可以被解释为一个平稳过程（Ghoshray和Johonson，2010[3];Narayan和Liu，2015[4]）。

不同于现有研究，笔者尝试实证检验国际能源价格持续性结构突变的存在性。能源价格不能仅基于平稳性进行分类，这是源于一些能源价格的平稳性态往往不具有长期稳定性：其可能在部分时间区间中表现出平稳特性，而在其余区间里呈现显著的非平稳性。上述现象也被称为持续性结构突变（Shift in Persistence）。持续性结构突变问题最早由Kim提出（Kim，2000）[5]，有关持续性结构突变检验方法的文献回顾可以参见Perron（2006）[6]、姚青松等（2019）[7]。在计量经济建模过程中，持续性结构突变对分析结果具有重要影响。Park（2010）[8]指出，当自变量为I（1）过程而因变量为I（0）过程时，回归系数渐近不具有统计显著性，因此当因变量为平稳过程而自变量存在持续性结构突变时，线性回归极有可能支持两者不相关的原假设，即使在平稳区间内自变量对因变量具有显著的影响。姚青松等（2019）[7]证明，对于存在持续性结构突变的序列进行常规单位根检验时（例如ADF单位根检验），当序列的非平稳区间相对较窄，检验结果将在渐近意义上拒绝原假设，支持序列的平稳性，但采用该序列进行线性回归分析可能会导致严重的伪回归问题。在实际应用中，上述问题将扭曲各个宏观变量之间的真实关系，对政策的制定形成错误的导向。在现有研究中，能源价格的宏观经济影响得到非常广泛的关注，其中包括能源价格对于股票市场（Kilian和Park，2009[9];Miller和Ratti，2009[10];Cunado和Perez de Gracia，2014[11]）与外汇市场（Huang和Guo，2007[12];Sari等，2010[13];Wu等，2012[14]）的影响。因此，厘清能源价格的持续性结构突变的存在性并依据平稳性对能源价格进行相应的区间划分具有重要的理论与实证意义。

本文采用Kejriwal等（2013）[15]提出的检验方法（下文简称KPZ检验法）对1980年1月至2019年11月间石油、煤炭以及天然气的月度价格数据进行持续结构突变检验。与现有研究相比，KPZ检验方法具有以下优点。首先，该方法允许存在次数未知的多次平稳性态的转变，相较于仅考虑单次持续性变化的检验过程，该方法具有更高的检验功效。其次，在存在持续结构突变的情况下，该方法允许未知的突变方向（即从平稳过程转变为非平稳过程，或相反），且能够基于检验结果对突变方向进行推断。

研究结果表明，能源价格的持续性结构变化往往伴随着标志性的经济事件，近期研究也支持了该结论（Narayan和Liu，2015[4];姚青松等，2019[7]）。这意味着市场冲击是持续性结构突变的重要推动因素。需要指出的是，持续性结构变化既可能源于供给方或需求方的单方面冲击，也可能源于双方的共同冲击。考虑如下简单的市场供给曲线qtS=aS+bSptS+εtS与需求曲线qtD=aD-bDptD+εtD，其中bS，bD>0，εtS与εtD分别为供给端与需求端的外部冲击。容易解得市场的均衡价格为p*t=（aD-aS）/（bD+bS）+（εtD-εtS）/（bD+bS）。显然，当石油需求端稳定，而石油供给方由于外生冲击转变为单位根过程中，也即εts由I（0）过程转变为I（1）过程，均衡价格p*t由平稳过程转变为单位根过程。此外，供给端与需求端的相互影响也可能进一步放大市场冲击的影响，最终导致非平稳的市场价格。例如，当石油供给端发生冲击，而石油需求端预期该影响可能具有长期持续性，则需求端预期行为的改变会增强市场对于冲击的记忆能力，强化冲击对于市场的影响力。

二、计量模型与检验方法

本文沿用Kejriwal等（2013）[15]所考虑的模型基本思路，假设能源价格序列由如下过程生成：

本文考虑如下两类模型的检验问题：

模型1：当i为奇数时，μi=0，αi=1;当i为偶数时，？琢i<1而μi可以任意取值。

模型2：当i为偶数时，μi=0，αi=1;当i为奇数时，？琢i<1而μi可以任意取值。

显然，在模型1中，数据最初由非平稳过程生成，随后在平稳与非平稳过程之间交替，而模型2则恰恰相反。值得注意的是，模型1与模型2允许截距项在不同的平稳性态稳定区间之间发生变化，但是在区间内具有稳定性。

本文采用Kejriwal等（2013）[15]提出的方法检验多次持续性结构突变的存在性。在该检验方法下，原假设为H0：μi=0且αi=1对所有的i均成立。这意味着在原假设下，yt由持续的单位根过程生成。进一步讨论检验统计量的构建问题。考虑如下的回归方程：

最小二乘方法对回归方程（3）进行估计，并得到原假设下的残差平方和，记作SSR0。进一步考虑备择假设下的模型估计问题。在模型1下，数据首先由非平稳过程生成，随后在平稳与非平稳过程之间转换，因此式（3）对奇数平稳性态稳定区间成立，式（2）对于偶数区间成立;而模型2则相反。在模型1或模型2下，我们基于一个给定的样本分割λ采用最小二乘方法对回归方程进行估计，并得到残差平方和，分别记为SSR1，m（λ）与SSR2，m（λ）。模型1与模型2的Wald检验统计量分别为：

式（4）与（5）均基于某个给定的样本分割λ计算得到，然而在实际应用中我们并不知晓真实结构变化时间与样本分割机制，因此我们进一步考虑sup-Wald统计量：

当上述统计量超过临界值，表明数据存在m次持续性结构变化。此时，可以采用如下的方法对结构突变发生时点进行估计：

最后需要指出的是，上述检验过程可以被进一步扩展至存在时间趋势的时间序列中。在此情况下，需要在式（2）中加入时间趋势项。对于模型1与2的检验统计量可以类似地基于式（4）与式（5）构建得到。在后续讨论中，若不特别指出，我们仅考虑不存在时间趋势的检验。

三、检验结果与分析

（一）数据来源与检验说明

本文所采用的能源价格数据为1980年1月至2019年11月间的石油、煤炭以及天然气价格的月度数据，其中天然气价格的起始月份为1985年1月。本文数据均下载于国际货币基金组织（International Monetary Fund，IMF），所有能源价格数据均采用生产者价格指数PPI进行平减，其中PPI数据来源于美国劳工统计局（U.S. Bureau of Labor Statistics）。平减过后价格数据取自然对数。在检验过程中，考虑到样本容量对于检验结果的影响，我们将m的最大值设定为2，其等价于假设所有能源价格的持续性结构突变至多发生两次。在后续检验过程中，我们将回归方程（2）中差分项的最大滞后阶数设定为：

并采用BIC信息准则基于原假设下的回归结果选择最优的滞后阶数①。

（二）检验结果与分析

1. 检验石油价格序列的持续性结构突变的存在性，检验结果如表1所示。不难看到，在统计量supF11、supF12、supF21以及supF22中，仅统计量supF21在1%的水平上显著。根据Kejriwal等（2013）[15]的结果，当真实过程由模型i生成，然而研究者采用统计量supFjm进行检验时（j≠i），检验结果不再具有一致性（也即supFjm =Op（1））。由于supF21显著而supF22不具有显著性，可以推测石油价格序列可能由模型1生成。在此情况下，石油价格在1980—2019年间发生两次持续性结构突变：其首先由非平稳过程生成，随后进入平稳区间，最终再一次返回非平稳区间。我们进一步采用式（8）估计石油价格的持续性结构突变发生时间，估计结果分别为1985年12月与1997年10月。上述结果表明，1980—1986年，石油价格具有非平稳性;1986—1997年，国际石油价格处于平稳区间;1998年初，石油价格再一次进入长期非平稳震荡之中。

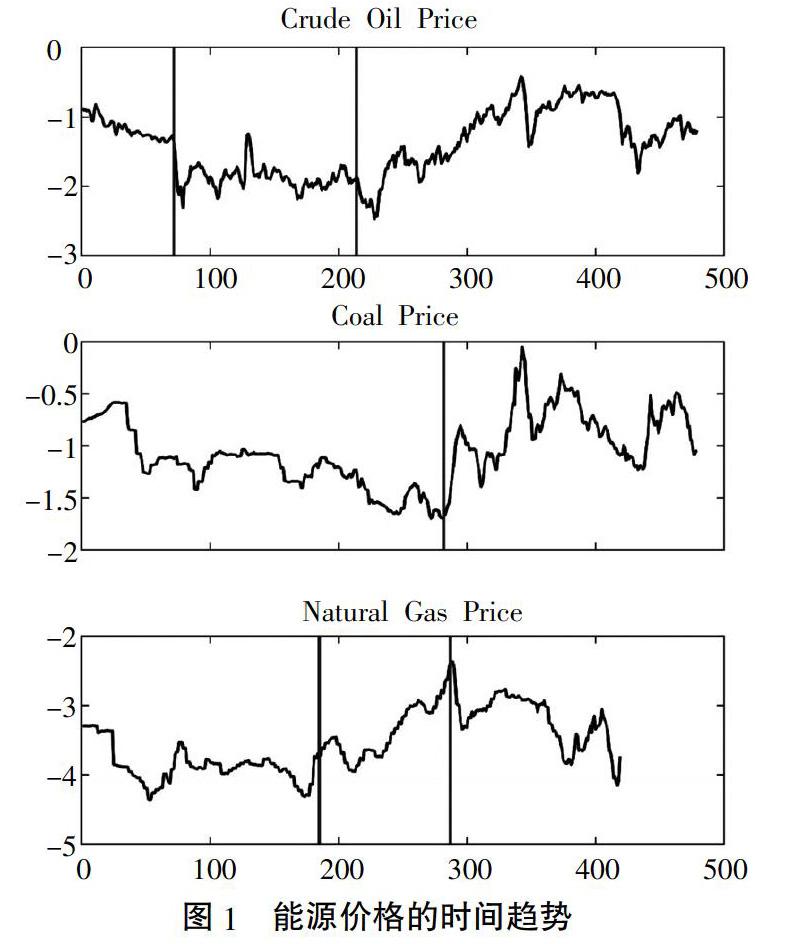
图1展示了1980—2019年石油价格的时间趋势。不难看到，在第一个平稳性态稳定区间内，石油价格呈震荡下降趋势;在第二个区间内，石油价格在低位小幅度波动，具有较强的平稳性;在第三个区间内，石油价格的波动水平显著提高，非平稳性增强。石油价格第一阶段的非平稳性极有可能源于分别发生于1973年以及1979年的两次世界性石油危机。两次石油危机期间，石油价格大幅度上升，这对世界经济造成了巨大冲击，使得OECD国家进入长期的经济衰退之中。石油危机也为石油市场带来了恐慌，进一步加剧了石油市场的不确定性。此外，发生于1980年的两伊战争也增强了石油市场的非平稳性。从图1中可以看到，石油价格自1980年初进入平稳通道。1986年初，沙特阿拉伯放弃配额生产，提高原油产量并大幅度压低石油价格，这使得国际石油价格大幅度下跌，并在低位长期徘徊②。石油价格的第三个平稳性态稳定区间开始于1997年年末，而与此同时，亚洲金融危机爆发。此次金融危机席卷了亚洲重要经济体，使得亚洲经济进入衰退之中。这对石油市场的需求方造成了巨大冲击，石油价格再一次回到单位根过程。

本文进一步对石油价格的检验结果进行稳健性分析。我们注意到在上述KPZ检验过程中假设石油价格不含有时间趋势项，因此首先考察上述假设是否对于检验结果具有显著影响。这里采用Perron-Yabu（2009）[16]提出的检验方法（后文简称PY趋势检验法）检验石油价格在各个区间以及全样本内是否存在显著的时间趋势。PY趋势检验法的主要优势在于，不论误差项为一个平稳过程还是单位根过程，其均能够提供一致的检验结果。表2给出了PY趋势检验结果。不难看到，石油价格仅在第一个区间具有显著的时间趋势。另一方面，本文同时也采用包含趋势项的KPZ检验过程对于石油价格进行检验，检验结果由表3给出。显然，带有趋势项的KPZ检验结果同表1的检验结果基本相同，仅supF21具有统计意义上的显著性，且持续结构突变发生时间的估计结果分别为1985年12月及1992年8月。上述系列结果表明，采用不包含趋势项的KPZ检验得到的结果具有稳健性。

当数据真实过程为一个稳定的平稳过程或存在结构变化的平稳过程时，原假设将在渐近意义上得到拒绝。因此，作为本節的第二个稳健性检验，本文检验石油价格是否为一个平稳过程或带有结构变化的平稳过程。基于KPZ提出的建议，本文首先采用Bai和Perron（1998，后文简称为BP检验）[17]提出的检验方法对回归方程（2）进行结构变化检验，以确定常数项μi以及滞后项yt-1的系数是否具有稳定性;随后，我们进一步采用Ng和Perron（2001，后文简称为NP检验）[18]提出的检验方法以检验石油价格是否至少在一个区间内存在单位根③。当BP检验拒绝原假设时，可以确认μi或αi至少出现一次结构变化，这排除了能源价格为稳定平稳过程的可能性;当NP检验不能拒绝原假设时，可以确认能源价格至少在一个区间内为单位根过程，这排除了石油价格为平稳性结构突变过程的可能性。BP和NP检验结果由表4给出。不难看到，BP检验的UDmax统计量在10%的水平上显著，而NP检验的M族统计量在10%的水平上均不显著。上述结果均表明石油价格不可能为一个平稳过程，这为石油价格的持续性结构突变提供了强有力的佐证。

2. 检验煤炭价格的持续性结构突变的存在性，如表1所示。不难看到，在四个统计量中，仅supF11统计量在10%的水平上显著，该结果表明煤炭价格极有可能存在一次持续性结构突变：其从一个单位根过程转变为一个平稳的价格过程，而结构变化发生时间的估计结果为2003年6月。基于前文的方法，我们利用PY、BP与NP检验对上述检验结果的稳健性进行分析（见表2、表4）。可以看到，对于煤炭价格，不论是全样本还是基于持续性结构突变发生时点划分得到的子样本，PY检验均拒绝了存在显著时间趋势的原假设，这在一定程度上支持了采用无趋势KPZ检验的合理性;然而，BP与NP的检验结果表明，UDmax统计量与M族统计量均在10%的水平上不显著。UDmax统计量的非显著性值得进一步深入讨论，这是因为该结果意味着在公式（2）中，常数项与滞后一期价格的系数均不随时间发生变化。从图1中可以看到，在持续性结构突变发生后，煤炭价格的波动程度进一步升高，这意味着不同于KPZ检验的结果，煤炭价格极有可能是一个持续单位根过程。在此情况下，无趋势KPZ检验结果的伪显著性必然源于BP检验未能检测到的结构变化。为了验证上述分析，本文采用Perron-Yabu结构变化检验（Perron和Yabu，2009）[19]对煤炭价格进行检验。Perron-Yabu结构变化检验的优势在于不论被检验序列是否具有平稳性，检验结果均具有一致性。Perron-Yabu结构变化检验结果表明，ExpW统计量在1%的水平上显著④，这佐证了煤炭价格的均值变化的存在性。事实上，如表3所示，当采用带有趋势项的KPZ检验（允许在原假设与备择假设下存在趋势变化）再一次对煤炭价格进行检验时，不难发现原本显著的supF11统计量不再显著，这进一步表明煤炭价格更有可能发生均值结构变化，而非持续性结构变化。

3. 对天然气价格进行检验。如表1所示，supF22在1%的水平上显著。PY检验结果表明天然气价格仅在第二个区间里存在显著的时间趋势。且根据表3的结果，不论是否包含趋势项，KPZ检验均得到相似的结果。表4中，UDmax统计量在5%的水平上显著而M族统计量均不具有显著性。上述结果表明，天然气价格序列在1986—2019年间存在持续性的结构变化，其在2000年5月从平稳过程转变为单位根过程，而在2008年末再一次回到平稳过程。

四、结论与总结

本文实证检验了国际能源价格持续性结构突变的存在性。研究发现，除了煤炭价格具有持续的非平稳性质外，石油价格与天然气价格均经历了两次持续性结构突变，其中石油价格首先从非平稳过程转变为平稳过程，并最终回到单位根过程，而天然气价格恰恰相反。稳健性检验极大地支持了上述结果。

本文的研究结果具有丰富的政策意义。首先，在能源价格预测方面，本文研究结果表明，石油价格与煤炭价格在2009年后均为单位根过程，这意味着对于煤炭与天然气价格，短期未来价格的最优预测为其当前价格，而长期价格预测则面临极大的不確定性;相反，由于天然气价格在2008年后转变为一个平稳过程，其短期未来价格预测应基于一个平稳ARMA过程，而其长期价格预测则为历史价格的平均水平。其次，不同的能源价格预测机制也表明在能源市场出现波动时，政府应采取不同的应对策略。具体而言，对于石油与煤炭，由于其在近期内处于非平稳区间中，因此市场冲击对于市场的影响具有持续性，因此政府应对能源价格的长期变化做好充足的准备，并充分考量能源价格波动带来的风险;相反，由于天然气价格近期处于平稳区间，因此短期的市场冲击不改变天然气价格的平均水平，政府在中长期决策中依然应以价格的历史平均水平为参考基准。最后，本文的研究结果表明，能源价格的宏观经济影响需要得到进一步的研究。例如，Cunado和Perez de Gracia（2014）[11]利用向量自回归与向量误差修正模型研究了石油价格对于股票市场收益率的影响。为了确保结果的有效性，Cunado和Perez de Gracia在模型估计前首先对数据进行系列单位根检验，并得到所有序列具有单位根的结论。由于传统意义上的单位根检验难以发现持续性结构突变的存在，因此这将严重影响回归分析结果的可靠性。

本文的研究内容还存在进一步的扩展空间。如引言中所述，能源价格市场的供给端与需求端冲击均会对能源价格的平稳性态产生的影响，因此，如何基于宏观数据分析持续性结构突变的来源并对冲击的因素进行分解值得进一步深入研究。

注释：

①有关最大滞后阶数以及最优滞后阶数的选择问题，可以参见Perron在其主页提供的Matlab与Gauss程序代码（http：//people.bu.edu/perron/）。

②石油价格在1990年海湾战争期间出现过短期增长，但随后再一次回到低位。

③基于KPZ的建议，在进行NP单位根检验时，应采用MAIC进行最优滞后阶数的选择。

④不论是否考虑趋势项，该检验结果均成立。

参考文献：

[1]Serletis A， Rangel-Ruiz R. Testing for common features in north American energy markets[J]. Energy Economics，2004（3）：401-414.

[2]Maslyuk S， Smyth R. Unit root properties of crude oil spot and futures prices[J]. Energy Policy，2008（7）：2591-2600.

[3]Ghoshray A， Johnson B. Trends in world energy prices[J]. Energy Economics，2010（5）：1147-1156.

[4]Narayan P K， Liu R. A unit root model for trending time-series energy variables[J]. Energy Economics，2015（50）：391-402.