水库异重流的三维数值模拟及影响因素分析

章若茵，吴保生

（清华大学 水沙科学与水利水电工程国家重点实验室，北京 100084）

1 研究背景

异重流是两种比重相差不大的流体，因为比重差异而发生的相对运动。浑水入库形成的泥沙异重流是水库中常见的现象，其潜入过程以及流速与含沙量沿垂向的分布规律等是水库异重流研究的重要内容，对优化水库调度、提高水库运用效益具有重要意义。但由于异重流潜入区域的变动以及异重流沿库底流动的特点，在天然水库中观测完整的异重流潜入以及流速和含沙量的垂线分布较为困难，前人多以水槽试验或数值模拟的结果来探讨其分布的规律。

范家骅［1］、芦田和男［2］、曹如轩等［3］、方春明等［4］、焦恩泽［5］、李涛等［6］通过水槽试验、水力分析和数值计算等手段对不同比降、不同粒径、不同水沙条件下的异重流潜入进行研究，分析了潜入点Froude 数的大小以及潜入水深与流量、含沙量、底坡的关系。但多数只分析了潜入水深与潜入点所在位置的流速、含沙量关系，而董炳江等［7］利用进口密度Froude 数表征入口水流的惯性力与浮力作用之比，受到入口流量和含沙量的影响，并根据数值模拟结果得到潜入水深与进口水深之比会随着入口Froude 数的增加而增加的认识。这一变化趋势虽然在前人［8］根据实测资料、水槽试验和数值模型得到的结论范围内，但缺乏定量描述，且入口Froude 数变化在0.5 ～8 的范围内，当入口Froude 数在更大范围内变化时这一关系是否存在仍不确定。

异重流潜入后的流速和含沙量分布与明渠水流完全不同，异重流的流速分布中存在最大流速点，一般认为其在异重流高度的0.2 ～0.3 倍之间，这与异重流水沙交界面的确定方法有关，也与床面粗糙程度有关，当床面粗糙程度大时最大流速点的位置会提高，因为受到下边界的阻力作用增强［9］。而含沙量的分布较为复杂，垂直分布与否及垂直分布的厚度等与泥沙粒径、浓度以及冲淤状态均有关系，并没有较为一致的结论。焦恩泽［10］认为交界面以下的流速分布近乎对数分布，而含沙量在一般含沙和高含沙量时有不同的分布型式。Peakall 等［11］、Kneller 等［9］列举了高含沙量、低含沙量、冲刷状态以及非均匀沙情况下4 种不同形式的异重流含沙量分布。Lee 等［12］根据水槽试验结果认为无论是急流还是缓流情况，异重流的流速和含沙量的分布都较一致，与水沙条件无关，但由于只在每组试验中观测了两个断面，断面Froude 数只在1.05 ～1.40 范围内，此结论存在局限性。而Sequeiros［13］认为异重流流速和含沙量的分布与水沙条件、床面形态等均有关，当断面Froude 数减小时，最大流速的位置提高，含沙量在靠近河床处垂直分布的区间更厚，其Froude 数变化范围在0.41 ～2.21 之间。由此可见，对于异重流流速和含沙量分布随水沙条件的变化规律仍然存在一定的争议，值得进一步研究。

本文选择SCHISM 模型对Lee 和Yu［12］的水槽试验进行三维数值模拟，不仅能表现异重流强烈的三维特性，明显优于以往采用一维模型［14］和立面二维模型［15］对此进行的模拟，而且能根据三维模拟结果分析不同时间和断面的异重流运动情况，补充原试验分析的不足。SCHISM 是基于雷诺时均方程（RANS）的三维数值模型［16-18］，相比于直接数值模拟（DNS）和大涡模拟（LES）等仅适用于实验室尺度的模型，SCHISM 能够应用于实验室和实际工程等各个尺度的模拟。SCHISM 在水平方向上采用无结构化网格，能够灵活适应复杂的边界条件，优于FLOW-3D 等模型中的结构化网格［19］；垂直上则包括SZ坐标［20］和LSC2坐标［21］两种方式，两种方式均有良好的垂向边界跟随性，其中SZ 坐标结合了z 坐标和张芝永等［22］、Pérez-Díaz 等［23］在三维模型中采用的σ坐标，一定程度上消除了σ坐标在底坡突变的情况时产生的不合理的跨密度面混合和压力梯度误差，同时LSC2坐标也可消除这种误差［24］，因此均适合运用于发生在底坡陡降、水深突增情况下的水库异重流。此外，在引用隐式TVD2格式计算物质运输后，SCHISM 在模拟盐水入侵、密度分层等现象时更加精确［25-26］。但目前来看，SCHISM 模型多用于河口处盐度或温度异重流模拟，而缺乏模拟水库泥沙异重流的研究。

本文将首先通过对水库异重流水槽试验的模拟，验证该模型模拟水库异重流的可靠性和准确性；然后根据模拟结果，分析不同入口水沙条件下异重流潜入点的变化规律和潜入后含沙量、流速分布的规律，探讨入口水沙条件与潜入水深之间的定量关系。研究结果不仅为下一步运用SCHISM 模型模拟大型水库泥沙异重流奠定基础，而且加深了对异重流水沙运动和分布规律的认识。

2 三维水沙数学模型

2.1 控制方程与湍流模型SCHSIM 模型基于RANS 方程，并且满足静压假定和Boussinesq 涡黏性假定，其在笛卡尔坐标下的控制方程如下：

连续方程：

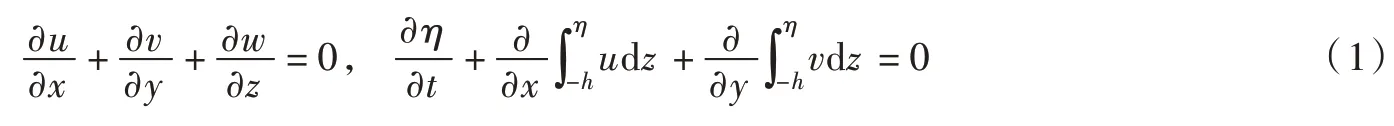
动量方程：

物质输移方程：

状态方程：

式中：x、y 为水平笛卡尔坐标，m；z 为垂向坐标，向上为正，m；u、v、w 分别为x、y、z 三个方向的流速，m/s；t 为时间，s；h 为水深，m；η为自由水面水位，m；f 为柯氏力系数，s-1；ρ0、ρ分别为参考密度和水体的密度，kg/m3；g 为重力加速度，m/s2；Kmh、Kmv分别为水平与垂直涡黏性系数，m2/s；pA为自由水面的大气压强，N/m-2；C 为物质浓度，此处为含沙量SSC，kg/m3；ωs为泥沙颗粒沉速，m/s；Ksh、Ksv分别为水平和垂直方向的泥沙扩散系数，m2/s；q 为输运物质的源汇项。

式（1）—式（3）采用有限元和有限体积法进行求解，式（4）采用有限体积法求解。当式（4）用于计算其他变量（盐度S/PSU、温度T/℃等）时，则没有泥沙沉速这一项。本文中暂时只考虑泥沙造成的异重流现象，因此模型中的盐度设置为0，而入流水体和环境水体的温度保持一致。

为了求解式（1）—式（4）需要采用湍流模型闭合，模型中采用Umlauf 和Burchard［27］的通用长度模型GLS（Generic Length-scale model），包括紊动能K 和通用长度变量ψ的控制方程，其中通用长度ψ由下式定义：

2.2 边界条件针对式（2）—式（3），水面上不考虑风应力的影响时，水平流速的垂向梯度为0；床面上根据水体底层的雷诺应力与床面摩擦剪应力的平衡关系给出：

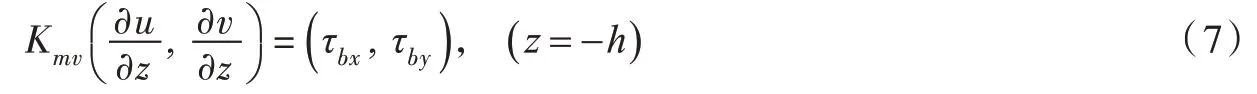
式中τbx、τby为床面的摩擦剪应力，m2/s2，由湍流边界层和阻力系数确定［31］。对式（4）水面和床面上的边界条件为：

式中：Cb为床面含沙量，kg/m3，可根据文献［32］的方法计算；α*为非平衡输沙响应系数，表示床面含沙量与垂向平均含沙量之比，可随水沙条件动态调整；S*为垂向平均挟沙力，kg/m3。与方程（9）相对应的河床变形方程为：

式中：ρ′为河床组成物质的干密度，kg/m3；Z 为床面厚度，m。

3 水槽异重流试验模拟

3.1 水槽试验条件为了研究异重流潜入后垂向上流速和含沙量分布的特点，Lee 和Yu［12］针对水库异重流进行了一系列水槽试验。试验所用的水槽长20 m，宽0.2 m，坡度为0.02，通过设置出口水位保持明渠段长4 m，壅水段长16 m，以及斜坡尾部的蓄水池长1 m，其侧面示意图和高程如图1 所示。选用的泥沙是粒径为0.0068 mm 的均匀沙，粒径较细，泥沙比重2.65。

选择水槽试验中的TC01—TC18 组进行模拟，每组试验的入流水沙条件、温度如表1。不同的入口水沙条件可用进口密度Froude 数来表示：

式中：Fr0为入口密度Froude 数；U0、h0和q0分别为入口的流速、水深和单宽流量；g′为有效重力；Δρ为入口浑水（ρin）与清水（ρa）的密度差，各组对应的Fr0数也列于表1。

图1 水槽设置示意图及网格高程

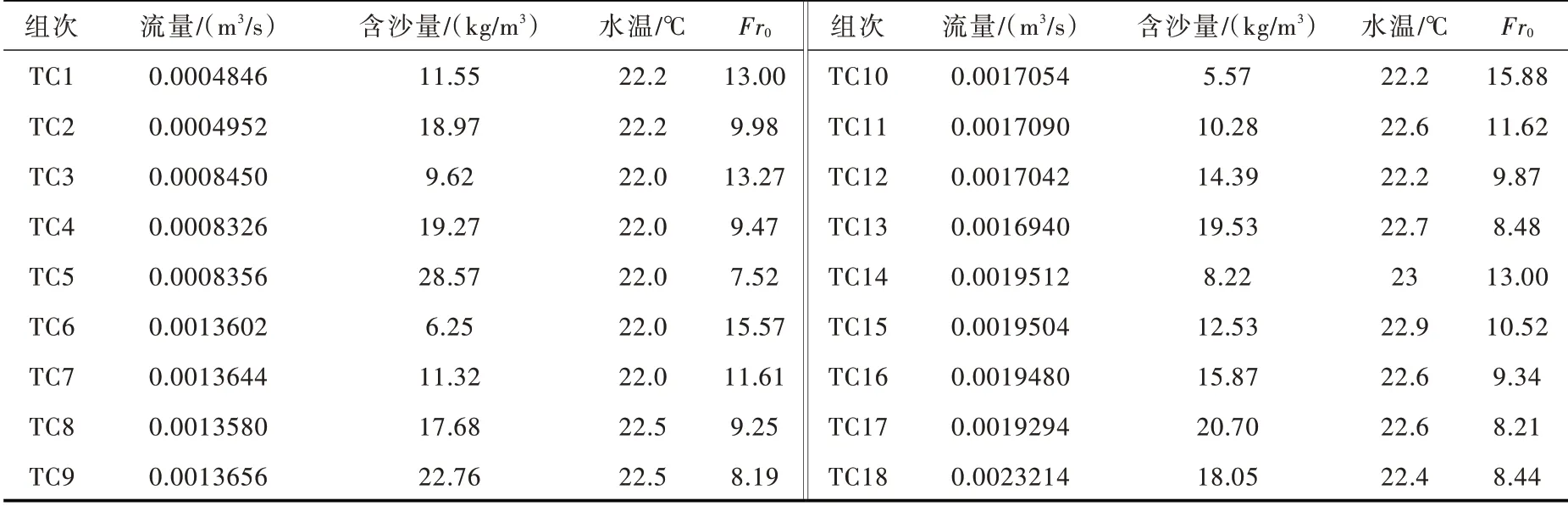
表1 TC01—TC18 组水槽试验入库水沙条件

3.2 模型设置与选择考虑到矩形水槽较为规则，本文在水平向采用四边形网格，尺度为2.5 cm×2 cm，则网格数8400，节点数8251。模拟时间步长为0.1 s，每1 s 输出结果，模拟时长810 s。选用清华大学“探索100”集群进行计算，由于模拟尺度较小，每次计算使用12 个核［33］。由于垂直分层的方式和层数对于数值模拟的计算精度影响较大，所以根据SCHISM 两种垂向网格方式，设置3 种不同的垂直分层方式如表2 所示，分别模拟TC14 组的异重流过程，从而确定最终的垂直分层方法。

表2 不同垂直分层方法的层数要求

本文以垂线上流速为0 的点为清浑水交界面的位置，则TC14 组交界面以下实测及模拟的流速和含沙量分布如图2 所示，沿程含沙量分布如图3 所示。由图2（a）可知，3 组模拟的流速分布均出现了最大流速点，且最大流速点上、下区域的流速分布规律不同。A 组模拟的流速分布与实测情况最为吻合，在距水槽底部4.8 cm 处达到最大流速点10.32 cm/s，略大于实测的10.27 cm/s；B 组最大流速点的位置在距底3.8 cm 处达到10.05 cm/s，但最大流速点以下的部分与实测点相差较大；C 组的流速分布明显与实测分布差别较大。由图2（a）可以看到，实测最大流速点以下只有一个实测数据点，为了弥补实测数据点较少的问题，利用Geza 和Bogich［34］提出的异重流最大流速点以下的流速分布公式进行了补充计算，其具体计算公式如下：

式中：ue为高度z 处对应的流速；u′em为最大流速；h1e为最大流速点到河底距离； u*为摩阻流速；κ为卡门常数，与最大流速点以下的平均流速有关，经计算此处为0.27。

根据式（12）得到异重流最大流速点以下的流速分布曲线，见图2（a）。可以看到，理论公式曲线具有与A 组相近的分布，说明采用A 组模拟的流速分布是较为可靠的。需要说明的是，根据边界无滑动条件假定，垂向流速在河底处均为0，而文中所有的流速分布均只绘制到河底上一层流速，因此并不为0。

图2 不同垂直分层方法模拟的流速和含沙量分布（TC14）

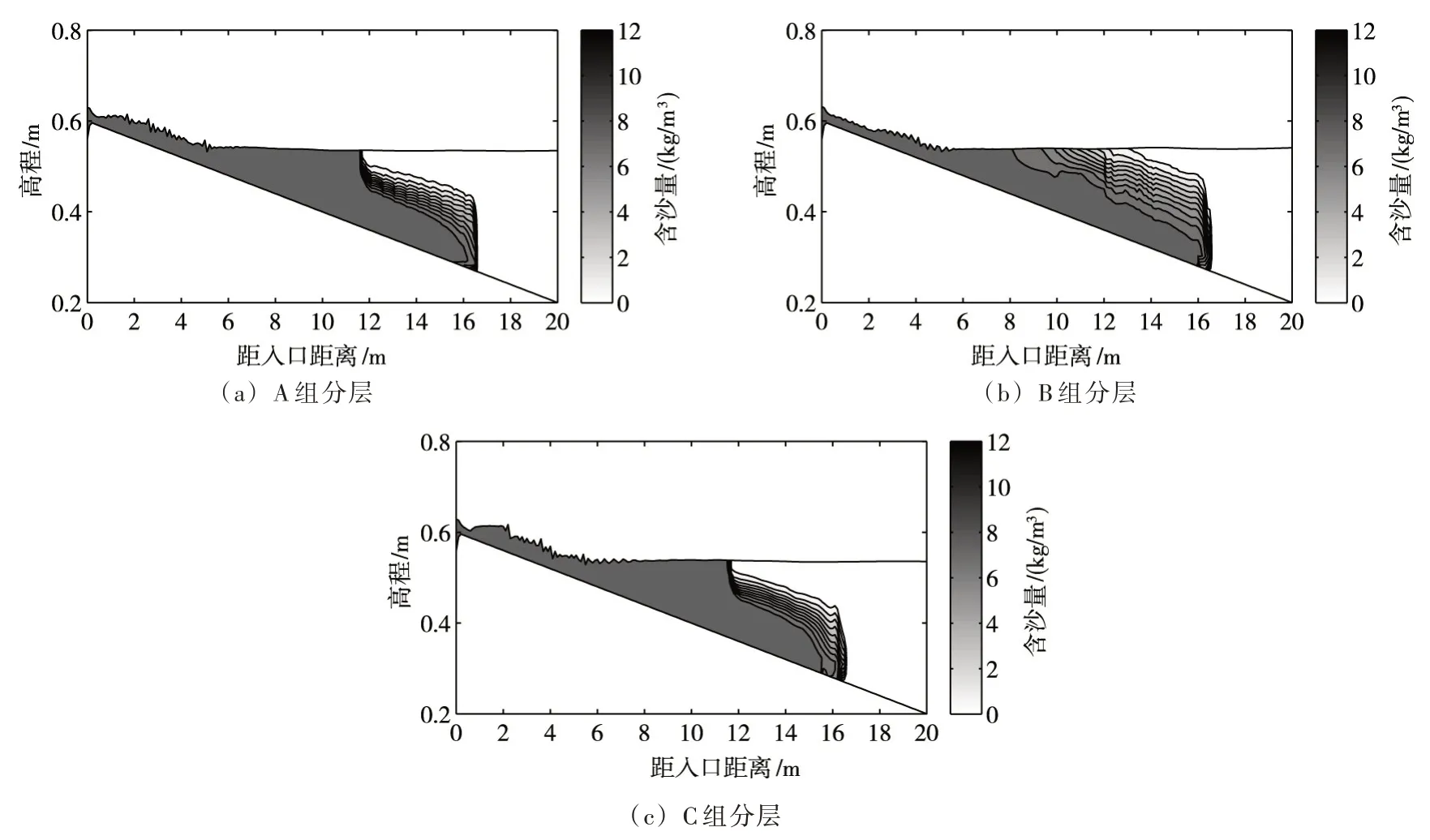
图3 不同垂直分层方法模拟的TC14 组沿程含沙量分布（t=150 s）

由图2（b）可知，A 组和C 组的含沙量与实测分布较为接近，含沙量在交界面以下迅速变大，且在靠近底部的一定厚度呈现垂直分布的情况，与三门峡水库实测高含沙量异重流的含沙量垂线分布十分相似，主要是由于颗粒较细、含沙量较高产生的黏性作用，导致含沙量呈现几乎垂直分布的特点［10］，一般称这个垂直分布的区间为致密层。而B 组的含沙量分布明显较为均匀，图3（b）的沿程含沙量分布没有明显的异重流潜入点，这可能是因为垂向分层过少导致模型计算时垂向扩散剧烈，异重流潜入过程不明显。综合流速和含沙量分布来看，A 组的分层方法具有较明显的优势，因此最终选择A 组方式进行其余组次的模拟。

3.3 模型验证采用上述配置模拟TC01—TC18 组水槽试验后，以TC14 组为例，浑水进入壅水段后形成异重流并稳定运动的完整过程如图4 所示。浑水从明渠段进入壅水区后，会在满足异重流潜入条件的位置处下潜形成异重流。图中显示约40 s 时，接近河床位置的含沙量变大，而表层含沙量较小。异重流有开始向下潜入的趋势，随着时间变化，异重流潜入的位置逐渐向下游移动，直到一个固定的位置，形成稳定的异重流潜入点［35-36］。图5 是160 s 时潜入点附近的流场分布图，可以看到，异重流潜入点及清浑水交界面处流速接近为0，而上层清水流速较小，且有反向流速，同时异重流内部的流速都较大。

为了分析异重流潜入以后垂线上流速和含沙量的分布特点，可提取潜入点下游断面垂线上的流速和含沙量，根据式（13）得到该垂线上的异重流平均厚度、平均流速和平均含沙量［37］：

图4 异重流潜入及运动时的沿程含沙量分布（TC14）

图5 潜入点附近流速（t=160s）

式中：U 为不同高度的流速；Ugc为异重流平均流速；hgc为异重流平均厚度；C 为不同高度的含沙量； Cgc为异重流平均含沙量；δ表示垂线上流速为0 的位置与水槽底部之间的距离。

利用计算的异重流厚度hgc、平均流速Ugc和平均含沙量Cgc代入式（11）可以得到此时该断面上异重流的Froude 数Frd。

原试验在潜入点下游测量并计算了两个断面的相关数据，本文从模拟结果选取相同断面的流速和含沙量得到hgc、Ugc和Cgc，实测与模拟结果的对比如图6 所示。由图6 可知，hgc、Ugc和Cgc的R2分别为0.95、0.92 和0.94，三者的符合程度都较高，说明SCHISM 模拟的异重流潜入后的运动过程与实测过程较为一致，模拟结果基本可靠。

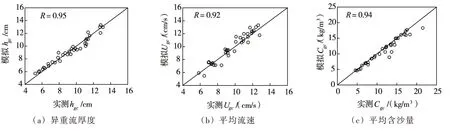
图6 实测与模拟异重流平均流速、厚度和平均含沙量对比（TC01—TC18）

4 异重流影响因素分析

4.1 入口含沙量的影响由表1 中TC14—TC17 的入流水沙条件可知，这4 组流量接近，但入流的含沙量逐渐增加，可以对比分析入流含沙量对异重流流速和含沙量分布的影响。因160 s 时异重流运动受到水槽尾部的回流影响较小，所以以该时刻距入口14 m 的断面为例，据式（11）和式（13）计算不同组次的hgc、Ugc、Cgc和对应的Frd数列于表3，该时刻沿程的含沙量分布如图7，分别以表3 中的hgc、Ugc和Cgc为参考值，可以得到在交界面以下流速和含沙量随深度的无量纲分布，见图8。

表3 不同入流含沙量对异重流的影响

图7 入口含沙量不同时异重流的含沙量沿程分布（t=160 s）

由表3 和图7 可知，不同的入口含沙量导致异重流的运动速度不同，含沙量越大，浑水与环境水体的密度差增大，异重流头部的能量与动量越大，则异重流运动速度越快，14 m 断面上的平均流速从0.090 m/s 增长到0.131 m/s。但同样环境水体形成的反向流速也较大，对异重流的压力增大，异重流环境水体的内外压力差增大，导致异重流厚度越小，TC14 时该断面的异重流平均厚度达0.145 m，而TC17 中平均厚度只有0.102 m，与图7 中的分布一致，也与谢鉴衡［38］、董炳江等［7］的结论一致。此外，从图7 还能看出同一时刻，入口含沙量越大，则异重流潜入点的位置越向上游，潜入水深越小。异重流潜入以后，基本保持一个较为稳定的厚度持续向下游运动，但是头部的厚度略大，主体部分的厚度则略小。

图8 不同入口含沙量条件的无量纲化流速和含沙量分布

结合表3 中的Frd数和图8 中的无量纲化的流速和含沙量分布来看，这4 组的Frd数从1.15 增长到1.28，流速和含沙量的分布有区别但不明显，可能是因为Frd数的增长幅度较小。最大流速点的相对位置在0.38 ～0.42 附近波动，而最大流速从Ugc的1.20 倍增长到1.23 倍；致密层的厚度从hgc的0.47 倍降低到0.3 倍，对应的含沙量则从Cgc的1.15 倍增加到1.22 倍。虽然存在波动，但从变化趋势来看，最大流速和致密层的含沙量均会随Frd数的增大而增大，而最大流速点的位置和致密层厚度则会随Frd数的增大而减小，且含沙量的变化比流速的变化更敏感。较大的Frd数说明水流惯性更大，则水流持续向下运动的能力越强，最大流速点越低。

4.2 入口流量的影响表1 中TC02、TC04、TC13 和TC18 组的流量逐渐增加，而含沙量接近，因此对比这4 组的结果可以分析入库流量对异重流的影响。由于入流流量不同，这4 组异重流前进速度相差较大，因此保证异重流前峰运动到大致相同的位置时，每组的时间不同，分别选取该4 组试验在268 s、213 s、154 s 和136 s 时断面14 m 的结果，不同组次的异重流厚度、平均流速、平均含沙量和对应的Frd数列于表4，沿程的含沙量分布如图9，分别以表4 中的hgc、Ugc和Cgc为参考值得到的流速和含沙量无量纲分布如图10 所示。

表4 不同入库流量对异重流的影响

图9 入口流量不同时异重流的含沙量沿程分布

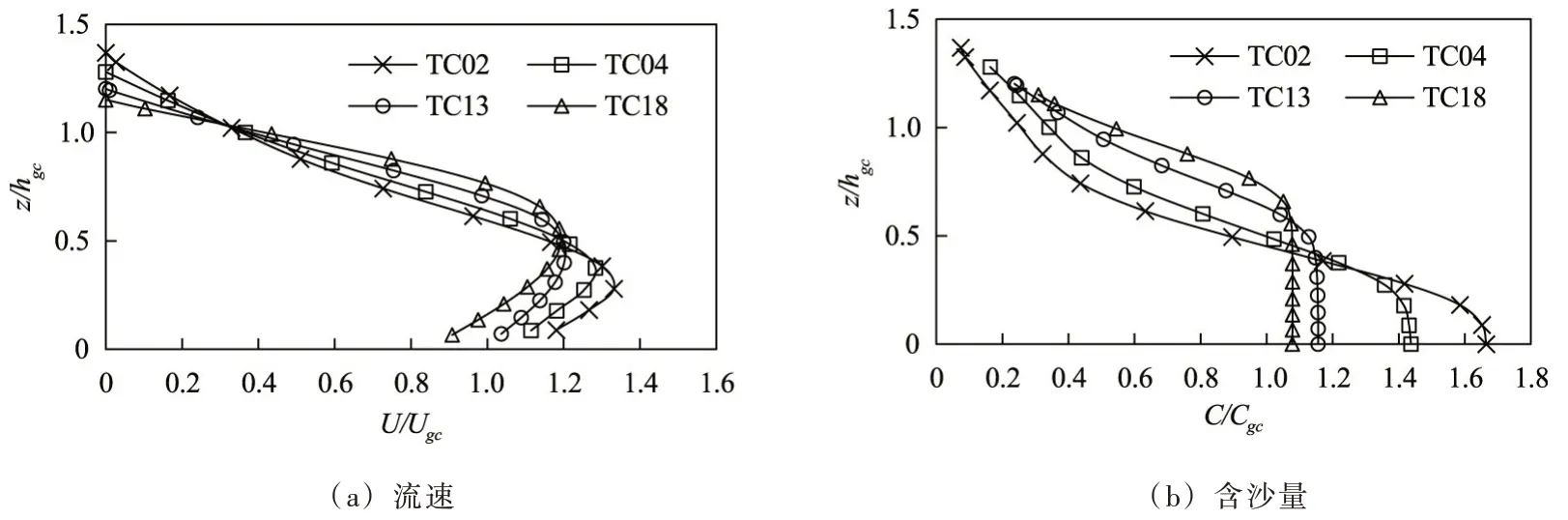
图10 不同入口流量条件的无量纲化流速和含沙量分布

由表4 和图9 可知，入库流量越大，则异重流潜入位置越向下游移动，潜入水深越大，这也与前人发现的规律一致［4］。并且入流流量越大，动能越大，异重流厚度越大，平均厚度从0.079 m 增加到0.101 m，异重流前进速度也越大，平均流速从0.081 m/s 增加到0.103 m/s，但是TC18 的平均流速较小，这可能是由于该组异重流潜入点距入口较远，异重流尚未充分发展至较稳定的状态即到达水槽尾部，因此14 m 处的水沙状态可能受到异重流头部强烈紊动作用的影响，而前三组的14 m 处基本已经处于异重流主体较稳定的状态，因此TC18 组的结果不一定符合规律。

结合表4 中的Frd数和图10 中的无量纲化流速和含沙量分布可知，如TC02 的Frd数较大为1.22，则最大流速点位置低，只达到hgc的0.28 倍，而最大流速为Ugc的1.33 倍，致密层的相对厚度越小，甚至在接近床底时才达到最大含沙量，但最大含沙量能达到Cgc的1.66 倍；而TC18 的Frd数为0.85，最大流速点能够达到hgc的0.46 倍，而最大流速减小为Ugc的1.19 倍，致密层的相对厚度可达0.66，而致密层的含沙量则只有Cgc的1.05 倍。

4.3 Froude 数对异重流潜入的影响前文分别分析了入口的流量和含沙量对异重流潜入位置的影响，两者的影响各不相同。下面以入口的Fr0数作为特征量综合考虑入口水沙条件对潜入点造成的影响。

分析各组的异重流潜入位置、式（11）和表1 可知，入口含沙量越大时对应的Fr0数越小，而入口流量越大时对应的Fr0数越小，后者看似与式（11）矛盾，实际上若保持入口水深h0不变，则入口流量增加会导致Fr0数增加，但由于本文的模拟中没有保持入口水深h0的不变，因此入口流量增加的同时会造成h0变大，而h0的增加又会造成Fr0数的减小，因此综合考虑入口流量和水深的影响后，发现入口流量的增加最终会减小Fr0数。入口含沙量和流量的增加都会导致Fr0的减小，但前者导致潜入水深Hps减小，后者却导致Hps增加，这种矛盾可能是由于h0对Fr0数的影响大于流量的影响产生的。考虑到Fr0数为无量纲数，则以潜入水深和入口水深的比值Hps/h0作为无量纲参数，根据本文18 组模拟结果得到图11 所示Hps/h0与Fr0的关系，可用式（14）来表示，且R2能够达到0.90：

图11 Hps/h0与入口Froude 数关系

图11 还给出了前人所得Hps/h0与Fr0的关系［8］，虽然它们分别表示水槽试验、数值模拟或现场实测等不同环境中的异重流，且底坡不同、入口水沙条件不同或产生异重流的原因不同，如温度、盐度异重流等，但是Hps/h0与Fr0始终遵循幂函数相关的关系，且本文结果在入口Froude 数大于8 时仍然满足这一关系，说明这一关系在异重流运动中是普遍存在的，即可以率定式（14）在不同异重流的参数后根据入口流量、水深和含沙量确定异重流潜入的位置。但是是否存在一个普遍适用的统一公式可以包括不同情况的异重流仍需要更多的数据进行验证和进一步的研究。

5 结论

（1）本文采用SCHISM 三维水沙数学模型模拟了水槽异重流试验，选择LSC2的垂直分层方法以及最多51 层的层数保证异重流模拟的精度及效率。模拟结果与实测异重流平均厚度、平均流速和平均含沙量吻合较好，对应R2均能达到0.9 以上，同时潜入点下游断面的流速和含沙量的垂线分布也符合实测的分布情况。

（2）异重流潜入后的运动和水沙分布规律与入口水沙条件相关，入口含沙量越大，异重流运动速度越快，厚度越小；入口流量越大，异重流运动速度越快，厚度越大。流速和含沙量的无量纲分布与断面Froude 数密切相关，断面Froude 数从0.85 增长到1.22 时，最大流速从1.19 增长到1.33 倍平均流速，致密层含沙量从1.05 增长到1.66 倍平均含沙量，而最大流速点与河床距离从0.46 减少为0.28倍平均厚度，同时致密层厚度从0.66 倍平均厚度减小为0。

（3）异重流潜入点的变化与入口水沙条件相关，入口含沙量越大，入口流量越小，则异重流潜入位置越向上游，潜入水深越小。潜入水深与进口水深的比值Hps/h0随入口Froude 数的增加而增加，建立了两者之间的幂函数关系，可以用于确定异重流潜入点的水深。但是否存在一个普遍适用的统一公式来描述不同异重流的情况还需要进一步研究，为推广到实际水库中预测潜入点的水深和位置提供依据。