离心模型试验中界面土压力盒标定方法研究
2020-07-27蔡正银代志宇徐光明任国锋
蔡正银,代志宇,徐光明,任国锋
(南京水利科学研究院 岩土工程研究所,江苏 南京 210024)
1 研究背景
在岩土工程领域,离心模型试验产生的超重力场可以真实有效地还原结构和砂土的受力状态,同时,使用微型界面土压力盒可以量测土与结构接触面处土压力的变化情况。但试验过程中砂土的受力变形特性往往比较复杂,若要准确量测土压力,首要前提就是采取合理的方法得到土压力盒的标定系数。由于传感器本身是由众多微小的电子元件组成,工作状态必然受传感器尺寸、宽厚比、材料刚度、环境因素等的影响,对此国内外学者进行了广泛而深入的研究。
Dave 等[1]通过单向加压的方法,研究了不同厚度砂土中土压力盒的响应问题,并将试验结果与水标试验结果作了对比。Wachman 等[2]也是通过单向加压的方式,研究了非均匀荷载下土压力盒的非线性响应问题。Madabhushi 等[3]通过气囊加压的方式研究砂土介质中土压力盒的标定方法,结果发现,当土颗粒粒径增加时,土压力盒输出数据与加压水平曲线偏离零点的范围也会加剧,这说明不同的颗粒材料组成会影响土压力盒的测量结果。Weiler 等[4]对土压力盒宽厚比展开研究,结果发现土压力盒厚径比越小,土压力测量越准确。Daigle 等[5]提出在土压力测量中,当土压力盒的量程选择不当时,温度对土压力盒的测量精度影响较大。徐光明等[6]通过总结前人经验开发出一种适用于超重力场中土压力测量的传感器,并使用离心模型试验验证了该传感器测量的可行性。芮瑞等[7]对砂土介质中的土压力盒进行了1 组加载标定和4 组卸载标定后发现,加载曲线线性较好,而卸载曲线可采用指数曲线来进行拟合。曾辉等[8]通过数值计算和试验研究,揭示了传感器安置误差对匹配系数和传感器周围应力场的影响规律,提出了界面土压力盒的设计原则和安装埋置要求。焦志斌等[9]开展了土压力测试现场试验,使用土压力盒测试了深水板桩结构静止土压力系数,以及前板桩墙两侧土压力变化规律。
目前,在常规试验中,有关土压力盒标定的研究已日趋完备,但随着土工试验测试技术的发展,土工离心机在岩土工程测试中的应用越来越广泛。与常规试验相比,由于离心机测试设备和数据采集设备工作环境的特殊性,导致界面土压力盒在超重力场中的测试状态比较复杂。本文通过离心模型试验,从考虑外界温度变化,土压力盒上覆砂层厚度和颗粒粒径变化对土压力盒标定结果影响的角度展开研究,以提高超重力场中界面土压力测量的准确性。
2 试验材料与方法
2.1 试验设备本试验在南京水利科学研究院60 g·t土工离心机上进行。该离心机的有效半径为2 m,最大载荷(模型箱+模型):100 g 时,600 kg;200 g 时,300 kg。加速度控制采用可控硅无级调速方式。该机配有60 个银质滑环通道用于信号传输,可满足应力、应变、弯矩、位移等多种物理量的测量需求。
2.2 试验土样试验砂土采用福建标准砂,3种土样按照粒径从小到大按编号分别为1#砂、2#砂和3#砂,根据土工试验方法标准[10],得到1#砂最小干密度为1.40 g/cm3,最大干密度为1.60 g/cm3;2#砂最小干密度为1.43 g/cm3,最大干密度为1.64 g/cm3;3#砂为最小干密度为1.46 g/cm3,最大干密度为1.71 g/cm3。颗粒组成如表1所示。

表1 土样颗粒组成
2.3 砂雨法制备土样利用砂雨法对砂土制样可以有效保证试样密度的均匀性,但在试验前需要首先考虑相对密度Dr 随落距、出砂孔型式的变化规律,分析Dr 空间均匀分布特征。Madabhushi 等[11]和马险峰等[12]在砂雨法制样中考虑了出砂头的孔径大小、出砂量、出砂头水平移动速度对相对密度的影响,并展开了详细研究。本试验分别使用鸭嘴式和网眼式出砂口(图1 所示),其中1 号鸭嘴式出砂口宽度为5 mm,2 号和3 号网眼式出砂口网眼直径分别为3 mm 和5 mm,分别对应3#砂、1#砂和2#砂的制样过程。然后通过自制的砂雨法制样设备进行试验,将不同的砂土均匀撒入至标定罐中,控制落距分别为20、30、40、50、60、70、80、90 和100 cm,每撒砂2 cm 升高一次撒砂口。撒砂过程中使出砂口移动速度缓慢均匀,撒砂完毕后通过称量标定罐与砂样质量来计算砂样密度。最后得到落距和试样密度的关系。其中,标定罐内径为21.1 cm,高为11 cm,净重3.7 kg。

图1 出砂口与标定罐
2.4 土压力传感器标定
2.4.1 不同水温下的水标试验 本试验选择BW-3 型土压力盒,技术参数参考徐光明等[6]的详细研究。在水标前要先对空载情况下超重力场对土压力盒测量结果的影响进行试验,首先将土压力盒粘贴在不锈钢金属板上制作的凹槽中,粘贴时确保土压力盒平面与不锈钢板平面齐平,并确保传感器在受力时不发生变位,传感器布设如图2 所示。之后将预制的不锈钢板平放于模型箱(700 mm×350 mm×450 mm)底部,最后将模型箱吊入到NHRI 60 g·t 离心机中,控制离心加速度为50 g 进行试验,离心机在每级加速度下稳定10 min,进行土压力盒空载标定试验。当离心机开启后,放有模型箱的吊篮被甩起,镶嵌有土压力盒的不锈钢金属板正对离心机旋转中心,这时各土压力盒所受离心力相等。试验结束后,按照同样的方法进行水标试验,分级控制加速度为10 g、25 g、40 g 和50 g。为了探究温度对传感器灵敏性的影响,水标试验分别在40℃和20℃的水温下分别进行。最后通过计算土压力盒上的水压力,得到土压力盒输出电压与水压力的线性关系,即水标系数。

式中:K1为水标系数;σ1为水压力;V 为输出电压。

图2 土压力盒布设
2.4.2 不同砂层厚度下的砂标试验 为探究砂层厚度对标定系数的影响,通过离心模型试验的方法,改变土压力盒上的砂层厚度进行试验。首先在模型箱侧壁粘贴保鲜膜,将金属板平放于模型箱底部,金属板两侧使用金属块固定。然后根据2.3 节中砂雨法制样结果,对1#砂进行制样,制样相对密度控制在0.9,在土压力传感器上分别撒砂10 cm、20 cm、30 cm 和40 cm,并在模型箱顶部固定激光位移传感器,以测量模型加载过程中土样沉降,最后控制离心加速度按照10 g、20 g、30 g、40 g和50 g 进行逐级加载,每级加速度稳定10 min。最后通过拟合计算得到的土压力盒上的竖向土压力和土压力盒输出电压的线性关系,得到土压力盒的砂标系数。
2.4.3 不同砂颗粒粒径下的砂标试验 为探究在土压力传感器标定过程中,砂颗粒粒径对传感器标定结果的影响,根据2.3 节中砂雨法制样结果,分别对2#和3#砂进行制样,并将土样相对密度都控制为0.9,撒砂厚度控制在10 cm 左右,撒砂结束后仍然在模型箱顶部固定激光位移传感器测量土体沉降。然后通过离心模型试验,将离心加速度逐级稳定在10 g、20 g、30 g、40 g 和50 g 进行试验,每级加速度稳定时间同样为10 min,最后通过2.4.2 节中同样的方法得到2#砂和3#砂的砂标系数。模型布设如图3 所示。

图3 砂标试验模型布设
3 试验结果分析
3.1 砂雨法制样中落距-密实度关系图4 为不同采砂口落距与相对密实度关系曲线。通过对图4 的分析,可以得出:对于某一特定的出砂口,砂土相对密实度随落距的增大而增大,但增长速率逐渐减小。即在相对密实度较低的范围,落距的变化对相对密度影响较明显;在相对密实度较高的范围,落距变化对砂样密度的影响不明显。另外,不同的出砂口的落距-相对密实度关系也不相同。网眼式出砂口在落距相对较低时,密实度随落距的升高增加较快,随后逐渐趋于稳定;而鸭嘴式出砂口在撒砂过程中,随着落距的升高密度的变化相对比较缓慢。另外,对于不同的粒径的砂颗粒,制样得到的密实度变化范围也不同。本文中,1#砂、2#砂和3#砂都需要制得密实度为0.9 的土样,因此,分别使用洞眼直径为3 mm 和5 mm 的网眼式出砂口,控制落距分别为1 m 和0.6 m 制得1#砂和2#砂试样;使用宽度为5 mm 的鸭嘴式出砂口,控制落距为1 m,制得3#砂试样。
3.2 温度变化对传感器标定结果的影响在进行标定试验时,由于土压力盒标定试验中使用了12 只传感器,数据较多,本文仅挑选出两只传感器的结果作为空载时的说明,编号为1、2 和3 号的传感器数据水标结果作为说明。图5 为空载时两只土压力盒随加速度变化的曲线,由图5 结果可以看出,虽然土压力盒表面没有土体荷载,加速度从0 加载并稳定在50 g 时依然会导致土压力盒输出电压先增大后稳定在某一值附近。但输出电压变化量很小,对后续标定系数的计算几乎不产生影响。
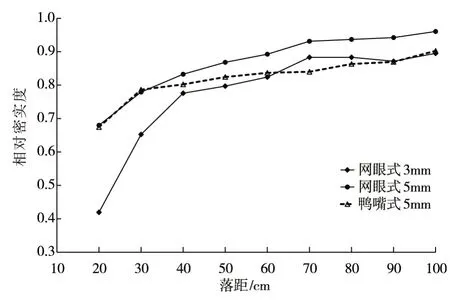
图4 不同出砂口落距与相对密实度关系
图6 为不同水温下3 只土压力传感器的水标试验结果。从图6 可以看出,当土压力盒在40 ℃和20 ℃的温度环境下分别进行工作时,随着加速度的逐渐增加,传感器的输出电压也在逐渐升高,卸载时传感器输出电压也在随着加速度的逐级降低而减小,且加载和卸载基本呈线性变化。在同一温度下,当离心机卸载至与加载相同加速度时,传感器前后的输出电压基本相同。另外,每只传感器在40 ℃和20 ℃的水中工作时,在同一离心加速度下每只传感器的输出电压也基本相同。由此可见,40 ℃和20 ℃的温度变化对传感器正常工作影响不大。
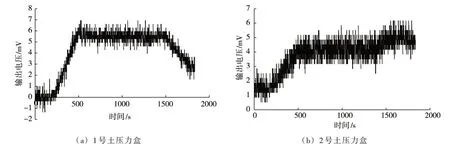
图5 空载时两只土压力盒输出电压随加速度的变化情况

图6 不同水温下3 只土压力盒水标试验结果
3.3 砂层厚度对传感器标定结果的影响首先,由激光位移传感器测量得到1#、2#和3#砂土样在加速度稳定至50 g,制样相对密实度为0.9 时,土样沉降分别为1.102、0.502 和0.799 mm,经计算发现,土体沉降对土样密实度和标定结果几乎没有影响。图7 为3 只土压力盒在不同砂层厚度下,分级加载时加速度与输出电压的关系,本文仅对加载时的土压力盒数据输出情况进行说明。由图7 可以看出,随着加速度的逐级增加,传感器的输出电压也在逐渐升高。通过对比同一传感器在不同工况下的输出电压值可以发现,土压力传感器在水标时输出电压曲线与传感器上撒砂10 cm 时的输出电压曲线比较接近,拟合直线线性度在0.99 以上,线性度较好;在撒砂厚度为20 cm 时传感器标定系数拟合直线线性度小于0.99。在砂层厚度为30 cm 时传感器输出电压曲线开始出现非线性趋势,而在砂层厚度为40 cm 时非线性趋势最为明显,线性度均小于0.98。
图8 是离心机加载稳定后3 只传感器输出电压和砂层厚度的关系,可以看出,随着砂层厚度的增加,3 只土压力传感器的标定系数在逐渐增大。这是因为镶嵌有土压力传感器的金属板平放于模型箱底部,当砂样厚度逐渐增大时,随着加速度的不断增加,砂颗粒与侧壁的摩擦作用越来越显著,这最终导致上层土压力无法全部传递到土压力传感器上,也就是发生了模型试验中的边界效应[13],从而导致土压力盒感应膜变形出现非线性变化,土压力传感器的输出电压也就相对减小。而利用公式σ=γz·ng 计算土压力时未考虑这种现象,致使计算土压力σ偏大,进行标定系数K 的计算时结果也会相应增大。而当砂层厚度较小时,土压力计算值相对比较准确,土压力传感器输出电压曲线的线性度也较好,通过拟合得到的标定系数也较为准确,与水标试验结果也最为接近。这也与Therous 等[14]的看法基本相同。另外,3#砂颗粒平均粒径为1.609 mm,Ovesen[15]指出颗粒粒径大小会影响界面土压力盒测量结果,为求准确,测量厚度应至少大于30 倍的颗粒粒径,因此3#砂砂层厚度至少应为5 cm。为了增加试验结果的可靠度和后续试验结果的比较,适当增大撒砂厚度。基于此结果,本文在后续试验选择砂层厚度10 cm(实际撒砂厚度8~10 cm)下土压力传感器的标定系数进行试验后的数据处理与计算。
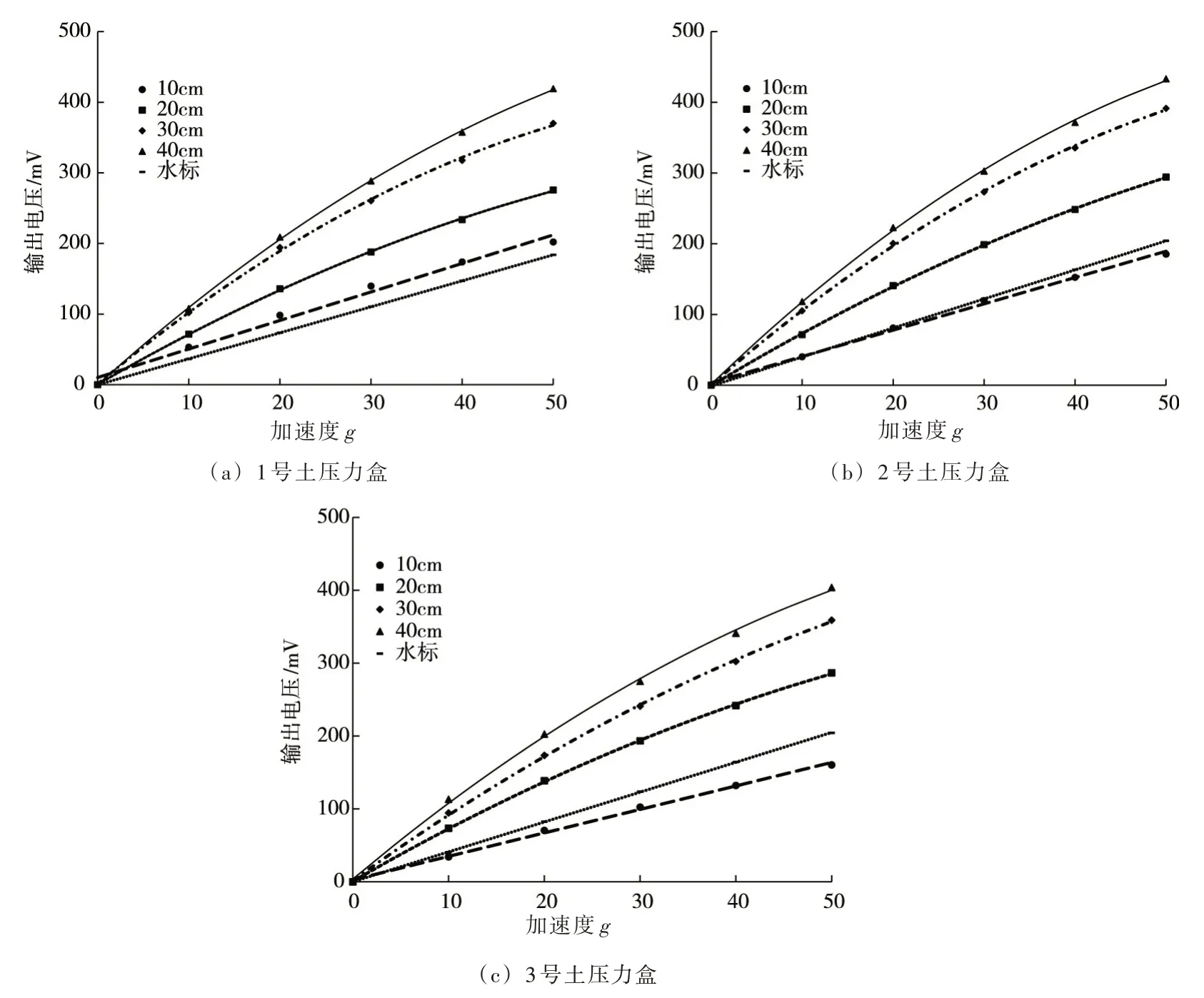
图7 3 只土压力盒砂标试验结果
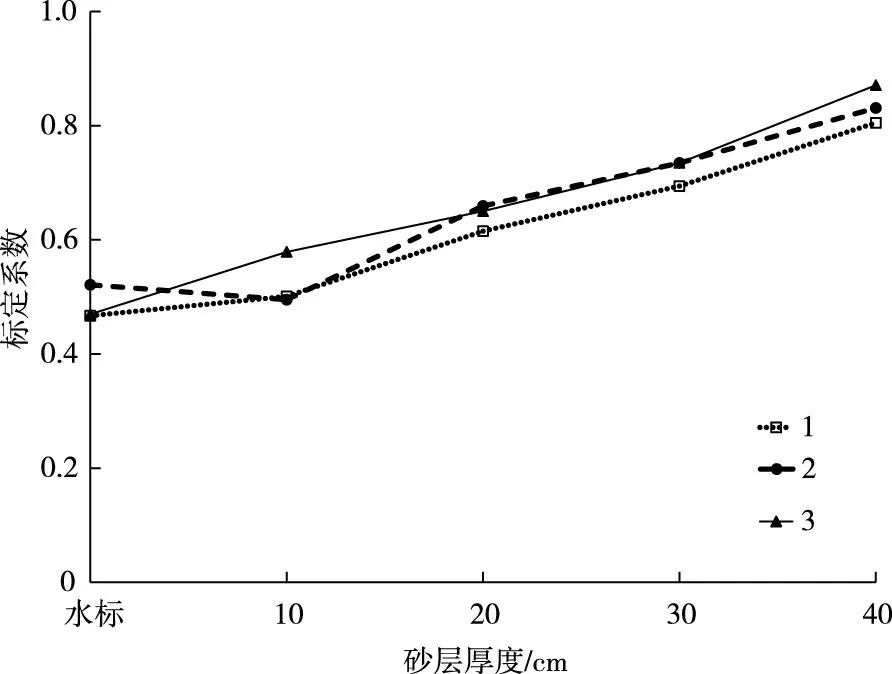
图8 3 只土压力盒标定系数与砂层厚度的关系
3.4 颗粒粒径对传感器标定的影响由图9 中对不同粒径砂土中土压力盒的标定结果可以看出,在相对密度0.9 下,1#砂中土压力盒的标定结果与水标结果相接近,随着土样颗粒粒径的增加,土压力传感器的标定系数也在逐渐增加。Miura 等[16]分别使用不同粒径的砂土对土压力盒进行标定时也出现了这种情况,他认为出现这种现象的原因是因为随着土样颗粒粒径的增大,材料的刚度降低,挠度增大,同时侧摩阻力也增大。他对不同砂土试样进行试验后发现,砂土颗粒的刚度随着粒径的增大而减小。Egan 和Merrifield[17]引入了一个衡量土压力盒性能品质的数值指标CAF,又称作土压力盒作用因数,其定义为:

式中:σce为测点处土压力盒表面的法向应力;σ0为无土压力盒时测点处土压力盒表面位置的法向应力。
Clayton 和Bica[18]对式(2)进行了改良,提出了一个能表征土压力盒感应膜和土体两者刚度共同影响的设计参数,即柔度因数F,定义如下:

式中Es为土体的杨氏模量。这样,土压力盒作用因数CAF 可用柔度因数F 表示为:

当土体的模量减少时,柔度因数F 也相应减少,这意味着土压力盒感应膜的刚度增大,土压力盒反应变得不灵敏,则在测量土压力时传感器输出信号变小导致输出电压减小。而土压力盒标定系数是传感器上土压力和输出电压的比值,在本文中,制样相对密度为0.9 时,1#、2#和3#砂的密度分别为1.576、1.614 和1.682 g/cm3,在同一土样深度处计算得到的竖向土压力也在变大,土压力盒输出电压的减小就导致了传感器标定系数随着颗粒粒径的变大而变大。

图9 砂颗粒粒径与传感器标定系数的关系
4 超重力场中不同土样K0值测量
为探究土压力传感器标定结果的准确性,同样在制样相对密度为0.9 的条件下,对1#砂、2#砂和3#砂的静止侧压力系数展开了测量。试验首先在模型箱侧壁粘贴保鲜膜,然后将金属板固定在模型箱两侧,使墙板无侧向变位,模型布设如图10 所示,试验装置如图11 所示。
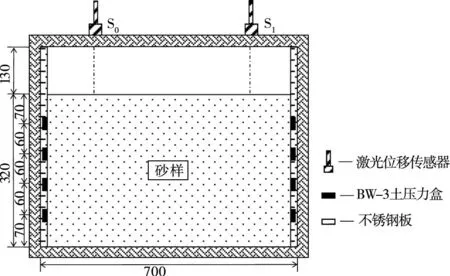
图10 试验模型布置 (单位:mm)

图11 不同土样的K0值测定试验
由3.3 节的试验结果,为减少模型箱侧壁摩擦对土样底部土压力测量的影响,在模型箱中撒砂32 cm 左右,得以覆盖4 个土压力传感器,并在模型箱顶部固定激光位移传感器,以测量模型加载过程中土样沉降。最后将模型吊入至离心机中,控制离心加速度逐级加载至50 g 并稳定30 min。试验中竖向土压力通过计算得到,水平土压力通过土压力盒测量得到,然后通过拟合墙身高度方向上水平土压力与竖向土压力的线性关系得到土样的静止侧压力系数。
由图12 土压力盒的测量结果可以看出,2#砂与3#砂的测量结果曲线比较接近,与1#砂相去较远。由表1 可以看出,2#砂与3#砂颗粒组成较为类似,都是0.5~2 mm 的颗粒组成了试样中的绝大部分,土体的性质较为接近。1#砂中,大小为0.075~0.25 mm 的颗粒占到了土样成分的94.5%,土样的组成与2#砂和3#砂相差较大,导致测量结果差别也较大。土压力盒测得的土压力变化规律也与实际情况相符,这也证实了在离心机中采用上覆土层10 cm 厚的土压力盒标定方式是合理的。
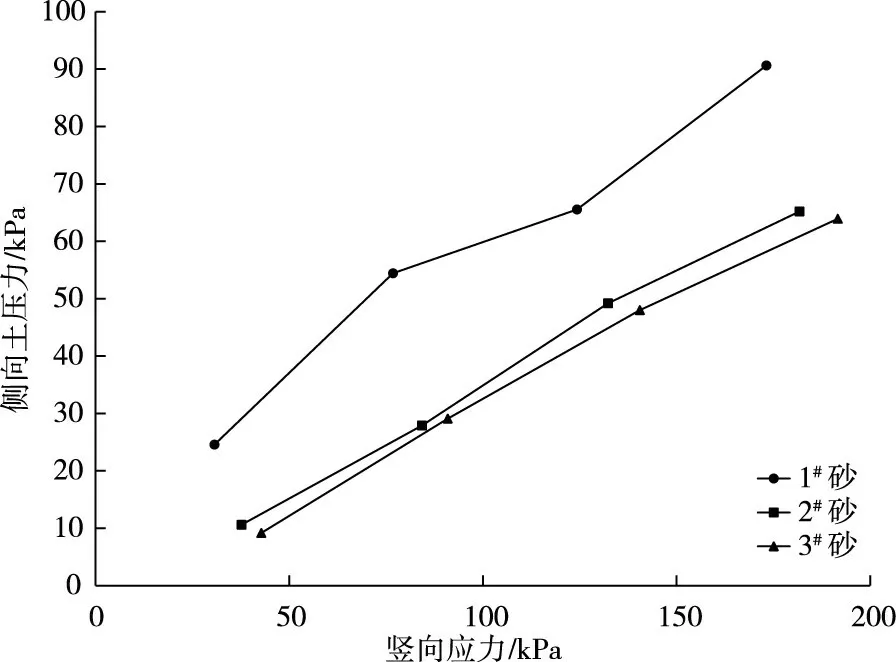
图12 墙身方向上不同土样土压力变化

图13 土样颗粒粒径与K0值变化关系
由图13 可以看出,随着土样颗粒粒径的增加,土样K0的试验值逐渐减小,这主要是因为土颗粒越小,土颗粒周围与之相接触的粒子数量就越多[14],这导致细颗粒土间的接触更为充分,在相同密实度下应力能得到更好的传递。通过三轴试验得到1#、2#和3#土样的有效内摩擦角分别为31.6°、35°和37.5°,利用Jaky 公式K0=1-sinφ'得到土样K0的计算值如图12 所示,可以看出计算结果与试验结果相比变化趋势类似,都是1#砂K0值最大,3#砂K0值最小,且Jaky 计算结果与试验结果相比数值偏大,这是因为Jaky 公式仅考虑了颗粒的有效内摩擦角对K0值的影响,而土颗粒间相互作用与众多因素有关[19-20],仅考虑有效内摩擦角与实际情况不符。
5 结语
本文通过离心模型试验,采取了多种方案对超重力场中土压力盒的标定方法进行了探究,并对其标定结果进行了验证,得到了以下几点结论:
(1)首先使用离心模型试验的方法,考虑温度对传感器测量的影响,在40 ℃和20 ℃的水温下对土压力盒进行了标定,结果表明40 ℃和20 ℃的温度变化对传感器测量结果的影响并不大。
(2)当对土压力盒进行砂标时,上覆土层厚度为10 cm 时传感器输出电压线性度最好,与水标结果最为接近,随着砂层厚度的增加,在砂层厚度30 cm 时传感器输出电压开始出现非线性趋势,在40 cm 时输出电压非线性趋势最为明显。
(3)在对同样密度不同粒径的土样中进行土压力盒标定时,标定系数随着土样颗粒粒径的增大而逐渐增大,这主要是因为土样颗粒粒径的增大会导致土样杨氏模量减小,土压力盒感应膜变形较小致使输出电压变小。
(4)通过使用BW-3 型土压力盒对制样相对密度为0.9 左右下的1#、2#和3#砂的静止侧压力系数进行了测定。结果发现,BW-3 型土压力盒的测量结果合理,土样K0值随着砂颗粒粒径的增大逐渐减小,并将结果与Jaky 公式的计算结果进行了对比,发现Jaky 公式的计算结果与试验结果整体趋势一致,但数值偏大。这是因为土颗粒间相互作用与众多因素有关,仅考虑有效内摩擦角对静止侧压力系数的影响是不合理的。
