0.6 H 层含沙量与垂线平均含沙量代表性探讨

张沈阳，唐东跃，吴 婷

（浙江省河海测绘院，浙江 杭州 310058）

1 问题的提出

垂线平均含沙量是泥沙动力学的一个重要内容，是研究输沙率的基础，也是研究河床变形问题的依据，在生产实践中具有重要意义。为研究、计算上的方便，常以垂线平均含沙量为表征，研究工程水域含沙量特性。传统的含沙量观测多采用测船定点观测方式，人工获取各层含沙量资料。该方式耗时耗力，且观测资料极其有限。随着浊度仪的普及，实现连续观测含沙量，解决以往含沙量资料零碎、偶然性大等问题。然而，浊度仪属于单点测量，无法实现垂向分层观测。若要获取垂向各层含沙量信息，则必须在垂线上布设一连串的浊度仪，该方法往往受水域环境限制，实际操作无法开展。因此，当特殊情况下无法获得垂线平均含沙量时，0.6H层含沙量是否可以表征垂线平均含沙量成为一个实际的工程问题。

本文旨在通过实测资料，找出单点含沙量（0.6H层）、两点平均含沙量（表层 — 底层平均）、三点平均（表层 —中层 — 底层平均）含沙量与垂线平均含沙量的相关性，通过各相关性的比较，分析及论证0.6H层含沙量的代表性。

2 资料获取

本文选取2018 年杭州湾大潮、中潮、小潮实测含沙量资料进行分析，该实测站点的水深大于4 m，根据规范[1]采用六点法（面层，0.2H层，0.4H层，0.6H层，0.8H层及底层，H为相对水深）观测。含沙量的测量方式为人工定点分层取样，于一个潮周期内每小时整点观测，观测前后半小时加密，观测时长约27 h，获取的水样通过实验室烘干及计算，最后得到垂向6 层的实测含沙量资料。根据该实测资料，计算垂线平均含沙量，公式为：

3 相关性分析

以大潮实测含沙量为例，将实测含沙量及基于实测资料计算的垂线平均含沙量作相关性分析，得实测含沙量与垂线平均含沙量的线性关系，结果见图1 ～ 3。根据各线性关系，计算垂线平均含沙量，并将其与实测含沙量计算的垂线平均含沙量比较，得到相应的误差值，结果见表1 ～ 3。

图1 单点（0.6 H 层）含沙量与垂线平均含沙量相关性图

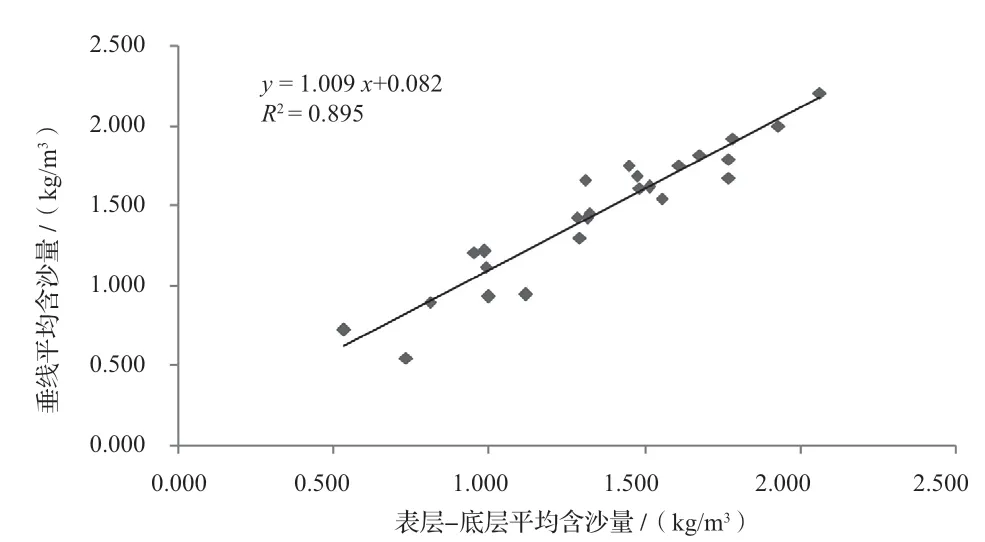
图2 两点（表层、底层）平均含沙量与垂线平均含沙量相关性图

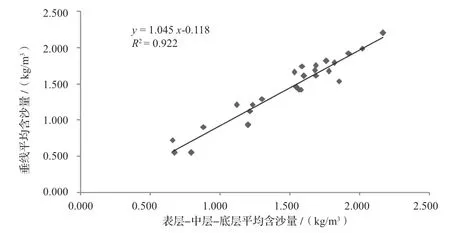
图3 三点（表层、中层、底层）平均含沙量与垂线平均含沙量相关性图

表1 单点（0.6 H 层）含沙量计算误差统计表

表2 两点（表层、底层）平均含沙量计算误差统计表

表3 三点（表层、中层、底层）平均含沙量计算误差统计表

由上述图表可得：实测含沙量与垂线平均含沙量具有较高的相关性，单点、两点平均、三点平均含沙量与垂线平均含沙量相关性均在85%以上，具有较高可信度。

将实测值计算的垂线平均含沙量及根据相关性公式计算的垂线平均含沙量进行误差分析，结果显示误差率均在15%以内，其中单点法为13%、两点法为15%、三点法为11%。由此可见，两点法由于缺少中间层含沙量，误差率略有提升。单点法误差率与三点法较为接近，表明0.6H层含沙量代表性较高。

4 实测含沙量与垂线平均含沙量比较

为了进一步论证0.6H层含沙量代表性，将大潮、中潮、小潮0.6H层含沙量、两点平均含沙量、三点平均含沙量均与垂线平均含沙量进行比较，结果见图4 ～ 6。

图4 大潮3 种方法计算的含沙量与垂线平均含沙量对比图

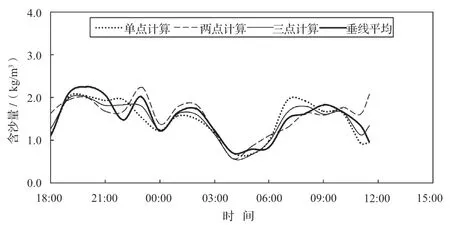
图5 中潮3 种方法计算的含沙量与垂线平均含沙量对比图

图6 小潮3 种方法计算的含沙量与垂线平均含沙量对比图

由图4 ～ 6 可知：3 种方法计算值和垂线平均含沙量均较为接近，其中单点法的代表性在小潮表现较为突出，明显优于其他2 种方法。

5 结 论

本文利用实测资料对3 种方法计算的含沙量及垂线平均含沙量进行比较分析，论证0.6H层含沙量代表性问题。结果表明：

（1）单点法（0.6H层）含沙量与垂线平均含沙量相关性较高，在85%以上，表明0.6H层含沙量具有较高代表性。

（2）两点法（表层、底层平均）含沙量由于缺少中间层权重，存在一定缺陷，相关性略低于单点法及三点法。

（3）多数情况下，三点法精度最高。但小潮汛受潮动力影响较小，单点法精度略优。

本文的论证基于实测资料，故实测资料的准确性需引起重视。另外，由于两点平均、三点平均含沙量计算未考虑流速加权，存在一定缺陷。若条件允许，建议同步观测流速，进行流速加权，精度会有质的提高。