基于工程混合物理论的饱和裂隙岩体组合本构模型

胡亚元，王 超

（浙江大学 滨海和城市岩土工程研究中心，浙江 杭州 310058）

1 研究背景

在经典岩体力学中，受试验能力限制，通常把岩体拆分成完整岩块和节理结构面分别进行试验和本构研究，然后再通过整合完整岩块和节理结构面的本构方程来建立岩体的等效连续介质本构模型，即岩体组合模型。Morland［1］、Noorishad 等［2］和Wang 等［3］建立了干燥岩体的组合本构模型，王媛等［4-5］和盛金昌等［6］采用Terzaghi 有效应力原理建立了饱和岩体的组合本构模型。林鹏等［7］根据饱和岩体的Terzaghi 原理法组合模型，采用三维非线性有限元法数值模拟了溪洛渡拱坝基岩的变形和稳定。张国新［8］对小湾、溪洛渡和锦屏等水电站蓄水后大坝及边坡变形进行仿真分析后发现，饱和岩体Terzaghi 原理法组合本构模型夸大了浮托力作用，会导致数值计算变形和应力结果失真。为了克服饱和岩体Terzaghi 原理法组合模型的缺陷，一些岩体力学学者建议采用Biot 理论来建立饱和岩体本构模型［9］。

尽管饱和介质Biot 线弹性理论已发展得比较成熟完善，但裂隙岩体具有比较明显的非线性和塑性特性，把Biot 理论推广到裂隙岩体领域依然存在瓶颈。难点在于Biot 理论建议采用单一的Skempton有效应力来建立饱和岩体本构模型，Skempton 有效应力中的Biot 系数在非线性和塑性本构关系中不再是一个定值，如何合理确定Biot 系数成为制约饱和裂隙岩体本构理论发展的一个关键因素。与Biot理论相比，混合物理论从普适性的力学守恒定理出发，消除了传统方法中许多人为的任意假设，具有严密的数理依据［9-11］。但当前混合物理论普遍采用固相应变和流体渗出量作为应变量来研究饱和岩体的本构性质［12］，难以与岩体力学中的完整岩块和节理裂隙结构面的力学试验和本构模型相结合。据笔者所知，目前还未见有关采用混合物理论创建饱和岩体组合模型的研究文献报道。

本文首先从工程混合物出发，在小应变条件下，采用固相基质应变和骨架应变作为应变量来建立饱和多孔介质的内能平衡方程，根据功共轭量之间的力学关系来揭示饱和多孔介质的一般本构规律。其次，按照经典岩体力学理论把岩体分为完整岩块和裂隙结构面［13］，把饱和裂隙岩体近似地视为孔隙由裂隙组成的饱和多孔介质。最后根据饱和多孔介质的一般本构规律整合出完整岩块和裂隙结构面本构关系，建立饱和裂隙岩体的组合本构模型，供饱和岩体工程理论和数值分析之用。由于工程混合物理论以固相基质应变和骨架应变为应变量建立饱和多孔介质本构模型，固相基质应变等同于完整固体变形引起的固相应变，骨架应变等同于孔隙变形引起的固相应变，因此建立在工程混合物理论之上的饱和岩体组合模型理论，能合理地与经典岩体力学中完整岩石和节理结构面的力学试验和本构特性相结合，不但克服了经典混合物理论难以表征完整岩块和节理结构面力学性质的困境，而且避免了饱和裂隙岩体力学中Terzaghi 原理法组合模型夸大流体浮托力作用的缺陷和Biot 理论难以确定Biot 系数的困难。

2 小应变条件下的饱和多孔介质一般本构理论

工程混合物理论认为，固流两相在饱和多孔介质中存在两种不同尺度的构形［9-11］：（1）组分实际存在的细观真实构形，如饱和岩体中的完整岩块和裂隙中流体。它们产生的应变称为组分基质应变，固相基质应变用列向量εRS表示，εRS=［εRSxx，εRSyy，εRSzz，εRSxy，εRSyz，εRSzx］T，固相基质体应变用εRSV表示，流相基质体应变用εRFV表示；（2）组分按体积分数平均化到混合物后连续变化的宏观构形，它所产生的应变称为组分应变，固相应变用列向量εS表示，εS=［εSxx，εSyy，εSzz，εSxy，εSyz，εSzx］T，固相体应变用εSV表示，流相体应变用εFV表示。设下标S 表示固相，下标F 表示流相， α ∈{ S ,F }为组分特征变量。 ρRα为α 组分的基质密度（又称为真实密度）， ρα=φαρRα为组分密度（又称为平均密度），φα为体积分数。对于饱和多孔两相介质，体积分数φα满足φS+φF=1。

设Ia=[1,1,1,0,0,0]T，上标T 表示矩阵的转置运算。 σ 为饱和多孔介质所受的总应力列向量，为固相组分承受的应力列向量，为固相组分球应力； σRS=σS/φS0为固相基质应力列向量，为固相基质球应力； σFm为流相组分承受的球应力，u=σFm/φF0为流相基质球应力或称为孔压。根据工程混合物理论有［10，14］：

固流两相基质体应变εRSV和εRFV在小应变条件下的定义为［10，14］：

小应变条件下固相骨架应变εSf定义为固相应变与固相基质应变之差［10］：

固相体应变记为εSV，固相骨架体应变（又称体积分数应变［14］）记为εHV，根据工程混合物理论有：

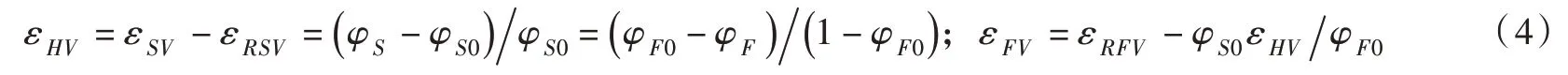
式（4）的前一式表明，固相骨架体应变取决于孔隙率变化。令σ′=σ-uIa为Terzaghi 有效应力；为流固两相流速差异引起的动量供应量，在饱和岩土中表现为流体渗透引起的拖曳力。根据工程混合物理论，忽略热传递和热源，饱和多孔介质的内能平衡方程可表示为［10，14］：

式（5）表明，饱和多孔介质的内能等于固相骨架变形功、固相基质变形功、流相基质体应变变形功和渗流引起的耗散功之和。

假定各相温度θ 相等且恒定以及均匀化响应原理［10，14］成立，则固相骨架变形产生的内能UH、固相基质变形产生的内能URS和流相基质变形产生的内能URF相互独立。饱和多孔介质的内能可表示为：

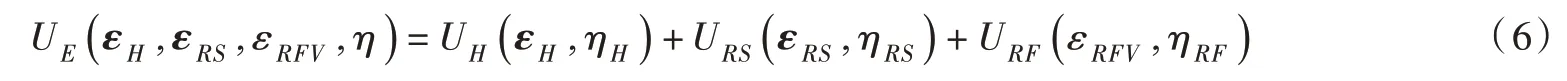
式中：η 、ηH、ηRS和ηRF分别为饱和多孔介质总熵、固相骨架、固相基质和流相基质所含有的熵。由熵的可加性有η=ηH+ηRS+ηRF，根据式（6）有：

根据热力学状态变量相互独立变化、温度的定义及各相中温度相等的性质得：

式中θ 是一个常数，可省略不写。根据式（10）可建立饱和裂隙岩体的组合本构模型。

3 饱和裂隙岩体的组合模型

完整岩块虽然含有微小缺陷和孔隙，但它们的渗透性小，可忽略岩块与微小缺陷和孔隙中流相之间的相互耦合作用。同时，岩体力学试验通常对包含微小缺陷和孔隙的完整岩块进行试验，获得的完整岩块力学特性包含了微小缺陷和孔隙的变形性质。故可把含有微小缺陷和孔隙的完整岩块视为一个整体，饱和裂隙岩体可视为由完整岩块构成固相基质和由裂隙构成孔隙的饱和多孔介质［1-7，13］，饱和裂隙岩体的固相基质应变εRS等同于完整岩块变形引起的固相应变，骨架应变εH等同于裂隙变形引起的固相应变，故我们可以通过完整岩块和裂隙分别随荷载的变形特性来分析固相基质和骨架的力学特性。在经典岩体力学中［13］，完整岩块与裂隙分开进行试验和本构模型研究［13］，这意味着它们的力学性质是相互独立的，故饱和裂隙岩体满足工程混合物理论的均匀化响应原理，式（10）对饱和裂隙岩体成立。式（10）表明：Terzaghi 有效应力σ′决定裂隙孔隙率变化引起的固相骨架应变εH，固相基质应力σRS决定完整岩块应变εRS，裂隙孔压u 决定裂隙流相基质体应变εRFV。由式（3）可知裂隙岩体应变εS等于固相骨架应变εH和固相基质应变εRS之和。

3.1 完整岩块本构方程完整岩块的统计损伤本构模型可表示为［15］：

式中：qRS=σRS1-σRS3为完整岩块的偏应力；σRS1为完整岩块的第一主应力；σRS3为完整岩块的第三主应力；εRS1为完整岩块轴向应变；ERS0为完整岩块的初始弹性模量。εRSa与m 为Weibull 分布参数［15］，当εRSa=∞表示不考虑完整岩块损伤因子的影响。根据式（11）得切线杨氏模量ERS为：

设υRS0为初始泊松比； υRS0为峰值泊松比； ω 为泊松比增长指数，岩体的泊松比υRS公式取为［16］：

当完整岩块卸载与重复加载时，回弹模量和泊松比取εRS1=0 时的ERS和υRS值，以简单反映完整岩块受力变形的不可逆性［3］。令柔度矩阵：

可得完整岩块的本构关系为：

3.2 裂隙本构方程

3.2.1 不含流体的单一节理本构模型 单一节理本构模型包括法向闭合、切向剪切和剪胀三类本构方程。

（1）法向闭合方程。Bandis 等［17］通过大量试验数据，发现法向压应力σn与节理法向位移δn之间存在双曲线本构关系：

式中A、B 为模型参数。

设裂隙孔隙率变化引起的节理法向位移为δHnn，孔隙率保持不变时岩体基质变形引起的节理法向位移为δRSn，两者之和为总法向位移δn。设裂隙开度为b，注意到孔隙率保持不变时裂隙部分的应变等于完整岩块的应变，故δHnn的计算公式由式（15）—（16）可得：

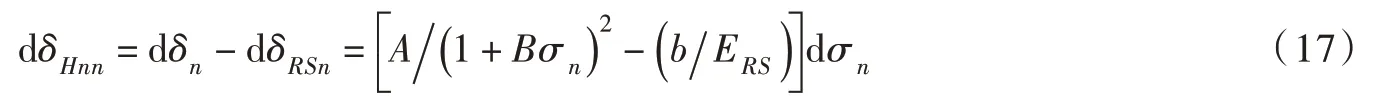
（2）切向剪切方程。节理剪切应力τ与剪切位移δHs的关系可表示为［18］：

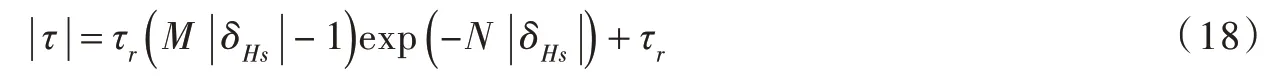
式中：τ与δHs同号；M、N 为模型参数，根据下面的式（19）和式（20）确定：

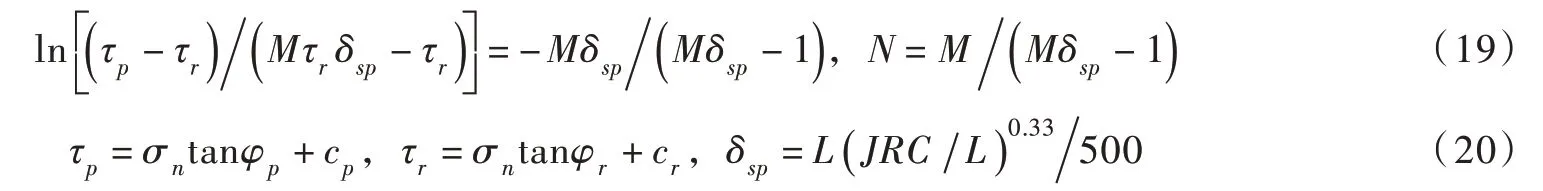
式中：τp为峰值剪切强度； τr为残余强度；δsp为峰值强度对应的剪切位移； φp为节理峰值摩擦角；cp为节理峰值黏聚力； φr为节理残余摩擦角；cr为节理残余黏聚力；JRC 为节理粗糙系数［18］。

（3）剪胀本构。 设δHv为节理剪切位移δHs引起的那部分法向位移，JCS 为节理岩壁抗压强度，k 为系数，对于粗糙节理面k=4，σ0为初始剪胀角， δvr为最大剪胀量， δso为剪胀量为零时所对应的剪切位移，借鉴肖卫国等［19］提出的研究成果，考虑JCS 和法向应力σn影响的非线性剪胀本构方程取为：

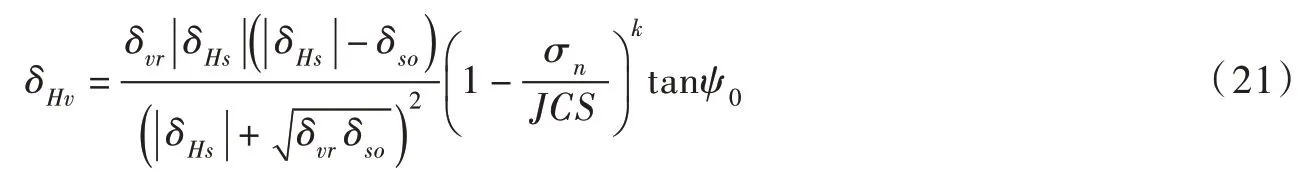
3.2.2 流体饱和裂隙的单一节理本构模型 由3 节首段文字可知，在饱和裂隙岩体中，裂隙孔隙率变化引起的固相应变等于骨架应变，它由Terzaghi 有效应力唯一决定。故对于流体饱和裂隙，式（17）、式（20）和式（21）中的σn均要用Terzaghi 有效应力σ′n=σn-u 所代替，根据式（17）、式（18）、式（21）和δHn=δHnn+δHv可以求得用总法向位移增量dδHn与节理剪切位移增量dδHs表示的节理法向应力增量dσ′n与节理剪切应力增量dτ为：

式中节理刚度元素Knn、Kns、Ksn和Kss满足：

当节理法向应力卸载与重复加载时，法向应变和应力的关系与式（16）相同，但其模量参数按卸载点处首次加载模量的两倍取值［19］。当节理剪切应力卸载与重复加载时，出于简化，剪应力应变关系按线性变化，加卸载时的剪切模量取为剪切应变等于零时的模量，以简单反映节理剪切变形的不可逆性。

3.2.3 多组节理的骨架本构模型 岩体节理一般分布多组节理。对于多节理面，每组节理面都独立设置局部坐标系。图1 所示为岩体单元体内第α组节理分布图。上标α代表第α组节理， Sα为第α组节理间距，节理局部直角坐标轴为（na，sa，ta）， na为节理面单位内法向向量，sa为节理面单位走向向量，单位向量ta根据右手准则确定。

图1 节理组示意图［3］

3.3 饱和裂隙岩体的组合本构方程把式（15）和式（26）代入式（3）后利用式（1）和σ′=σ-uIa，可得饱和岩体的固相应变为：

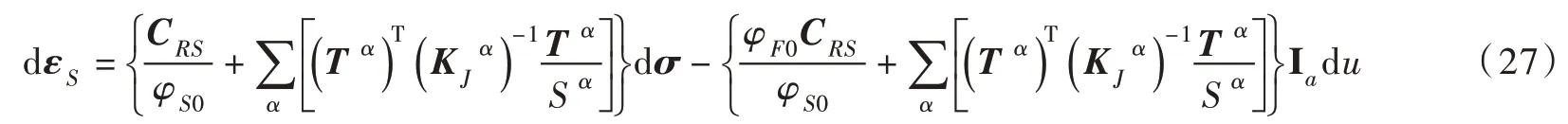
在饱和裂隙岩体工程中需要计算流体渗出岩体的渗流量，定义渗流量为ξF=φF0(εFV-εSV)。假定裂隙流相基质符合线弹性模型，有εRFV=CFu ，式中CF为流相柔度系数。根据式（4）、式（15）、式和εRFV=CFu 可得：

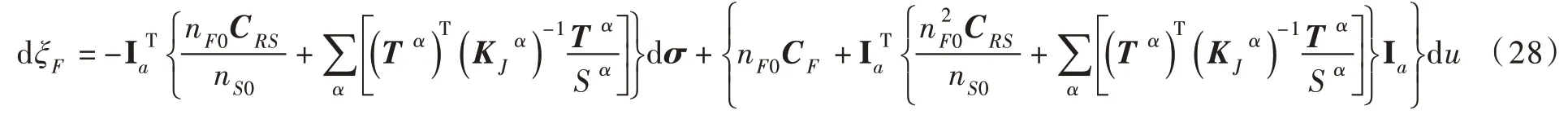
式（27）—式（28）就是饱和裂隙岩体的组合本构模型。

4 算例

为了更加直观地理解本文提出的饱和裂隙岩体组合模型的特点和工程用途，本节分析了3 个算例。算例1 对比了与以往饱和裂隙岩体组合模型的异同，分析了这些异同背后的力学机制；算例2 通过试验来验证本文饱和裂隙岩体组合模型的正确性；算例3 通过有限元分析成果证明本文饱和裂隙岩土组合模型的实用性，阐明裂隙结构面各向异性对饱和裂隙围岩变形特性的影响规律。

4.1 算例1采用与文献［4］同样的岩块和节理力学参数来进行对比分析。完整岩块弹模ERS= 20 GPa，泊松比νRS= 0.2，不考虑完整岩块损伤效应，即εRSa=∞，裂隙孔隙率为0.8%，节理Knn= 7.5 GPa/m；Kss= 5.0 GPa/ m，Ksn= Kns=0，间距S1=4 m，节理法向与Z 轴一致。饱和裂隙岩体的Terzaghi 原理法组合本构模型的计算公式为［4-5］：

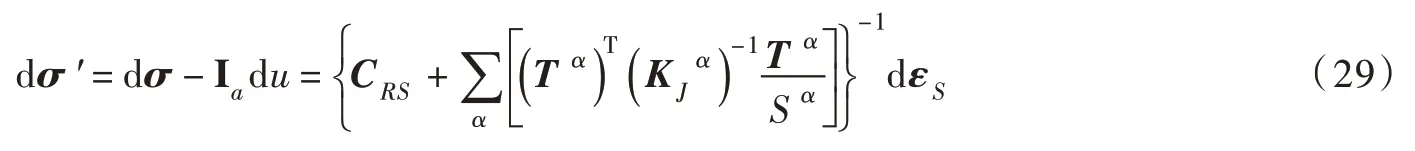
本文建立的饱和裂隙岩体组合本构模型的计算公式根据式（27）可得：

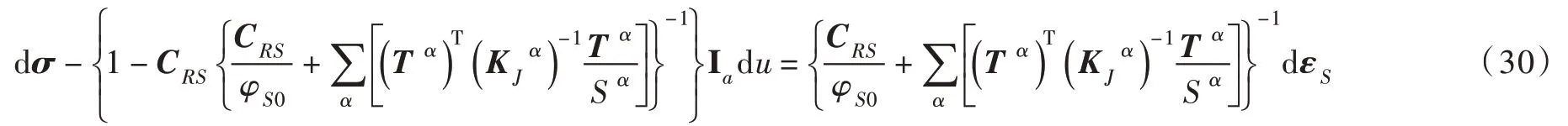
把完整岩块和裂隙力学参数代入式（14）和式（25）第一式可得CRS和K1

J 。根据节理法向与Z 轴一致可知n1=［0，0，-1］、s1=［0，1，0］和t1=［1，0，0］，代入式（25）第二式可得T1。把CRS、T1、S1=4 m 和φS0=99.2% 代入到式（29）和式（30），获得饱和裂隙岩体的Terzaghi 原理法组合本构模型为：

本文根据工程混合物理论建立的饱和裂隙岩体的组合本构模型为：

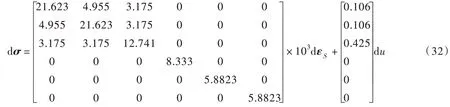
式（29）表明，在饱和裂隙岩体的Terzaghi 原理法组合模型中，Terzaghi 有效应力不但决定裂隙孔隙率所对应的骨架应变，而且决定完整岩块所对应的固相基质应变，故文献［4］获得的组合模型的Biot 系数等于1.0。而在式（30）中，Terzaghi 有效应力只决定骨架应变，固相基质应变由固相基质应力决定，故本文获得的组合模型的Biot 系数小于1.0。表现在式（31）和式（32）中，与岩体位移相关的刚度矩阵两者相差不大，但与孔压相关的孔压系数两者相差较大，后者为一个小于1.0 的Biot 系数。事实上，饱和裂隙岩体中的完整岩块类似于饱和土中的土颗粒。当土颗粒压缩变形不可忽略时，决定固相应变的有效应力需要对孔压进行折减才比较符合岩土实际受力特性［8，20］。然而在Terzaghi 原理法组合模型中，Biot 系数等于1.0，从而夸大了孔压的浮托力作用。在式（32）中，由于裂隙间距有4 m，分割岩块的裂缝间距比较远，故组合模型的孔压系数不但比1.0 要小得多，而且由于裂隙分布的空间差异呈现出各向异性特性。本文根据工程混合物理论建立饱和裂隙岩体组合本构模型时未利用Biot系数，避免了采用Biot 理论建模时需要事先确定Biot 系数的困难。

4.2 算例2Haji-Sotoudeh 等［21］对大理石裂隙部位的流固耦合特性进行了等向压缩和水压试验研究。由于裂隙岩面凹凸不平，因此在裂隙开度范围内存在大理石矿物质，依然是一个饱和多孔介质，可以采用本文提出的饱和裂隙组合模型来进行理论预测。Haji-Sotoudeh进行等向压缩和水压试验数据见图2和图3中的散点所示。模型参数取值方法与文献［13］和［17］相同，裂隙破损处岩块弹模ERS=340 MPa，Bandis模型参数为A=0.056MPa-1·mm，B=0.45MPa-1。大理石裂隙开度为b=0.16 mm，节理法向与Z 轴一致。由于是等向压缩和水压试验，故无需确定节理剪切和剪胀模型参数和岩块损伤模型参数，把上述参数代入式（16）和式（29）—式（30），可得岩体应变随外荷载和孔压变化曲线，如图2—图3 中实线所示。从图2可以看出，Bandis节理法向变形模型比较合理地模拟外荷载随裂隙部位岩体应变的变化规律，从图3 可以看出，采用Terzaghi有效应力模型预测岩体应变时，相同孔压引起的岩体膨胀应变与试验值相比明显偏大，故采用Terzaghi 有效应力模型模拟饱和岩体变形时会低估岩体的沉降变形［8］；图3 中本文提出的组合本构模型比较合理地模拟孔压随裂隙岩体应变的变化规律，因此它比Terzaghi有效应力组合本构模型能更合理地模拟流固耦合特性。本文建立饱和岩体组合本构模型时，未采用Biot 理论中的Biot 系数及其Skempton 有效应力，更便于建立非线性和塑性饱和岩体本构模型。

4.3 算例3图4 所示为海底隧道的横截面图。海水深40.0 m，在离海底17.0 m 深岩层处建设一座直径为15 m 的海底隧道。隧道围岩中发育有两组裂隙，节理产状和力学参数见表1，完整岩块力学参数见表2，参数取值见文献［22］，由于完整岩块在剪切作用下具有明显的剪胀效应，当采用非线性弹性模型来模拟完整岩块受力特性时，峰值泊松比往往取大于0.5 的数值［16］，以便反映完整岩块的剪胀效应。岩体容重为25 kN/m3， φF0=0.16%，CF=0.5（GPa）-1，L=1 m，JRC=13，JCS=40 MPa，渗透系数根据立方体公式得Kxx0=1.963×10-4m/s，Kxz0=2.36×10-5m/s 和Kzz0=1.161×10-4m/s。

图2 外荷载随裂隙部位岩体应变变化

图3 孔压随裂隙部位岩体应变变化

图4 海底隧道地质图

表1 节理组产状和力学参数［22］

表2 完整岩块基本力学参数［22］

隧道横截面变形按二维平面应变问题分析，此时式（14）和式（25）简化为：

利用表1 所示的节理产状和力学参数和表2 所示的完整岩块力学参数，利用式（24）、式（27）、式（28）和式（33）建立饱和裂隙岩体组合本构方程，然后通过非线性有限元理论进行Fortran 程序编程数值计算，获得开挖稳定后隧道截面的水平和垂直位移如图5—6 所示。图5—6 表明节理形成的各向异性导致隧洞附近地层发生显著的不对称变形，隧道左上侧和右下侧地层向洞口内部水平挤入约10 mm，而隧道左上侧地层下沉约24 mm，右下侧地层隆起约16 mm。地层变形平面分布左上侧变形最大，右下侧次之，斜两侧最小，变形近似与隧道中轴线斜交对称。造成上述变形分布的原因是完整岩块被两组节理切割后成为各向异性岩体，如隧道中线附近第210 单元的饱和裂隙岩体组合本构方程为：

从式（34）可以看出，饱和裂隙岩体被节理切割后，本构方程刚度矩阵破坏了原有的对称性，具有明显的不对称特征，正应力和剪切力具有明显的交叉影响。受正应力和剪切力交叉作用影响，孔压与岩体剪切应力之间也存在相互耦合作用。这表明饱和裂隙岩体被结构面切割后具有非常强烈的各向异性力学特性，导致隧道围岩在开挖引起的水平对称荷载作用下产生与中轴线不对称的位移分布。

图5 开挖导致的地层水平方向变形 （单位：m）

图6 开挖导致的地层竖直方向变形 （单位：m）

5 结论

（1）根据工程混合物理论，把饱和裂隙岩体视为由完整岩块组成固相基质和由裂隙组成孔隙的饱和多孔介质，获得“固相基质应力决定完整岩块应变（固相基质应变），Terzaghi 有效应力决定节理裂隙变形（固相骨架应变），裂隙孔压决定流相基质体应变”的本构规律。研究表明，以固相基质应变和骨架应变为应变量的饱和多孔介质本构理论，与经典混合物本构理论相比，更容易表征和模拟完整岩块和节理结构面的力学试验和复杂力学性质，建立饱和裂隙岩体的组合本构模型。

（2）把本文提出的饱和裂隙岩体组合本构模型与Terzaghi 有效应力原理法建立的组合本构模型进行对比，分析结果表明，两者固相刚度矩阵相差不大，但孔压系数前者比后者要小得多。文中算例2表明，前者比后者更符合岩体力学试验。造成这种差别的原因是后者根据Terzaghi 有效应力原理来建立饱和裂隙岩体的组合模型，Biot 系数等于1.0，夸大了孔压的浮托力作用；而本文严格按照工程混合物理论的内能平衡方程来建立饱和裂隙岩体组合模型，能合理反映裂隙中流体的浮托力作用以及孔压对饱和裂隙岩体固相本构模型各向异性的影响。

（3）根据本文建立的饱和裂隙岩体组合本构模型，分析了海底隧道开挖过程中裂隙围岩的流固耦合工程特性。结果表明，由于围岩育有两组平行节理，使饱和裂隙岩体呈现出各向异性受力变形特性，导致围岩在隧道水平对称荷载作用下产生与中轴线不对称的位移分布。