基于压缩感知的矿井无线传感器网络目标定位
2020-07-27贺方圆宫晓玮祝玉超靳昊玥王文清
贺方圆,宫晓玮,祝玉超,靳昊玥,王文清
1. 中国矿业大学(北京) 机电与信息工程学院,北京 100083;2. 北京工业职业技术学院,北京 100042
无线传感器网络(Wireless Sensor Networks,WSN)定位技术[1]是由布置在定位区域内的大量参考节点通过无线通信方式自然组成的一个多跳自组织网络技术,用于感知、采集和处理覆盖区域内被感知对象的信息。WSN节点具有体积小、成本低、电池供电低功耗、可随意布置的优点,且每个节点都具有感知和通信功能。因此,WSN技术常用于公共网络信号无法覆盖或不使用公共网络而需建立独立定位通信网络的场合。煤矿井下没有GPS等公网信号,生产作业环境相对狭小复杂,人员活动区域受到限制,WSN更适用于煤矿井下目标定位。
在WSN矿井目标定位系统中,基于节点布置的定位方法是WSN定位的技术支撑,此类方法大多通过改进定位算法提高定位精度。如文献[2]提出了一种基于卡尔曼滤波的矿井移动节点定位算法,该方法利用卡尔曼滤波器对RSSI信号强度进行滤波和测距预估,并对移动节点进行校正,提高定位精度;文献[3]基于已布置的节点,提出无线传感器网络三阶段定位方法,该方法通过融合三个阶段的定位信息,实现矿井目标的精确定位。上述方法没有考虑节点数量和功耗,无法从根源上解决节点功耗大、目标定位精度低的问题。
在WSN非矿井目标定位方法中,一种基于压缩感知(Compressed Sensing,CS)算法[4-6]的WSN定位方法得到了广泛关注,此类方法利用CS算法通过信号少量稀疏采样可高概率重构这一特性,降低目标定位的工作量,提高定位精度。如文献[7]基于CS算法及目标的稀疏性和能量衰减特性,将目标定位问题建模为基于CS的稀疏信号恢复问题,设计了一种满足RIP性质的观测矩阵实现单目标和多类别目标的精确定位;文献[8]基于CS的传感器目标定位方法将目标所在区域划分为多个网格,根据锚节点以及通信半径建立观测矩阵,采用CS算法得到目标的粗略定位,再根据信号指标强度实现目标的精确定位。上述方法没有考虑WSN中数据收集的可靠性、通信半径的测量误差以及网格的划分密度,定位精度受到影响。
笔者基于CS算法提出一种新的矿井WSN目标定位方法。该方法提出两阶段定位方案:离线阶段和在线监测阶段。离线阶段通过建立信号强度稀疏矩阵构建离线指纹库;在线监测阶段通过测量少量参考节点的位置信息和实时监测目标节点信号强度值构建观测矩阵和测量值向量,并结合离线阶段建立的稀疏矩阵重构目标节点位置信号。该方法在目标定位时,仅需布置少量参考节点,并采集节点小部分信息进行数据处理,通过重构方法精确恢复目标位置信号,降低大规模布置参考节点和采集多余信息的工作量,降低节点功耗,同时防止过多参考节点间通信交叉干扰,减少信息采集误差,提高定位精度和定位效率。
1 矿井目标定位系统模型
基于WSN的矿井目标定位系统将参考节点获得的信号信息转化为节点与目标间的距离信息,根据相应定位算法确定目标位置。传统的定位算法常采用测距的三边测量解算定位算法(简称三边法)[9]和指纹定位算法(简称指纹法)[10-11]。
三边法是已知3个参考节点坐标,利用电磁波传输获得各参考节点与目标节点间的测量距离,并通过解算测量距离联立的方程组求得目标节点的位置。该方法对信号时钟同步、信号衰减模型、信号传播环境等要求较高,目标定位误差较大,因此近年来指纹法成为矿井目标定位的研究热点。
指纹法包括离线测量阶段和在线定位阶段。离线测量阶段对信号的传输距离与接收强度特征值进行测量,将信号强度测量值和对应测量点的位置标识信息作为指纹信息存储形成离线指纹库,指纹库中信号强度与位置信息一一对应。指纹库建立时,理论上矿井目标的位置坐标是连续的,但从工程上,任意坐标点的信号强度是不能连续测量和存储的。因此,提出将定位区域网格化并进行排序标号,再将目标节点分别布置在每个网格并发射信号,测量并记录布置在其他各个网格的参考节点接收到的信号强度值存储在矩阵中,即指纹库中存储的是所有网格位置和网格信号强度值的矩阵。在线定位阶段,通过实时测量信号强度值比对指纹库指纹信息,确定目标位置。但在线定位阶段不可能在每个网格处都放置参考节点,只能布设少量参考节点,而参考节点接收的目标信号强度值通过比对指纹信息可能会确定多个位置坐标。因此,指纹法定位会导致较大的定位误差。
CS原理[12]是选择少量包含足够大信息量的采样值,通过求解一个最优化问题大概率地重构原始信号,将少量参考节点得到的信号强度值看作CS算法的信号稀疏采样,在离线指纹库的基础上,通过CS重构算法得到目标节点的位置,即将目标定位问题转化为信号的恢复问题。由此本文提出基于CS算法的WSN矿井目标定位方法,即通过两阶段定位重构目标信号位置。第一阶段是离线指纹库建立阶段,对煤矿井下定位区域进行N个网格划分,N个参考节点和待定位目标按序分配在定位区域内,测量每个网格参考节点接收的N个目标信号强度值,得到信号强度值矩阵,连同各个网格的位置坐标一起存入指纹库,构建完备的离线指纹库;第二阶段是在线监测定位阶段,根据矿井巷道结构和无线传感器网络节点的通信距离等情况,构建少量参考节点的无线传感器网络,参考节点通过在线监测目标节点信号强度值构建测量值向量,再根据各个参考节点的位置信息构建观测矩阵,导入离线指纹库建立阶段构建的冗余字典,在观测矩阵和字典满足不相关的条件下,可以由少量的信号强度测量值向量通过CS重构算法恢复目标节点位置。定位系统模型如图1所示。
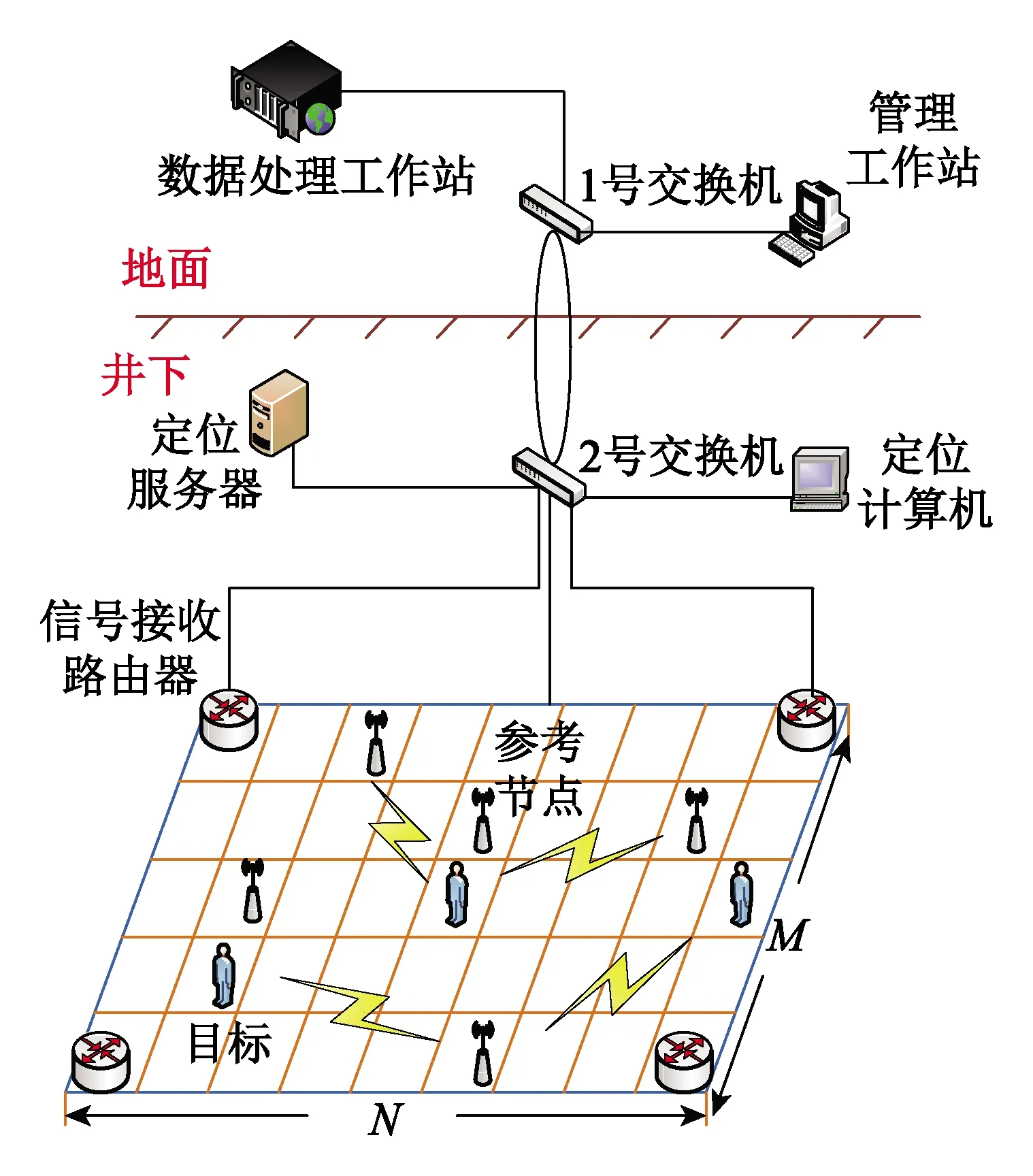
图1 矿井巷道定位系统示意图Fig.1 Schematic diagram of mine roadway positioning system
为对煤矿井下目标节点位置数据进行采集和处理,将整个矿井巷道定位区域拆分成若干个局部定位区域,在每个定位区域中心处放置一个网关,负责采集和管理本区域内目标节点和参考节点的信息,目标节点、参考节点和网关之间组成一个以网关为汇聚中心的无线传感器网络,如图2所示。由图2可知,每个参考节点都可以接收到各个目标节点周期性发出的信号,网关将参考节点监测到的目标节点信号强度等信息发送给定位计算机,定位计算机根据CS算法确定目标节点的位置。
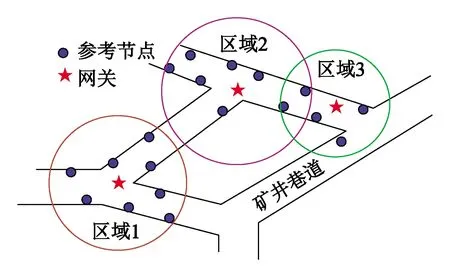
图2 矿井巷道局部定位区域布置示意图Fig.2 Schematic diagram of location area in mine roadway
2 CS算法数学模型
CS算法的目的是从少量采样信号y恢复原始信号X,其数学模型[13]为
y=ФX
(1)
X∈RN×1,y∈RM×1,Φ∈RM×N
式中,y为测量值向量,即采样信号;Ф为观测矩阵;X为原始稀疏信号。
CS算法的实现包含3个必要因素:信号的稀疏表示、观测矩阵的构建和信号的非线性优化重构(在已知y、Ф的情况下利用重构算法恢复原始稀疏信号X)。CS算法框架如图3所示。

图3 CS算法框架Fig.3 Framework of compressed sensing
2.1 信号稀疏表示
CS算法模型要求原始信号X是稀疏的,而一般的时域信号都不是稀疏的,不能直接套用式(1),此时需要在稀疏基矩阵Ψ下将X进行稀疏表示。稀疏表示模型为
X=Ψθ
(2)
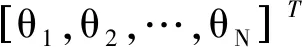
式中,Ψ为稀疏基矩阵;θ为稀疏系数矩阵。
将式(2)代入式(1)可得
y=ΦX=ΦΨθ
(3)
其中,若θ中仅有K个分量取值很大(K< 考虑测量噪声干扰时,y可以表示[14]为 y=ΦΨθ+η (4) η=[η1,η2,…,ηM]T 其中,为服从高斯分布的测量噪声序列。 由式(3)可知,观测矩阵Φ∈RM×N(M< M=O(Klog(N/K)),M< (5) 观测矩阵Φ在构建时需满足约束等距性条件(Restricted Isometry Property,RIP),即对于任意K-稀疏信号X和常数δK∈(0,1),满足[15]: (6) 式中,δK为约束等距常数(Restricted Isometry Constant,RIC)。 实际上,在处理非稀疏信号X时,式(1)中观测矩阵Φ满足RIP特性和式(3)中观测矩阵Φ与稀疏基矩阵Ψ满足不相干特性是等价的。因此相干系数定义[16]为 (7) CS理论指出[12]:若原始信号X是稀疏的或可以进行稀疏表示,并且观测矩阵Φ与稀疏基矩阵Ψ不相干,那么原始信号X可由测量值向量y求解l0范数下的最优化问题,从而以最大概率得到无损重构。l0范数的数学意义是表示θ中所有非零项元素的个数。重构过程[20]如下: (8) (9) 基于CS算法的矿井WSN目标定位方法,将矿井目标定位问题构建为CS算法稀疏信号重构问题。待定位目标是从测量值向量y中估计出位置信息向量θ,由式(3)中已知Ψ、Φ、y求取θ,所以该方法的关键问题在于Φ、Ψ和y的合理设计。 稀疏基矩阵Ψ的构建是在指纹法的离线阶段完成的。由文献[18]可知,稀疏基矩阵Ψ的元素取决于信号传播模型,而信号传播模型取决于井下电磁环境,针对某具体定位环境时,Ψ是相对固定的。 将矿井定位区域划分为N个网格并按序从1到N进行标号,定义Ψ为一个N×N维的稀疏矩阵,目标节点和参考节点按序放置在定位区域的网格内,参考节点需要对每一个网格内目标节点的接收信号强度值(RSSI)进行测量采样,网络模型如图4所示。 图4 目标定位网络模型Fig.4 Target localization network model 为更加准确地描述RSSI向量与空间位置的关系,构建完备的离线指纹库,每次假设参考节点位于1到N的每个网格内,N个参考节点对多个方向的目标节点分布进行测量,每个参考节点每次采集N个目标节点的RSSI值,每个RSSI值向量视为一个指纹,共采集N×N次,将每次采集到的RSSI值保存在矩阵Ψ中构建稀疏基矩阵,形成指纹库。Ψ中的行标为参考节点标号,列标为与之对应的网格序号。Ψ中的每个元素都是参考节点采集到的RSSI值向量,由此可得稀疏基矩阵Ψ[12]: (10) 观测矩阵Φ的构建是在在线监测阶段采用实时填写方式完成的,构建方法通常有3种:第1种方法根据实际接收到的信号强度值测量结果生成;第2种方法根据参考节点位置生成;第3种方法采用信号衰减模型生成。前两种方法更为简便实用,被广泛采用,本文采用第2种构建方法。 在离线指纹库建立阶段,为了构建完备的稀疏基矩阵Ψ,每个参考节点都会采集N个RSSI测量值,共N个参考节点,在线监测阶段则不需要烦琐的步骤,仅需M[M=O(Klog(N/K)]个参考节点随机布置在N个网格中,M< *—所在网格为参考节点的位置图5 定位区域参考节点布置Fig.5 Reference node layout of localization area 当第i个参考节点位于第j个网格内时,Φij=1;否则,Φij=0。因为有M个参考节点,所以Φ中共有M个非零值,每一行只有一个非零值。参考节点布置完成后,其位置相应确定,布置完成的网络观测矩阵Φ也确定,定义观测矩阵Φ为 (11) 由于观测矩阵Φ的元素值是非0即1的,故观测矩阵Φ和稀疏基矩阵Ψ相干。文献[22]指出,可对矩阵Φ、Ψ做正交化处理来满足RIP条件。 K个目标节点随机分布在不同网格内。由K< 其中,θ为N×1维向量,θ中元素的序号k对应网格的序号,求取目标位置,即为利用CS算法重构稀疏向量θ,确定θ中的非0元素的位置序号。 为验证本文所提出的CS算法应用在矿井WSN目标定位系统中的性能,本文实验采集的数据在Matlab 2013a软件上进行仿真。仿真计算机型号为戴尔Vostro 3667-R2848,CPU为I5-6400,显卡为NVIDIA GeForce 710 2GB,内存8 GB,硬盘1 TB,Windows10操作系统。 当参考节点数量M=20、目标节点数量K=10、网格数量N=1 000时,采用本文算法获得的定位结果如图6所示。由图6可知,CS算法重构出的目标位置与目标实际位置几乎完全重合,定位精度很高。实际应用中,定位精度与定位区域的网格划分面积有直接关系,网格划分的面积受矿井巷道长宽的影响。 图6 基于CS算法的矿井目标定位结果Fig.6 Localization results of mine target based on compressed sensing 将本文的CS算法与两种传统算法的定位误差比较,结果如图7所示。当参考节点数量M=20、目标节点数量K=10、网格数量N=1 000时,本文算法的定位误差可控制在0.8 m以内,比传统的指纹法定位误差(约1.17 m)提高了约33%,比基于TOA测距的三边法定位误差(约0.95 m)提高了约17.7%。由此可见,本文所采用的基于CS算法的矿井WSN目标定位方法,只要在线监测阶段实测信号强度测量值向量y包含目标位置信号足够的信息量,就可高概率恢复目标节点位置信号。 图7 定位误差对比Fig.7 Comparison of localization errors 当定位区域、参考节点数量M=20、目标节点数量K=10时,通过改变网格数量测试其对定位误差的影响。实验中将定位区域分别划分为N=100,200,…,1 000个网格,本文算法与两种传统算法的定位误差对比如图8所示。由图8可知,不论何种算法,只要定位区域、参考节点数量和目标节点数量不变,定位误差随着网格数量增多而减少,划分的网格数量越多,单个网格的面积就越小,定位精度就越高,定位误差就越小。当网格数达到1 000,即网格边长为1 m时,本文算法的定位误差趋于0.8 m,在3种算法中定位精度较高。 当定位区域、网格数量N=1 000、目标节点数量K=10时,通过改变参考节点数量测试其对定位误差的影响。实验中将参考节点数量分别布置为M=5,10,…,30,本文算法与两种传统算法的定位误差对比如图9所示。由图9可知,不论何种算法,只要定位区域、网格数量和目标节点数量不变,布置参考节点数量越多,接收到的有效信息越多,定位精度也就越高;但当参考节点达到一定数量时,定位误差反而出现增大趋势。这是因为布置过多的参考节点会增加定位复杂度,参考节点间的信号容易产生电磁波交叉干扰,导致接到的信息误差增大,不利于定位精度的提高。本文算法的参考节点数量必须满足式(5)的要求,在M=20时定位误差最小。 图9 参考节点数量对定位误差的影响Fig.9 Influence of reference node number on localization error (1) 本文将CS算法应用于矿井WSN目标定位系统中,建立两阶段定位方法:离线指纹库建立阶段和在线监测阶段。该方法仅通过少量参考节点测量目标节点信号强度值,便可通过重构算法恢复目标节点位置信号,求出目标节点位置。该方法减少了布置参考节点的工作量,降低系统的节点功耗和维护成本,证明本方法在煤矿井下目标定位的适用性。 (2) 本文算法的两阶段定位方法定位精度可控制在0.8 m以内,满足了定位需求。相比传统的定位算法,本文算法的定位误差最低,且定位误差随着网格数量参考节点数量的增加而降低;在其他条件不变的情况下,参考节点满足一定数量时,定位误差可达到最小,证明本文算法在煤矿井下目标定位的可行性。2.2 观测矩阵构建
2.3 信号非线性化重构
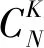
3 基于CS算法的矿井WSN目标定位
3.1 稀疏基矩阵Ψ
3.2 观测矩阵Φ

3.3 测量值向量y
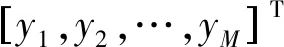
3.4 目标位置信息稀疏向量θ
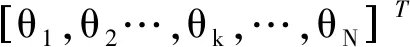
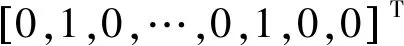
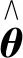
4 目标定位结果仿真分析
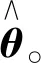
4.1 基于CS算法的定位误差
4.2 不同算法的定位误差对比
4.3 网格数量对定位误差的影响
4.4 参考节点数量对定位误差的影响
5 结 论
