两电平逆变器特定谐波消除的实时求解算法
2020-07-27王晨旭何飞张奇潘素娜杨克虎
王晨旭,何飞,张奇,潘素娜,杨克虎
1. 中国矿业大学(北京) 机电与信息工程学院,北京 100083;2. 奥尔堡大学,丹麦 奥尔堡 9220
采用特定谐波消除脉宽调制技术(Selected Harmonic Elimination Pulse Width Modulation,SHEPWM)可以精确地消除逆变器输出电压中选定的低次谐波。它具有开关频率低、输出电压质量高等优点,被广泛应用于各种大功率场合[1-3]。应用SHEPWM技术需要从一组非线性超越方程组(SHE方程组)中实时求解一个周期的开关角度,以实现系统的闭环控制。由于SHE方程组的非线性特性,开关角度的求解较为困难,目前常用的求解方法有数值法[4-6]、智能优化算法[7-10]、代数法[11-14]。
数值法主要包括牛顿法[4]、多项式同伦算法[5]、沃尔什函数法[6]等,这类算法具有一定的数学理论基础,易于实现,求解速度快,但对初值有依赖性,若初值选取不当会导致迭代时间长甚至发散。智能优化算法从随机解出发,按照遗传算法[9]、差分进化算法[10]等原理进行有限次迭代寻找最优解,这类算法对初值要求低、实现简单,但其数学基础薄弱,缺乏普遍意义上的理论分析,容易陷入局部最优解,无法保证其收敛性。代数法主要包括吴方法[11]、结式消元法[12]、Groebner基算法[13]等,这类算法通过数学理论对SHE方程组进行化简、消元,既不需要初值,又可保证求出全局最优解。但代数法的原理较为复杂,求解时占用的计算机内存多,难以在微控制器上实现。
上述方法均无法满足实际应用对开关角度求解的实时性、准确性和可靠性的要求。工业应用中常采用查表法[15]或人工神经网络法[16-17]来获取开关角度。查表法将离线求解的开关角度按照一定的抽样间隔存入微控制器中供程序实时查询。此方法需要占用大量芯片上的存储空间,当调制比位于采样间隔内时,需要通过插值近似确定开关角度,给控制系统引入一定的稳态误差。人工神经网络法使用离线训练的神经网络模型生成开关角度,具有较好的响应速度。神经网络毕竟是一种间接生成开关角度的方法,不能保证结果的准确性,虽然增加神经网络的规模可以提高准确度,但同时也会增加存储空间和计算时间。
为了克服现存方法的缺点,笔者提出了一种适用于微控制器的SHE方程组实时求解方法,该方法分为离线转换和在线求解两个阶段。离线转换阶段使用对称多项式和Groebner基理论对SHE方程组进行转换化简;在线求解阶段使用Sturm定理和数值法求解具体实根。此方法结合了代数法和数值法的优点,实现精确、高效的求解,具有以下优点:无须给定初值;占用计算资源少,可在微控制器中实现;求解效率高,满足控制系统实时性的要求;计算结果精确度高。基于此实时求解算法,本文搭建了两电平逆变器实验平台,验证了此算法的有效性。
1 SHE数学模型
图1为两电平逆变器拓扑结构。该拓扑由三个桥臂组成,分别对应输出三相交流电压;每个桥臂上下2个开关管交替导通,以实现交流电压输出;Udc为直流电源,R为负载电阻。
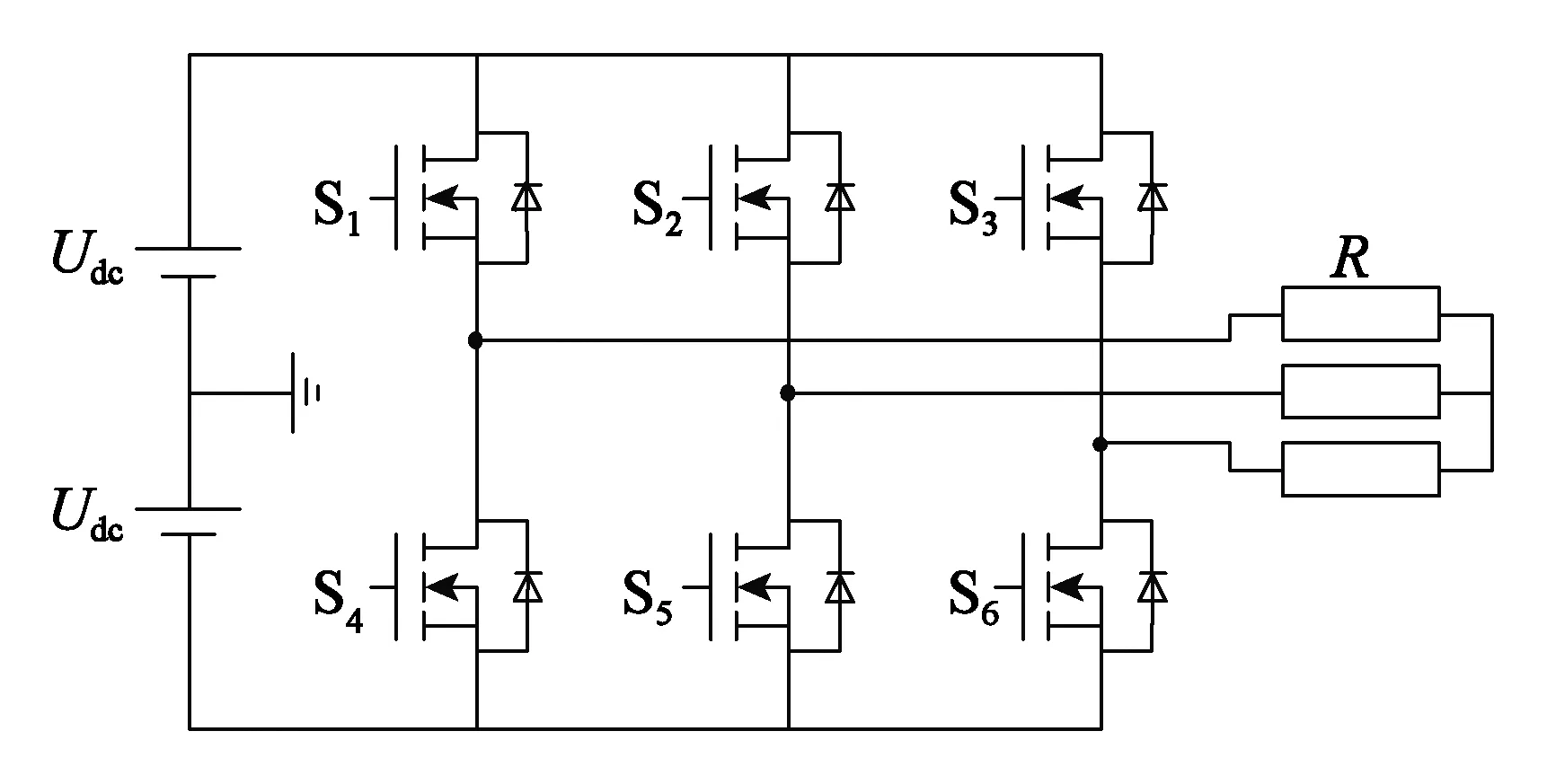
图1 两电平逆变器拓扑结构Fig.1 Topology of two-level inverters
两电平逆变器的输出相电压波形如图2所示。为了简化模型,通常假定PWM波形关于1/4周期偶对称、半周期奇对称。
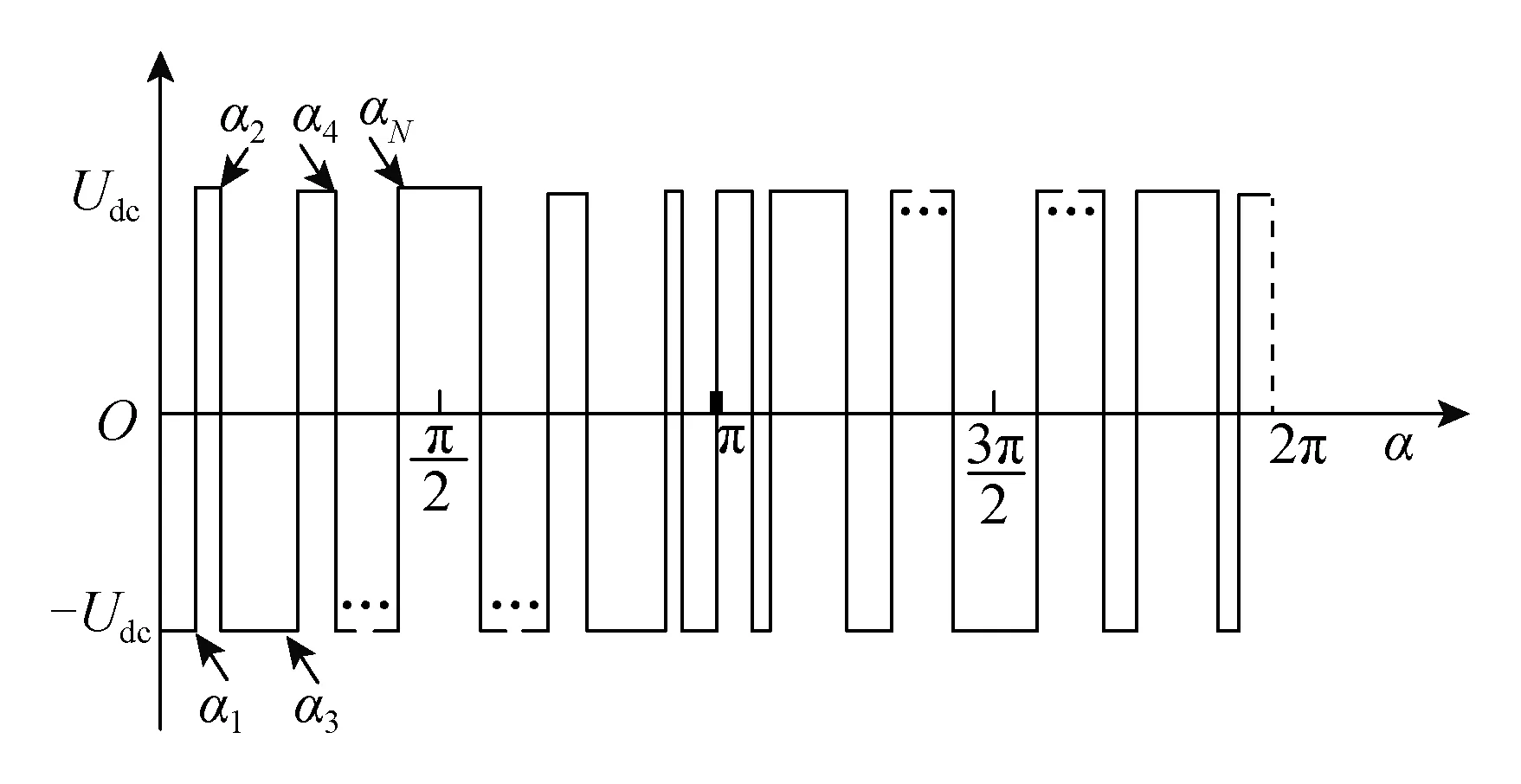
图2 两电平逆变器SHEPWM输出电压波形Fig.2 Output voltage waveform of two-level inverters
对图2中的波形进行傅里叶级数展开,可得各次谐波幅值与开关角度的关系:
(1)
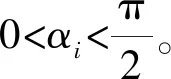
SHEPWM技术的基本思想是通过控制开关角度αi,输出期望的基波幅值,并使得某些特定次谐波的幅值等于零。以开关角N=5为例,在控制基波幅值的同时消除第3、5、7、9次谐波,根据式(1)得SHE方程组:
(2)
其中
式中,m为调制比。
调制比与基波幅值U的关系定义为
(3)
2 SHE方程组的离线转换
由式(2)可知,SHE方程组为非线性超越方程组,直接求解较为困难,利用对称多项式和Groebner基理论,可以将SHE方程组的求解等价转化为一个线性方程组和一个一元高阶多项式的求解[19-20]。
首先,对式(2)中的负余弦项应用变量代换αi=π-βi,使余弦项的符号统一为正号:
(4)
其中
采用三角函数倍角公式将式(4)展开,并作变量代换cosαi=xi,i=1,3,5,cosβi=xi,i=2,4,则SHE方程组被转化为一个对称的多项式系统:

其中
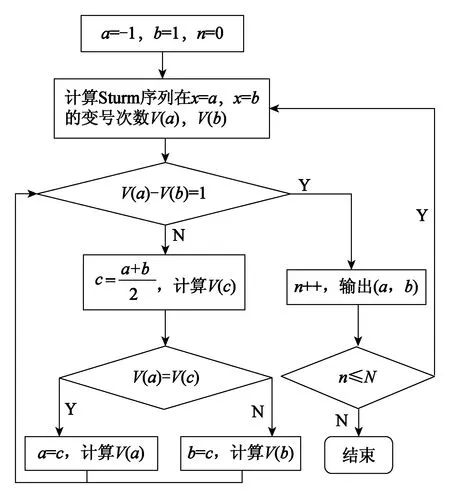
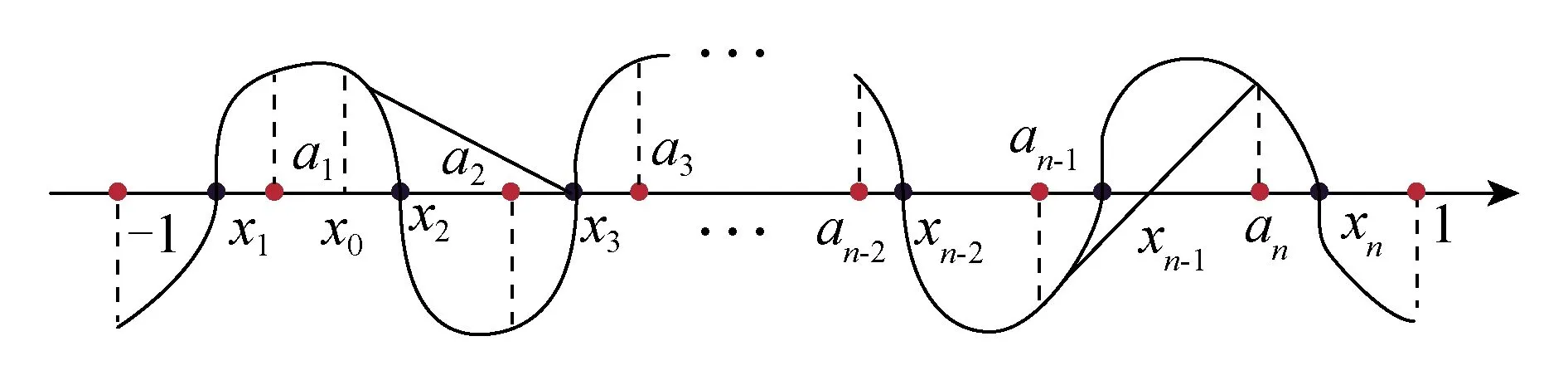
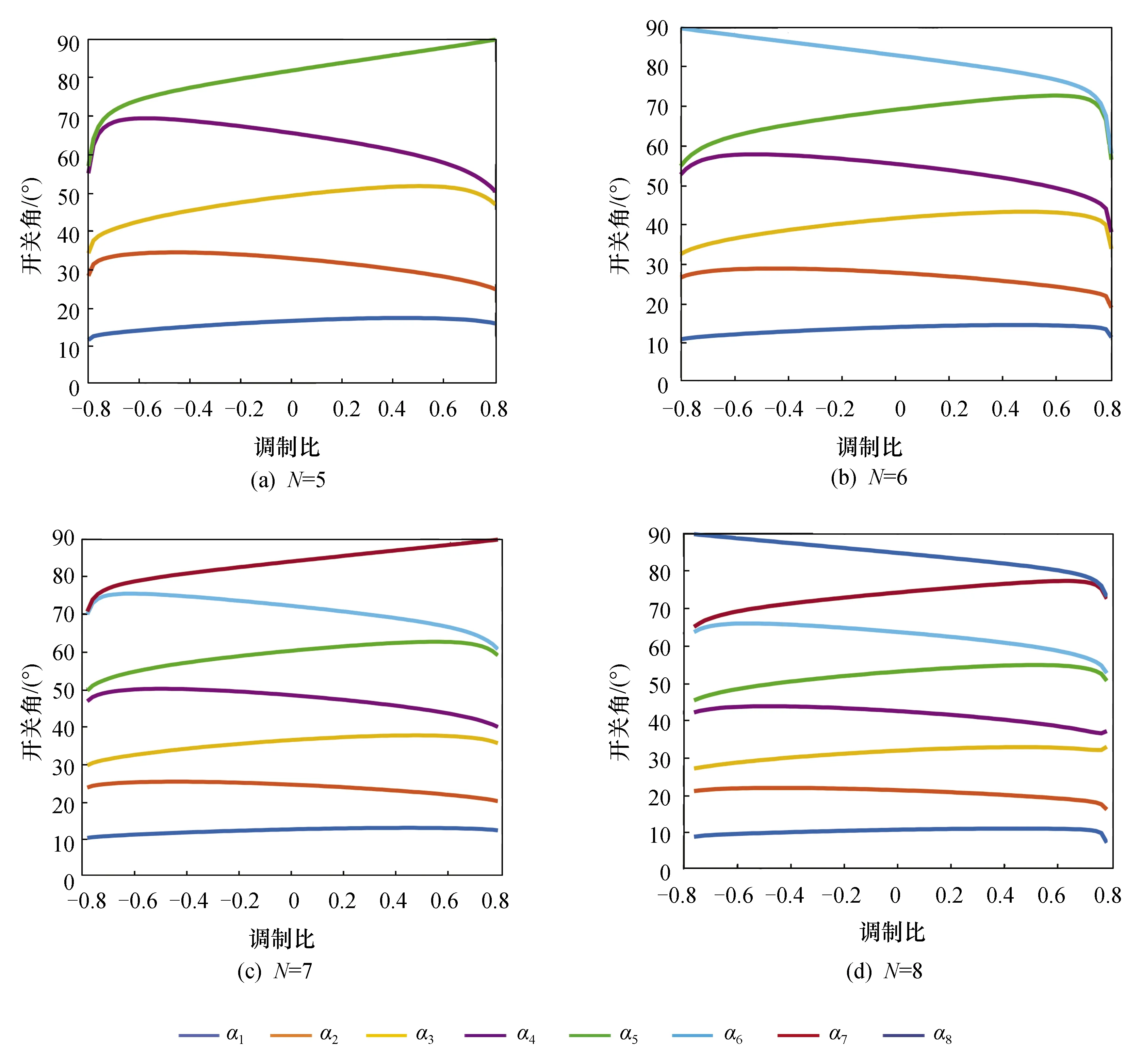
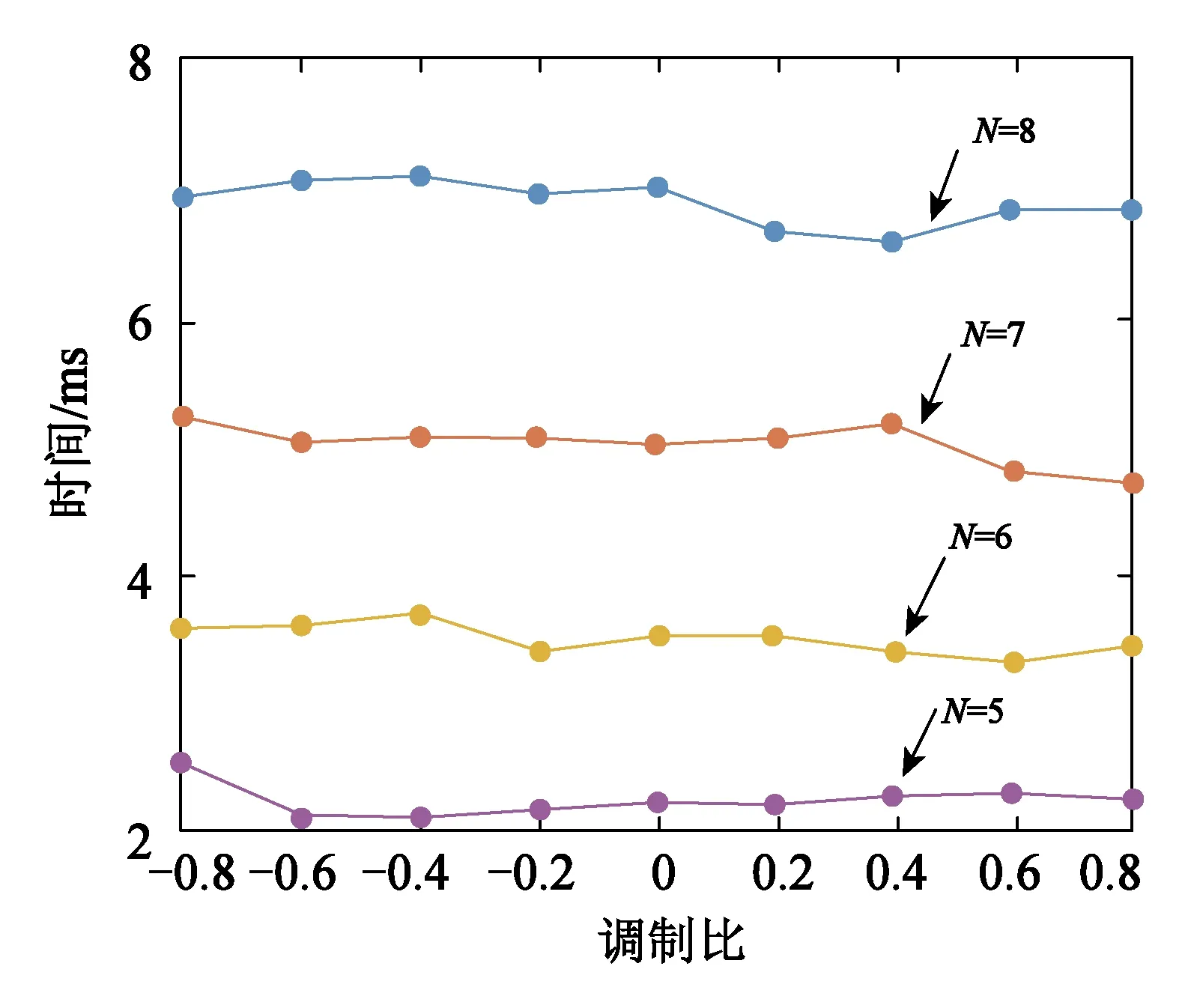
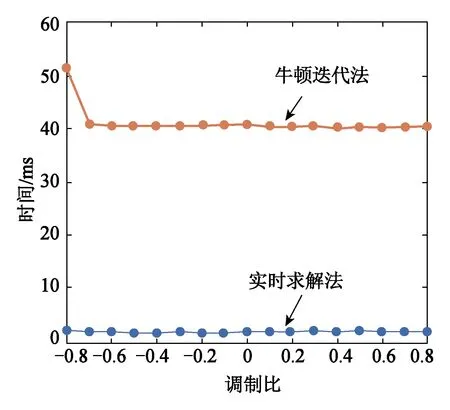
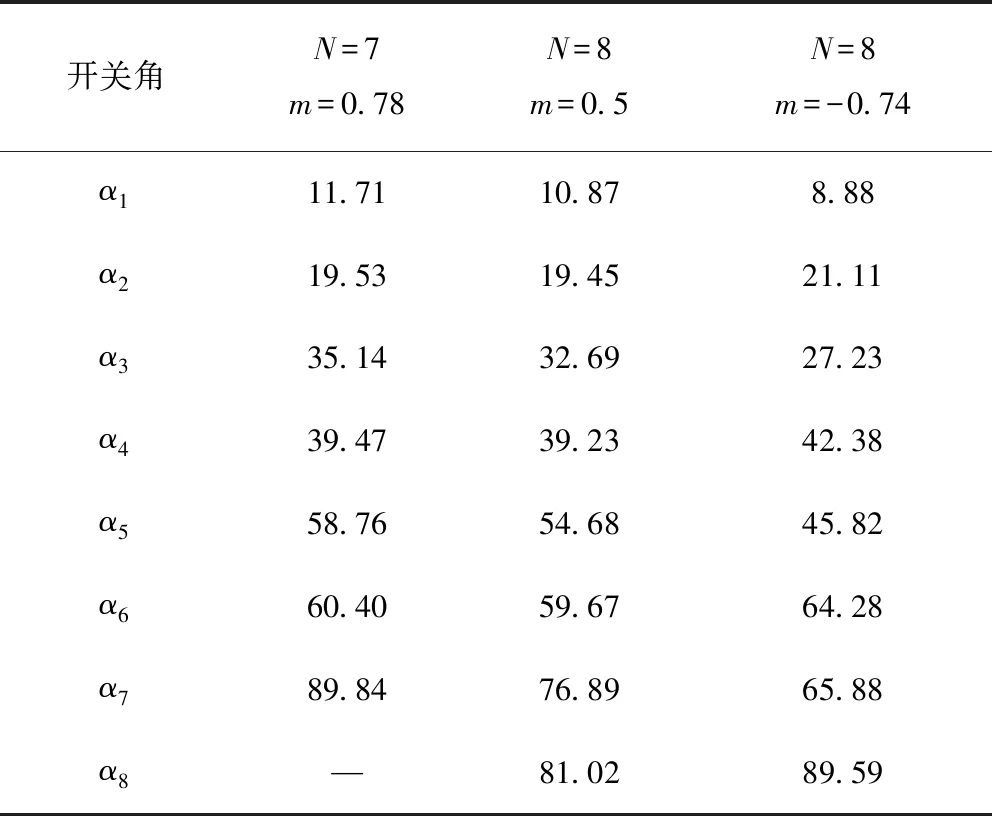
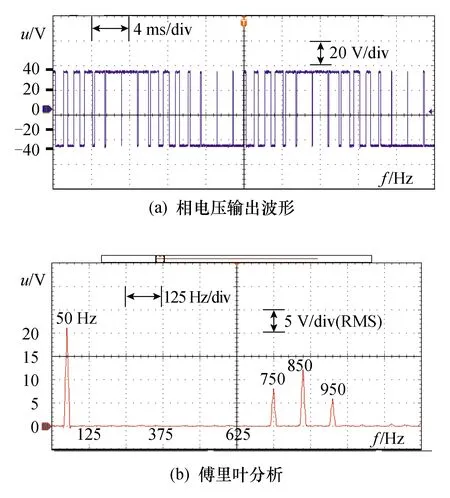
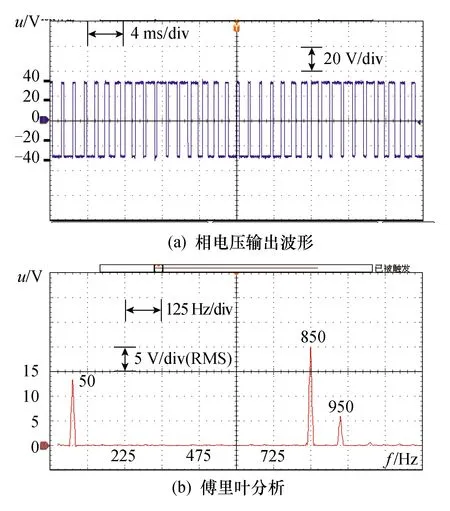
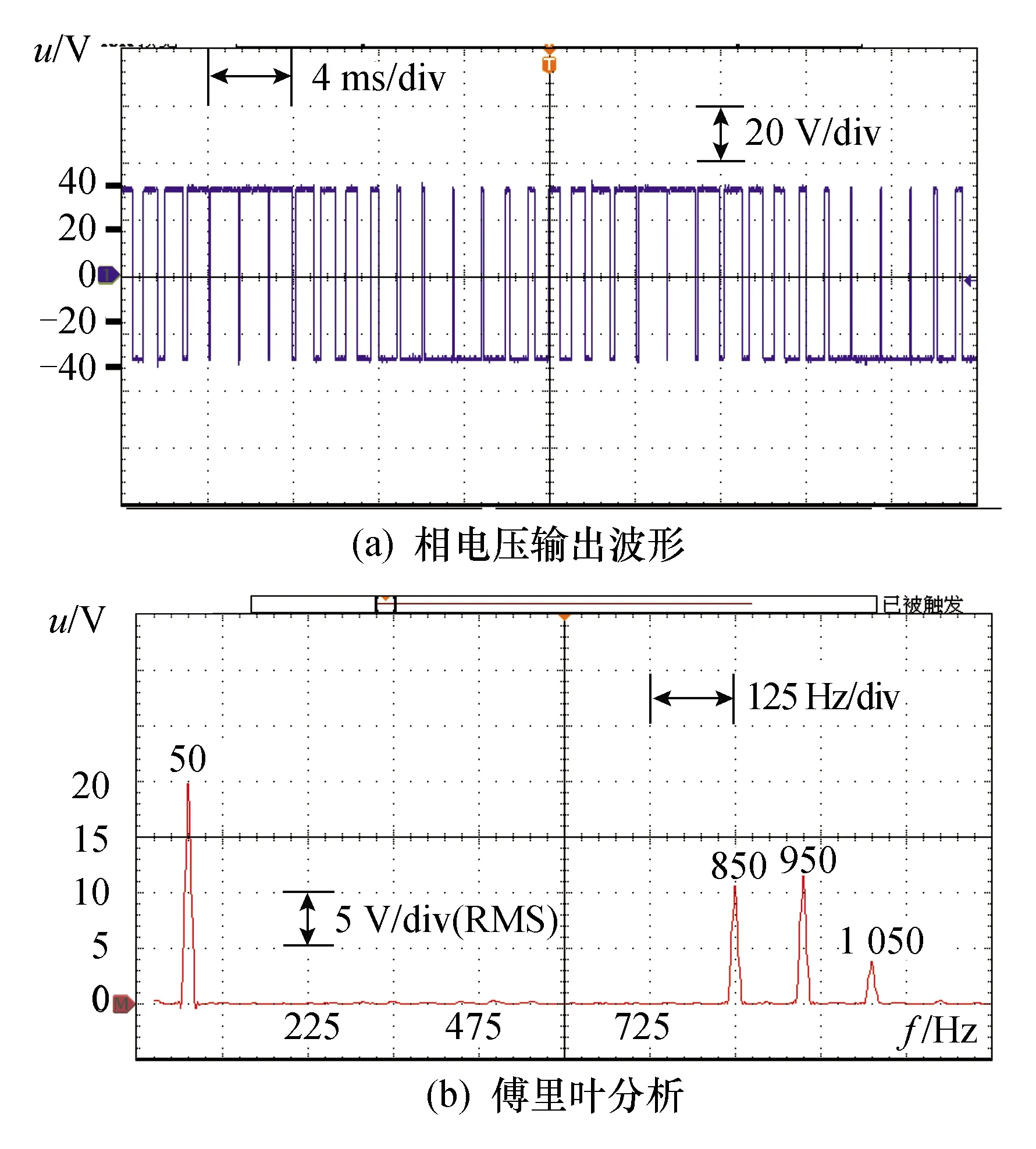
-1 式(5)为一个9次的多变元方程组,若使用代数法直接求解,随着开关角个数的增加,计算量和内存消耗会急剧增加。为了降低计算量,可使用初等对称多项式理论将式(5)化简降阶,详细的数学转换原理和推导过程可参考文献[13],这里仅作简要描述。 已知变元个数为5的初等对称多项式定义为 (6) 使用初等对称多项式将式(5)降阶,此过程可通过调用Mathematica软件中的Symmetric Reduction命令完成。由于式(7)中的表达式较长,故省略了中间部分: (7) f5(x)和f5(e)的阶次比较见表1。相比式(5),式(7)中变量的阶次得到了大幅降低,因此计算量也大大降低。 表1 f5(x)和f5(e)的阶次比较 进一步计算式(7)中多项式组的Groebner基[20],可以得到等价方程组: (8) 其中 A2=4m12-48m11+54m10+1 290m9-4 185m8- 9 180m7+47 250m6+14 175m5-198 450m4+28 350m3+340 200m2-42 525m-170 100 B2=36(m10-10m9+255m7-525m6-1575m5+ 4 725m4+1 575m3-9 450m2+4 725) A3=m13-13m12+12m11+462m10-1 515m9- 4 995m8+25 785m7+9 450m6-155 925m5+ 99 225m4+283 500m3-255 150m2-127 575m+ 127 575 B3=72(m10-10m9+255m7-525m6-1 575m5+ 4 725m4+1 575m3-9 450m2+4 725) A4=m14-14m13+7m12+672m11-2 226m10- 9 870m9+51 975m8+32 130m7-423 360m6+ 198 450m5+1 289 925m4-793 800m3- 1 786 050m2+595 350m+893 025 B4=1 008(m10-10m9+255m7-525m6- 1 575m5+4 725m4+1 575m3-9 450m2+ 4 725) A5=m15-15m14+945m12-3 150m11-18 270m10+ 97 650m9+99 225m8-1 091 475m7+ 396 900m6+5 060 475m5-4 465 125m4- 8 930 250m3+8 930 250m2+4 465 125m- 4 465 125 B5=30 240(m10-10m9+255m7-525m6- 1 575m5+4 725m4+1 575m3-9 450m2+4 725) 可见,e1,e2,…,e5单变元线性方程组中A2,B2,A3,B3,A4,B4,A5,B5是仅与调制比m相关的表达式。 需要指出,上述转化过程的运算量较大,需要在计算机中借助Maple或者Mathematica软件实现。离线转换结束后将方程组(8)存入微控制器中,以实现方程组的在线求解。 在线求解阶段,首先需要根据给定的调制比m求解方程组(8)得到e,然后根据e求解方程组(6)得到x,进而得到开关角度α。其关键和难点在于如何求解方程组(6)。文献[21]通过结式消元法将式(6)三角化后再迭代求解,具有转换过程复杂、中间变量多等缺点。本文利用一元高阶多项式根与系数的关系,将式(6)的求解转化为一元高阶方程的求解,然后利用Sturm定理[22]将一元高阶方程的实根隔离在不同区间,最后使用弦截法求出精确实根。 假设多项式f(x)的实根是x1,x2,…,xn,则f(x)的形式为 f(x)=(x-x1)(x-x2)…(x-xn) (9) 将式(9)展开得 f(x)=xn+e1xn-1+…+en-1x+en (10) 对比式(9)和式(10),多项式的系数与其实根具有如下关系: (11) 通过对比式(11)和式(6)发现,在已求得e的前提下,通过构造多项式方程有 f(x)=x5-e1x4+e2x3-e3x2+e4x-e5=0 (12) 由式(2)求出x,由多项式方程组(6)的求解转化为式(12)一元高阶方程的求解。当一元高阶方程的阶次小于等于4时,可直接使用求根公式求解;当阶次大于4时,可先找到若干互不重叠的区间,其中每一个区间包含一个实根,然后对每一个区间使用数值法求出精确实根。实根的隔离通常利用Sturm定理结合二分法完成,下面简要介绍Sturm定理。 设f(x)为实系数多项式,通过如下方式构造其Sturm序列: f0(x)=f(x)≠0f1(x)=f′(x)≠0f2(x)=-rem(f0(x),f1(x))≠0 ⋮fk+1(x)=-rem(fk-1(x),fk(x))≠0 ⋮fN(x)=-rem(fN-2(x),fN-1(x))≠0fN+1(x)=-rem(fN-1(x),fN(x))=0 (13) 式中,rem(fk-1(x),fk(x))为多项式fk-1(x)除fk(x)的余式;Sturm序列的前N项fi(x)≠0(i=0,1,2…,N)为f(x)具有N个实根;fN+1(x)=0为Sturm序列的结束。 Sturm定理:设(a,b)为任一区间,若f(a)f(b)≠0,则Sturm序列f0(a),…,fN(a)的变号次数V(a)与Sturm序列f0(b),f1(b),…,fN(b)的变号次数V(b)的差V(a)-V(b)恰好是f(x)在区间(a,b)内实根的个数。 应用Sturm定理,可以判断多项式在任意区间内的实根个数。由于式(12)的实根限定在区间(-1,1),将此区间不断二分,并对每一个区间使用Sturm定理判断其所包含的实根个数,直到找到N个互不重叠的区间且每个区间都包含一个实根。算法流程如图3所示。 图3 Sturm定理应用流程Fig.3 The flow chart of using Sturm theorem 根据Sturm定理得到多项式的所有实根区间后,可以用弦截法、牛顿法等[23]数值法求解方程的实根。由于每个实根的区间已经确定,需要保证求解时的迭代过程始终位于区间内。本文选用弦截法,而不是牛顿法。因为牛顿法在迭代过程中可能超出区间范围,造成求解失败。如图4所示,x2是方程在区间(a1,a2)内的一个实根,若选x0为初始值,牛顿迭代法将会错误地找到区间外的x3为根,造成求解失败。考虑上述情况,选择弦截法求解,如求解区间(an-1,an)内的实根时,弦截法以区间端点为弦,保证了所有的迭代过程均在区间内完成,非常适合当前的求解要求。 图4 牛顿迭代法与弦截法求根对比Fig.4 Comparison between the Newton-iteration method and the chord method 通过上述方法求解得到xi后,由三角函数反变换αi=arccosxi,i=1,3,5,βi=arccosxi,i=2,4得到开关角度,然后按照第2节所提到的方法进行最终开关角度的处理:αi=π-βi,i=2,4为下降沿;开关角为αi,i=1,3,5为上升沿。 以开关角个数N=5、调制比m=0.8为例,详细说明上述求解方法。 (1)将m=0.8代入式(8),可得: (14) (2)根据式(12)构造一元高次方程: f(x)=x5+0.1x4-1.311 36x3-0.064 802 6x2+ 0.383 773x+0.000 725 084 (15) (3)构造式(15)的Sturm序列: (16) (4)利用Sturm序列划分解的区间。把x=-1代入Sturm序列可得V(-1)=5: (17) 同理,把x=1代入Sturm序列可得V(1)=0: (18) 因此,方程在(-1,1)区间内含有5个实根,证明SHE方程组在该调制比下有解;然后使用二分法求出每个区间,计算结果如下: (-1.000 0,-0.750 0),(-0.750 0,-0.312 5),(-0.312 5,0.343 8),(0.343 8,0.671 9),(0.671 9,1.000 0) (5) 使用弦截法精确求解方程的根。对这5个区间使用弦截法迭代,得出5个具体实根为: -0.962 97,-0.684 6,-0.001 8,0.640 4,0.909 0;最后,将求出的5个根三角反变换,得到开关角度为:15.639°↑,24.626°↓,46.790°↑,50.171°↓,89.892°↑。 按照文中所述的过程绘制全调制比内的根轨迹图,如图5至图8所示。经计算,开关点数N=5、6时,SHE方程组在调制比在(-0.8,0.8)范围内有解;N=7、8时,SHE方程组在调制比在 (-0.79,0.79)内有解。开关点数正调制比表示基波初相位为0,负调制比表示基波初相位为π。 图5 不同开关点数时SHE方程组的解轨迹Fig.5 Roots locus map of SHE equations for different number of switching angles 图6为在STM32F407控制器上求解SHE方程组所需的时间曲线。当N=5时,在全调制比内所需的平均时间为2.25 ms;N=6、7时,所需的平均时间分别为3.5 ms和5.25 ms;在N=8时,所需平均时间约7 ms,基本满足控制器实时性需求。 图6 N=5、6、7、8时该算法的执行时间曲线Fig.6 Executing time curve of proposed method for N=5、6、7、8 图7为本文提出的实时求解算法与牛顿迭代法在STM32F407上的计算时间对比。传统的数值算法直接求解SHE方程组,而实时求解算法是将SHE方程组转化为一元高阶方程求解。由图7可知,牛顿迭代法所需的时间约40 ms,实时求解法所需时间约2 ms,求解速度提高了20倍。 图7 实时求解法与牛顿迭代法的计算时间对比Fig.7 Computation time of real-time method and newton-iteration method 为了验证本文提出的算法的有效性,搭建两电平逆变器实验平台如图8所示。 图8 两电平逆变器实验平台Fig.8 Experiment platform of two level inverter 控制芯片型号为ARM Cortex-m 3、处理器STM32F407,开关器件选用IPM模块STGIPS30C60,直流侧电压为30 V,输出的基波频率为50 Hz。 实验选取3组不同开关角个数与调制比进行验证,求解出的开关角度见表2。 表2 三组开关角 图9至图11为三组开关角的输相电压波形和傅里叶分析。由图可知,在N=7时,期望消去的第3、5、7、9、11、13次谐波均已消除;在N=8时,期望消去的第3、5、7、9、11、13、15次谐波均已消除。说明求解的开关角度是精确有效的。 图9 N=7,m=-0.78时的相电压 输出波形和傅里叶分析Fig.9 Output phase voltage waveform and FFT analysis for N=7,m=-0.78 图10 N=8,m=0.5时的相电压输出波形和傅里叶分析Fig.10 Output phase voltage waveform and FFT analysis for N=8,m=0.5 图11 N=8,m=-0.74时的相电压 输出波形和傅里叶分析Fig.11 Output phase voltage waveform and FFT analysis for N=8,m=-0.74 (1) 本文提出了一种适用于微控制器的开关角实时求解方法,在STM32F407处理器中求解5个开关角所需时间为2.25 ms,求解8个开关角所需时间为7 ms,与牛顿迭代法相比,速度提升了20倍。 (2) 该方法很好地解决了传统数值算法需要给定初值、智能优化算法和代数法计算量大等缺陷,具有数学理论基础完备、求解精确度高等优点。 (3) 实验结果显示,利用该方法所求出的开关角能够精确地控制基波幅值,同时可以消除指定的各次谐波,验证了算法的正确性与有效性。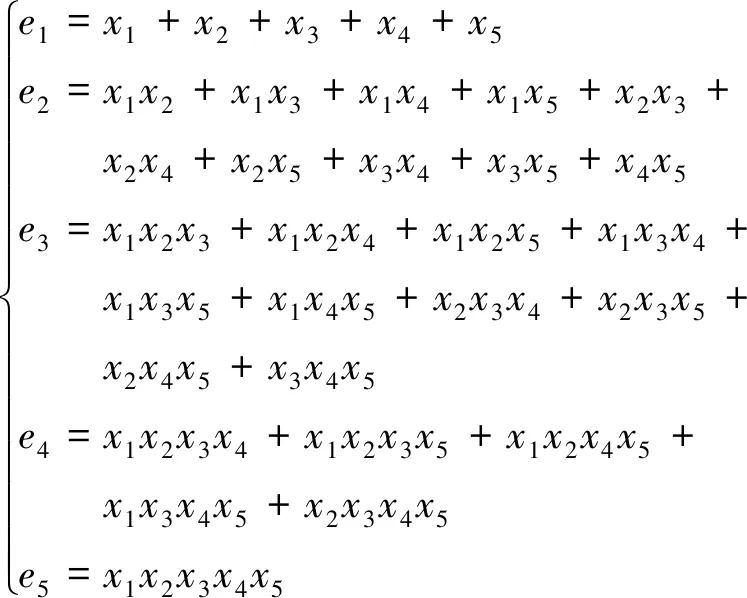

3 SHE方程组在线求解
4 计算案例与结果分析
4.1 案 例
4.2 全调制比内的求解结果
4.3 实时性分析
5 实 验

6 结 论
