基于局域栅格化的履带支护车自主导航方法研究
2020-07-27李瑞张敏骏王鹏江沈阳吴淼
李瑞,张敏骏,王鹏江,沈阳,吴淼
1. 中国矿业大学(北京) 机电与信息工程学院,北京 100083;2. 清华大学 机械工程学院,北京 100084
履带式行走机构已被广泛应用于军事作战、矿山设备等领域[1]。履带支护车作为典型的履带式行走机构可与掘进机、自移式临时支架配套使用,是煤矿综掘工作面的核心装备[2]。在煤巷实际工况环境中,履带支护车会因底板的不同地质条件而引起滑转率误差和掘进机位姿不固定等,导致在作业中面临受限巷道空间内的航向纠偏难题。在我国综掘巷道自动化与智能化程度仍处于较低水平的现状下[3],要完成受限巷道空间内履带支护车的路径自主导航,实现煤巷顶板的快速有效支护,满足综掘巷道自动化与智能化发展需求,这对工程实践具有指导意义[4-6]。
煤巷底板地质条件较为复杂、环境封闭,履带支护车的自主导航需要在确定环境参数与工况约束的前提下实现[7]。因此,需要完成巷道内工况场景建模,并构建合理的自主导航控制方法才能满足实践需求[8]。秦玉鑫等[9]提出了一种模块化的局部栅格地图表示方法,通过使用TOF相机获取环境信息,形成三维点云坐标矩阵,实时解算局部栅格地图并创建全局环境栅格地图;徐雪松等[10]采用栅格法进行了工作环境建模,通过螺旋控制信息搜寻并启发改进动态差分进化算法,实现了机器人的路径优化;周俊静等[11]以激光雷达作为传感器分别提出不同的运动目标检测方法。采用上述文献中所涉及的栅格地图构建方法进行二维场景模型的区域划分是目前工程实践较为认可的场景构建模型的方法。
煤巷井下采掘设备进行位姿检测与定位存在偏向位姿误差,即航向角与偏距[12]。自主导航是从当前的车体位姿进行实时检测,并解算规划向目标位姿调整而形成的航向路径。李云伍等[13]提出了基于RTK-GNSS路网信息采集、实时定位和路径规划的丘陵山区田间道路上自主行驶与视觉导航系统;陈燕等[14]基于模糊控制思想,应用加权因子控制器提高了PID控制对喷播机恒速液压转向系统的响应速度;韩庆钰等[15]在履带车的路径跟踪算法中引入线速度与角速度作为中间变量,从而避免了系统失稳,并提高了履带车路径跟踪算法的快速性与稳定性;Lin 等[16]基于立体视觉检测技术,提出了水下无人车辆路径优化算法。但由于煤巷综掘环境中履带支护车的运动方式、受限条件均特殊,上述文献的路径导航优化方法无法完全适用于履带支护车的特殊工况环境。
因此,笔者基于煤巷底板的土壤力学模型,提出了航向参考影响度的概念公式,减少了栅格化场景中因子数量,降低复杂工况环境对系统模型造成的多重影响。通过履带支护车的液压行走系统数学建模与验证分析,验证其闭环系统的稳定性,并设计了模糊PID控制器,对履带支护车作业路径的航向角进行实时纠偏和仿真验证。
1 工况场景构建
1.1 自移式超前支护装备简介
自移式超前支护装备机械系统[17]主要包括自移式临时支架、履带支护车以及辅助部件等。其中,自移式临时支架用于综掘巷道的顶板支护;履带支护车可携带自移式临时支架由巷道后方驱动,骑跨式越过掘进机与桥式转载机将支架运送至综掘工作面。自移式超前支护装备的作业原理如图1所示。
自移式超前支护装备的作业工艺流程:位于煤巷综掘工作面前方的掘进机进行掏槽、断面截割,巷道后方已完成永久锚固的自移式临时支架卸荷、收缩并降落到履带支护车的顶梁链传动机构上,通过履带支护车驱动骑跨式越过带式输送机、桥式转载机与掘进机,最终将自移式临时支架运送至综掘工作面端头,自移式临时支架进行工作面端头的顶板有效支护,然后履带支护车撤回到掘进巷道后方预备下一周期的支架运送。
1.2 巷道栅格化建模
履带支护车的工作环境为存在封闭边界的煤岩体隔离空间,巷道底板不同地质条件对于车体行进的影响十分关键。面对复杂路况与受限巷道空间的影响与制约,借鉴传统移动机器人路径规划中栅格化思想构造受限巷道空间内的场景模型。
如图2所示,以巷道水平中心轴线OA为X轴,垂直于OA的直线为Y轴,建立水平直角坐标系。B、C、D作为履带支护车在行进过程中巷道底板介质成分未知的复杂路面,称为受限空间内的非常规路况区域。经过该区域在OXY平面内的投影中心点,分别作X轴垂线段,得到直线集合簇{L1,L2,…,Ln}可将受限巷道空间划分为多个平面栅格化区域。
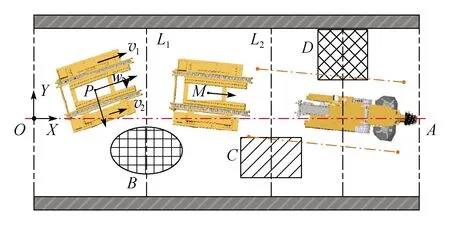
图2 局域栅格化巷道模型Fig.2 Model of roadway in regional grid
将受限巷道空间内每个非常规路况区域的面积定义为S,其中心点到X轴的纵高为H,到Y轴的横深为L。考虑每格非常规路况区域对于履带支护车航向角的影响程度不同,提出对于履带支护车的航向参考影响度I的概念公式为
(1)
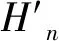
履带支护车作为大型矿山作业器械,自身具备一定抗干扰能力,过多的参数与高维度变量会对其自主导航模型增加不必要的难度。因此,基于巷道底板路况信息的栅格地图的格数划分由受限空间内的非常规路况数量决定。以航向参考影响度为基准阈值,基于履带支护车的运动特征计算不同工况环境影响航向角的参考值,忽略小于此基准阈值的非常规路况区域,最终实现模型的简化。
1.3 工况影响因子分析
为进一步提高受限巷道空间内栅格化场景模型的精准性,需要进行巷道底板的土壤力学特性分析,从而得到煤巷底板不同地质条件下履带支护车的滑转率参数,以提高航向参考影响度计算公式中数据获取的可信度。
对于一般的履带式行走机构,需做3点假设:① 履带接触地面部分始终与底板保持紧密接触;② 履带接地压力沿地面分布;③ 履带链齿两侧产生的附加驱动力可忽略不计。
依据Bekker 提出的压力-沉陷关系理论[18]与Wong 提出剪切应力理论[19],履带驱动力为
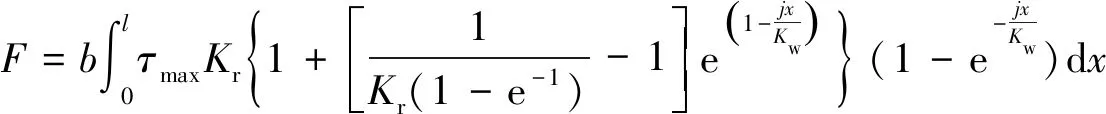
(2)
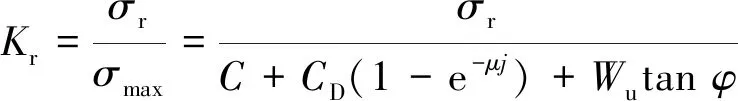
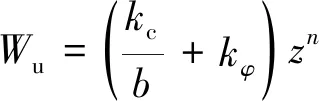
式中,Kw为最大剪切应力对应的剪切位移,m;Kr为剪切应力与最大剪切应力的比值;C为剪切强度,kPa;CD为土壤常数;μ为地面阻力系数;φ为土壤内摩擦角,(°);Wu为法向应力,kPa;kc为土壤黏聚变形量,kN;kφ为摩擦变形模量,kN;b为测量剪切板宽度,m;z为沉陷量;n为沉陷指数;j为剪切位移,m。
(3)
式中,Sz为履带接地面积,m2;c为地面黏着系数;M为履带支护车质量,kg。
履带支护车在综掘巷道中行进时,其两侧履带的滑转率为
(4)
式中,K为地面剪切变形系数;Lh为履带接地长度,m;F′为履带牵引力,N。
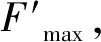
2 自主导航运动模型
履带支护车行进速度较为缓慢,且属于大质量大惯性体器械,因此履带支护车在转向导航过程中由向心力引起的测向打滑可以忽略不计。同时受到巷道底板路面以及其他因素的影响,履带支护车在完成自主导航前必定存在一定的偏差。将受限巷道空间内履带支护车的自主导航运动定义在平面二维直角坐标系中,其简化模型如图3所示。
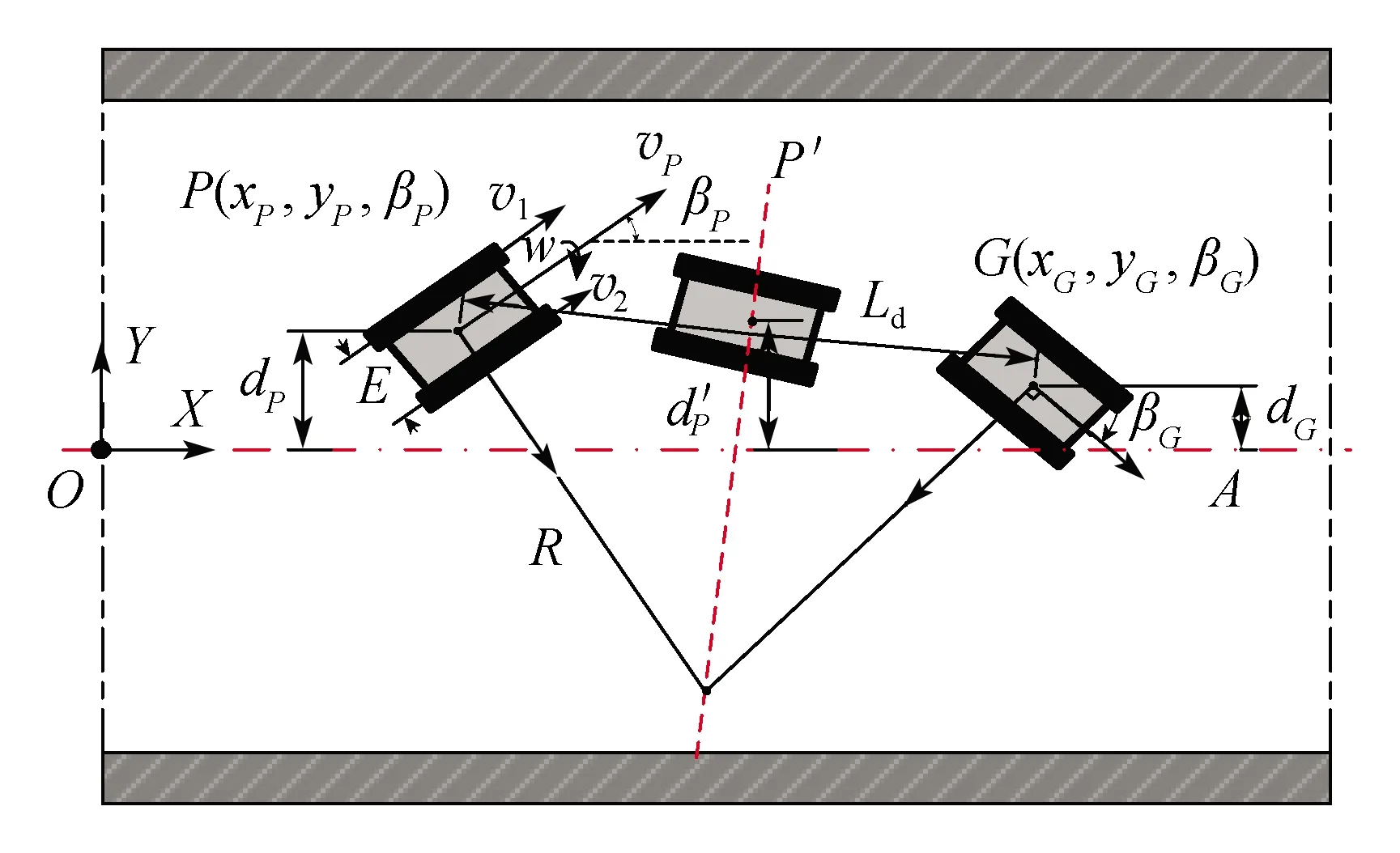
P—履带支护车的初始位姿点;G—履带支护车的期望位姿点;R—履带支护车的转向半径;E—履带支护车的履带中心轴距;dP—点P垂直于巷道X轴线的偏距;dG—点G垂直于 巷道X轴线的偏距;Ld—点P与点G之间的直线距离图3 履带支护车的导航简化示意图Fig.3 Simplified navigation diagram of crawler support vehicle
由图3可知,履带支护车航向偏差变化率为
(5)
式中,βP为履带支护车在点P相对于巷道X轴线的航向角,(°);βG为履带支护车在点G相对于巷道X轴线的航向角,(°);wP为履带支护车在点P的转向角速度,rad/s;wG为履带支护车在点G的转向角速度,rad/s;vP为履带支护车在点P的转向速度,m/s;vG为履带支护车在点G的转向速度,m/s。
履带支护车在初始位姿点P的速度为
(6)
式中,v1、v2为履带支护车外内侧履带理论速度,m/s。
履带支护车自主导航采用差速式转向,其实际转向半径R与内外两侧履带速度满足关系式为
(7)
式中,i1为履带支护车内侧履带差速转向时所接触煤巷底板地质条件的滑转率;i2为履带支护车差速转向外侧履带接触煤巷底板地质条件的滑转率。
基于测绘原理与几何关系可知,履带支护车的理想转向半径R′与其位姿参数满足关系式为
(8)
履带支护车的初始位姿(xP,yP,βP)与期望位姿(xG,yG,βG)可通过成熟的煤巷井下车体位姿测量技术得到[20-21]。履带支护车从初始位姿到期望位姿的航向角变化量为Δβ=βP-βG,偏距变化量为Δd=dP-dG。履带支护车进行导航任务前期,将各个传感器测得位姿参数信息经过连续电路与数模转换器传输至单片机进行解算,得到履带支护车的期望转向半径R满足Δd=0, Δβ=0,Ld=0。履带支护车进行导航任务过程中,在跟踪直线Ld趋近于零时可能有2种情景:① Δd=0且 Δβ≠0,此时履带支护车需通过绕车体自身中心回转进行航向角调控,实现Δβ=0;② Δd≠0且 Δβ=0,此时履带支护车需进行直线行驶并保持双履带同速控制,实现Δd=0。
实时检测解算履带支护车的实际转向半径R′,并将其作为期望转向半径,通过控制器与回路连接履带支护车的液压行走系统进行速度调控,实现履带支护车在受限巷道空间内的航向智能纠偏。
3 模型构建与验证
履带支护车的液压行走系统是由变量泵、定量马达、电液比例方向流量阀、补油泵、冲洗阀、安全阀、控制器、其他液压元件以及相应的传感器等部件组成。闭环控制回路中的控制信号通过检测泵控马达的转速差控制变量泵的斜盘转角,从而改变流量,使马达的转速差达到预期效果。
3.1 系统构建
将速度传感器视为一个比例控制项,其传递函数为
(9)
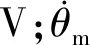
比例放大器的频带宽度远高于比例方向流量阀的频带宽度,因此其传递函数可表示为比例放大器输出电流与系统电压之比为
(10)
式中,Kα为比例放大器增益,A/N;Ia为比例放大器的输出电流,A;Ua为比例放大器输入电压,V。
比例方向阀具有快速的动态响应及良好的静态特征,适当忽略阀内油液可压缩性的影响,将其理想化为滑阀,得到电液比例方向阀增益为
(11)
式中,Kdj为比例方向阀增益,m/A;Xj为比例方向阀阀芯位移,m;I为电液比例方向阀输入电流,A。
液压缸的传递函数则可近似用积分控制项与比例控制项的乘积来代替[22],即
(12)
式中,Xq为液压缸活塞位移,m;Kvj为比例方向阀在稳态点流量增益,m3/s;Aq为液压缸有效受压截面积,m2。
在变量泵控马达系统中,变量泵的斜盘机构与回转机构起到排量调节作用,其原理可满足
Xq(s)=Lqsinφ(s)≈Lqφ(s)
(13)
式中,Lq为液压缸受力点到斜盘铰点之间的距离,m;φ为变量泵斜盘倾角,rad。
变量泵的输出流量方程为
Qt(s)=Ktφ(s)-CtpA(s)
(14)
式中,Qt为变量泵的输出流量,m3/s;Kt为变量泵的流量增益,m3/s;Ct为变量泵的总泄漏系数, m5/(N·s);pA为变量泵出口端压力,kPa。
液压马达高压腔流量方程为
(15)
式中,Qm为马达的输入流量,m3/s;θm为液压马达的转角,rad;Dm液压马达的弧度排量,m3/rad;V0包括变量泵与液压马达高压腔及高压管路总容积,m3;Ctm为液压马达的总泄漏系数,m5/(N·s);βe为液压马达有效体积弹性模量,kPa。
马达与负载的力矩平衡方程为
DmpA(s)=(Jms2+Bms+KF)θm(s)+TL(s)
(16)
式中,Jm为马达和外载荷折算到马达输出轴上的总转动惯量,kg·m2;Bm液压马达和外载荷折算到马达输出轴上的黏性摩擦系数,N·m·s;KF为负载的扭转弹簧刚度,N·m/rad;TL为任意外负载力矩,N·m。
结合式(14)至式(16)消去中间变量,可得马达转角位移量θm的输出方程为
(17)
式中,Vt为液压缸工作容腔,m3;Cts为泄漏系数总和,m5/(N·s)。
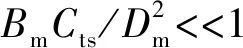
(18)
式中,ωh为液压缸固有频率,Hz;ξh为液压阻尼比。
综上可得履带支护车液压行走控制系统的方框图,如图4所示。

图4 履带支护车液压行走控制系统的方框图Fig.4 Block diagram of hydraulic walking control system of crawler support vehicle
由图4可得履带支护车液压行走系统的开环与闭环传递函数为
(19)
(20)
3.2 模型验证与分析
为验证被控对象的数学模型有效性,首先对履带支护车液压行走系统中的各元器件进行资料查阅,选取基于实际工况环境的模型参数并计算其他间接参数,根据开环系统的伯德图(Bode)与奈斯特图(Nyquist)对该系统进行稳定性分析。
参考相关设备并结合实际工况需求,履带支护车液压行走控制系统的参数取值如下:比例放大器增益Kα=0.2 A/N;比例方向阀增益Kdj=0.251 m/A;比例方向阀在稳态点流量增益Kvj=0.174 m3/s;变量泵的流量增益Kt=8.51×10-3m3/s;液压缸有效受压截面积Aq=3.14×10-2m2;液压马达的弧度排量Dm=104m3/rad;液压缸受力点到斜盘铰点之间的距离Lq=100 mm;液压缸固有频率ωh=4 rad/s;液压阻尼比ξh=0.9;比例控制项增益Kf=0.13 V·s/rad。
根据上述参数,履带支护车液压行走系统的开环与闭环传递函数为
(21)
(22)
依据式(21)编写 Matlab 程序,绘制履带支护车液压行走系统的开环伯德图与奈斯特图(图5)。
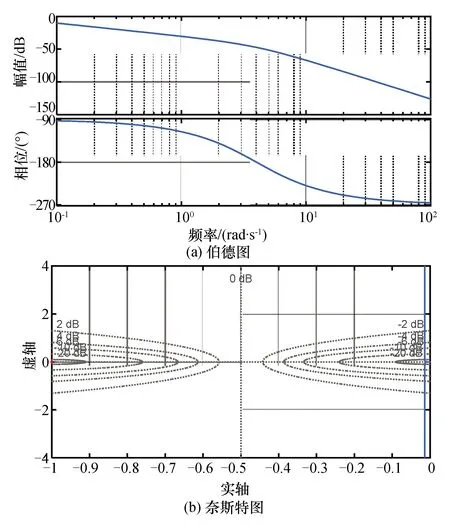
图5 系统伯德图与奈斯特图Fig.5 Bode and Nyquist plots of the system
由图5(a)图可以计算出履带支护车液压行走系统的开环传递函数的幅值裕度Gm=232.258 dB,相位裕度Pm=89.201°,两项均大于零,因此所建立的履带支护车液压行走系统是相对稳定的。
3.3 控制器设计
基于系统的非线性考虑,采用模糊PID算法的目标是使比例、积分与微分3种PID控制参数达到最佳配比,以满足实际工况需求[23]。履带支护车自主导航控制系统结构原理如图6所示。
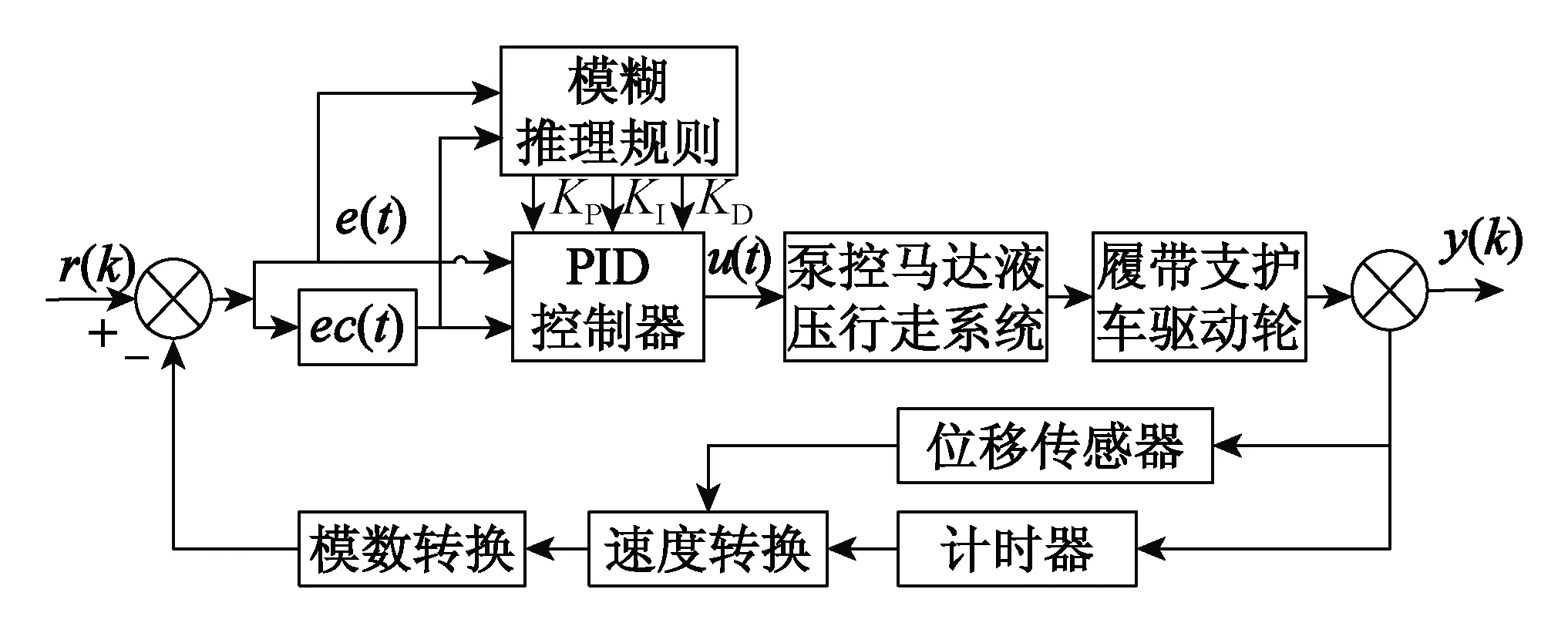
r(k)—k时刻期望履带驱动速度;y(k)—k时刻履带实际速度图6 履带支护车自主导航控制系统结构Fig.6 Control system of the autonomous navigation
由图6可知,期望履带速度r(k)与实际履带速度y(k)的差值e(t)及其变化率ec(t)作为模糊PID控制器的输入变量。其与输出量u(t)之间的关系满足
(23)
式中,KP为比例增益;KI为积分增益;KD为微分增益。
采用二维模糊控制器,输入已确定为e(t)及其变化率ec(t),输出为3个修正参数ΔKP、ΔKI、ΔKD,调整规则如下:
(24)
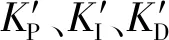
偏差量e(t)和偏差变化率ec(t)的基本论域均为[0,6],修正参数的基本论域均为[-3,3],划分7个语言变量分别为{NB,NM,NS,ZO,PS,PM,PB},对应7个模糊子集为{负大,负中,负小,零,正小,正中,正大}。模糊推理过程设置:模糊控制器采用Mamdani算法,解模糊清晰化方法为面积中心法,2个输入与3个输出的隶属度函数均采用三角函数隶属度函数;PID调节器的参数预设初始值采用临界比例度法最终确定为1.5、1.1、0.15。
结合专家经验与自整定原则,归纳偏差量e(t)、偏差变化率ec(t)和修正参数ΔKP、ΔKI、ΔKD之间的关系,见表1。依据表1所设置的控制规则,通过模糊控制器模糊化、近似推理与解模糊清晰化处理后,把得出的修正量ΔKP、ΔKI、ΔKD分别输入到PID调节器中,实现对于3个控制参数的实时在线修正,从而达到预期的控制效果。
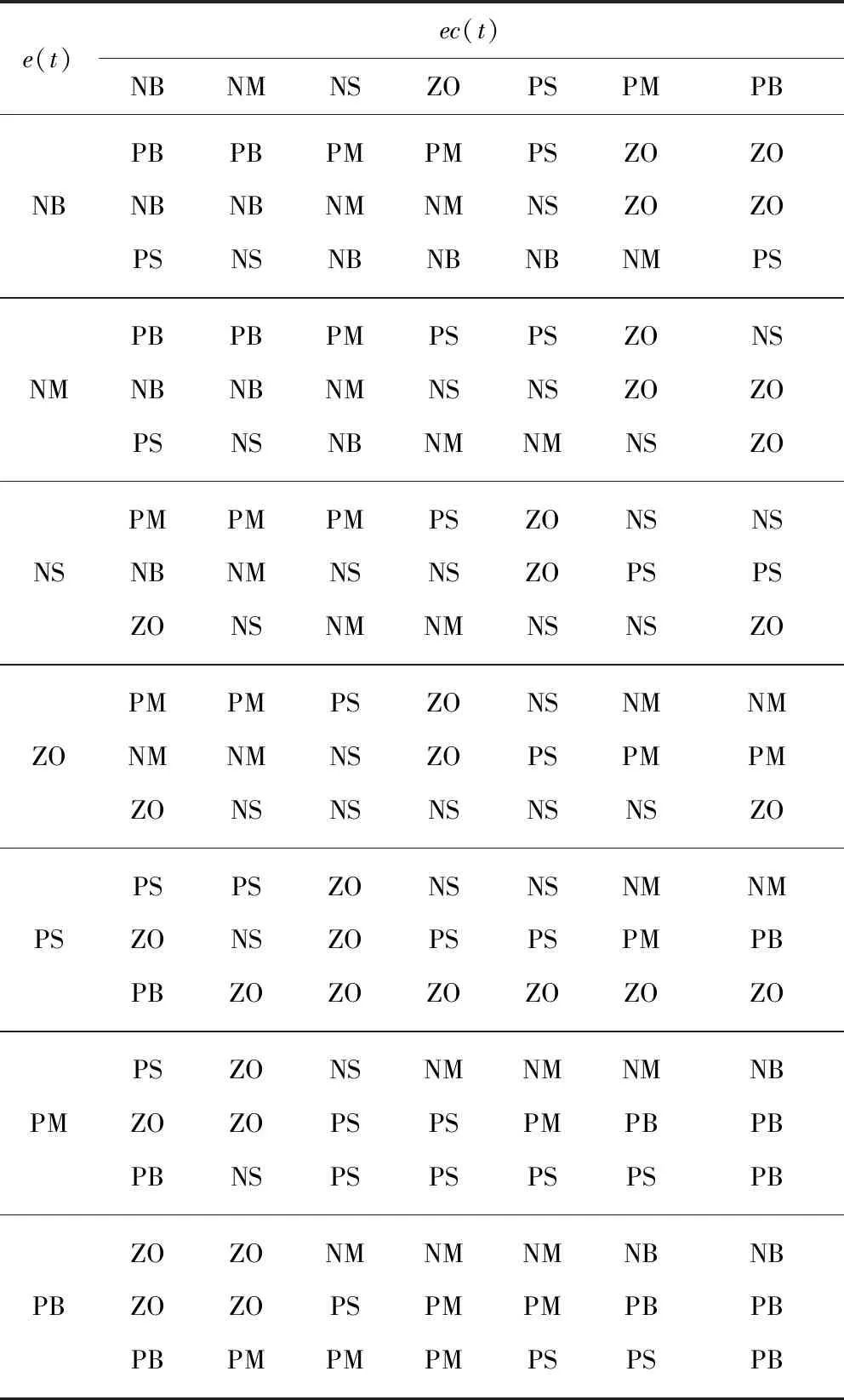
表1 模糊控制规则
4 仿真试验与分析
4.1 模型建立
以石家庄煤矿机械有限责任公司研制的CZL-45型履带式支护车为基础对象,车体相关的参数见表2。综掘巷道中不同的底板路面滑转率参数与土壤地质参数见表3。
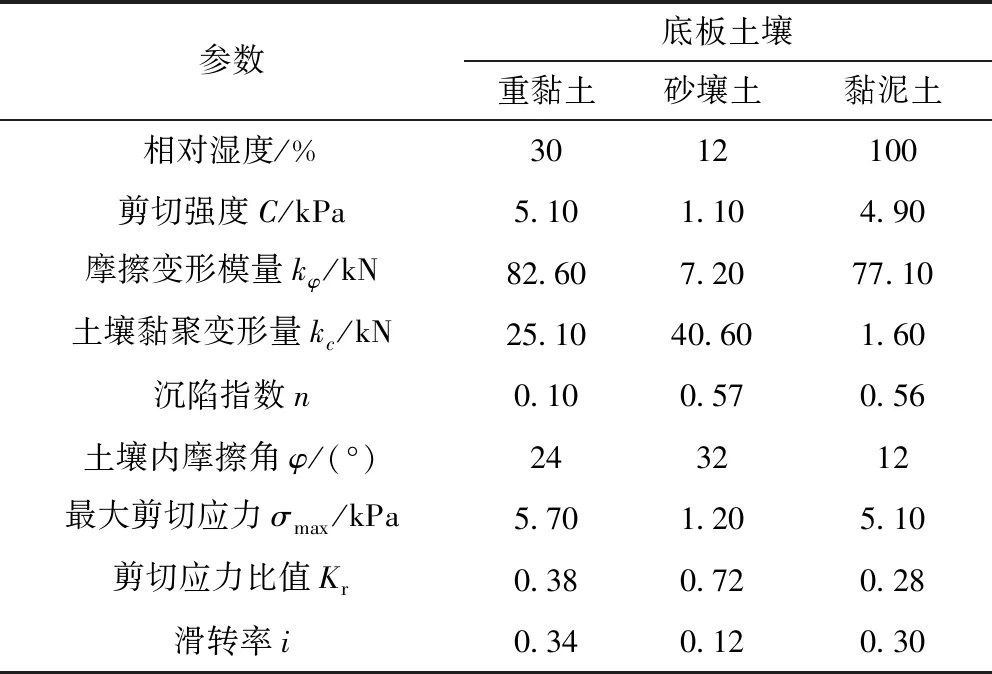
表3 煤巷底板路面地质参数Tab.3 Soil parameter of coal roadway floor pavement

表2 履带支护车主要参数
由于液压系统在实际工作中存在很多不确定因素[24],若直接将式(22)在Matlab环境中建立仿真模型,会给仿真带来一定的不精确性,故采用在AMESim与Matlab/Simulink联合环境下进行仿真。首先在AMESim中建立履带支护车液压行走系统的半实体物理仿真模型,在Matlab/Simulink中建立模糊PID控制器,通过Interface Block模块实现情景交互,最终建立履带支护车液压行走系统的半实体物理联合仿真模型(图7)。
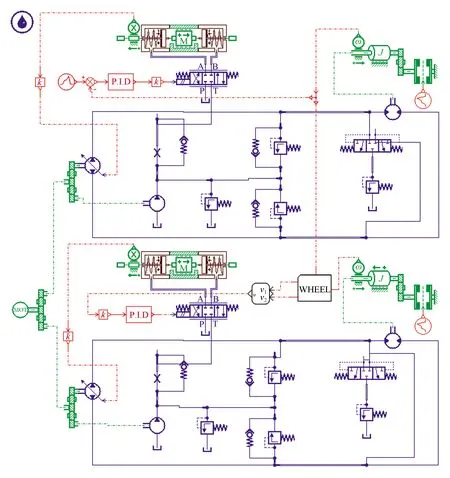
图7 履带支护车液压行走系统仿真模型Fig.7 Simulation model of crawler support vehicle
4.2 仿真分析
在局域栅格化场景中,履带支护车首先在常规地质路面行驶,外侧履带速度预期值设为 1 m/s, 4 s后外侧履带经过重黏土路段,3 s后外侧履带经过砂壤土路段。行进过程中履带支护车内侧履带进行泵控马达调速并保持直线导航行驶。模糊PID与传统PID调控的履带转速响应曲线如图8所示,调节时间较相近,但超调量较小,履带转速调节过程呈稳定势态。履带支护车的质心速度、转向角速度以及航向角变化曲线如图9和图10所示,模糊PID使其车体的平稳性能有了较大提升。由图10可知,从初始值为8°的航向角行进中,模糊PID的车体航向角最大偏差较传统PID减少了81.36%。
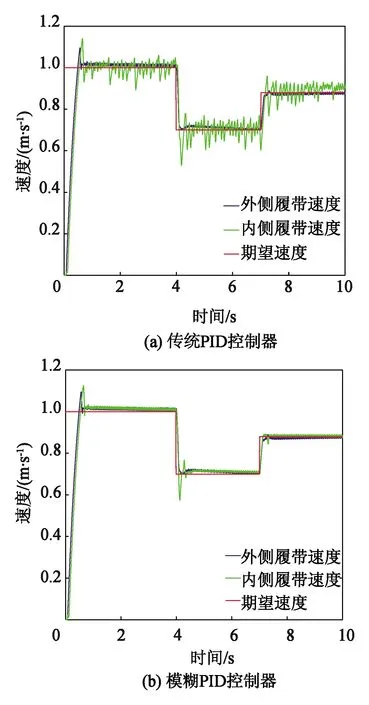
图8 不同控制器下的履带转速响应曲线Fig.8 Speed response curves with different controllers
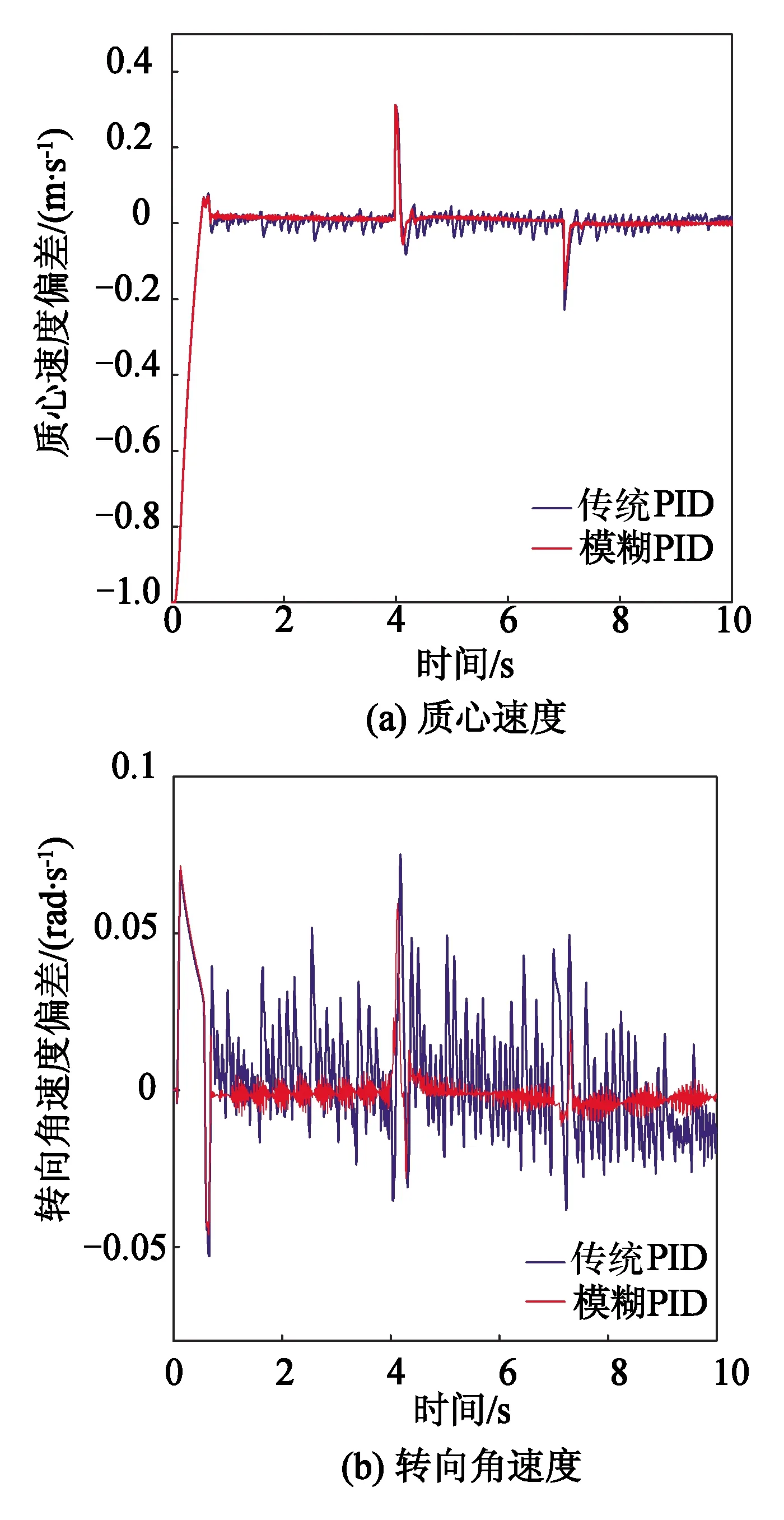
图9 速度变化曲线Fig.9 Curves of velocity
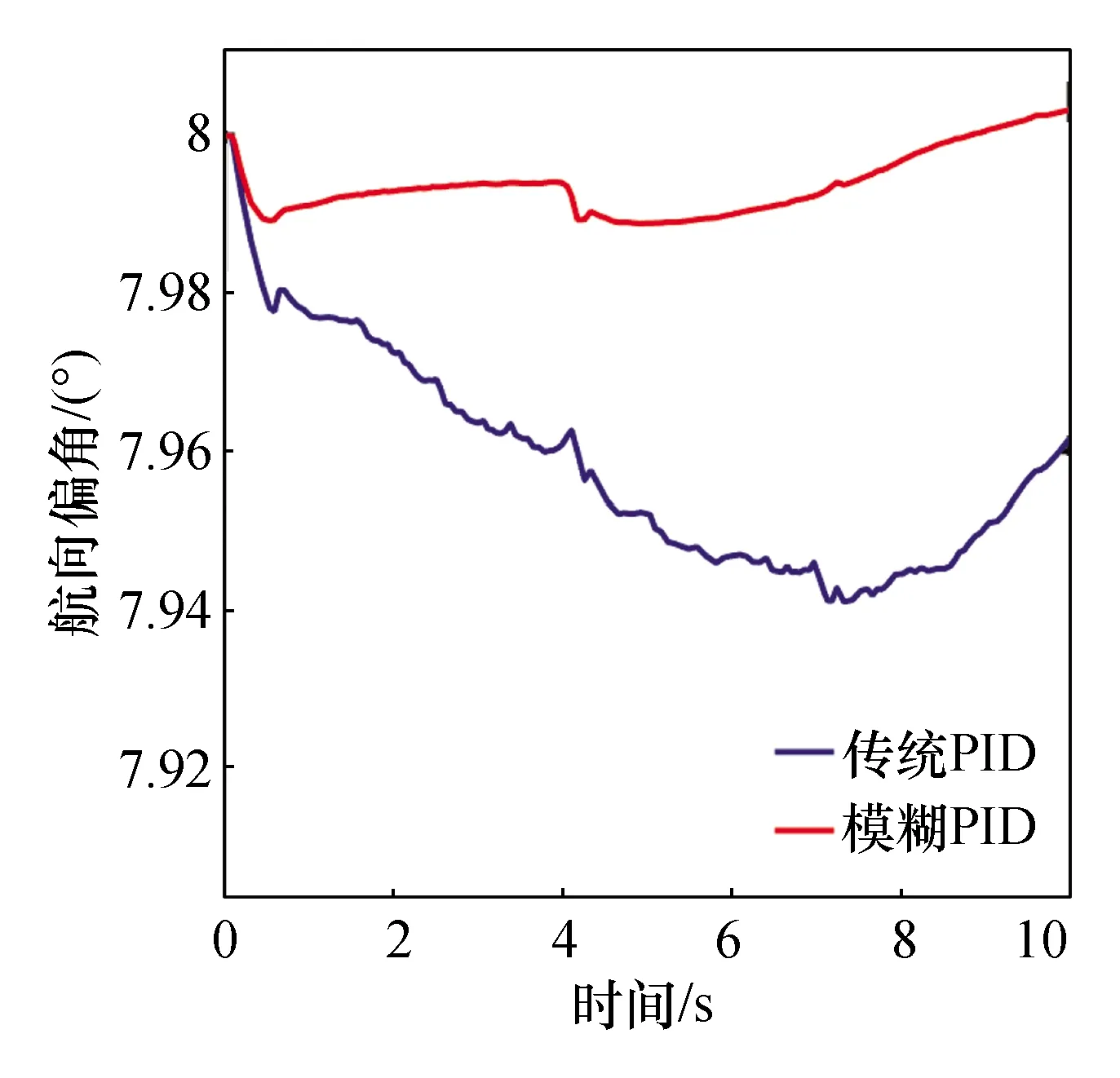
图10 航向角变化曲线Fig.10 Curves of course deviation
行进过程中履带支护车内侧履带进行泵控马达调速并完成转向导航行驶。模糊PID与传统PID调控的履带转速响应曲线如图11所示,模糊PID控制履带转速调节时间相比传统PID控制减少约0.62 s,超调量减少约16.75%,且转速调控过程更为平稳缓和。履带支护车的质心速度、转向角速度以及航向角变化曲线如图12和图13所示,传统PID控制下车体的质心速度偏差调节时间相比模糊PID增加约0.73 s,超调量增加约75.60%,由此履带支护车可能会在自主导航时出现振颤现象。当在转向角速度调节时,模糊PID偏差调节时间相比PID控制明显缩短,但超调量增加约15.33%。由图13可知,航向角偏差在模糊PID控制下的收敛性更加稳定,验证了栅格化场景内自主导航方法的可靠性。
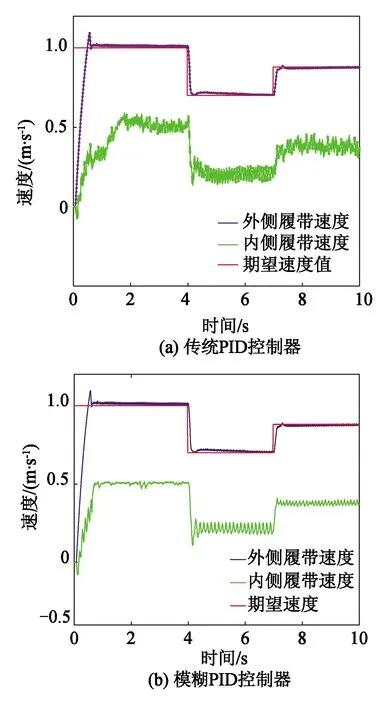
图11 不同控制器下的履带转速响应曲线Fig.11 Speed response curves with different controllers
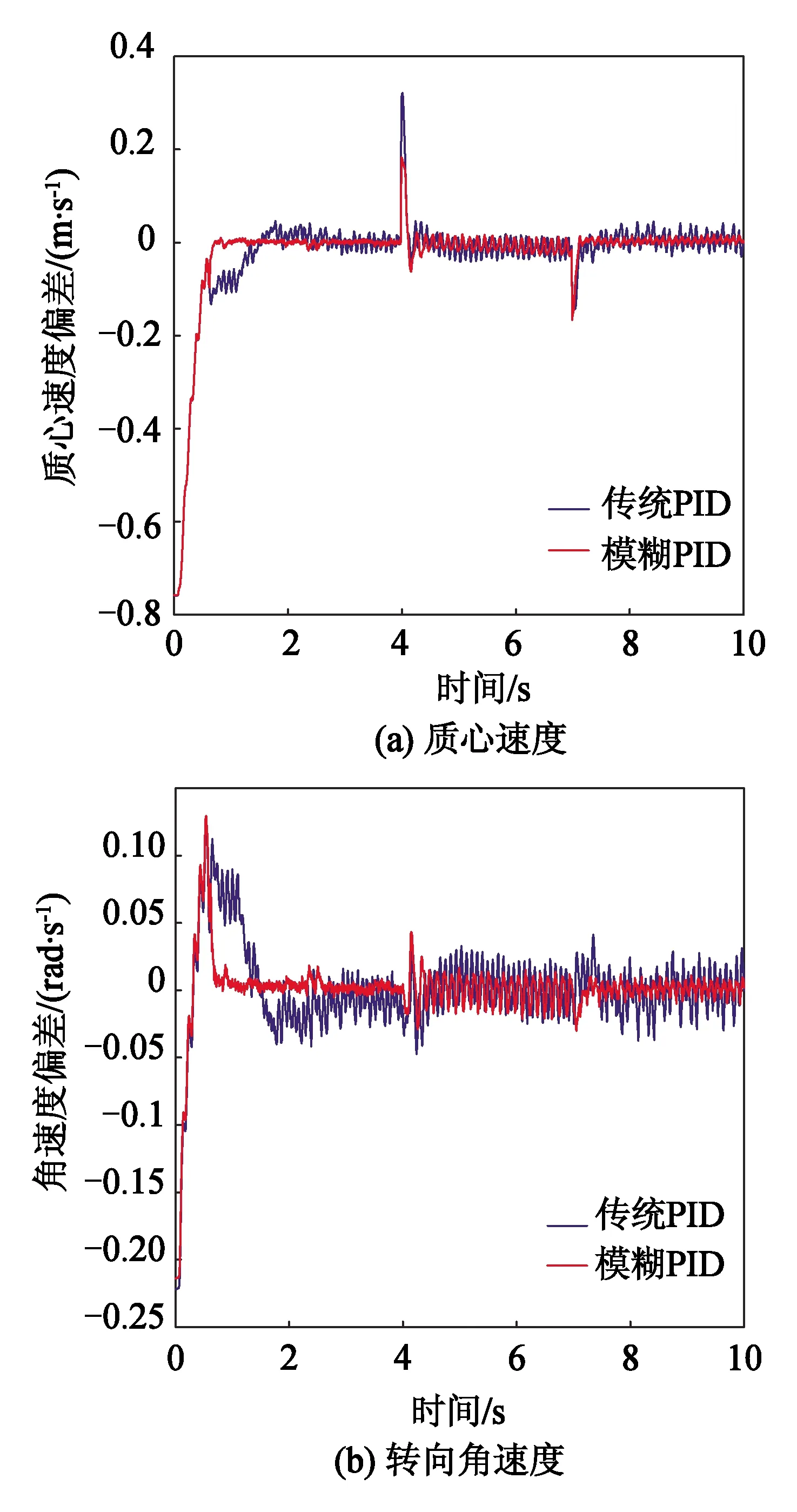
图12 速度偏差曲线Fig.12 Curves of velocity deviation
5 结 论
(1) 提出了一种综掘巷道自移式超前支护装备并阐述了其工艺原理。基于巷道实际工况环境,进行了受限巷道空间内的栅格化场景建模,提出了航向参考影响度指标来衡量巷道底板中非常规路况对于履带支护车驱动的影响能力,建立了适用于履带支护车自主导航控制方法的场景模型。
(2) 基于履带支护车的运动特性,构建了其在栅格化场景中的自主导航运动模型,并完成了履带支护车液压行走系统的数学建模,验证了该系统稳定性,设计了模糊PID控制器来满足系统的动态航向角纠偏精度需求。
(3) 履带支护车自主导航控制方法可以在受限巷道空间内栅格化场景中有较为良好的航向角纠偏精度,且在煤巷底板的不同地质条件下仍具有良好的控制品质与平稳性能。
