精设实验巧积累 发展思维提素养

钱燕

【摘要】《义务教育数学课程标准（2011年版）》明确指出，设计必要的数学活动，让学生通过观察、实验、猜测、推理、交流、反思等过程，感悟知识的形成和应用。可见，数学实验已经被认为是帮助学生积累“基本思想和基本活动经验”的有效途径。要让学生经历数学学习的全过程，启发学生在“做”中体验数学，在“思”中感悟数学，领会数学基本思想，积累数学活动经验，提升学科素养。

【关键词】数学实验   活动经验   思维

《义务教育数学课程标准（2011版）》（以下简称《课程标准》）中指出，学生的数学学习内容应该是现实的、有意义的、富有挑战性的，这些内容有利于学生进行观察、实验、猜测、验证、推理与交流等数学活动。同时强调，学生应该有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。可见，数学实验已经被认为是帮助学生积累“基本思想和基本活动经验”的有效途径。数学课堂应重视过程的教学，启发学生在“做”中体验数学，在“思”中感悟数学，发展数学思维，领会基本思想，积累活动经验，提升学科素养。在区名师送教活动中，笔者执教了苏教版六年级下册数学实验手册“包装箱的秘密”一课。笔者下面就结合这节课谈谈如何在教学中借助数学实验，在实验操作与思维生长的融合中积累数学活动经验的一些思考与体会。

一、创设情境，“趣”中激活已有经验

《课程标准》中强调：“数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上。”教师在教学中要从学生熟悉的现实情境和已有的知识经验出发，唤醒学生的已有认知经验，促进知识建构与经验迁移，为灵活运用已有数学活动经验和积累新的数学活动经验做铺垫。因此，教师要精心创设生活情境，激发学生学习数学的求知欲与好奇心，让学生自觉参与到数学活动中来，从而亲近数学。

笔者在本节课的导入环节创设了学生熟悉的“超市购物”生活情境，并提问：你觉得商家在设计包装箱时会考虑哪些因素？学生有的认为“会考虑包装盒的美观”，有的提到“要注意节省材料”……教师相机追问：“怎么包装最节省材料实际上就是数学上的什么问题？”自然而然引出本节课需要研究的内容：怎样包装表面积最小？设疑—追问—揭题，有效激发了学生的探究欲望，水到渠成地引入新知。

二、实验操作，“动”中积累实践经验

弗赖登塔尔说过，学数学的最好方法就是做数学。学生在外显的行为操作中可以获得来自感官、知觉的直接经验，数学实验正是通过做数学的探究学习活动，引导学生运用有关工具，在数学思维的积极参与下获得一些重要的发现，形成一些有价值的体验。在课堂上，教师应组织学生积极开展有效的探究活动，使其思维和想象处于活跃状态，获得深刻的体验，积累丰富的经验，从而促进其在知识、能力、情感态度上均得到发展，享受学习数学的乐趣。

【片段一】初探拼法，操作引发思考

研究复杂的问题，往往从简单开始。学生一致选择从研究棱长1厘米的小正方体开始。在之前的学习中，学生对两个小正方体拼成大长方体后表面积变小，减少了2个重叠的面是有感性认知的。教师基于学生的这种已有认知经验，抛出问题：用12个棱长1厘米的小正方体拼成大长方体，看看一共有多少种不同的拼法？”

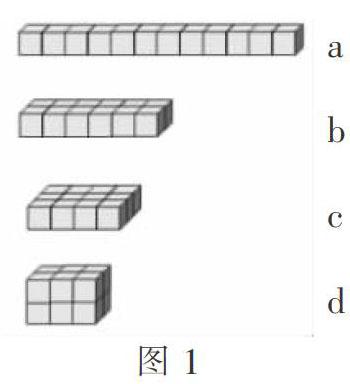
学生同桌两人合作，一人拼一人记录，交流反馈（见图1）：

师：哪种拼法的表面积最小？能结合图说一说你是怎么想的吗？

生：重叠的面越多，剩下的面积就越小，拼法a每个正方体只减少了1～2个面，而拼法d每个正方体减少了3～4個面。

教师引导学生借助表格进行整理后指出：拼法a、b、c，它们的高都是1厘米，拼法d高是2厘米，今后列举时，就可以从高1厘米、2厘米这样有序列举，既不重复，也不遗漏。

分组计算四种不同拼法得到的长方体表面积后，学生通过观察表中数据发现：体积不变的情况下，设计成长3厘米、宽2厘米、高2厘米的长方体最省材料。

思考：小学六年级学生是直观形象思维向抽象逻辑思维的过渡期，这个时期的儿童仍不能脱离直观形象思维。所以，此环节主要是让学生在用12个小正方体拼一拼的直观形象中，深切感受到：体积不变的长方体，小正方体重叠的面越多，拼成的长方体的表面积就越小。同时，也渗透了有序列举的方法。通过数学实验将操作和思考完美结合，思考引发操作，操作深化思考。学生基于对问题的思考进行操作，又在操作中修正和完善认知，从而加深对数学知识的理解，为后续的学习做好铺垫。

三、自主探究，“思”中总结活动经验

苏霍姆林斯基说，在人的心灵深处，都有一种根深蒂固的需要，就是希望自己是一个发现者、探索者。儿童更是这样，他们对自己感兴趣的事物产生疑问时，自主探索的欲望十分强烈。教师要创造自主探究的氛围，引导学生积极地进行观察、实验、猜想、推理、研讨等活动，自主地去发现数学、理解数学、创造数学。

【片段二】深入探究，产生思维碰撞

探究24个小正方体的包装问题。学生借助研究单有序列举出为24个棱长1厘米的小正方体设计包装盒的所有方法（见图2）。

为24个棱长1厘米小正方体设计包装盒，有几种方法？怎样设计表面积最小？学生发现重叠的面越多，拼成的长方体表面积越小。

师：大家对正方体的包装有点感觉了吧，其实生活中的大多数物体都是长方体的，如何进行长方体的包装呢？咱们继续来研究。

（出示一个长5厘米、宽3厘米、高2厘米的长方体）

师：两个完全相同的长方体拼在一起有几种拼法？（指名学生说，课件相机演示）

师：哪种拼法表面积最小？为什么？（见图3）

学生通过观察、比较、讨论后发现，重叠的面积

越大，拼成的长方体表面积越小。

思考：基于小学六年级学生的认知特点，由12个小正方体拼图形的经验迁移到24个小正方体的经验，学生不用拼，根据“重叠的面越多，拼成的长方体表面积越小这一经验”，就能很快得出哪种拼法表面积最小，大大节省了时间。接着去研究长方体的包装，学生的经验已经很丰富了，能够自觉地运用之前发现的规律解决新的问题，可见其数学思维及学科素养在正向迁移中得到了有效提升。

四、反思悟理，“静”中提升思维经验

数学的抽象性和思维的严谨性特征，与小学生以具体形象思维为主的思维特点形成了小学数学教学的矛盾。所以教师不能只停留在让学生通过动手操作解决问题上，必须对学生的活动经验进行适当的转化和提升，引导学生把抽象的数学知识与直观的形象有机结合，这也是实验教学的关键环节。实验积累的活动经验因思维发生质变，转化为一种静态的反思成果，让学生在学中思、思中悟、悟中得，思维水平真正得到提升。

【片段三】对比反思，促进思维提升

对比数据，发现规律。

师：观察表面积最小的情况，你又有什么新的发现？

师（小结）：若干个完全相同的小正方体或小长方体拼成大长方体，当长、宽、高越接近时，拼成的长方体的表面积越小。这是我们今天这节课所发现的规律。

运用规律，总结提升。

师：通过研究，我们知道要想拼成的长方体表面积最小，它们的长、宽、高要最接近。刚才，我们知道这两个长方体这样拼，表面积最小，长、宽、高是最接近的。

如果再来2个，要使拼成的长方体表面积最小，那长、宽、高分别是多少呢？

再来4个，共8个拼，没有图，只看数据，能知道长宽、高是多少时，表面积最小？

师（小结）：刚才在2个拼、4个拼、8个拼时，同学们根据数据，运用发现的规律一下子就找到了表面积最小的方法。

思考：此环节的设计，教师在带领学生逐个观察示意图的过程中，引导学生逐步发现每次把最大的两个面重叠，就会使长、宽、高中最小的数扩大到原来的2倍。以此类推，不拼、不算，只要根据长、宽、高这三个数据的大小就能类推出下次的摆法，从而得到更大长方体的相关数据。在这一层次的教学中，学生能够完全摆脱直观的束缚，仅仅借助数据就能推出最优的摆法，思维得到了質的提升。教师在教学中，通过提问、总结等多种途径培养了学生数学思维的条理性和逻辑性。

五、实践运用，“说”中内化拓展提升

《课程标准》指出：“人人都能获得良好的数学教育。”“不同的人在数学上得到不同的发展。”也就是说，学习数学应该满足学生未来生活的需要，引导学生在自己熟悉的生活背景中去发现数学、掌握数学、运用数学，让学生感受到数学学习的价值，体验到学习数学与个人成长的关系，从而增强学好数学的信心，学会用数学的眼光去观察事物，应用数学知识去解决实际生活中的问题。

在本节课的最后，笔者出示了这样两幅图（如下图），让学生用数学的眼光去解释这种现象。这一环节的设计，很好地体现了数学来源于生活，又应用于生活的理念。

总之，积累数学活动经验不是一蹴而就的事，教师要从有利于促进学生主动建构的角度出发，巧用数学实验引导学生主动参与，充分经历探究知识的全过程，使课堂教学更具数学味，更能引发学生的深度思考，促进学生思维的全面提升。

【参考文献】

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2]沈重予，王林.小学数学内容分析与教学指导[M].南京：江苏凤凰教育出版社，2015.

[3]张兴华.儿童学习心理与小学数学教学[M].南京：江苏教育出版社，2011.