基于改进遗传算法的机械臂时间最优轨迹规划

曾关平 王直杰

摘  要：机械臂的时间最优轨迹规划是指机械臂的末端关节在从初始位置到给定位置过程中，所花时间最短的轨迹规划。文章以七自由度机械臂为研究对象，在用三次多项式规划出机械臂运动轨迹的前提下，拟采用改进遗传算法的方法，用浮点编码和设计适应度函数，生成满足约束条件的初始种群，然后不断迭代直到满足算法终止条件为止，对机械臂的运动轨迹进行时间上的优化，通过将机械臂在全局寻优的方法，找到时间最短的方案。

关键词：机械臂;轨迹规划;时间最优;改进遗传算法

中图分类号：TP242         文献标志码：A         文章编号：2095-2945（2020）22-0006-04

Abstract： The time-optimal trajectory planning of the robotic arm refers to the trajectory planning that takes the shortest time from the initial position of the robotic arm to the given position. In this paper， a seven-degree-of-freedom manipulator is taken as the research object. On the premise of using three cubic polynomials to plan the trajectory of the manipulator， the method of improved genetic algorithm is used to generate the initial population that meets the constraints using floating-point coding and designing the fitness function Then， iterate continuously until the termination condition of the algorithm is satisfied， and optimize the time of the trajectory of the manipulator. By searching the manipulator in the global optimization method， the solution with the shortest time is found.

Keywords： manipulator; trajectory planning; time-optimal; improved genetic algorithm

引言

近年来，随着机器人技术的快速发展，针对机器人展开了各项技术研究。其中，针对机械臂轨迹规划的研究主要从关节空间轨迹规划和笛卡尔空间轨迹规划两种方面进行展开，而无论采用哪种规划方法所规划出来的轨迹，不管是从时间还是能耗以及关节冲击上都不是最优的，因此这就需要我们对规划好的轨迹进行优化找出一条最优的轨迹。随着企业对于生产效率要求的普遍提高，这就要求机械臂沿着规划的轨迹运行的同时还要求其运行的轨迹平滑连续。

为了更充分地利用机械臂动力性能，需要在保证机械臂约束的前提下对机械臂的运动轨迹进行优化。就目前来看，机器人适用的场合不同所优化目标也不尽相同，大致分为：运行时间优化、耗能优化和减冲击优化这三种[1]，本文主要针对时间优化展开研究。韦素云，徐敏使用双臂的机器人作为执行机构，将神经网络算法应用到了机械臂解耦问题上，取得了良好的效果，很好的避免了复杂轨迹优化收敛速度较慢及局部收敛的问题[2]。宫孟孟等人也是用神经网络的方法，来识别障碍物来进行避障，同时也能够判断设计出来的运动路线是否会与障碍物发生碰撞，在一定程度上可以提高计算速率[3]。文献[4]采用改进的蚁群算法和模糊PID控制算法对时间进行优化，很好地保证了时间以及冲击最优。本文采用改进遗传算法，对机械臂通过固定路径点进行时间最优的轨迹规划。

1 三次多项式插值规划轨迹

由于机械臂轨迹规划中，需要在轨迹中插入许多中间点，我们可以把相邻的每三个点都看作是轨迹的起始点、中间点和终止点，那么，每段軌迹的终止点的一二阶导数就是下一段起始点的一二阶导数，限制在于每个被当成是起始点或终止点的中间点的速度必须是连续的，而整段轨迹的起始点和中间点的速度均为0。设？兹0是关节的初始角度值，？兹f是终止点的关节角度值。三次多项式函数表达式为？兹（t）=a0+a1t+a2t2+a3t3。

在起始和终止点处的位移约束条件为：

关节速度约束条件为：

联立（1）和（2）：

2 改进遗传算法

2.1 浮点编码法

在机械臂的关节轨迹优化过程中，很多论文都采用的是传统的二进制编码方法，这种方法的好处在于直接简便，但其缺陷也很明显。例如，线性函数在离散化的过程中会产生误差;编码方法也对二进制编码优化的准确度有很大影响。为了解决这些问题，选择了浮点编码方法，作为一个时间间隔变量，以直接验证该变量与浮点的匹配性，在一定程度上减少了算法的计算量，从而加强了算法收敛的速度。

2.2 适应度函数设计

在适应度函数的设计方面，为了防止算法出现较大的误差，因此采用罚函数法，对约束条件中的个体进行筛选，满足要求的种群后代不会受到惩罚，而不满足的后代则将会施加惩罚。根据算法迭代中种群的基因变化情况，调整罚函数的约束，使得误差趋于最小化，算法更加精确。适应度函数为：

其中，？滓为惩罚系数，取值0.1;P（t）为惩罚项。当关节的各个参数值都满足公式中的约束条件时，这时P（t）的值不发生变化，相反，如果关节的参数超过了设定好的区域，这时需要加大惩罚来使得参数满足约束条件要求。这时，建立的单独适应度函数为：

在种群不断进化筛选的过程中，种群中的优良个体数量也会越来越多，所以，这时就需要调整独立的适应度函数，使种群能够在这些个体中挑选出最接近最优解的个体。重新调整适应度函数：

对上式的适应度重新标定为：

其中，F（t）为调整过后的适应度的取值;Fit（t）min为初始的适应度函数值的最小值;Fit（t）max为初始的适应度函数的最大值;？啄为常系数，取值在0～1之间。

2.3 遗传算子的改进

（1）选择

轮盘赌选择是目前使用的最多的选择算法，很多的遗传算法也是如此，但是这种方法在收敛方面不能满足本文要求。在种群遗传过程中，会不断产生新个体，这样会导致其中的一些本就比较优秀的成员因为遗传而导致基因发生改变，所以，本文在种群中选择一些相对比较满足要求的个体，不再进行交叉，而是直接将基因传到下一代，即精英保留策略。

（2）交叉和变异

遗传算法的交叉概率和遗传概率应当随着适应度值做出相应的变化，因此对交叉和变异所取概率进行改进，利用正弦函数对算法交叉算子和变异算子进行改进，使算法交叉概率和变异概率随着个体适应度值自动调整并做非线性变化。

改进后的交叉概率Pc和变异概率Pm为：

在这种情况下，各个系数的取值与自适应遗传算法的系数相差不大。与改进前的遗传算法相比，运用了正弦曲线的方法，使得交叉概率和算法变化概率不再是常数，而是跟随个体适应性的正反变化。当个体的适应度比较不符合种群进化方向时，提高个体的变异概率;当个体的适应度太高导致种群过早收敛时，降低个体的变异概率。因此，算法根据实际情况能够对变异概率做出相应的调整，从而避免算法陷入局部最优，并确保算法能够在一定时间内完成收敛。

交叉算子的表达式为：

其中，？琢是区间[0，1]上的任意数值。

浮点编码法交叉算子为：

2.4 改进的算法流程

（1）定义种群遗传过程中的各项参数，同时进行初始化：Pm和Pc分别代表遗传算法的变异概率和交叉概率;种群的数量N;迭代的次数g;机械臂运动的时间段n。

（2）定义算法的约束条件。对算法需要解决的问题，即关节运动时间总和，施加关节的角速度和角加速度约束，以免算法得出的解超出了关节的限制。

（3）初始种群的生成。用随机数法生成满足条件的初始种群N。

（4）对生成的种群进行交叉和变异，根据基因的交换结合形成新的个体，其中概率的变化依据改进后的公式来选择。

（5）根据优胜劣汰的进化法则，父代通过交叉变异后，将两代的个体结合，根据设定好的条件判断个体是否优良，筛选出优良个体，组成新的种群，然后进行下一次遗传。

（6）每一次遗传后对种群进行判断。如果满足结束条件，则停止迭代过程，不满足则继续（4）的操作。

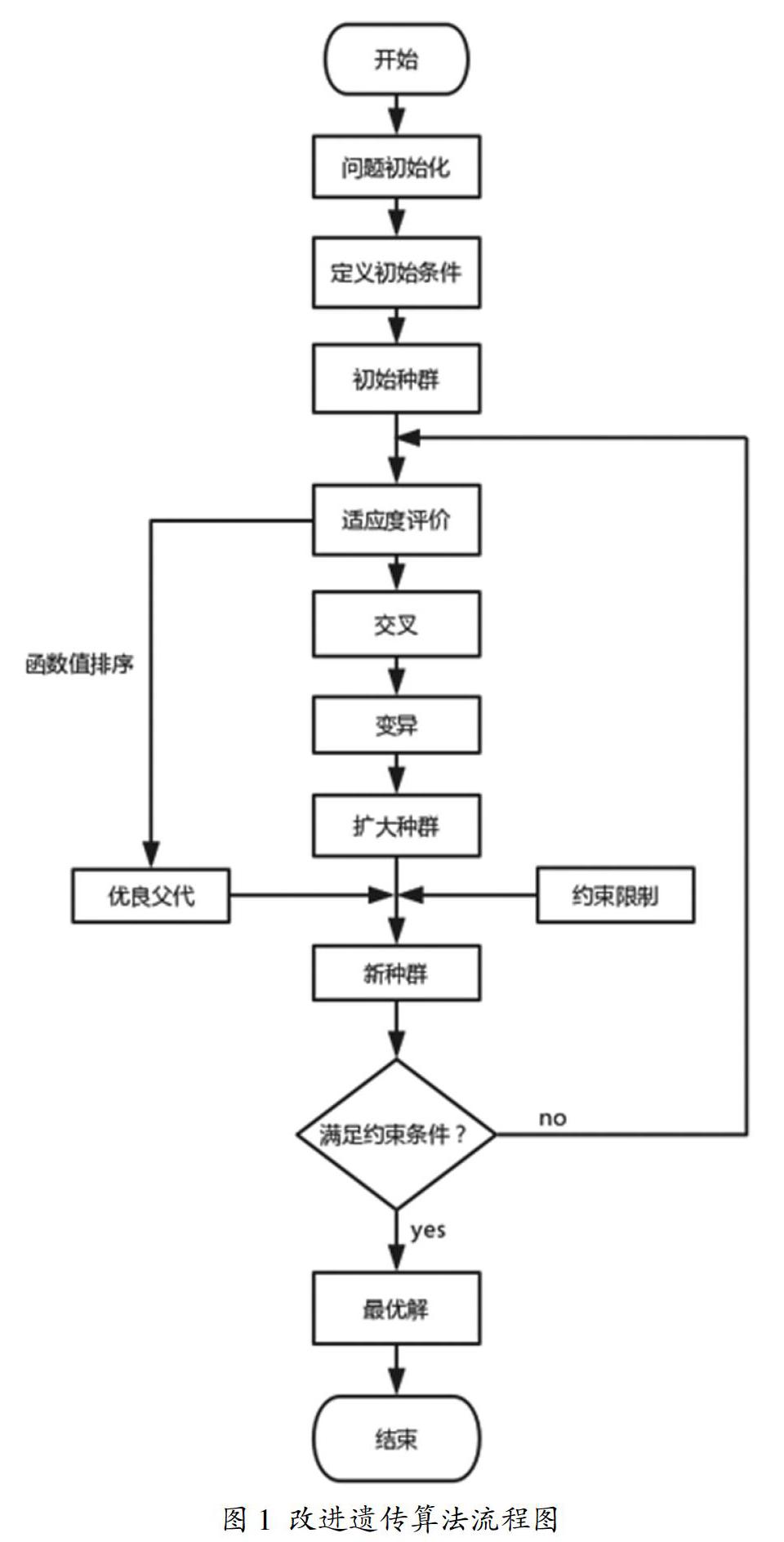
遗传算法的流程如图1所示：

标准遗传算法和改进遗传算法迭代收敛速度比较（见图2、3）。

从图2和图3可以看出，改进后的算法在30代左右就已经开始收敛，而传统的方法此时还处于变化过程，直到45代左右才开始收敛过程。改进遗传算法的收敛速度比标准的遗传算法在收敛速度上更加快速，证明了改进后，算法在时间效率上节省了很多时间。从这两个图也能看出，在时间上，改进后的算法明显缩短了优化的时间，大约节省了1.2s。

从表1中可以看出，对于每一段关节间的轨迹，算法都实现了优化过程，由于每段轨迹的时间都设置成了4s，所以可以很明显地看到，优化后之间基本控制在2s到4s之间，优化后的效果可见一斑。将所有的分段轨迹结合后，得到的总时间也可以看出，原本的轨迹需要20s的时间才能到达，优化后最短只需要13.2s，优化了将近33%。

3 结束语

本文采用七自由度机械臂为研究对象，根据运动学约束采用了三次多项式的插值算法规划路径，然后采用改进遗传算法对轨迹进行时间上的优化，最终规划出了每个关节的轨迹，且在保证关节的位移，速度，加速度曲线平滑的条件下缩短了机械臂的运行时间。

参考文献：

[1]居鹤华，付荣.基于GA时间最优机械臂轨规划算法[J].控制工程，2012，19（03）：472-477.

[2]韦素云，徐敏.双臂机器人神经网络解耦与路径规划算法研究[J].机械设计与制造，2017（08）：245-248.

[3]宫孟孟.基于神经网络的移动机器人路径规划方法研究[D].哈尔滨工业大学，2017.

[4]王文杰，秦现生.基于jerk最优的机械臂轨迹规划[J].机械传动，201746（3）：93-125.

[5]牛永康.六自由度串聯机器人轨迹规划时间最优研究[D].长春工业大学，2013.

[6]Yang F， Ding L， Yang C， Yuan X. An algorithm for simulating human arm movement considering the comfort level[J]. Simulation Modelling Practice & Theory， 2005， 13（5）：437-449.

[7]Shimizu M， Kakuya H， Yoon W K， Kitagaki K， Kosuge K. Analytical Inverse Kinematic Computation for 7-DOF Redundant Manipulators With Joint Limits and Its Application to Redundancy Resolution[J]. IEEE Transactions on Robotics， 2008， 24（5）：1131-1142.

[8]Sciavicco L， Siciliano B. Modeling and Control of Robot Manipulators[J]. Industrial Robot An International Journal， 1996， 21（1）：99-100.