泡沫金属在熔盐相变蓄热中的强化传热特性
2020-07-25陈岩叶宇轩杜文静
陈岩,叶宇轩,杜文静
(山东大学能源与动力工程学院,山东济南250061)
相变蓄热由于其储能密度大,熔化和凝固过程近似等温、易于控制等优势,广泛用于太阳能发电[1-3]、工业余热回收[4-6]、建筑节能等领域[7-9]。熔盐储能技术是将固态无机盐或混合无机盐加热融化,通过熔盐循环回路将存储的热量进行传递,实现熔盐的蓄热传热功能。与传统蓄热工质相比,熔盐具有传热性能好、使用温度范围广、蒸气压低、比热容大、高温黏度小、热稳定性高、价廉易得等特点,是一种优良的传热蓄热介质。相比于电化学储能,熔盐储能在可再生能源消纳、清洁能源取暖等方面,具有更多优势和更大应用潜力[10-13]。然而熔盐作为相变蓄热材料存在热导率低的缺点,导致了蓄热效率较低,限制了熔盐相变蓄热技术的发展。因此国内外学者为了提高熔盐相变材料的蓄热性能进行了大量研究。
美国橡树岭国家实验室对多种熔盐的理化特性以及其与结构材料的相容性进行了深入研究[14]。Tao 等[15]综述了添加高导热材料和多孔介质提高相变材料的导热性[16-18]、利用翅片管等结构设计提高换热面积[19-21]和采用梯级换热技术[22-24]三种方法来提高熔盐蓄热效率。Al-Abidi 等[25-26]构建了内外翅片三套管蓄热单元二维模型,利用Fluent软件进行数值模拟,考虑了热传导和自然对流,分析了轴向翅片数量、长度、厚度以及排列方式对相变材料完全熔化时间的影响,结果表明,最好的翅片布置相比与光管,完全熔化时间减少了34.7%。Zhao等[27-28]通过实验的方法,研究了在硝酸盐中加入多种金属泡沫、膨胀石墨对蓄热过程的影响,发现加入泡沫金属和膨胀石墨均能够提高熔盐的换热速率,且泡沫金属效果较好。李文强等[29]建立了金属泡沫内固液相变的两方程数学物理模型,数值模拟研究了石蜡在不同泡沫金属孔隙率下熔化过程内部速度场和温度场随时间的变化规律。杨佳霖等[30]构建了三层管肋式熔盐相变蓄热结构的物理模型,数值研究了相变界面随时间的变化以及自然对流对熔化过程的影响机制。
对于强化蓄热技术的研究主要采用单一的数值模拟或实验方法,当前研究中泡沫金属填充方法为网状覆盖式。本文为了降低泡沫金属对自然对流的抑制,提升蓄热速率,提出一种圆筒插入式填充方法,并研究其对于熔盐蓄热特性的影响。搭建了熔盐蓄热实验平台,同时结合数值模拟方法,对不同参数泡沫金属工况下熔盐蓄热性能及各位置温度的变化情况进行了讨论分析。相关研究为进一步强化熔盐的蓄热特性提供了一定的依据和参考。
1 实验研究
1.1 实验系统
图1、图2 为实验系统的实物图和示意图,主要包括熔盐蓄热容器、恒热流电加热器、Pt100 铂电阻测温元件以及无纸记录仪。蓄热容器材质为304不锈钢,高120mm,壁厚6mm。容器表面和顶部布置有15mm厚硅酸铝保温材料,以减少热量损失。容器内设置4个位于蓄热材料中心处的温度测点,如图3 所示,测点间距20mm。实验前对热电阻进行标定,其测温误差在±1℃以内。加热器加热功率为250W。实验使用的熔盐为三元硝酸盐,质量比为(40%NaNO3-40%KNO3-20%NaNO2),相关物性参数来自生产厂家,见表1。
1.2 实验结果

图1 实验系统实物
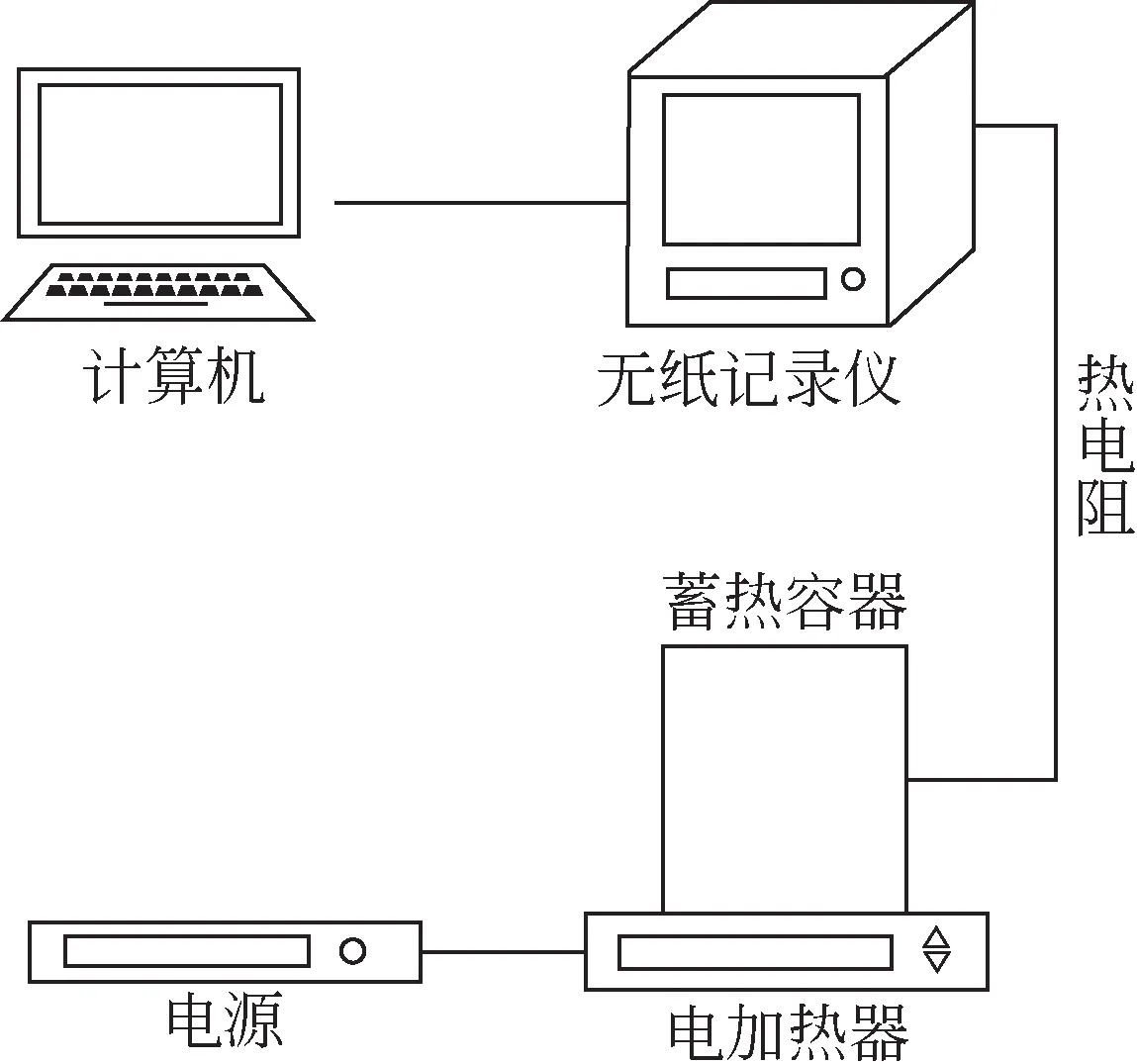
图2 实验系统
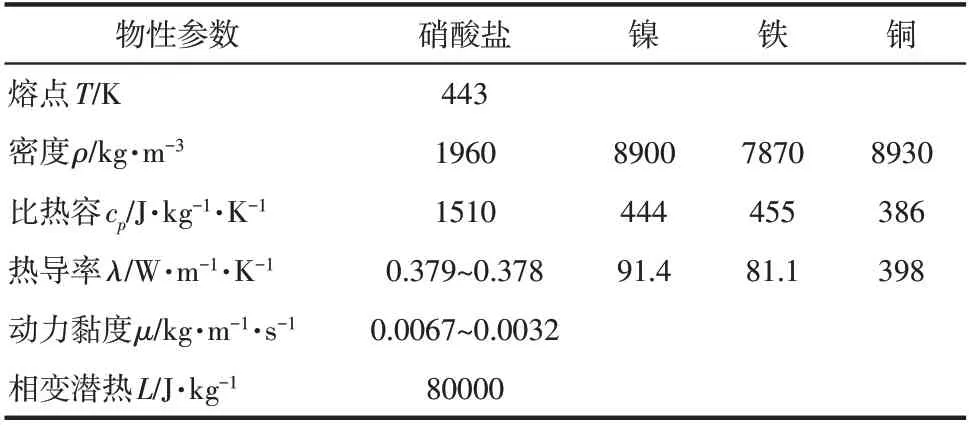
表1 材料热物性参数
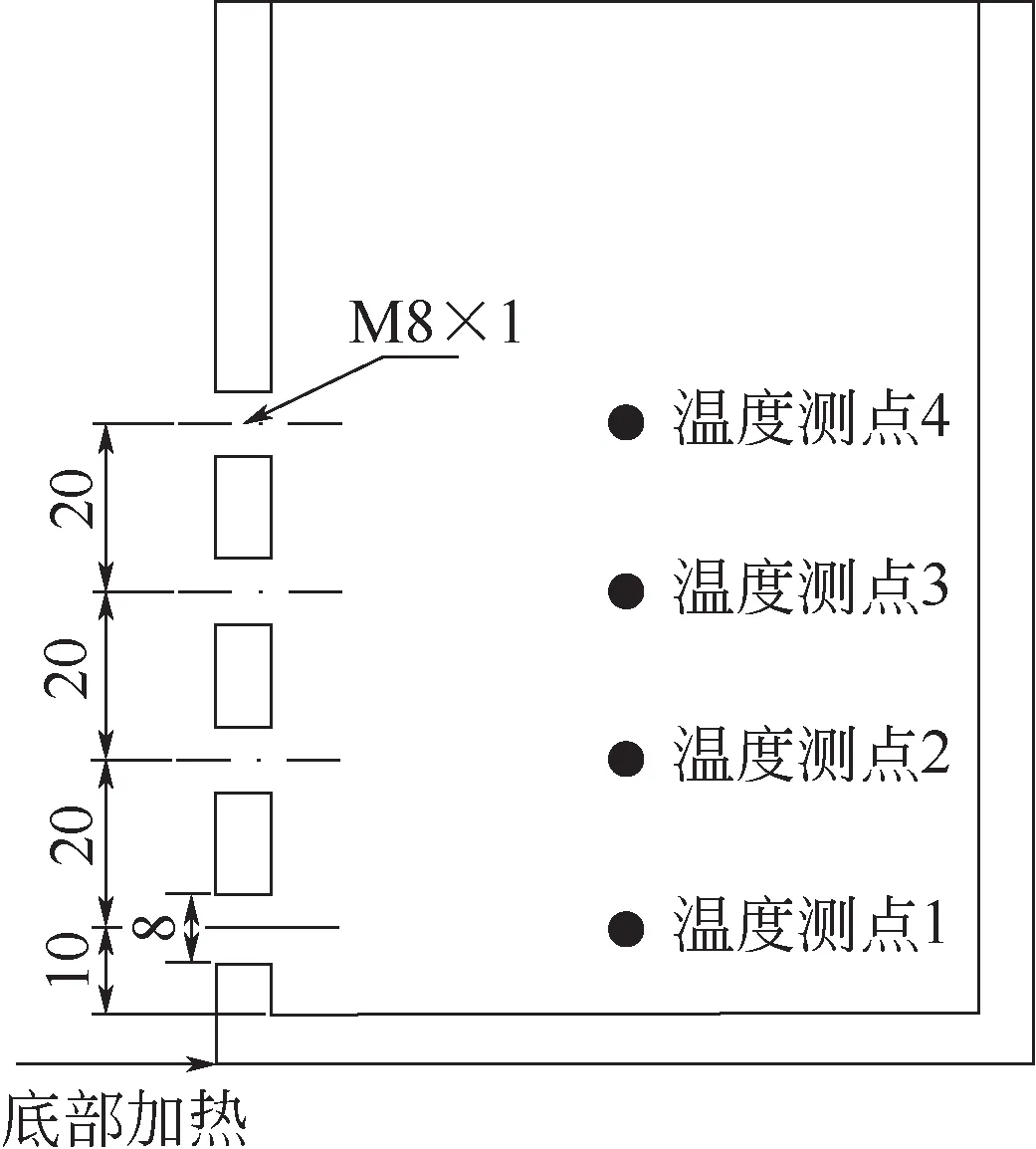
图3 蓄热容器温度测点分布(单位:mm)
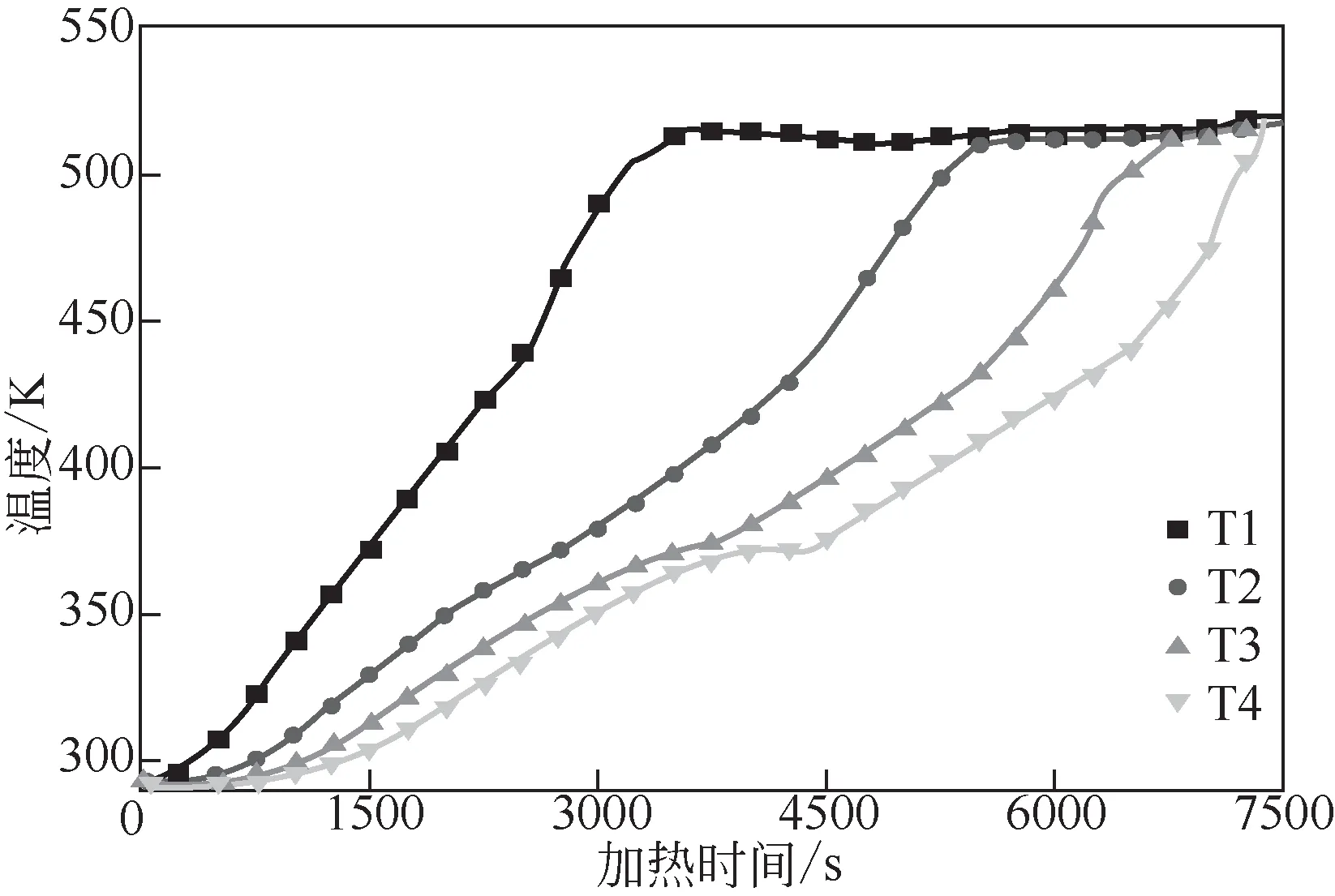
图4 蓄热过程熔盐温度变化曲线
实验过程中使用无纸记录仪收集温度测量数据,4个测点温度变化曲线如图4所示。由图可知,不同高度位置温度依次上升。起始阶段为固态导热,温度升高较快。当熔盐温度达到熔点时开始发生相变,T3、T4 两条曲线斜率明显减小,温度升高较慢。由于底部加热,容器底部温度升高快,导致T1、T2 两测点处相变过程在短时间内完成,无明显斜率减小现象。熔盐相变完成后,液态熔盐自然对流换热逐渐加强,温度升高速率开始增加,直到容器内外换热平衡,熔盐温度不再升高。
2 数值模拟
2.1 物理模型
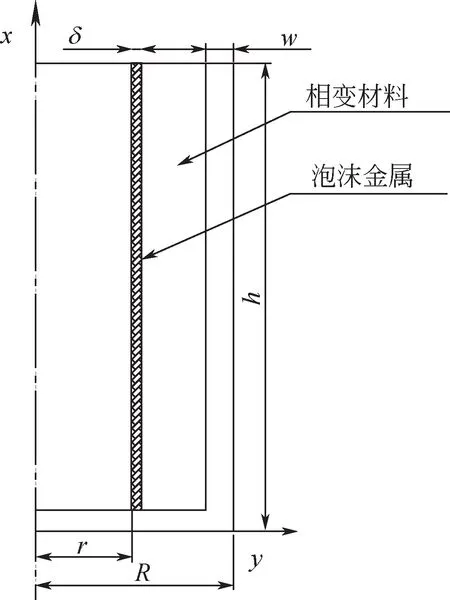
图5 物理模型

表2 物理模型结构参数
为了强化传热过程,减少熔盐蓄热时间,在蓄热容器中竖直布置了一圈泡沫镍,旨在利用泡沫金属热导率较高的优点,提高熔盐蓄热速率。图5为蓄热容器二维轴对称物理模型。蓄热容器及填充泡沫镍材料几何尺寸见表2,泡沫镍孔隙率ε为95%、90%、85%,孔密度为20PPI(即每英寸直线长度上孔平均数目)。
2.2 数学模型
在开展利用物理模型进行数值计算之前,进行如下假设。
(1)外壁面绝热,忽略热损失。
(2)相变材料具有各向同性,且均匀分布,其热导率、比热容、动力黏度在发生相变过程中随温度变化呈线性相关。熔盐物性与温度变化规律如下:T=423K,热导率λ=0.379W/(m·K),动力黏度μ=0.0067kg/(m·s);T=433K,热导率λ=0.378W/(m·K),动力黏度μ=0.0032kg/(m·s),比热容在一定温度范围内变化小,取cp=1510J/(kg·K)。
(3)泡沫金属物性参数不随温度变化。
(4)忽略相变材料在相变熔化过程中的体积膨胀。
相变过程使用Solidification/Melting 模型进行模拟,即将计算区域看作是一个多孔介质区域,多孔介质的孔隙率等价于液相分数。液相率β 的定义见式(1)。
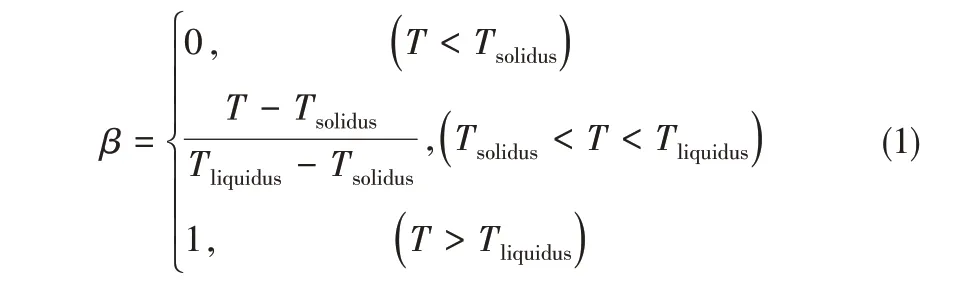
当β=0 时,相变材料为固态;当0<β<1 时,相变材料为固液混合状态;当β=1时,相变材料为液态。通过液相率可以表征整个计算区域固液相的分布特性。相变材料的焓值以式(2)、式(3)计算。
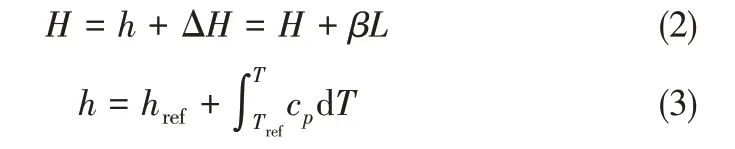
由于相变区域采用Boussinesq 近似,即忽略压强引起的密度变化,只考虑温度引起的密度变化,且密度随温度呈线性变化。熔化区内任意点的密度以式(4)计算。
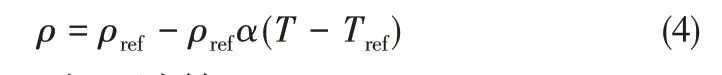
有效压力以式(5)计算。

轴向上的动量方程中压力梯度和重力项以式(6)计算。
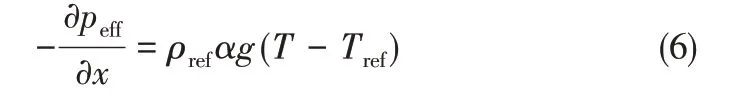
多孔相变区域模型
连续性方程见式(7)。
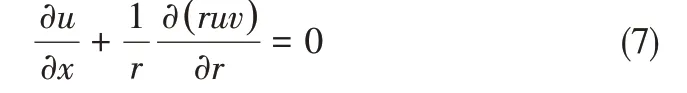
能量方程见式(8)、式(9)。
对于泡沫金属
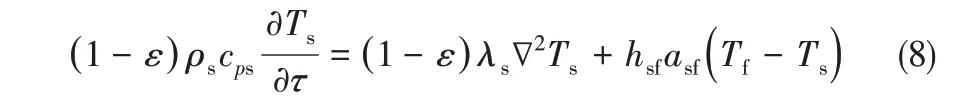
对于相变材料
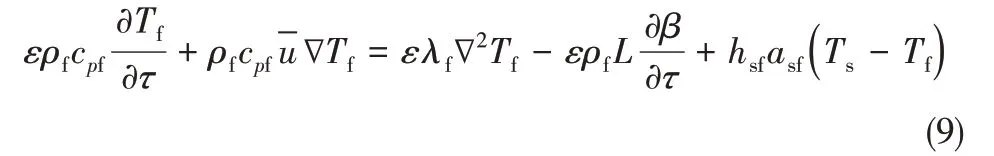
动量方程见式(10)~式(13)。
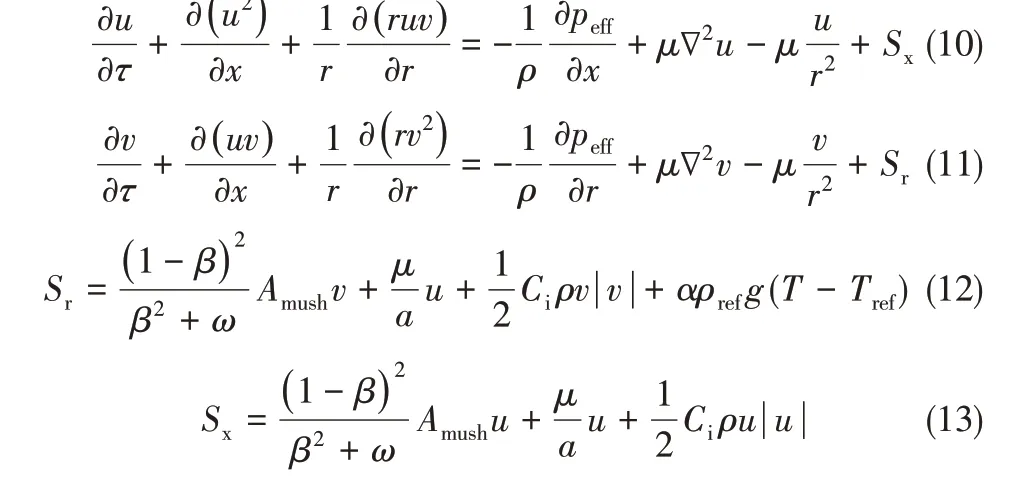
2.3 数值计算方法
蓄热容器在结构上具有对称性。因此,本文计算区域选择蓄热单元二维模型的右半部分,网格采用四边形网格。外壁面和上壁面定义为绝热边界,对于壁面与相变材料采用耦合的无滑移边界,相变材料和泡沫金属之间设置interface,容器底部定义为恒热流条件,热流密度为15000W/m2。求解器采用非耦合、隐式、二维轴对称求解方法;打开solidfication & melting 熔化凝固模型,传热、流动模型选用层流模型;考虑重力作用,采用Boussinesq模型考虑浮力驱动;采用SIMPLE 算法处理压力和速度场的耦合,选择二阶迎风差分算法处理动量方程,一阶迎风差分算法处理能量方程,采用PRESTO算法处理压力修正方程,松弛因子保持默认设置;以连续性和动量方程相对残差小于10-3作为收敛性判据,能量方程中变量的相对残差小于10-6;用PATCH面板设定固体区域与相变区域初始温度。
对网格数量进行无关性验证。验证了35292、46208、62160、71550、89712 五套网格数量,发现当数量达到71550时可以满足计算精度要求。由于本文所模拟为非稳态传热过程,故还需要进行时间步长独立性验证,确定计算时间步长取1s。
2.4 模型验证
为了验证本文数值模拟方法的可靠性和准确性,将相同工况下数值模拟结果与前文实验结果进行对比。测点T1 温度变化曲线对比结果如图6 所示,由于实验过程中会有一定热量损失,T1 测点温度实验数据会小于模拟数据。数值模拟结果与实验结果之间最大相对误差为13.8%,具有较好的一致性。因此,数值模型能够较好地预测蓄热特性。
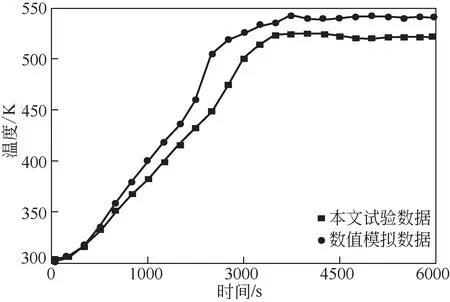
图6 模型验证(T1测点处熔盐温度随时间的变化)
3 数值模拟结果与讨论
3.1 泡沫镍填充位置不同时蓄热性能对比
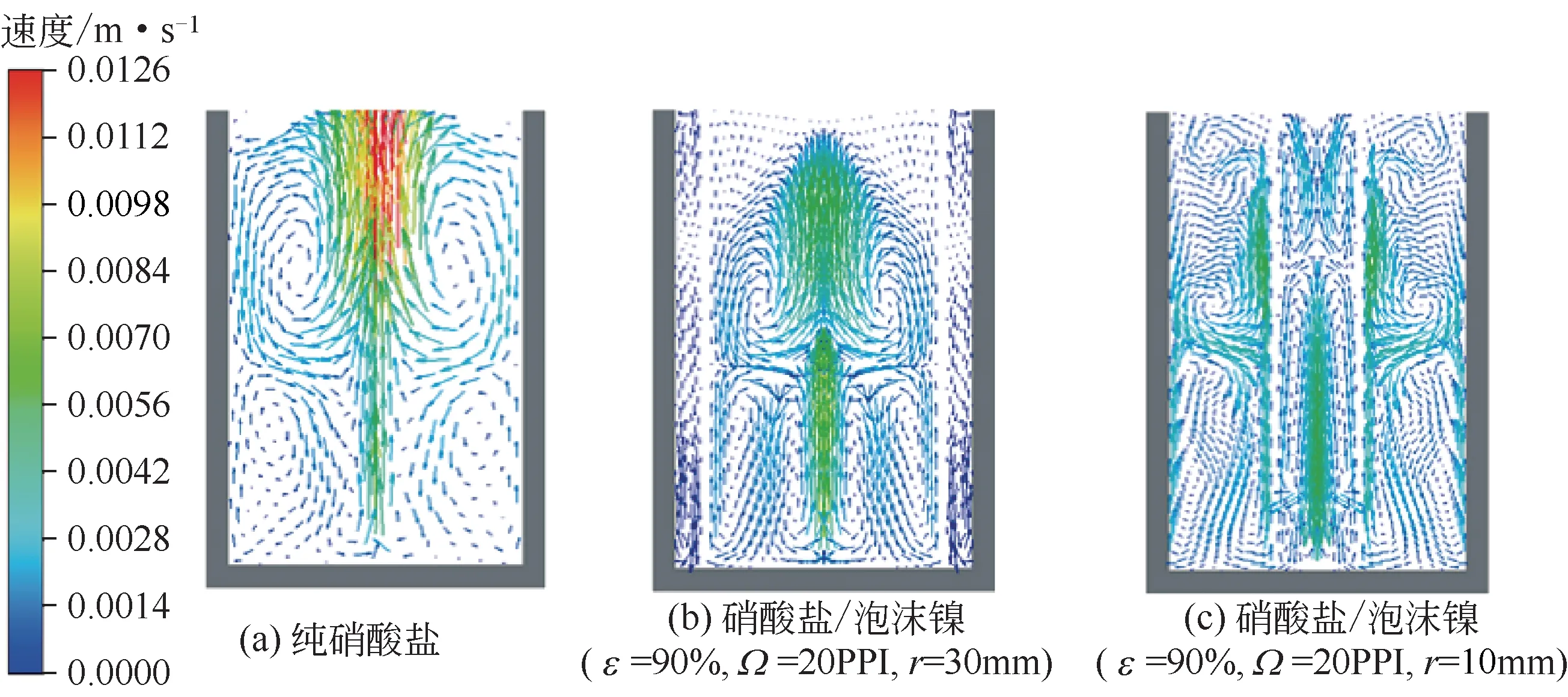
图7 4800s时熔盐速度分布
图7 是蓄热时间为4800s 时,纯硝酸盐和不同填充位置(r=10mm 和30mm)泡沫镍工况下速度矢量对比。由图可知,在加热纯硝酸盐过程中,自然对流主要集中在容器中心位置。由于温度梯度的影响,中心与壁面之间形成了4个发展完全的涡流。由于泡沫金属是一种多孔立体骨架结构,孔隙较小,该结构会阻碍液态熔盐的流动。填加泡沫镍后,泡沫金属支架抑制了中心处自然对流,泡沫镍布置越靠近中心位置,限制涡流的产生,中心处流动速度越小,对自然对流抑制作用越强;同时由图7(c)可以看到,泡沫镍布置靠近中心位置时,泡沫镍与壁面之间的自然对流相较于中心处自然对流更为剧烈。
图8 为3500s 后纯硝酸盐和不同填充位置泡沫镍工况下T1 与T3 测点之间温差ΔT 随时间变化曲线。当蓄热时间超过3500s,容器内自然对流换热占主导地位,对比泡沫镍不同填充位置工况结果发现,泡沫镍填充位置r 越小,T1 与T3 两测点处温差越大,泡沫金属对于熔盐自然对流的抑制作用越强,容器内熔盐换热效果越差。
3.2 填充不同泡沫金属时蓄热性能对比
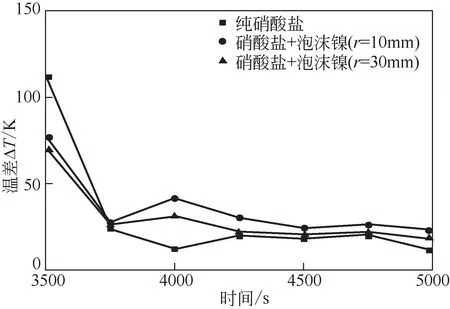
图8 3500s后纯硝酸盐与泡沫镍不同填加位置之间的热性能对比
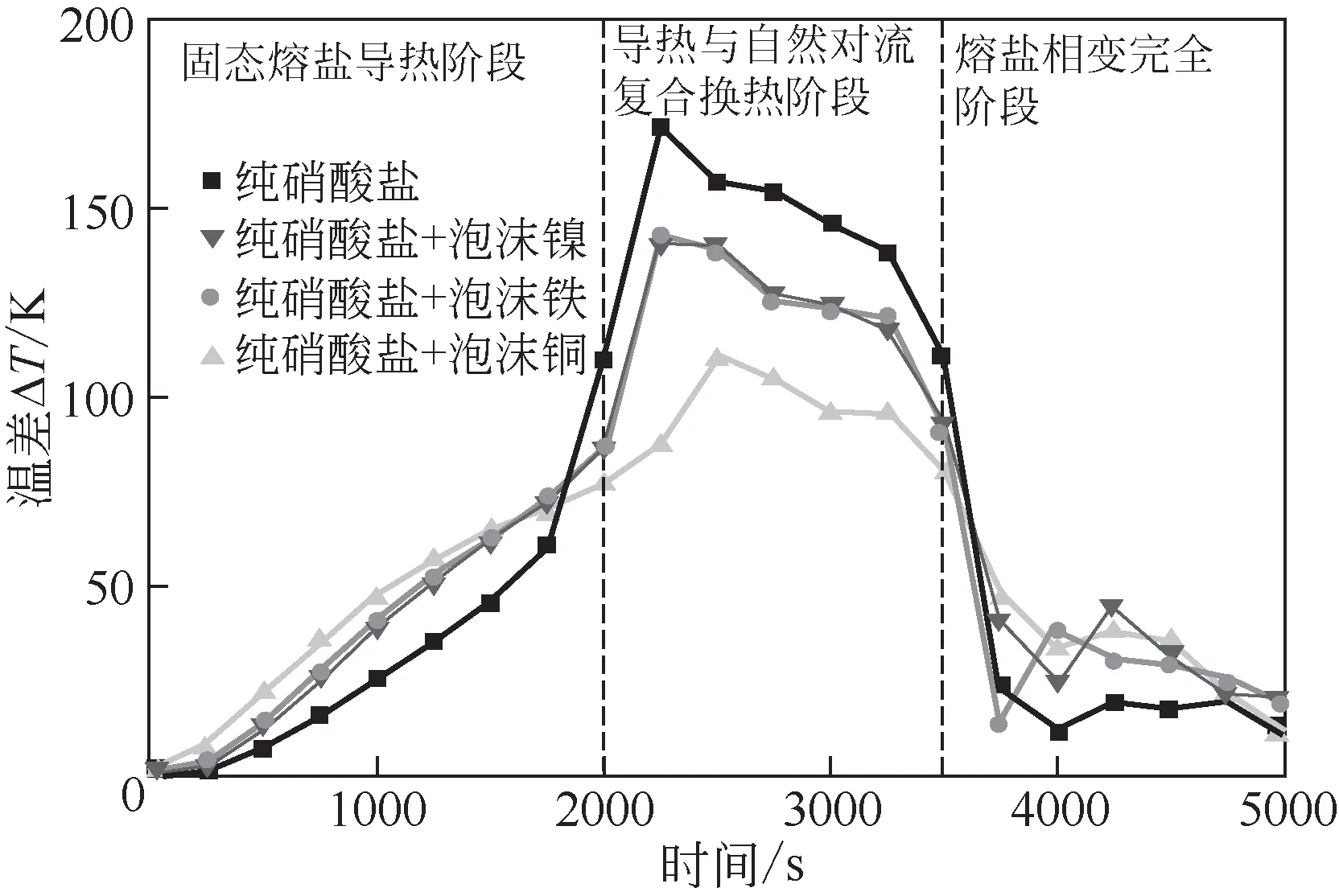
图9 纯硝酸盐与不同泡沫金属之间热性能对比
图9 为在填加孔隙率为90%,孔密度为20PPI泡沫镍、泡沫铁和泡沫铜工况下,T1 与T3 测点之间温差ΔT 随时间变化曲线,泡沫金属填充位置半径r=10mm。在固态熔盐导热阶段,纯硝酸盐ΔT最小,换热速率最高。三种泡沫金属中泡沫铜热导率大,导热阶段吸收较多热量,熔盐温度升高速率减慢,该工况下ΔT 最大。在导热与自然对流复合换热阶段,纯硝酸盐ΔT 最大,换热速率最低,其最大值为填加泡沫镍、泡沫铁ΔT的1.2倍和泡沫铜的1.6 倍。主要原因是泡沫金属支架热导率大,强化熔盐的导热,其中泡沫铜热导率最大,强化导热效果最好。最后熔盐基本熔化完全,泡沫金属的存在抑制了熔盐自然对流换热导致纯硝酸盐ΔT最小。
3.3 填充不同孔隙率泡沫镍蓄热性能对比
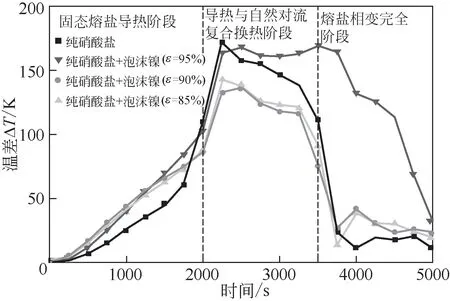
图10 纯硝酸盐与填加泡沫镍之间热性能对比
图10给出了填充不同孔隙率泡沫镍时T1与T3测点之间温差ΔT 随时间变化曲线,其中泡沫金属填充位置半径r=10mm。由图可知,整个蓄热过程分为3 个阶段。第1 阶段为0~2000s,即固态熔盐导热阶段,该时间段内纯硝酸盐ΔT 最小,表明在固态导热阶段纯硝酸盐的换热速率相较于填加泡沫金属较高。这是由于竖直布置泡沫镍支架热导率较大,部分热量直接被其吸收,导致熔盐温度上升减慢。同时该阶段泡沫镍孔隙率变化对换热速率无明显影响。第2 阶段为2000~3500s,此时部分熔盐发生相变,容器中换热方式转变为自然对流换热和导热两种,可以发现填充的泡沫金属孔隙率为90%、85%的泡沫镍可以显著提高换热速率,换热速率为纯硝酸盐的1.2 倍,填充的泡沫金属孔隙率为95%的泡沫镍时ΔT 较大。这是由于孔隙率较低时,泡沫镍支架紧密,有利于热量扩散。孔隙率为95%泡沫镍提高导热效果不明显,反而其存在会抑制自然对流换热,导致换热速率较差。第3阶段为3500~5000s,此时大部分熔盐相变完成,自然对流换热占主导地位,由于泡沫镍抑制自然对流,在该阶段纯硝酸盐的ΔT最小。
图11 为纯硝酸盐与填加泡沫镍两种工况下熔盐熔化过程液相率及温度对比云图,其中左侧为液相率云图,右侧为温度云图。与图7 结合可以发现,纯硝酸盐熔化过程中,容器壁面金属热导率高、中心处自然对流较为剧烈,两位置处熔盐熔化速度快,导致容器内熔盐温度梯度沿径向先减小后增大,温度分布均匀性较差,熔盐固液界面存在明显凹陷。
由于部分热量直接传递给壁面,因此存在一定的热损失。在竖直布置泡沫镍(ε=90%,Ω=20PPI)后,泡沫镍热导率高,同一时间点下其内部及附近处熔盐温度升高加快,蓄热过程熔盐温度分布均匀性较好。泡沫镍会抑制液态熔盐自然对流,自然对流导致的固液界面中心凸起较小,中心处熔盐熔化速度减慢。在4800s蓄热最后阶段,相对纯硝酸盐工况壁面温度较低,热量损失较小。
4 结论
(1)泡沫金属热导率较高,能够有效提高熔盐蓄热速率和对应的温度场均匀性,且孔隙率越小,泡沫金属支架越紧密,强化传热效果越好。在导热和自然对流复合阶段,孔隙率为85%时所对应的换热速率是纯硝酸盐的1.2 倍。同时泡沫金属支架会抑制液态熔盐自然对流,在蓄热后期熔盐基本熔化完全阶段,换热效果相比于纯硝酸盐较差。
(2)相同孔隙率和孔密度条件下,泡沫镍布置越靠近容器中心位置,中心处流动速度越小,对自然对流的抑制作用越强,换热效果越差。
(3)在导热和自然对流复合换热阶段,相同孔隙率和孔密度条件下泡沫铜所对应的换热速率比泡沫镍和泡沫铁要高,是纯硝酸盐换热速率的1.6倍。
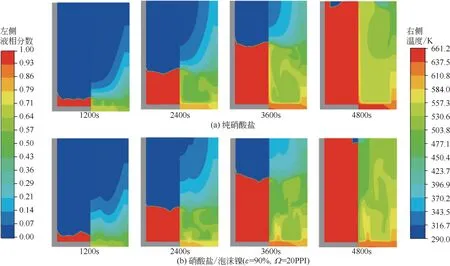
图11 熔盐蓄热过程液相率及温度分布
符号说明
Amush—— 固液共混区模糊常数,取值为105
a—— 泡沫金属多孔介质渗透率
asf—— 泡沫金属比表面积,m-1
Ci—— 泡沫金属多孔介质惯性阻力系数
cp—— 比定压热容,J/(kg·K)
g—— 重力加速度,m/s2
H—— 某一时间点的比焓,kJ/kg
hsf—— 泡沫金属与相变材料界面传热系数,W/(m2·K)
L—— 相变潜热,J/kg
peff—— 有效压力,Pa
Sx—— 轴向动量源项
Sr—— 径向动量源项
T—— 任意时刻温度,K
T1—— 参考温度,K
u—— 水平方向速度,m/s
v—— 纵向速度,m/s
x—— 轴向坐标,mm
α—— 熔盐的体积膨胀系数,K-1
β—— 液相率
ε—— 泡沫金属孔隙率
λ—— 热导率,W/(m·K)
μ—— 参考温度,K
ρ—— 密度,kg/m3
ρ1—— 熔盐的参考密度,kg/m
τ—— 时间,s
ω—— 阻止分母为0引入小于10-3的常数
下角标
f—— 泡沫金属
liquidus—— 熔化
s—— 熔盐
solidus—— 凝固
