NSGA-Ⅱ和NSGA-Ⅲ应用于换热网络多目标优化的对比

2020-07-25蒋宁范伟谢小东郭风元李恩腾赵世超

化工进展 2020年7期

蒋宁，范伟，谢小东，郭风元，李恩腾，赵世超

（浙江工业大学机械工程学院，浙江杭州310023）

在过程工业中，换热网络作为能量回收子系统，对其进行优化设计和改造，帮助企业增产、节能降耗、降低成本、减少污染排放等具有重要意义。换热网络优化本质上是多目标优化问题，需要综合考虑经济性、环境影响、能耗等。传统的换热网络多目标优化是采用一些数学方法将多目标函数变成单目标函数，然后将多目标优化问题简化成单目标优化问题进行求解，常用的方法主要包括加权求和法、ε-约束和NIMBUS 等[1]。Jin 等[2]将换热网络研究中的经济性和环境影响度两个目标量纲为1化，通过加权求和的方法，将多目标优化问题简化为单目标优化问题，实现污染排放量下降68.07%。Francesconi 等[3]采用ε-约束简化乙醇生产的换热网络，优化制氢效率和换热面积两个目标，可以实现最大面积减少50%，制氢效率下降1%。Lauukkanen等[4]采用NIMBUS 交互式方法，将换热单元数、总换热面积、公用工程消耗量的多目标优化模型，简化成单目标优化问题，使案例的总费用下降32%。Sreepathi和Rangaiah[5]通过数据研究表明换热面积、换热单元数和公用消耗三个经济目标存在相互竞争的状态，单纯的单目标优化不能满足实际工况的需求，多目标优化得出的Pareto解集能够提供综合考虑的方案。

Deb[6]提出了基于非支配排序的NSGA-Ⅱ算法，该算法能够高效快速地求解多目标优化问题，已被广泛应用到换热网络的多目标优化研究中。Agarwal 和Gupta[7]将NSGA-Ⅱ首次引入到换热网络的优化改造，并发现多目标优化得到的非支配解集的效果优于单目标优化的唯一解的效果。Sreepathi和Rangaiah[8]提出再分配策略以适应实际的换热网络改造问题，针对投资成本和公用成本建立的多目标模型，采用NSGA-Ⅱ算法求解，最终得到了Pareto解集，该解集能够给决策者提供更多样的综合方案。Lü 等[9]等考虑了年度总成本和系统可靠性，应用NSGA-Ⅱ求解提出的多目标模型，可以通过年度成本的小幅增加来实现换热网络耦合度的显著降低。林露[10]综合考虑了环境影响量、公用工程费用和投资费用的多目标优化模型，采用NSGA-Ⅱ算法得到Pareto前沿解，获得了相对于文献具有更低年度总费用的解，同时也提供了多个备选方案。

在超过3个目标的高维多目标优化问题的研究中，NSGA-Ⅱ存在收敛性较差的问题，因此学者们引入了基于参考点选择机制的NSGA-Ⅲ算法，计算目标数较多的多目标优化问题，以有效降低计算复杂度。研究表明，NSGA-Ⅲ在求解3～15个目标优化问题时具有良好的表现[11]。Wang等[12]为了提高钢铁工业的产业体系整体性能，建立了最小化能耗、5 种污染物的减少量和经济成本共7 个目标的多目标优化模型，采用了NSGA-Ⅲ和模糊C 均值聚类算法，给出了最佳的环境管理决策。对于NSGA-Ⅱ和NSGA-Ⅲ两种算法在求解不同的多目标问题的性能比较仍需进一步研究。Ishibuchi 等[13]用DTLZ来测试NSGA-Ⅱ和NSGA-Ⅲ的性能，在多目标的测试问题上NSGA-Ⅲ并不总是优于NSGA-Ⅱ，不同的测试问题对计算性能和结果的影响要大于目标数量的影响。Ciro 等[14]采用NSGA-Ⅱ和NSGA-Ⅲ对生产系统中作业的总流动时间、人和机械的工作负载的多目标模型进行优化，对于小尺寸实例，两种算法具有相似的性能，对于大尺寸实例，NSGA-Ⅲ比NSGA-Ⅱ有更好的性能。

在不同的多目标优化问题研究中，两种算法会呈现不同的性能。换热网络优化问题是能源领域研究的重要问题，由于其不仅需要考虑到能耗、投资成本、公用工程费用等经济指标，还需要考虑环境影响、改造工程量等其他指标要求，特别是随着环境要求和市场竞争变得越来越严峻的形势下，对换热网络进行多目标优化时，需要考察和关注的性能指标也呈现出多样性的特点[15]。而优化算法是求解换热网络多目标优化问题的关键之一，迫切需要开展相关研究和讨论。单纯根据优化问题的目标数量而不综合考虑目标的相关性，直接采用NSGA-Ⅱ或NSGA-Ⅲ是不合理的。因此，本文基于换热网络多目标优化问题，结合具体的换热网络案例，对两种应用较为广泛的多目标优化算法，NSGA-Ⅱ和NSGA-Ⅲ，开展了性能对比研究，测试NSGA-Ⅱ和NSGA-Ⅲ两种算法应用于换热网络多目标优化的求解效果，考察不同数量目标下两种算法的收敛性和运算效率，探索NSGA-Ⅱ算法应用于3个以上目标的优化问题的可能性，并比较NSGA-Ⅱ和NSGA-Ⅲ获得的解集方案的实际效果。相关研究结果也可为能源领域其他多目标优化问题的研究和优化算法选择提供参考。

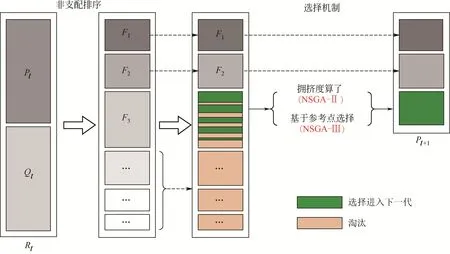
图1 NSGA-Ⅱ和NSGA-Ⅲ的选择机制

1 NSGA-Ⅱ和NSGA-Ⅲ原理

NSGA-Ⅱ和NSGA-Ⅲ算法如图1 所示。NSGA-Ⅱ和NSGA-Ⅲ是基于基本遗传算法，通过引入Pareto机制和非支配解的概念，形成了区别简单遗传算法的选择机制[16]。该选择机制充分利用个体间的支配和非支配关系，对种群进行分层，非支配层越高的个体被选择的概率越大；同时，为了丰富种群的多样性，NSGA-Ⅱ通过引入拥挤度算子[17]或聚类算子[18]来计算个体之间的拥挤度距离，如图2 所示；NSGA-Ⅲ[11,19]则通过引入参考点，表示期望的理想解，并通过关联和小生境操作，忽略目标空间中距离较近的解，从而得到一组靠近参考点的优化解集，如图3所示。

1.1 NSGA-Ⅱ拥挤度距离算子

NSGA-Ⅱ为了实现在执行选择的过程中，同一层的个体会因较大的拥挤度距离有更高的概率被选入到下一代的种群中，个体拥挤距离是目标空间上与i 相邻的2 个体i+1 和i-1 之间的距离如图2 所示，其计算步骤如下[17]。

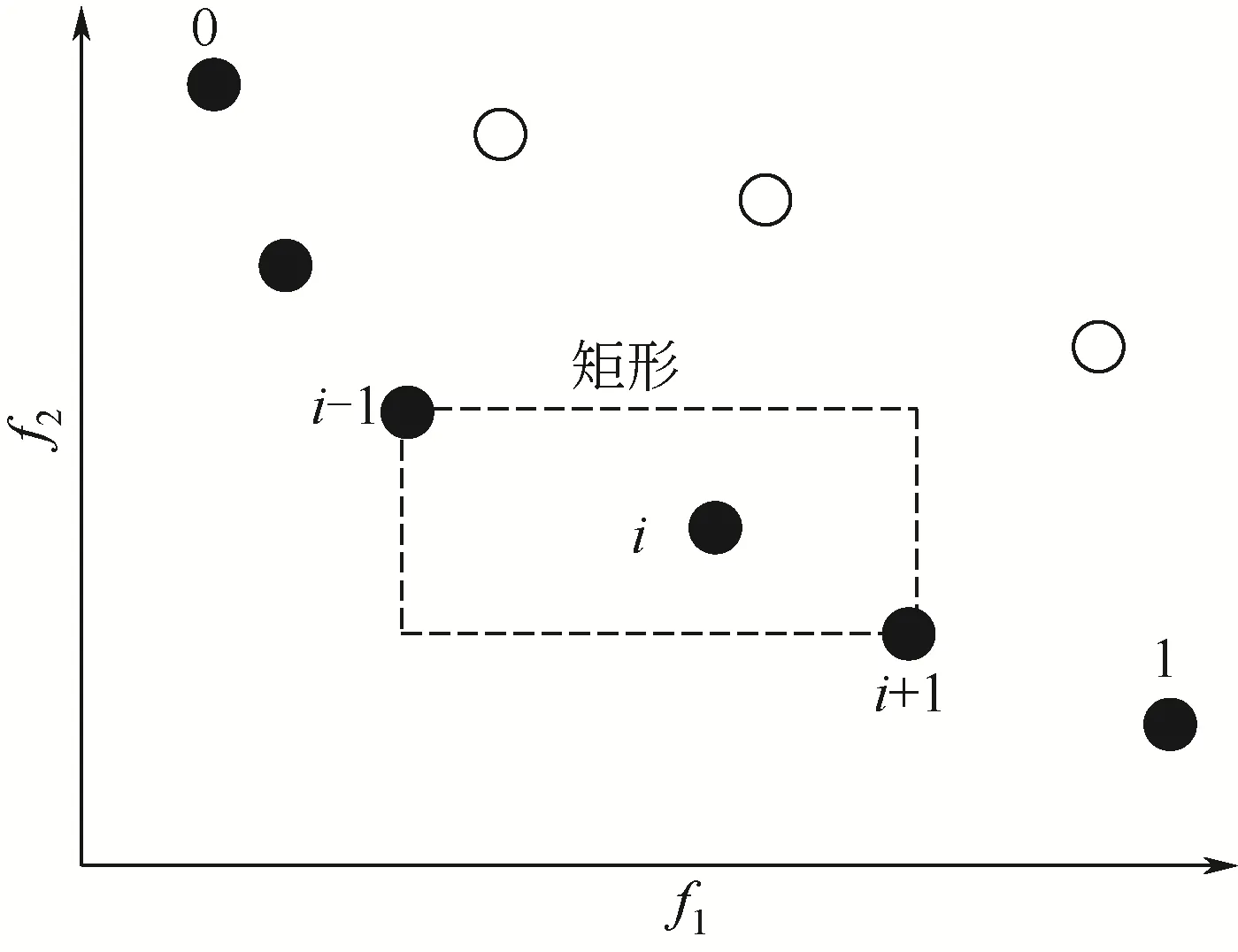
图2 拥挤距离计算

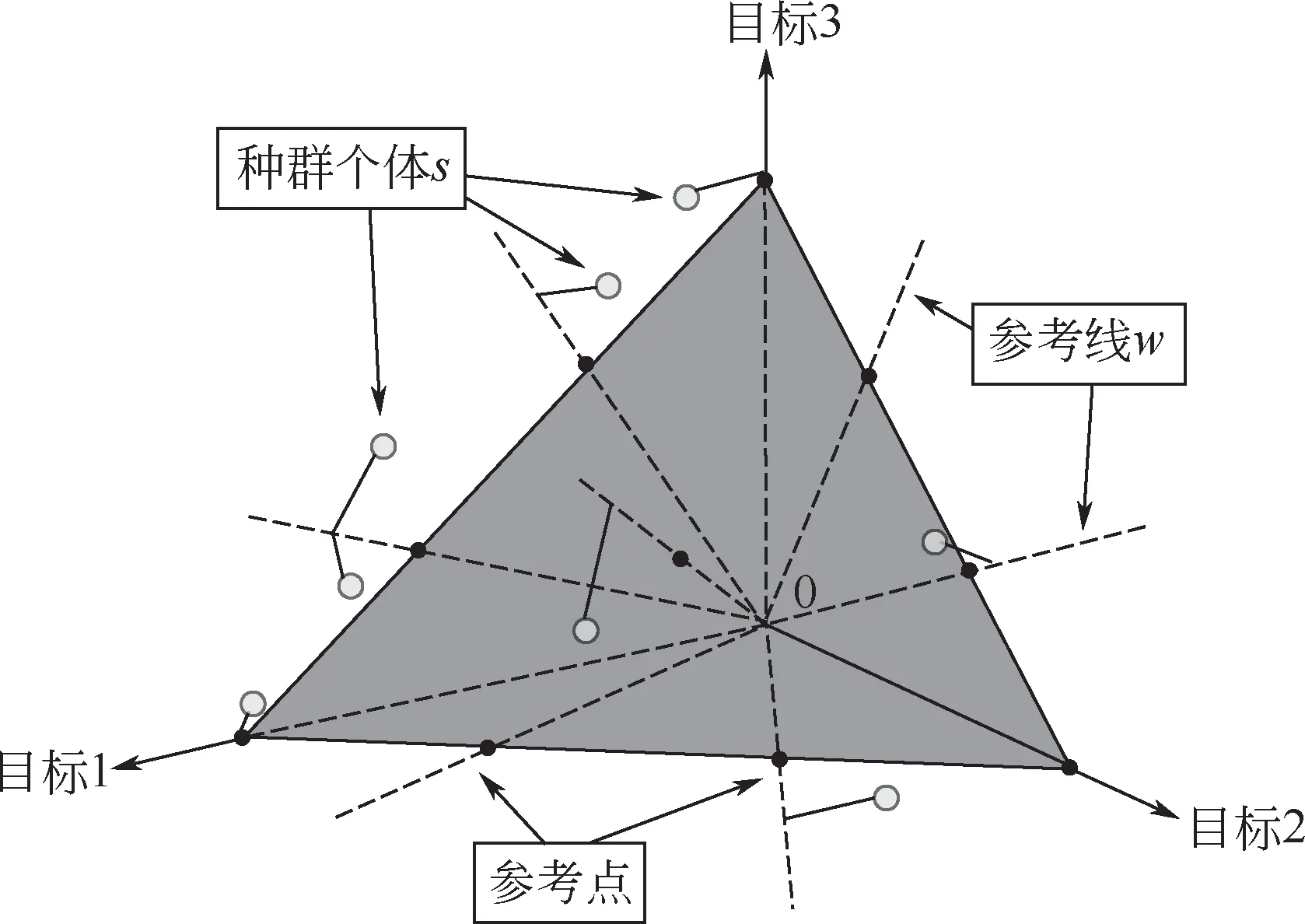
图3 参考点机制

（1）对同层的个体初始化距离。令L[i]d=0，其中L[i]d表示任意个体i的拥挤距离。

（2）对同层的个体按第m个目标函数值升序排列。

（3）排序边缘上的个体具有选择优势，令L[0]d=L[I]d=∞。

（4）对排在中间的个体，求拥挤距离，可由式(1)得到。

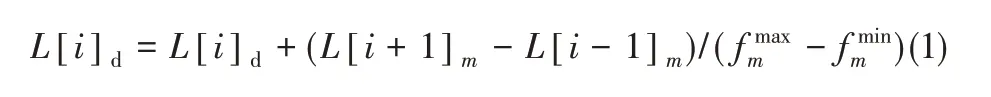
其中，L[i+1]m为第i+1个体的第m目标函数值，和分别为集合中第m 目标函数的最大值和最小值。

（5）对不同的目标函数重复步骤(2)～(4)，得到个体i 的拥挤距离L[i]d，通过优先选择拥挤距离较大的个体，使计算结果子目标的空间分布比较均匀，以维持种群的多样性。

1.2 NSGA-Ⅲ参考点机制

引入基于参考点的NSGA-Ⅲ，通过预先定义跨越整个Pareto前沿的一组搜索方向，并且每个方向执行多次搜索，从而获得广泛分布在Pareto最优前沿上的最佳解集；同时预定义多个参考点来替代搜索方向，利用对应于每个参考点的解以获得广泛分布的Pareto最优解集，其中归一化操作是参考点机制的核心，具体步骤如下[11,19]。

（1）计算理想点，针对M 维的多目标优化问题，分别求取种群在目标每个维度上的最小值，将这些最小值zi,min构成的集合定义为理想点集Zmin[式(2)]。

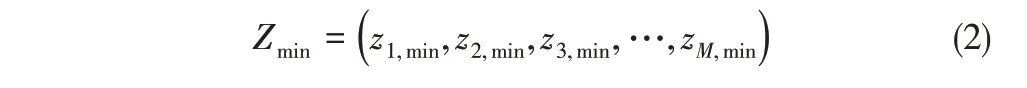
（2）转译目标值fi´(x)[式(3)]，为创建线性超平面并求取每个目标轴上的截距，采用St目标值f1减去每个目标的理想点zm,min的方法对所有目标值进行转译，得到转译种群S′t。

（3）计算各目标的极值点zi,max，采用标量化函数（ASF）计算出每个目标值在某i 维目标方向上的投影值并找出每个x在第i维目标的最大投影值，从最大投影值中选择最值对应的x 为第i 维目标的极值点zi,max[式(4)]。

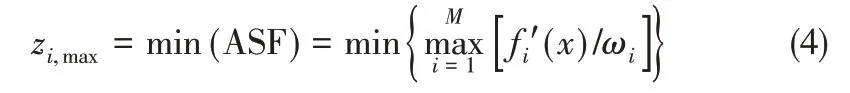
（4）构建线性超平面并计算截距ɑi，实现种群个体目标值的归一化，根据线性超平面的通用方程[式(5)]将每个维度上的极值点Zmax代入上述方程，得到超平面具体的形式，进而求得该超平面与每个维度方向的截距ɑi。

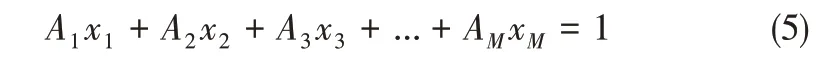
（5）种群目标值归一化，每个个体目标值归一化公式如式(6)。

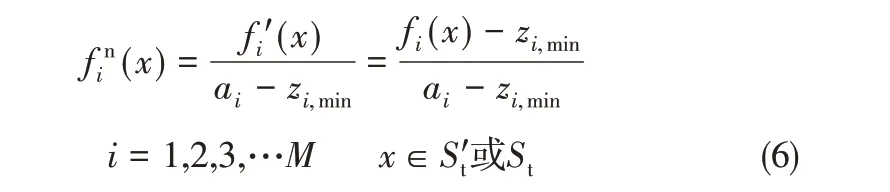
其中，上角标n表示归一化。

通过关联操作，在归一化的目标空间内，将距离种群个体s最近的参考线w对应的参考点定义与s关联。种群个体与参考点关联示意图（以3维目标10个结构化参考点为例），如图3所示。

2 换热网络的多目标优化改造问题

2.1 模型与约束

本文沿用Yee 和Grossman[20]所提出的分级超结构模型，同时取消了超结构模型中的非等温混合假设。本文优化改造满足热平衡约束、质量守恒约束、传热方程、过程物流非等温混和能量平衡、流股的入口温度约束、可行性温差约束、最小传热温差约束[21]。

2.2 目标函数

换热网络优化改造问题，通常涉及的性能评价指标包括以下方面。

（1）最小能耗

换热网络需要在冷、热流股末端配置公用工程换热器，以实现流股终端温度符合工艺要求。其中，公用工程换热器的能耗反映了换热网络需要消耗多少公用工程负荷，包括热公用工程负荷和冷公用工程负荷。其表达式如式(7)所示。

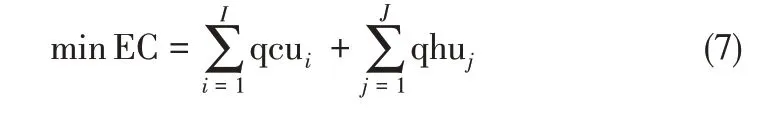
式中，qcui、qhuj分别表示第i股热过程流体上的冷公用工程负荷、第j 股冷过程流体上的热公用工程负荷。

（2）最小环境影响量

本文基于ISO 14040/44，采用LCA方法中最新的ReCiPe 指标[22]进行建模，环境影响数据取自于EcoInvent v 3.2 生命周期清单数据库。对于冷公用工程（通常为冷却水），将原始数据的单位转化为points/(kW·a)以便案例使用。为简化模型的复杂程度，此处假设所采用的换热器的材料均为不锈钢，设备运行时间为8000h/a，换热器的质量（mex）可由式(8)计算得到。

式中，A、δ 和D 分别代表换热器面积、厚度和不锈钢密度；根据文献[20]推荐，厚度δ 和不锈钢密度D分别取5.0×10-3m和7900kg/m3。

本文建立的环境影响目标函数，其包括冷、热公用工程的产生以及换热器的生产所带来的环境影响。可由式(9)计算得到。

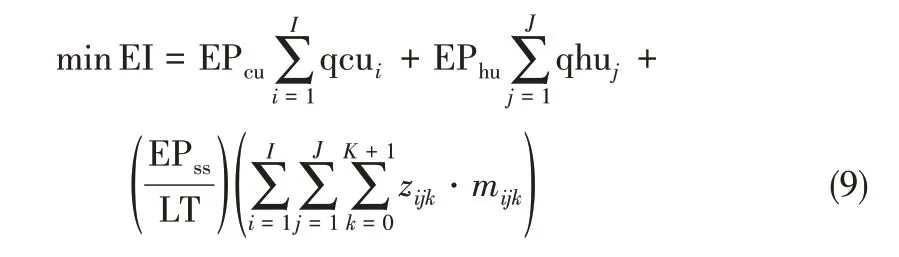
式中，EP、m 和LT 分别表示生态点值、换热器质量和设备使用年限；z 表示换热器存在与否的二元变量；下角标cu、hu 和ss 分别表示冷、热公用工程和不锈钢（stainless steel）。

（3）改造工程量

改造工程量（retrofit engineering quantity，REQ）指标，反映对现有换热网络实施不同的改造工程的相对难易程度。换热网络改造过程一般包括：新布管、移动原有换热设备、改变物流间的匹配关系、原有换热设备面积的增减和新增换热器等。根据实际的换热网络改造所面临的工况，并根据是否增加新的匹配关系。具体的改造工程量分为：回用原网络的换热器（包括增加面积和减少面积两种情况）、移动回用的原网络的换热器（包括用于原有匹配关系和新增匹配关系两种情况）、需要新增换热器（包括用于原有匹配关系和新增匹配关系两种情况）和设置旁路，每种改造工程需要的工程量系数见表1。则总的改造工程量可由式(10)计算得到：

其中，w1、w2、w3、w4、w5、w6和w7分别代表7个分项的工程量系数（表1）；n1、n2、n3、n4、n5、n6和n7分别代表7个分项以自然计数单位表示的需要实施的改造工程量。

（4）最小年度投资费用

换热网络改造过程的投资成本（capital cost，CC），包括现有换热器增加面积的改造费用、新增换热器的费用，其函数表达式如式(11)所示。

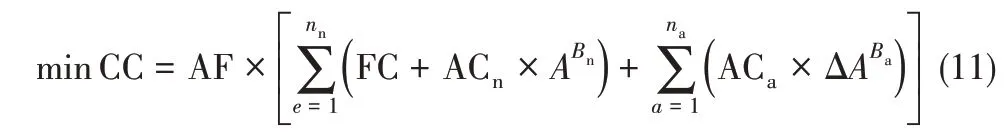
式中，nn、na分别代表新增换热器数目和增加面积的现有换热器数目；FC、ACn、Bn和ACa、Ba分别代表新增换热器的成本计算参数和现有换热器增加面积的成本计算参数；AF 是指改造投资费用的年度因子，其计算方法如式(12)。

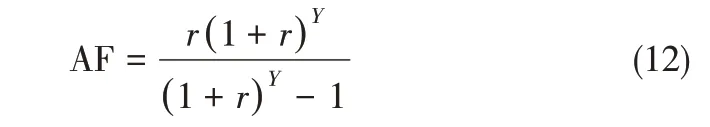
其中，r、Y分别代表年利率和使用年限。

（5）最小年度公用工程费用

公用工程费用（utility cost，UC）包括热公用工程的消耗费用和冷公用工程所带来的费用，其目标函数如式(13)所示。

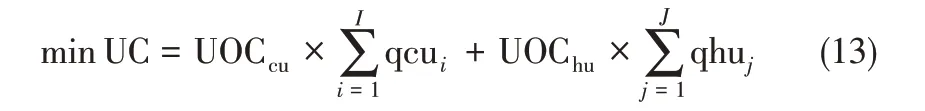
式中，UOCcu、UOChu分别表示冷、热公用工程的单位操作成本；qcui、qhuj分别表示第i股热过程流体上的冷公用工程负荷、第j 股冷过程流体上的热公用工程负荷。

（6）最小年度总费用

年度总费用（total annual cost）一般由公用工程费用和投资费用两部分构成。换热网络改造通过增加新的设备投资，尽可能经济地回收物流的有效能量，以达到减少公用工程能耗的目的。从操作成本和投资成本的角度综合权衡，得到换热网络的总费用，可由式(14)计算得到。

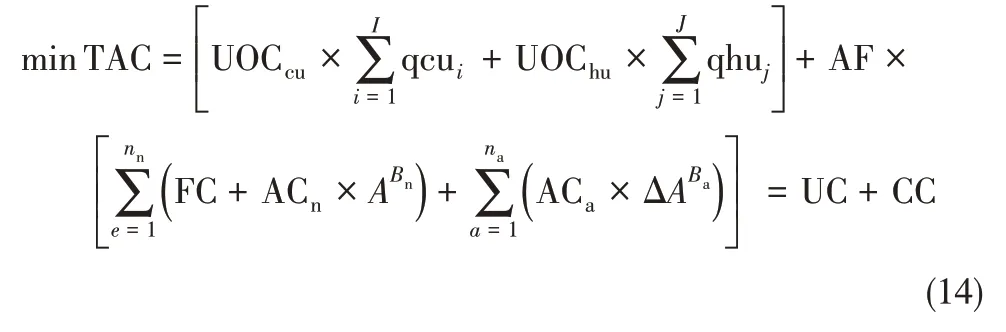
3 案例及性能分析

将NSGA-Ⅱ和NSGA-Ⅲ两种多目标算法应用于换热网络多目标优化问题的研究，比较两种算法的收敛性、运算效率、解集分布和案例结果。本文的NSGA-Ⅱ和NSGA-Ⅲ算法基于MATLAB2018b编写，初始参数设定为：种群大小为200，最大进化代数200，交叉和变异概率分别为0.8和0.005。

3.1 案例1

本文对文献[23]的原油蒸馏系统进行研究，案例包含10条热物流和5条冷物流，其物流数据与相关费用参数如表2和表3所示，初始的换热网络结构图如图4 所示。原始换热网络消耗热公用工程9.537×104kW/a，冷公用工程5.792×104kW/a，环境影响量为1.797×107pts/a，产生的公用工程费用为1.393×107USD/a。

表1 分项间的工程量换算系数

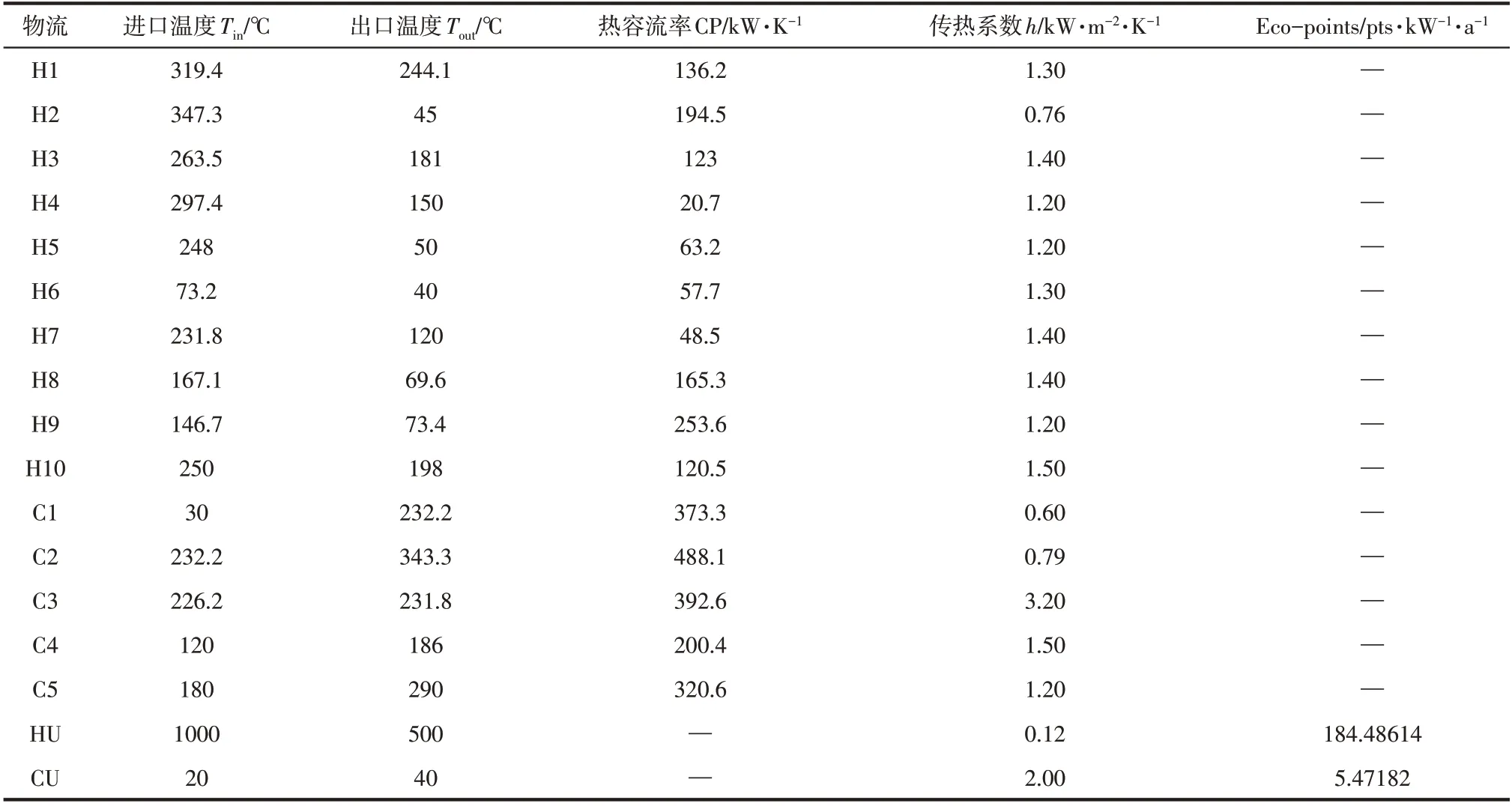
表2 物流数据参数及生态点取值

表3 各项费用的相关参数

3.1.1 收敛性比较

通过选择测试不同数量的目标，研究NSGA-Ⅱ算法和NSGA-Ⅲ算法在不同目标数量的换热网络优化中的收敛性，采用每一代所有个体的平均欧式距离来衡量迭代的收敛程度。如图5和图6为不同数量的目标情况下NSGA-Ⅱ和NSGA-Ⅲ两种算法的收敛曲线，可以看出欧式距离随着迭代次数的增加，欧式距离的值最终趋于0，最终收敛曲线越来越平缓，这说明在迭代过程中，NSGA-Ⅱ和NSGA-Ⅲ两种算法都逐渐收敛，解集逐渐趋于稳定。从图5所示的NSGA-Ⅱ算法的收敛曲线，目标个数为2、3、4个时，NSGA-Ⅱ算法的收敛速度都比较快，进化约30～40 代，已基本收敛；在算法初期，目标数为2个和3个时的收敛趋势优于目标数为4 个时的情况；目标个数为2、3、4 个时，NSGA-Ⅱ算法最终都能实现较好的收敛效果。从图6所示的NSGA-Ⅲ算法的收敛曲线，目标数为2个和4个时的收敛速度比目标数为3个时更快；目标数为2和4个时，进化约50代之后基本收敛，而目标数为3 个时，进化150 代之后才收敛；目标个数为2、3、4个时，NSGA-Ⅲ算法最终也能达到较好的收敛效果。Deb等[11]认为NSGA-Ⅲ在求解大于3个目标的优化问题有良好表现，而NSGA-Ⅱ不具备优化大于3个目标的优化问题的能力。如图7所示，NSGA-Ⅱ算法在求解4个目标的换热网络多目标优化问题时，算法也可以实现收敛；用NSGA-Ⅱ求解能耗、环境影响量、公用工程费用以及年度总费用4个相关性较高目标的优化问题时，其收敛性优于NSGA-Ⅱ求解环境影响量、改造工程量、投资费用和公用工程费用4个目标相关性较低的优化问题的收敛性，收敛曲线更加平滑。NSGA-Ⅲ算法在求解4个目标相关性较高和相关性较低的多目标优化问题，都能保证收敛；而NSGA-Ⅱ算法的收敛性则受目标相关性和目标数量的共同影响。由于NSGA-Ⅲ算法采用了基于参考点的选择机制，在高维目标的收敛性要明显优于NSGA-Ⅱ算法。因此，对于换热网络多目标优化问题，NSGA-Ⅱ算法的应用并不严格地受限于3个目标的最大目标数量，NSGA-Ⅱ在求解大于3个目标的多目标优化问题时也可能具有良好的性能，目标数量并非选择NSGA-Ⅱ和NSGA-Ⅲ算法严格标准，特别是对于相关性较高的多目标优化问题，可以采用NSGA-Ⅱ算法实现快速寻优。

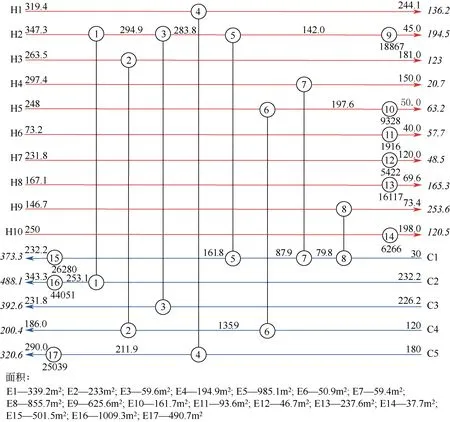
图4 案例1现有原油蒸馏系统换热网络拓扑结构

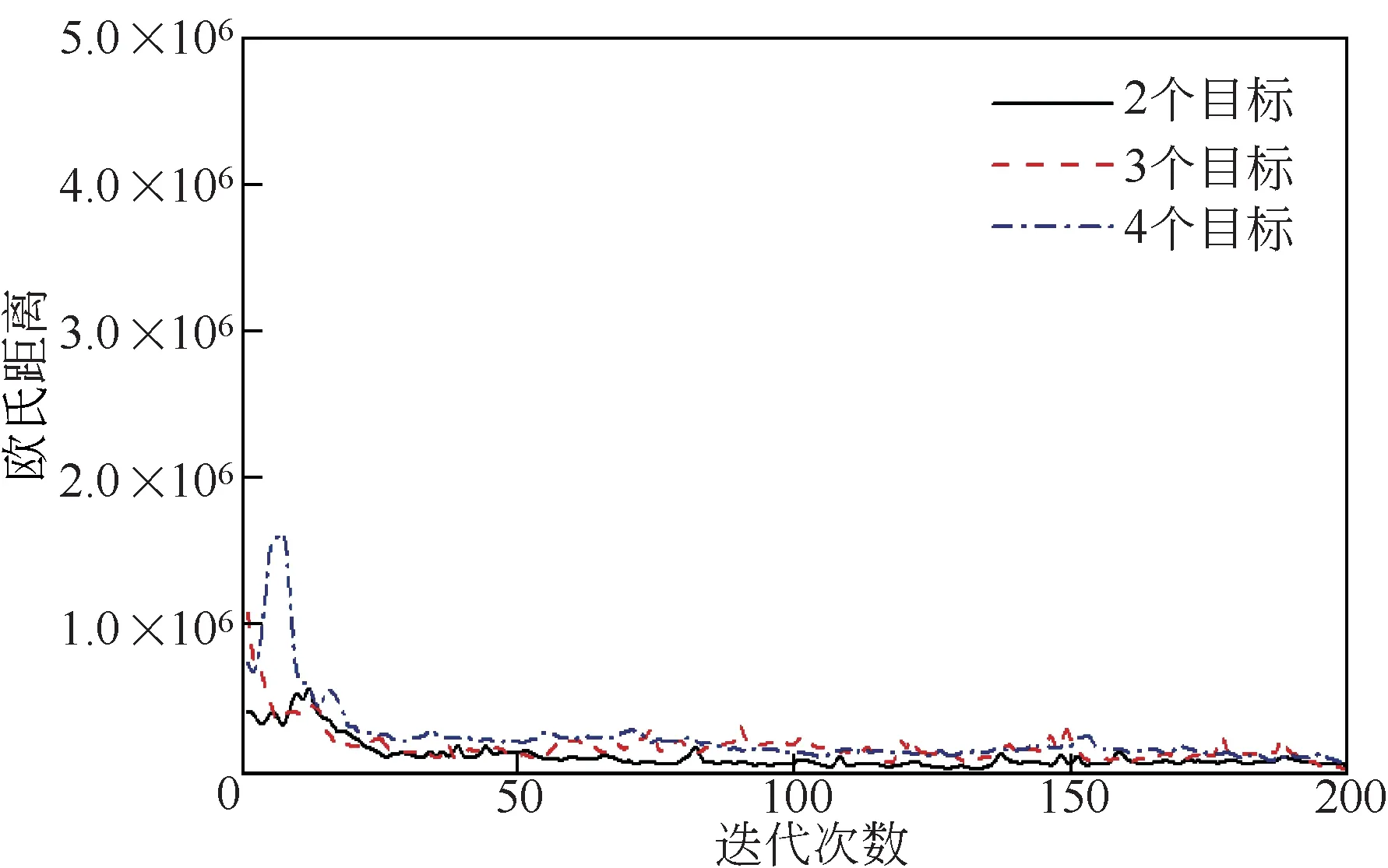
图5 NSGA-Ⅱ的收敛曲线

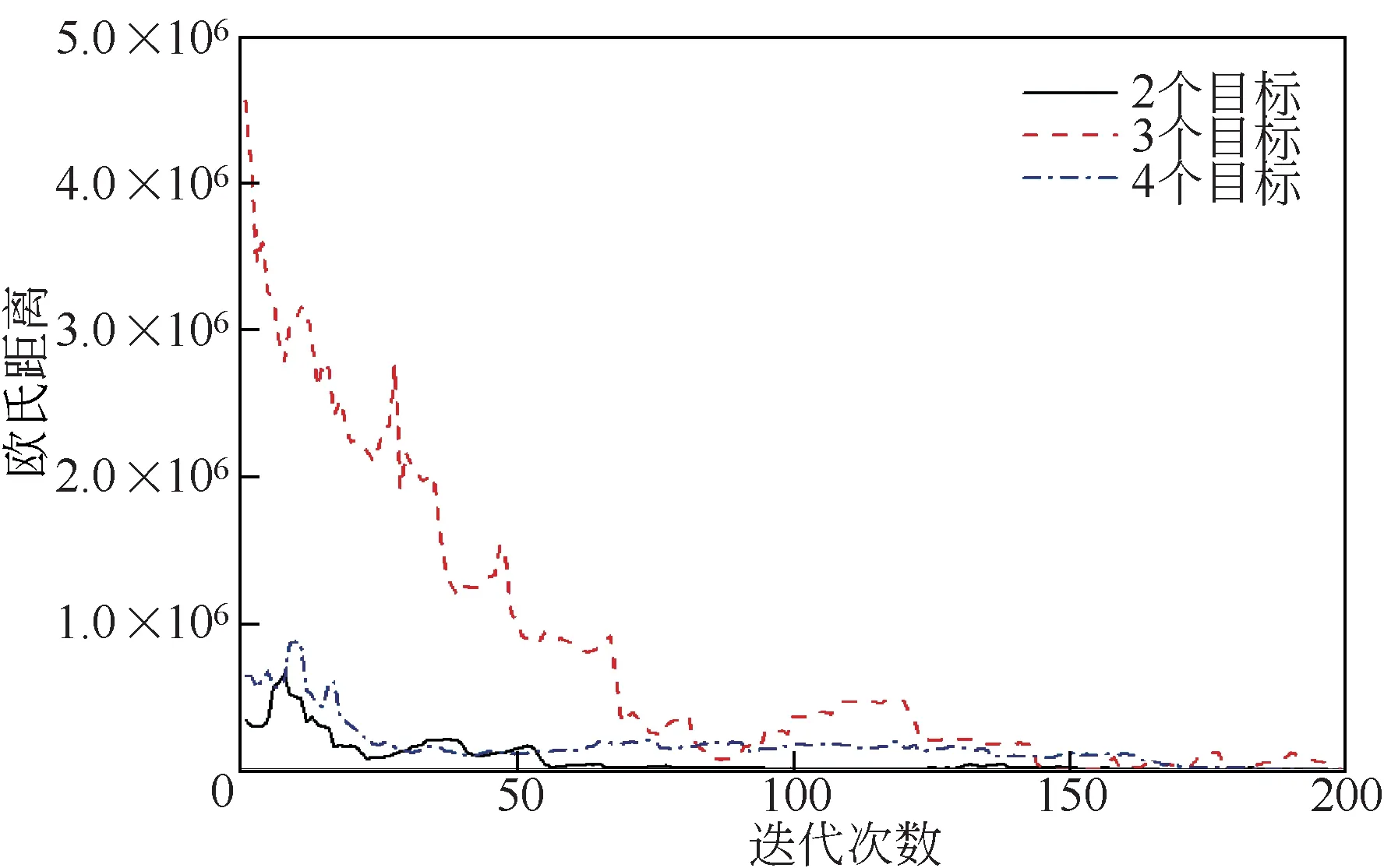
图6 NSGA-Ⅲ的收敛曲线

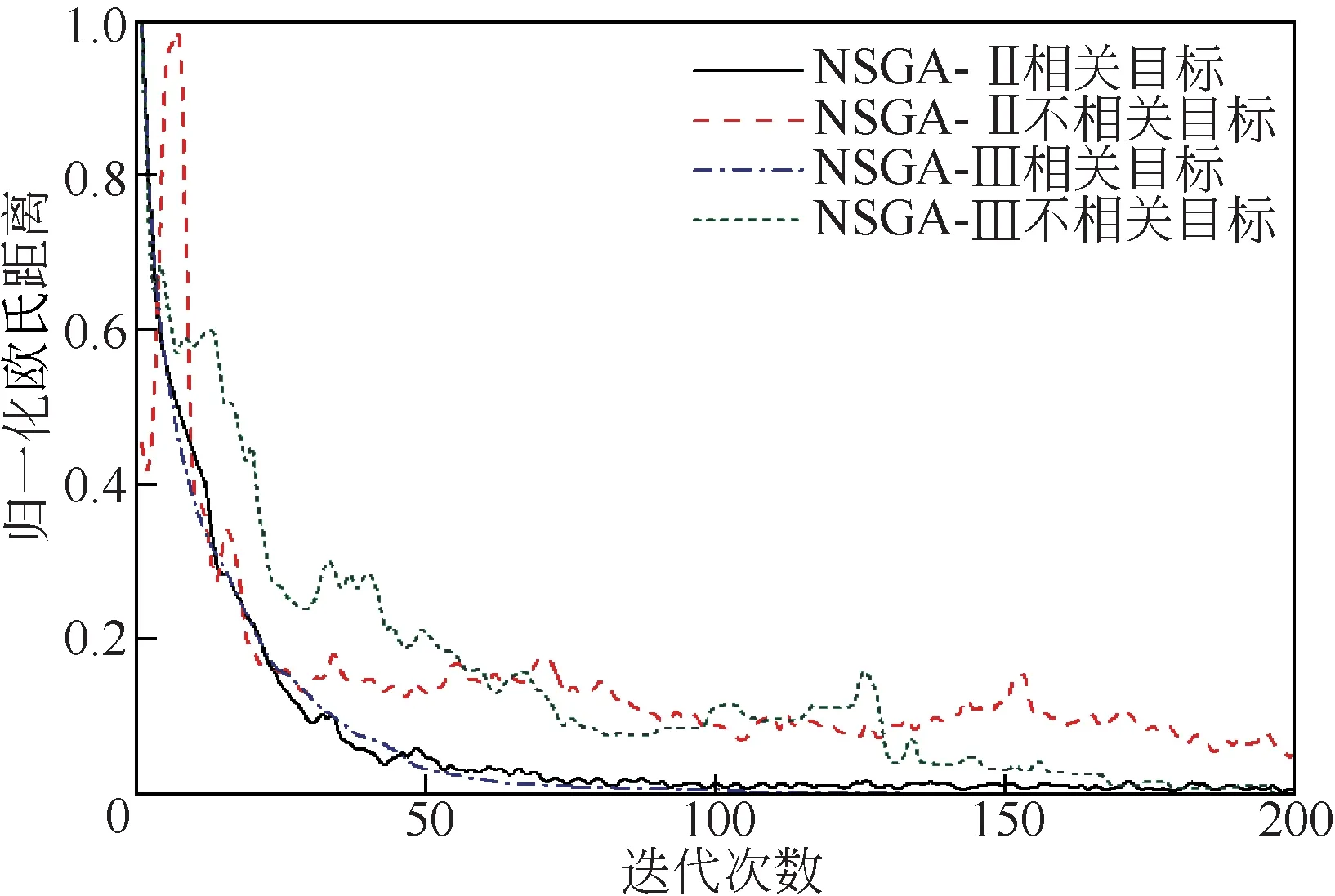
图7 NSGA-Ⅱ和NSGA-Ⅲ算法用于4个相关目标和不相关目标的收敛曲线

3.1.2 运行效率比较

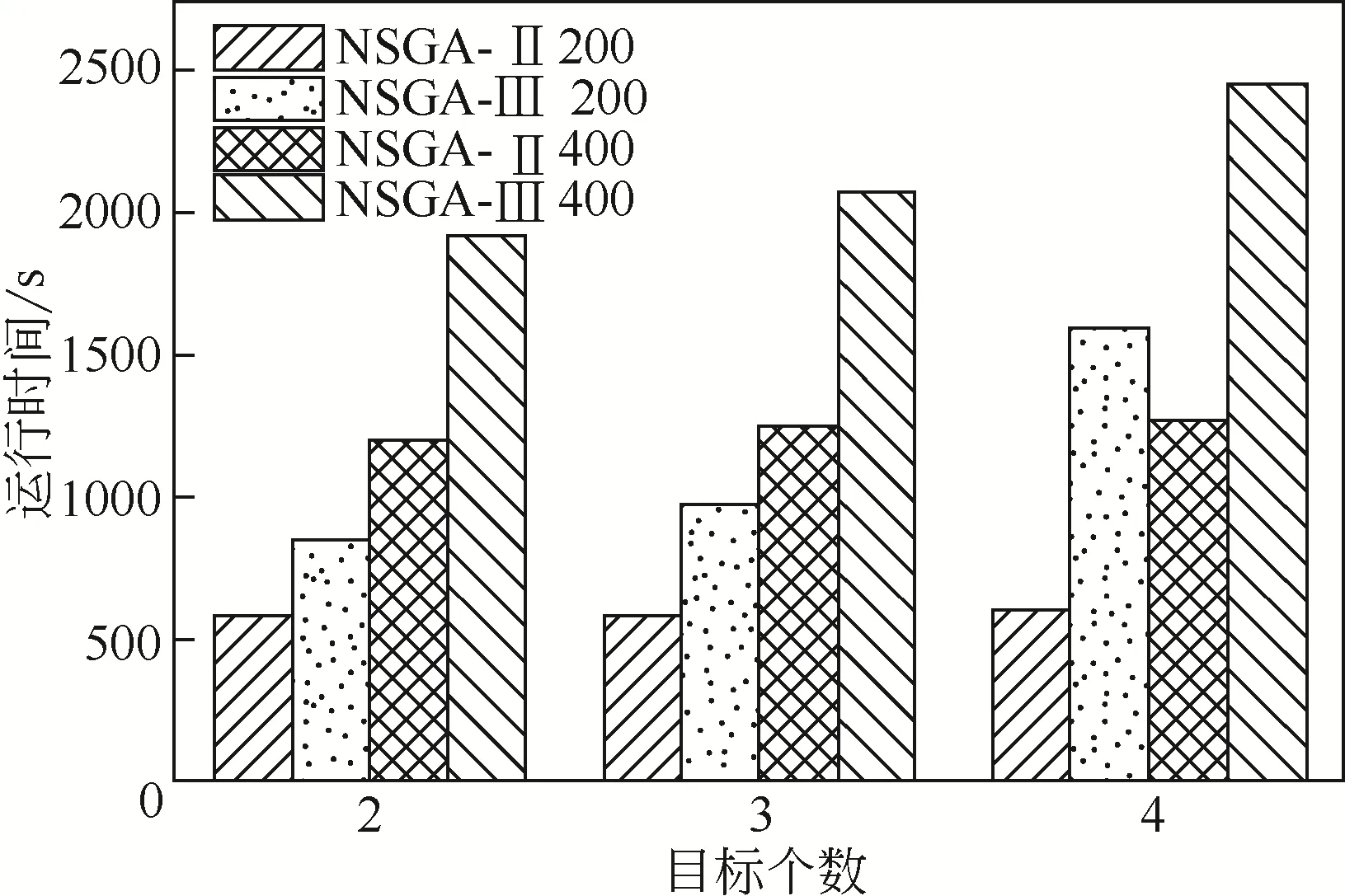
图8 NSGA-Ⅱ和NSGA-Ⅲ运行时间的关系图

如图8 所示，NSGA-Ⅱ在种群数量200 的条件下，目标数为2、3、4的运行时间持平；同时随着种群数量增多后，例如在种群数量为400 的条件下，不同目标数的运行效率的差距不大。NSGA-Ⅲ在种群数量200 的条件下，目标数为2、3、4 的运行时间差距较大，尤其是在目标数为4 的条件下，运行时间是目标数为2的运行时间的近2倍；当种群数量增加到400 时，目标数为2 的运行时间已高达1930s，是种群200、目标数为2 的运行时间的2.3 倍。相同的种群数量，NSGA-Ⅲ的运行效率要远远小于NSGA-Ⅱ的运行效率，在目标数为4，种群数量为200时，NSGA-Ⅲ的运行时间是NSGA-Ⅱ的2.7 倍；在目标数为4，种群数量为400 时，NSGA-Ⅲ的运行时间时NSGA-Ⅱ的2.1倍。在目标数为2和3的条件下，随着种群数量的增加，两种算法之间的运算时间差距越来越大。在目标数为4的条件下，随着种群数量的增加，两种算法之间的运算时间差距变化不大，这主要是因目标数量增加带来的计算复杂度已超过种群数量计算所带来的影响。

3.1.3 解集分布及目标之间关系

选取环境影响量、改造工程量、投资成本和公用工程费用4个目标，考察解集的分布和任意两个目标之间的关系，如图9 所示。图9(a)反映了环境影响量和改造工程量的关系，改造工程量随着环境影响量的增大而减小；从解集的分布情况来看，靠近原点的解集中，NSAG-Ⅱ得到的解集的数量更多，有利于获得更低的环境影响量和改造工程量。图9(b)反映了环境影响量和投资成本的关系，投资成本越大，整个网络结构变化较大，获得部分更节能的结构，所需要的冷热公用工程负荷更少，从而环境影响量更小。从解集的分布来看，NSGA-Ⅲ算法得到的解集更靠近原点，说明NSGA-Ⅲ解集中可以获得具有更低投资成本和环境影响量的解。图9(c)反映环境影响量和公用工程费用的关系，公用工程费用和环境影响量呈明显的线性关系，同时NSGA-Ⅱ和NSGA-Ⅲ都有数量相当的解集分布在更小的公用工程和环境影响量的范围。图9(d)反映了投资成本和改造工程量的关系，从图中无法看出这两个目标之间的关系，说明投资成本和改造工程量之间的相关性较低。图9(e)反映了改造工程量和公用工程费用的关系，随着改造工程量的增加，公用工程费用显著减小，这是因为改造工程量越大，对原始换热网络结构的调整越大，优化网络结构导致所需的公用工程负荷减少，从而降低了公用工程费用；从解集分布上来看，NSGA-Ⅱ算法的解集分布更靠近原点，更容易获得改造工程量更低和公用工程费用更小的解。图9(f)反映了投资成本和公用工程费用的关系，投资成本越大，公用工程费用越小，这主要是因为，对原始的网络通过新增换热器、增大换热器的换热面积以及重新布管所产生的费用越大，优化网络结构的效果也更明显，以此来实现更加节能的换热匹配布局；从解集分布上来看，NSGA-Ⅲ算法得到的解集更靠近原点，可以获得具有更低投资成本和公用工程费用的解。

3.1.4 目标函数性能的比较

从NSGA-Ⅱ和NSGA-Ⅲ两种算法优化得到解集中，选出各目标的最小值，结果见表4。单一目标的最小值反映出各个评价目标函数的极值情况。从单一目标上来看，NSGA-Ⅱ得到的最小能耗、最小环境影响量、最小改造工程量、最小投资费用和最小公用工程费用要比NSGA-Ⅲ要小，其中最小能耗减少1.4%，最小环境影响量减少1%，最小改造工程量减少25.2%，最小投资费用减少14%，最小公用工程费用减少1%。

图10 给出了采用NSGA-Ⅱ优化所得到的具有最小年度总成本的改造方案，其中物流上方正体数字表示温度的分布，单位为℃；斜体表示流股的热容流率；公用工程为冷热流股的出口的换热器；换热器面积括号内的数值为在原有换热器的基础上进行的面积增减值。从网络结构图中，可以看出该改造方案回用了15 台换热器，其中共增加换热面积180.17m2，共需费用11.21×104USD；新增5 台换热器，共需费用28.16×105USD；其中有15 台需要改变原有的匹配关系，但本案例原始网络未考虑布管和变动匹配所带来的费用，因此忽略该部分的成本。所以改造过程所带来的改造投资总费用为29.28×105USD，年度化投资费用为5.86×105USD/a。通过与原始案例相比，从节能的角度分析，改造后的换热网络每年所需的热公用工程为6.61×104kW/a，冷公用工程2.88×104kW/a，较原有换热网络分别减少了30.66% 和50.26%，总能耗减少了5.83×104USD/a，降至9.49×104kW/a，降幅为58.35%，公用工程费用减少至9.55×106USD/a。综上所述，该方案的投资回报期为0.22年。从环境角度分析，原有换热网络经优化改造后，环境影响量从1.797×107pts/a降低至1.24×107pts/a，降幅为30.76%。

表4 两种算法优化方案各目标最小值

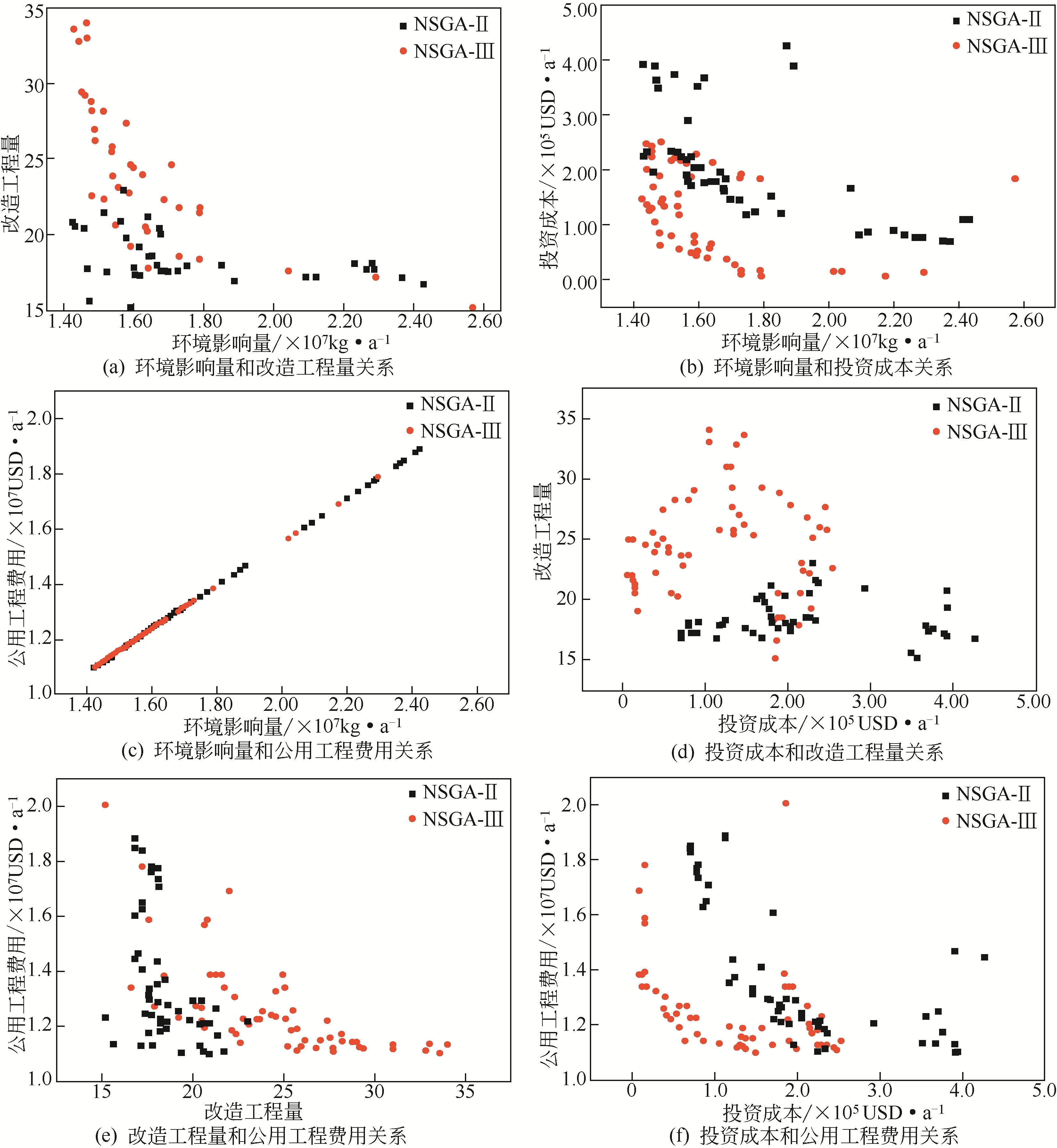
图9 NSGA-Ⅱ和NSGA-Ⅲ两种算法的目标函数的关系

将本文采用NSGA-Ⅱ和NSGA-Ⅲ算法优化的结果，与以往的文献进行对比分析，具体情况见表5。由表5 可知，与文献相比，采用NSGA-Ⅱ改造后的换热网络每年所需热公用工程减少16.75%～29.53%，冷公用工程减少31.10%～49.03%，因而年公用费用成本降低16.96%～30.65%，年度总费用TAC 减少14.15%～26.06%。采用NSGA-Ⅲ改造后的换热网络每年所需热公用工程减少15.87%～28.78%，冷公用工程减少29.43%～47.79%，因而年公用费用成本降低16.09%～29.92%，年度总费用TAC 减少14.75%～26.57%。从具有最小年度总费用的改造方案来看，NSGA-Ⅱ与NSG-Ⅲ获得的改造方案相比，热公用下降1%，冷公用下降2.3%，环境影响量下降0.4%，公用工程费下降0.5%，投资成本上升42.75%，年度总费用仅上升0.7%。

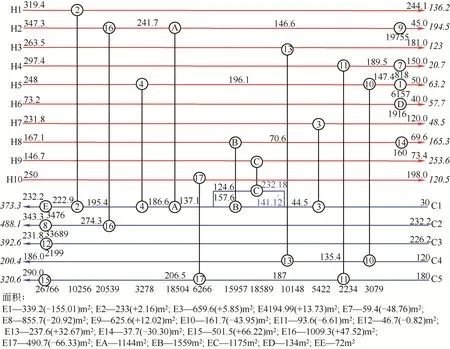
图10 案例1改造后的换热网络结构

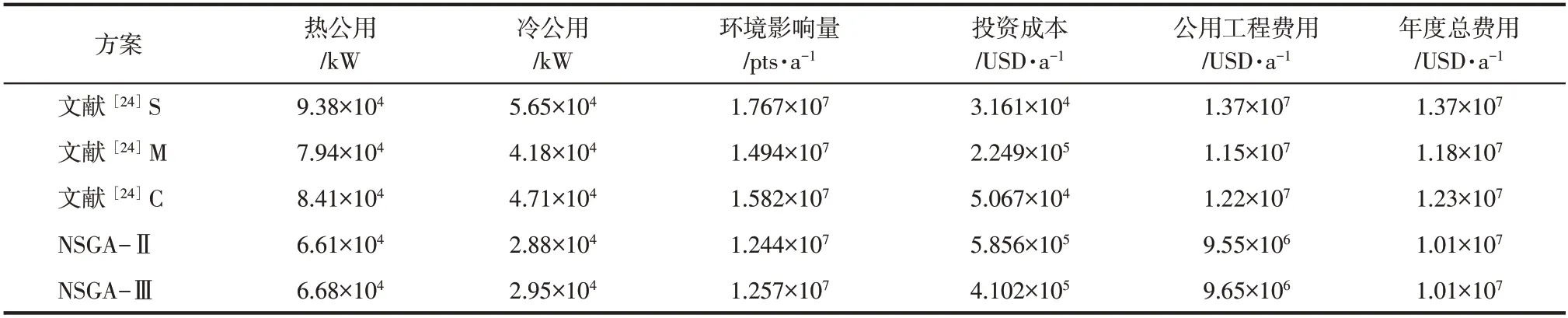
表5 改造结果与文献对比分析

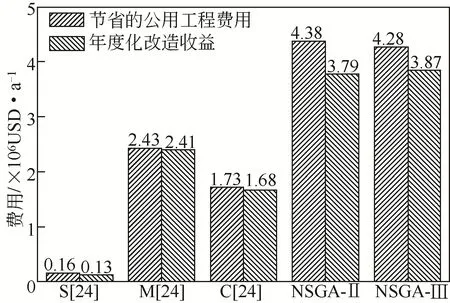
图11 本文工作与文献的经济性指标比较

从图11 可以看出，本文NSGA-Ⅱ的改造方案节省的公用工程费用和获得的年度化改造收益都比以往研究得到的改造方案更好，NSGA-Ⅱ的改造方案节省的公用工程费用要略优于NSGA-Ⅲ的改造方案，NSGA-Ⅲ改造方案的年度化改造收益要略优于NSGA-Ⅱ的改造方案。

3.2 案例2

本文对文献[25]的原油精馏系统进行研究，案例包含7条热物流和3条冷物流，其物流数据与相关费用参数见表6、表7，初始的换热网络结构图如图12 所示。原始换热网络消耗热公用工程1.0×105kW/a，冷公用工程6.6×104kW/a，环境影响量为2.289×107pts/a，产生的公用工程费用为6.33×106USD/a。换热器的总传热系数为0.4kW/(m2·℃)。

3.2.1 收敛性比较

对该换热网络建立高维多目标优化模型，综合考虑了能耗、环境影响量、改造工程量、年度投资费用、公用工程费用和年度总费用。NSGA-Ⅱ算法和NSGA-Ⅲ算法求解换热网络高维多目标优化模型的收敛性，如图13 所示。采用NSGA-Ⅲ算法得到的收敛曲线比NSGA-Ⅱ算法更加平稳，但两种算法都实现了收敛。该案例再次说明对于换热网络多目标优化问题，NSGA-Ⅱ算法的应用不严格地受限于目标的数量，对于6个目标的高维多目标换热网络优化问题，NSGA-Ⅱ也实现了收敛。

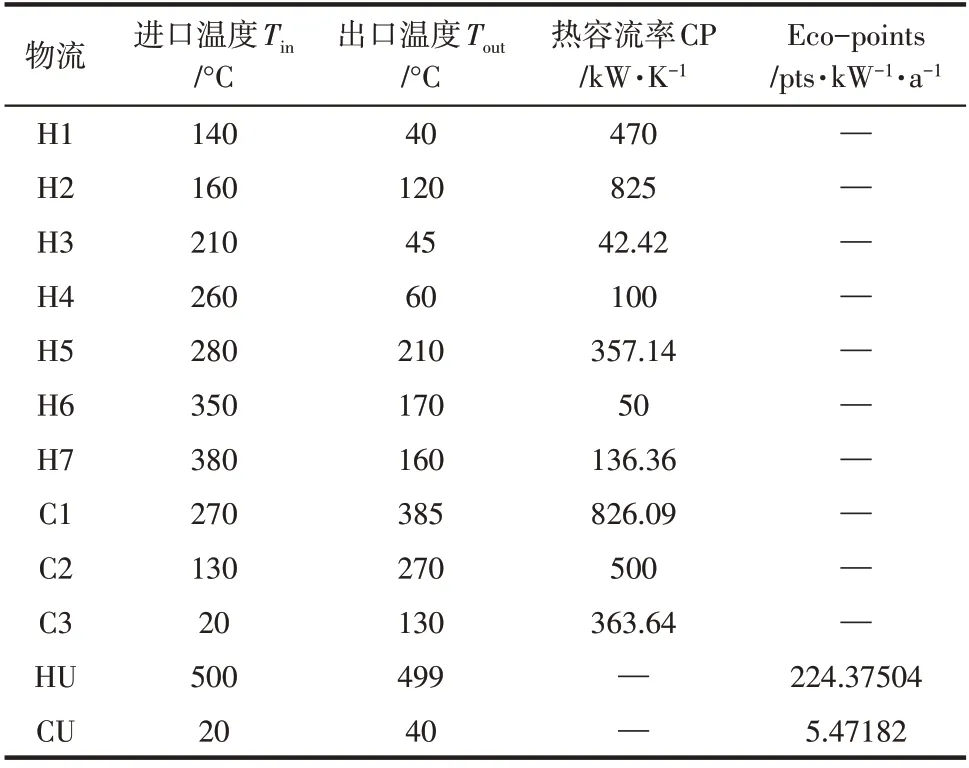
表6 物流数据参数及生态点取值

表7 各项费用的相关参数

3.2.2 目标函数性能的比较

分别采用NSGA-Ⅱ和NSGA-Ⅲ两种算法进行求解，得到各目标的最小值，结果见表8。从单一目标上来看，NSGA-Ⅲ算法得到的最小能耗、最小环境影响量、最小投资费用、最小公用工程费用和最小年度总费用这5 个目标的最小值均优于NSGA-Ⅱ算法得到的目标最小值，其中最小能耗下降3.0%，最小环境影响量下降2.4%，最小投资成本下降61.7%，最小公用工程费用下降2.5%，最小年度总费用下降3.3%。NSGA-Ⅱ算法的最小改造工程量为15.6，比NSGA-Ⅲ算法的最小改造工程量下降21.2%。

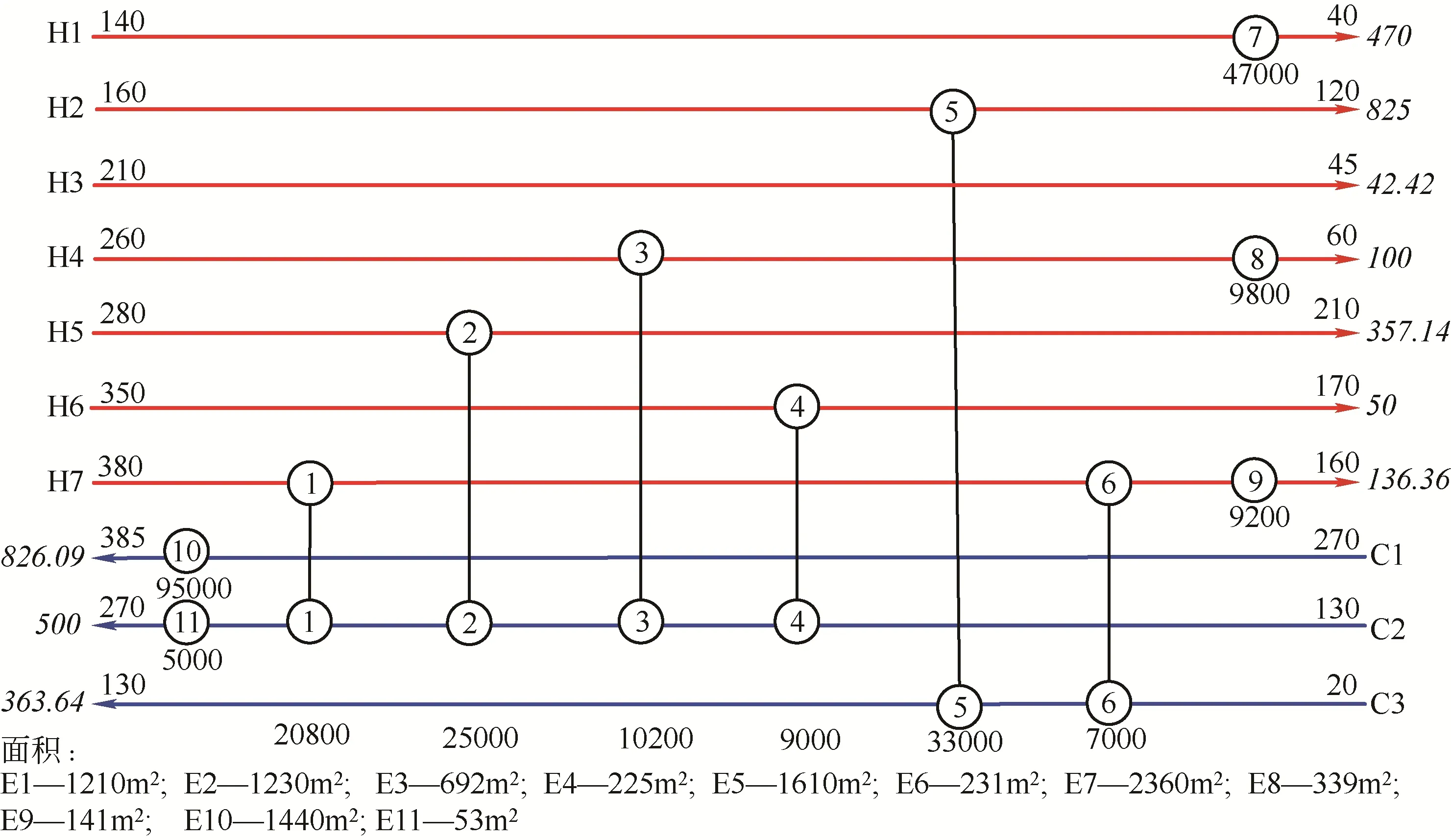
图12 案例2现有换热网络拓扑结构

表8 两种算法优化方案各目标最小值

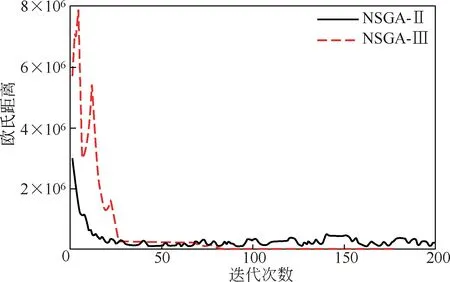
图13 案例2 中NSGA-Ⅱ和NSGA-Ⅲ算法的收敛曲线

图14 给出了采用NSGA-Ⅲ算法优化得到的最小年度总费用的改造方案，该改造方案回用了11台换热器，其中增加换热面积87.66m2，共需费用2.63×104USD；新增8 台换热器，共需费用4.46×105USD；移动和布管的费用共需2250USD，该改造方案的总投资费用为4.74×105USD，年度化投资费用为9.48×104USD/a。将NSGA-Ⅱ和NSGA-Ⅲ算法优化换热网络多目标问题得到的解集，选择最小年度总费用的方案与原文献进行对比分析，见表9。由表9 可知，与文献相比，采用NSGA-Ⅲ优化后的换热网络所需热公用工程减少9.2%，冷公用工程减少13.93%，环境影响量减少9.13%，公用工程费用减少9.48%，年度总费用减少8.1%，投资回报期为0.79a。与文献相比，采用NSGA-Ⅱ优化的改造方案所需热公用工程减少8.5%，冷公用工程减少12.88%，环境影响量减少8.69%，公用工程费用减少8.69%，年度总费用减少4.9%，投资回报期为2.23a。从两种算法获得的解集中选择最小年度总费用的改造方案，NSGA-Ⅲ的改造方案在投资成本和年度总费用明显优于NSGA-Ⅱ的改造方案，投资费用减少61.62%，年度总费用减少3.32%，投资回报期减少64.68%。

从图15 可以看出，对高维多目标的换热网络优化问题，采用NSGA-Ⅲ的改造方案节省的公用工程费用、节省的年度总费用和年度化改造收益均优于NSGA-Ⅱ的改造方案，节省的公用工程增加9.1%，节省的年度总费用增加64.5%，年度化改造收益增加5.6倍，高达4.15×105USD/a。

4 结论

本文针对换热网络多目标优化问题，研究比较了NSGA-Ⅱ和NSGA-Ⅲ两种算法的性能，结合具体的换热网络改造案例，考察了两种算法的收敛性、运算时间、解集分布和各目标之间的关系，对两种算法的性能和优化方案进行了深入讨论，并获得如下结论。

（1）目标之间的相关性应该被考虑到多目标算法的选择标准中。案例1 选取能耗、环境影响量、公用工程费用以及年度总费用4个相关性较高的目标建立换热网络多目标模型时，NSGA-Ⅱ算法具有更好的收敛性。案例2 选取能耗、环境影响量、改造工程量、年度投资费用、公用工程费用和年度总费用建立的高维多目标换热网络优化模型，NSGA-Ⅲ算法具有更好的收敛性。

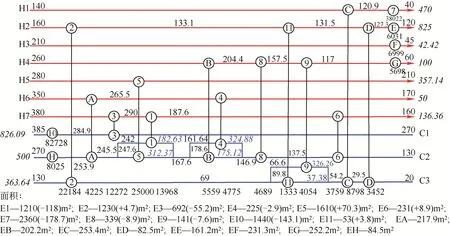
图14 案例2改造后的网络结构

表9 改造结果与文献的对比分析

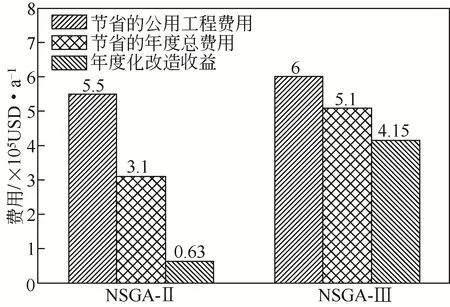
图15 案例2中NSGA-Ⅱ和NSGA-Ⅲ得到结果的经济性指标比较

（2）NSGA-Ⅱ运行效率受目标数量的影响较小，NSGA-Ⅲ运行效率受目标数量的影响较大。在种群数量较小、目标数量较小的条件下，NSGA-Ⅲ的运行效率略低于NSGA-Ⅱ；但在种群数量较大，或者目标数量增加的条件下，NSGA-Ⅲ的运行效率要远低于NSGA-Ⅱ，NSGA-Ⅲ的运算时间是NSGA-Ⅱ的2倍以上。

（3）10×5 换热网络案例研究表明，目标相关性较高的多目标优化问题，NSGA-Ⅱ比NSGA-Ⅲ更易获得各目标的最小值，根据最小年度总费用选择的综合方案，NSGA-Ⅱ与NSGA-Ⅲ获得的最优结果的效果相近，年度总成本仅相差0.7%。与文献相比，本文NSGA-Ⅱ和NSGA-Ⅲ均获得了年度总费用更低的改造方案，年度总成本分别下降了14.15%～26.06%和14.75%～26.57%。7×3 换热网络案例研究表明，对于高维多目标换热网络优化问题，NSGA-Ⅲ比NSGA-Ⅱ更易获得各目标的最小值，根据最小年度总费用选择的综合方案，NSGA-Ⅲ明显优于NSGA-Ⅱ，投资成本减少61.62%，年度总费用减少3.32%，投资回报周期减少64.68%。

符号说明

A—— 换热面积，m2

ΔA—— 现有换热设备增加的面积，m2

AF—— 投资费用年度化因子

AC—— 面积费用系数

B—— 面积费用指数

CC—— 投资费用，USD

D—— 不锈钢的密度，kg/m3

EC—— 能耗，kW

EI—— 环境影响量

EP—— 生态点值

FC—— 新增换热设备的固定费用，USD