采用Gompertz函数的水稻土压缩特性研究

霍连飞，Belal Eisa Adam，丁启朔※，何瑞银，汪小旵

（1. 南京农业大学工学院/江苏省智能化农业装备重点实验室，南京 210031； 2. 扎林盖大学农业工程系，扎林盖 999129）

0 引 言

农业机械田间作业引起的土壤压实对土壤物理力学性质和土壤结构、作物生长和产量以及农业生态环境的影响显著，已严重制约农业可持续发展[1-4]。土壤压实的量化和评价是土壤结构保护与农业可持续管理的基础，而土壤压实模型（如SOCOMO模型）是量化和评估压实风险的有效工具，对制订农业机械田间作业通行性建议具有重要意义[5-6]。然而，土壤力学特性及其传递函数等输入参数的缺乏，阻碍了土壤压实模型在实际中的应用[7-8]。

土壤压缩特性常作为土壤压实模型的输入参数，用于农业机械田间作业的压实风险评估[8-9]。土壤压缩特性受水力学状态和土壤结构等因素的影响[10]。水力学状态常用含水率、基质势和水势来量化[11]。土壤结构包括易于量化的宏观土壤性质，如容重、孔隙比、比体积；也包括不易于量化的微观土壤微观结构，如土壤颗粒、团聚体[11]。此外，土壤压缩特性还受到土壤质地、有机质、加载时间和土样大小的影响[8,12]。

已有研究常用 Casagrande法和回归法拟合土壤压缩曲线得到土壤压缩特性，但是 Casagrande法拟合方法复杂，回归法拟合精度较低[13-14]。Gregory等[14]的研究表明，Gompertz函数能够准确拟合土壤压缩曲线，并计算得到高精度的土壤压缩特性。在已有的原状土压缩试验研究中，土壤压缩特性与土壤物理性质间的关系未有统一结论。Défossez等[15]的研究表明回弹指数和含水率之间没有相关性，而Lima等[9]得出回弹指数和含水率之间为二次多项式关系的结论；Défossez等[15]发现压缩指数和含水率呈负相关，而Imhoff等[12]发现压缩指数与含水率之间没有明显相关性，Lima等[9]发现压缩指数和含水率之间为二次多项式关系。Saffih-hdadi等[11]将彼此相互矛盾的试验结果归因于原状土不同的土壤质地、含水率和容重。因此，An等[10]和Saffi-hdadi等[11]使用重塑土进行土壤压缩试验，研究了土壤压缩特性与土壤物理性质（容重和含水率）之间的传递函数。但这些传递函数只适用于所研究的土壤类型，不具有通用性。

水稻土广泛分布于长江三角洲农业区，由于该地区高度农业机械化，农业生产深受土壤压实问题的困扰。因此，了解水稻土压缩特性随容重和含水率的变化，对农业机械作业时机的合理选择具有重要意义。目前，关于水稻土压缩特性及其与容重和含水率之间相关性的研究还很缺乏。在大尺度采集各地的土样进行压缩试验测定土壤压缩特性，需要耗费巨大的人力、物力和财力，因此建立模型是量化和评估土壤压实的有效手段。本文选取典型的水稻土为研究对象，采用Gompertz函数拟合土壤压缩数据，以研究含水率和容重对土壤压缩曲线和土壤压缩特性（回弹指数、压缩指数和先期固结压力）的影响，并建立土壤压缩特性与含水率和容重之间的函数关系。这些传递函数作为土壤压实模型的输入参数，可用于长江三角洲农业区农业机械田间作业的土壤压实量化和压实风险评估。

1 材料与方法

1.1 土壤样品制备

试验所需水稻土取自南京市六合区八百桥农场（118°59′E，31°98′N），水稻收获后取表层 0～20 cm 土壤带回实验室进行分析，土壤基本理化性质如表1所示。将取回的土壤进行风干，破碎，过 2 mm筛[13]，并去除2 mm以上的砂石（占土壤总质量的0.97%）。参照文献[16-17]的土样样品制备方法，以5%间隔制备含水率15%、20%、25%、30%、35%的重塑土，并密封于塑料箱中，静置24 h。试验用直径为50 mm的圆柱形样桶（高度为50 mm）制备容重为 1.1、1.2、1.3、1.4、1.5 g/cm3的土壤样品。制备土样前，沿样桶内壁均匀涂抹一层凡士林以减小土壤和样桶内壁之间的摩擦。每种参数的土壤样品重复3次，共制备75个土样。

表1 水稻土基本理化性质Table 1 Basic physicochemical properties of paddy soil

1.2 单轴压缩试验

使用固结仪对制备的土壤样品进行单轴压缩试验，如图1所示。按照25、50、100、200、400、800 kPa载荷次序添加砝码对土样进行压缩试验，每次加载间隔30 min，每次加载后用游标卡尺测量土壤下陷的位移[13]。

图1 土壤单轴压缩试验Fig.1 Uniaxial compression test of soil

根据土壤的下陷位移，计算不同载荷作用下土壤的孔隙比[18]

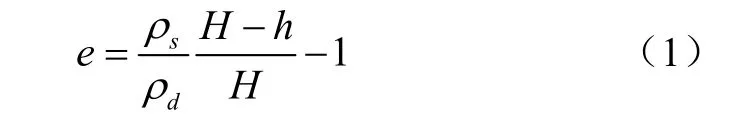
式中e为土壤孔隙比；ρs为土粒密度，g/cm3；ρd为土壤容重，g/cm3；H为土壤样品初始高度，cm；h为土壤下陷位移，cm。

1.3 土壤压缩特性计算

土壤压缩曲线可用两条近似直线表示：回弹线和原始压缩线[18]。从压缩曲线可以得到 3个重要的土壤压缩特性：回弹指数（Cs）、压缩指数（Cc）、先期固结压力（σPC）。

回弹指数CS为回弹线的斜率，其表达式为[14]

式中e0为初始孔隙比；e25为25 kPa加载力对应的孔隙比。

将由单轴压缩试验获取的孔隙比e代入Gompertz方程[10]

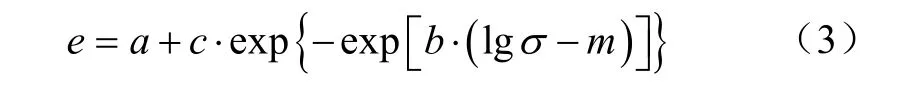
式中a、b、c、m为拟合系数；σ为压缩试验加载力，kPa。

压缩指数CC是原始压缩线的斜率，其计算公式为[14]

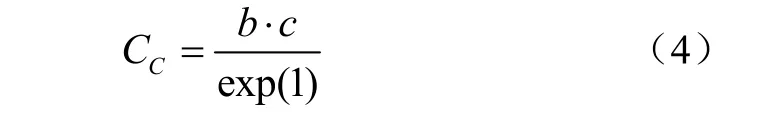
式（3）的一阶导数为压缩曲线拐点处的斜率，即压缩指数。由式（3）的二阶导数可得土壤压缩曲线的曲率k，计算公式如下[18]

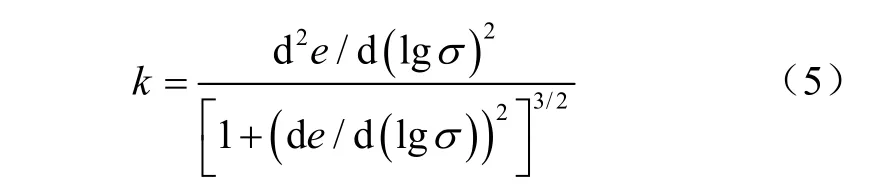
式（5）中最大曲率点对应的加载力，即为先期固结压力。

1.4 数据分析

采用SPSS19.0统计软件中的方差分析方法，研究含水率和容重对水稻土先期固结压力、压缩指数和回弹指数的影响，采用LSD方法进行多重比较，对显著性差异进行统计学分析。

2 结果与分析

通过式（2）、（4）和（5）计算得到不同含水率和容重下的回弹指数、压缩指数和先期固结压力，采用Excel2010绘图，得到图3、4和5。

2.1 土壤压缩曲线拟合

由单轴压缩数据点拟合得到不同容重下，含水率对水稻土压缩曲线的影响，如图 2所示。不同含水率和容重下的水稻土压缩曲线形状基本一致。当加载力小于25 kPa时，压缩曲线近似直线，即回弹线，水稻土为弹性变形；当加载力处于25～200 kPa之间时，压缩曲线出现明显拐点；当加载力大于200 kPa时，压缩曲线近似为直线，即原始压缩线，水稻土为塑性变形。这与An等[10-11]试验结果相吻合。这一结果可用土壤应力应变理论解释，当加载力小于土壤强度时，土壤变形近似直线，为弹性变形；当加载力超过土壤强度时，近似直线的土壤变形出现拐点；当加载力继续增大时，土壤变形又近似直线，为塑性变形[18]。如图 2所示，当含水率相同时，随着容重的增大，土壤孔隙比减小量（Δe）变小，即水稻土形变量（Δh）变小，这一结果与已有研究结论相符[10-12,19]。这一结果表明，对于相同的加载力，土壤容重越大，即土壤颗粒排列越紧密，土壤形变量越小，土壤越不容易压实。容重相同时，当含水率为15%～25%时，随着含水率的增大，Δe变大，即Δh增大；当含水率为25%～35%时，随着含水率的增大，Δe变小，即Δh减小。这与Lima等[9]的试验结果相吻合，表明对于相同加载力，随着土壤含水率增大，Δh先增大后减小。当含水率为25%时，Δh达到最大，因此也最容易压实。

Gompertz函数（式（3））与不同容重和含水率下的压缩试验数据拟合较好，决定系数在0.991～0.999之间，平均值为0.998；均方根误差（RMSE）范围在0.001～0.019之间，平均值为 0.008。式（3）中各拟合系数范围为a=0.289～0.643，b=0.980～2.883，c=0.128～1.087，m=2.157～2.598。由图2可知，当式（3）中加载力（σ）为零时，土壤孔隙比取得最大值，即emax=e0=a+c。由图2可知，随着加载力（σ）的增大，土壤孔隙比逐渐减小。当式（3）中加载力（σ）趋于无穷时，土壤孔隙比取得最小值，即emin=a。

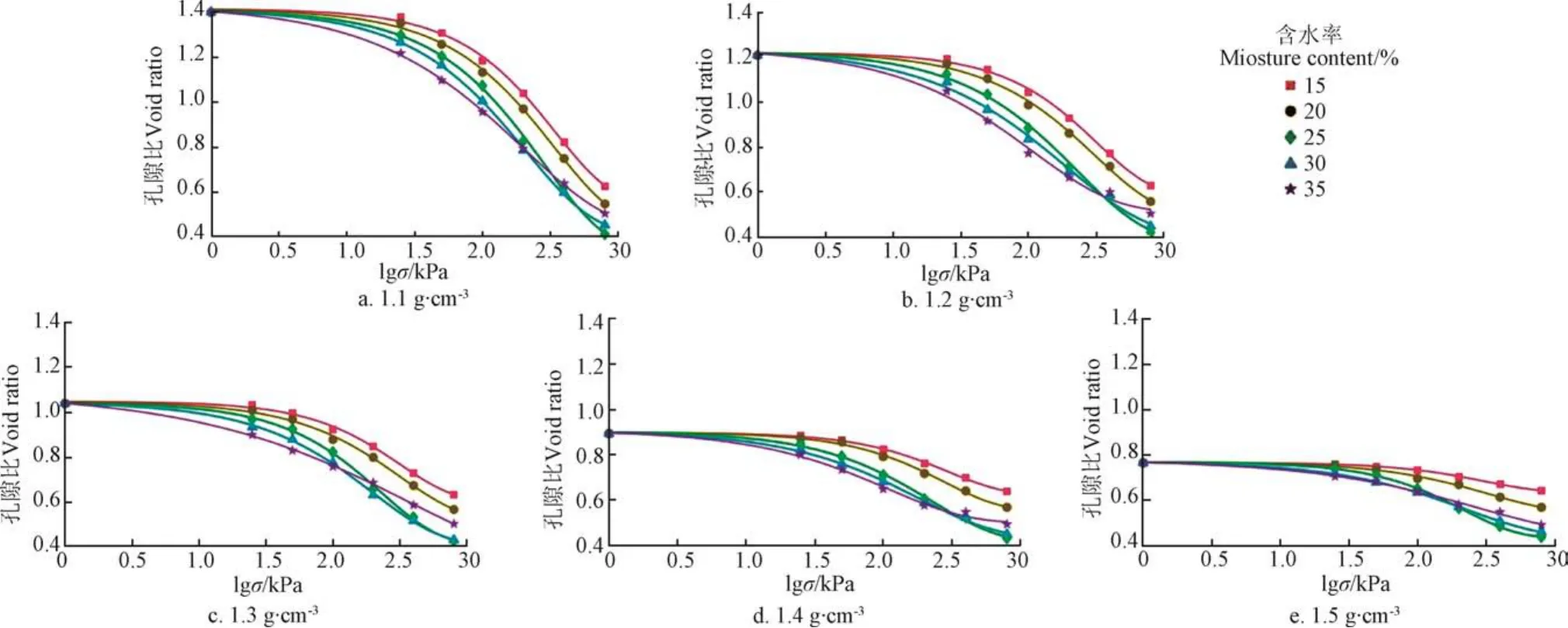
图2 不同容重下含水率对水稻土压缩曲线的影响Fig.2 Effects of moisture content on compression curves of paddy soil under different bulk densities

2.2 含水率和容重对回弹指数的影响

回弹指数是衡量土壤回弹和自我恢复的能力的一项重要指标，回弹指数越大，土壤的恢复力越强[18,20]。由图3可知，土壤含水率和容重对回弹指数影响显著（P＜0.05）。在含水率为15%，容重为1.5 g/cm3时，回弹指数最小；在含水率为35%，容重为1.1 g/cm3时，回弹指数最大；回弹指数为0.003～0.138。容重一定时，含水率越大回弹指数越大，含水率一定时，容重越大回弹指数越小，表明水稻土压实后的恢复能力随含水率增大而增大，随容重增大而减小。

图3 含水率和容重对水稻土回弹指数的影响Fig.3 Effects of moisture content and bulk density on swelling index of paddy soil

对含水率和容重与回弹指数之间的关系进行回归分析，当含水率和回弹指数以及容重和回弹指数为线性函数时，其决定系数最高（如表 2所示）。回弹指数与含水率和容重之间的函数方程为

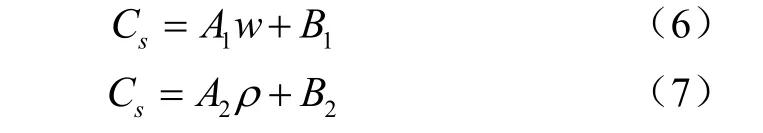
式中A1、A2为拟合系数；w为含水率，%；ρ为容重，g/cm3；B1为w=0时，水稻土的理论回弹指数；B2为ρ=0时，水稻土的理论回弹指数。

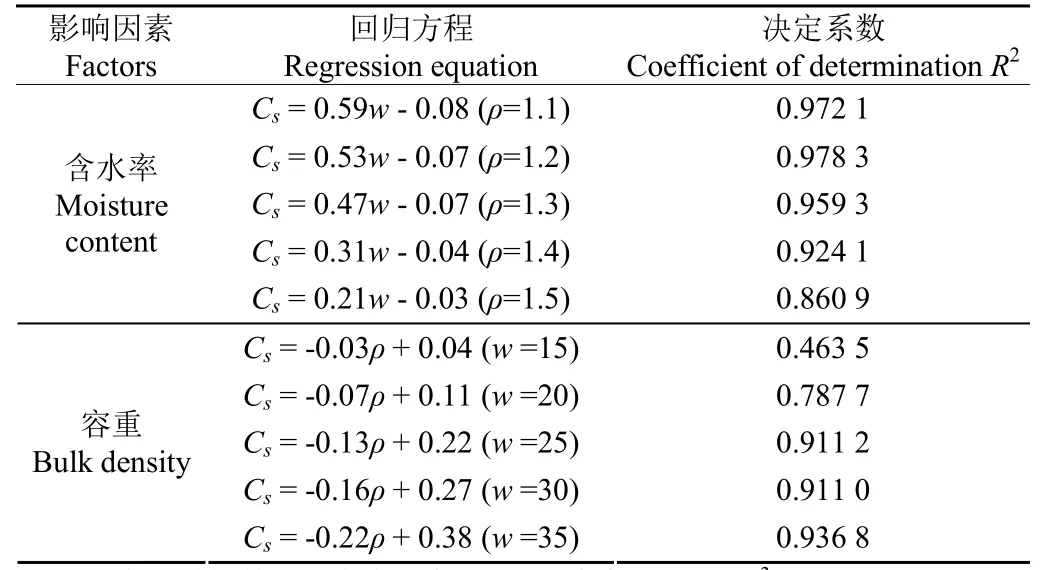
表2 水稻土回弹指数与含水率和容重的线性回归分析Table 2 Linear regression analysis for swelling index and moisture content or swelling index and bulk density of paddy soil

2.3 含水率和容重对压缩指数的影响

压缩指数是反映土壤压实敏感性和抗压能力的一项重要指标[12]。压缩指数越大，土壤压实敏感性越强，即抗压实能力越弱；反之，抗压实能力越强。由图4可知，含水率和容重对水稻土压缩指数影响显著（P＜0.05）。在含水率为15%，容重为1.5 g/cm3时，压缩指数最小；在含水率为25%，容重为1.1 g/cm3时，压缩指数最大；压缩指数在 0.115～0.839之间。容重一定时，水稻土压缩指数随含水率的增大，呈先增大后减小趋势，且在含水率为25%时取得最大值。这表明含水率为25%时，水稻土对压实最敏感，抗压实能力最弱，最容易受到压实。含水率一定时，水稻土压缩指数随容重的增大而减小，这表明水稻土在较大容重时对压实不敏感，抗压实能力强。因此，当含水率为 25%附近时，应避免农业机械的田间作业。同时，也应避免在土壤容重较低（如刚耕后的土壤）时的田间作业。

对含水率和容重与压缩指数之间的关系进行回归分析，当含水率和压缩指数为二次多项式函数时，其决定系数最高，容重和压缩指数为线性函数时，其决定系数最高（如表 3所示）。压缩指数与含水率和容重之间的函数方程分别为

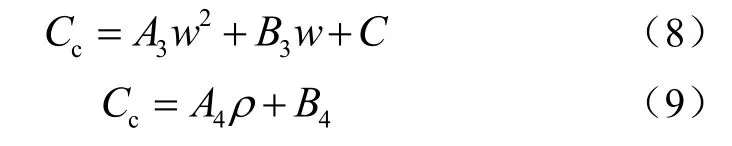
式中A3、A4、B3为拟合系数；B4为ρ=0时，水稻土的理论压缩指数；C为w=0时，水稻土的理论压缩指数。

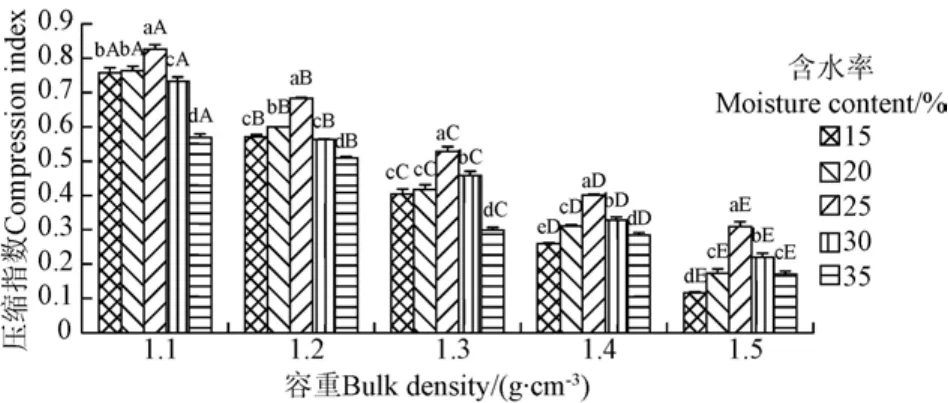
图4 含水率和容重对水稻土压缩指数的影响Fig.4 Effects of moisture content and bulk density on compression index of paddy soil

表3 水稻土压缩指数与含水率和容重的回归分析Table 3 Regression analysis for the relation between compression index and moisture content or compression index and bulk density of paddy soil

2.4 含水率和容重对先期固结压力的影响

先期固结压力是衡量土壤的压缩强度和承载能力的一项重要指标[21]。先期固结压力越大，土壤承载力越大；反之，土壤承载力越小[22]。从图 5可以看出，土壤含水率和容重均对先期固结压力影响显著（P＜0.05）。先期固结压力在含水率为35%，容重为1.1 g/cm3时取得最小值；在含水率为15%，容重为1.5 g/cm3时取得最大值；先期固结压力为 33～127 kPa。容重一定时，先期固结压力随含水率的增大而减小；含水率一定时，先期固结压力随容重增大而增大。这表明水稻土承载力随着含水率的增大而减小，随着容重的增大而增大。因此，应该防止农业机械在较高的含水率和较低的容重情况下的田间作业。

对含水率和容重与先期固结压力的关系进行回归分析，当含水率和先期固结压力以及容重和先期固结压力为线性函数时，其决定系数最高（如表 4所示）。先期固结压力与含水率和容重之间的函数方程为

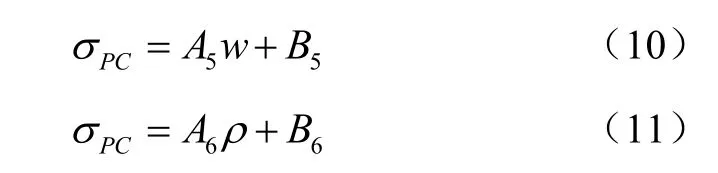
式中A5、A6为拟合系数；B5为w=0时，水稻土的理论先期固结压力；B6为ρ=0时，水稻土的理论先期固结压力。

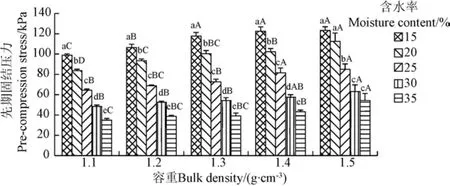
图5 含水率和容重对水稻土先期固结压力的影响Fig.5 Effects of moisture content and bulk density on pre-compression stress of paddy soil

表4 水稻土先期固结压力与含水率和容重的线性回归分析Table 4 Linear regression analysis for pre-compression stress and moisture content or pre-compression stress and bulk density of paddy soil

3 讨 论

3.1 回弹指数

Lima等[9]发现巴西2种氧化土的回弹指数为0.01～0.02。Keller等[18]发现瑞典4个农场的回弹指数为0.002～0.025。O’Sullivan等[23]发现英国砂质壤土和黏质壤土的回弹指数为 0.0002～0.012 8。Défossez等[15]发现法国黄土和石灰性土的回弹指数是一个固定值，为 0.005 8。这些结果均小于本文所测水稻土的回弹指数（0.003～0.138）。

对于不同土壤中回弹指数差异的原因，以往的研究常从土壤黏粒含量和有机碳含量 2个方面解释。Stone等[24]对5种土壤的研究发现，黏粒含量越低，回弹指数越小。Lima等[9]也将2种氧化土较小的回弹指数归因于较低的黏粒含量。已有研究表明，回弹指数随着有机碳含量（SOC）的增加而增加。Braida等[25]发现巴西土壤中的回弹指数范围在0.002（5 g/kg SOC）到0.01（25 g/kg SOC）之间，与 Capurro等[26]的研究结果相吻合。Pereira等[27]研究显示回弹指数范围在0.005（8 g/kg SOC）到0.015（25 g/kg SOC）之间。Lima等[9]研究表明氧化土中的回弹指数范围在0.01（30 g/kg SOC）到0.02（40 g/kg SOC）之间。

水稻土的黏粒含量（260 g/kg）介于2种氧化土黏粒含量（220和320 g/kg）之间，但水稻土回弹指数却明显大于 2种氧化土的回弹指数。水稻土的有机碳含量（13 g/kg）介于这些研究的有机碳含量之间，但是水稻土的回弹指数是最大的。因此，不同土壤中回弹指数的差异除了与黏粒含量、有机碳含量有关，还与土壤强度有关。Keller等[18]利用压缩过程中储存的弹性能来解释这一现象，即土壤强度越大，存储的弹性能越小。重塑土的强度要小于田间结构土的强度，因此重塑土的回弹指数要大于结构土的回弹指数。

Défossez等[15]对石灰性土和黄土的研究发现回弹指数是一个固定值，不会随含水率的变化而变化。这是因为土壤结构的空间变异性会很大程度上影响试验结果。本文采用重塑水稻土降低了土壤结构的空间变异性，发现回弹指数与含水率呈线性正相关，与容重呈线性负相关。

3.2 压缩指数

An等[10]研究表明重塑黑土的压缩指数在 0.293～0.950之间，重塑棕壤土的压缩指数在0.980～2.065之间。本文水稻土压缩指数在 0.115～0.839之间，远小于棕壤土压缩指数，但与黑土压缩指数很相近，且与大多数的研究结果相一致[12,14,23]。

压缩指数与含水率之间的关系在不同的研究中未有统一结论。Saffih-hdadi等[11,15,28-29]研究发现压缩指数和含水率呈负相关。An等[10]试验结果表明，在黑土中压缩指数和含水率呈正相关，在棕壤土中则没有相关性。Larson等[30]研究也发现压缩指数与含水率之间没有明显相关性。根据本文的研究结果，分析出现以上 3种不同试验结果的原因。水稻土压缩指数最大值对应的含水率为25%，近似等于土壤塑限（wPL）。当含水率小于土壤塑限时，土壤压缩指数与含水率呈正相关；当含水率大于土壤塑限时，土壤压缩指数与含水率呈负相关；当土壤塑限介于所研究含水率区间时，土壤压缩指数与含水率相关性不明显。因此，土壤压缩指数与含水率之间的相关性受到土壤塑限的影响。

水稻土容重和压缩指数呈负相关关系，这一结果与已有研究结论相一致[8,10-12,22,31]。Saffih-hdadi等[11]研究表明压缩指数与容重相关，且随着容重的增大而减小。Tang等[31]研究也发现土壤在较低的容重下更容易压缩。这是因为土壤容重较大时，土壤颗粒排列更紧密，供颗粒移动的孔隙空间更小，颗粒之间的摩擦力更高。因此，随着容重的增加，土壤变形变得更加困难[32]。

3.3 先期固结压力

水稻土的先期固结压力与含水率呈负相关，这与An等[10,12,33-34]研究结果一致。这些研究认为，二者之间的负相关关系是因为土壤孔隙中的水分体积和土壤颗粒周围水膜厚度会随着含水率的增加而增加，这减小了颗粒间的弯月面力，降低了有效应力[10]。随着弯月面的减少，颗粒间接触点的数量也相应减少[12]。水稻土的先期固结压力与容重呈正相关，这一结果与大多数研究结论一致[11,22,29,34]。这些研究人员都将这种效应解释为颗粒间摩擦力的增加，并将通过阻碍土壤颗粒的分离和移动来增加土壤的承载能力[12]。先期固结压力与含水率和容重之间的相关系数高于许多先前的研究。这与本文所用的重塑土和试验条件有关。Peng等[35]研究发现重塑土减小了土壤结构变异性的影响。

综上分析，本文基于大范围的土壤含水率和容重取值建立的水稻土传递函数，能够较好地估计水稻土的先期固结压力。在实际生产中，通过土壤含水率和容重两个容易获取的土壤参数预测土壤承载力，并将田间机械作业的接地压力限制在土壤承载力之下，土壤压实风险会大大降低。

4 结 论

Gompertz函数对水稻土试验数据的拟合效果较优，决定系数为0.991～0.999。测量了较大范围水稻土初始条件下的回弹指数、压缩指数分别为0.003～0.138、0.115～0.839，先期固结压力为33～127 kPa。建立了水稻土压缩性质与容重和含水率之间的传递函数：即回弹指数和压缩指数与容重呈线性负相关，先期固结压力与容重呈线性正相关，回弹指数与含水率呈正相关，压缩指数与含水率呈二次多项式关系，先期固结压力与含水率呈负相关。压缩指数在含水率为 25%时取得最大值，即在土壤塑限处水稻土压实风险最大。因此，为了减小土壤压实发生的风险，应该避免农业机械在 25%含水率附近、较高含水率时和较低容重时的田间作业。

本文建立的水稻土压缩性质与容重和含水率之间的传递函数，不但可用于长江三角洲农业区水稻土压缩特性的预测，避免了费时费力的土壤压缩试验，而且对农业机械田间作业合理时机的选择具有重要意义。同时，这些传递函数可作为土壤压实模型的输入参数，用于长江三角洲农业区农业机械田间作业压实破坏的量化和压实风险的评估。