马铃薯播种机播深调控装置设计与试验

吕金庆，杨晓涵，冯 雪，李紫辉，李季成，刘中原

（东北农业大学工程学院，哈尔滨 150030）

0 引 言

马铃薯在中国种植面积广泛，现已与玉米、水稻、小麦共同被列入四大主粮作物[1-2]。马铃薯机械化播种对于产量有着很大的影响，在播种时，由于土壤阻力的不同和地形起伏的变化，再加上地表有大量的残茬和茎秆覆盖等原因，播种单体在播种过程中的播深稳定性受到严重的影响，进而影响播种质量和出苗率。播深一致性的好坏决定着出苗率、出苗整齐度、幼苗状况及随后的生长发育，最终决定产量[3-5]。

在播种单体上设置合理的仿形机构，对解决马铃薯播种过程中的播种深度不一致问题，有极其重大的意义。仿形机构作为在播种过程中影响开沟器入土深度的关键部件，其工作性能的优劣将直接影响播种质量[6-8]。国内马铃薯播种机主要依靠地轮整体仿形，单体仿形机构应用较少，播深一致性较差。近年来对马铃薯播种机仿形播种单体的研究已逐渐增多，吕金庆等[9]设计了一种2CMQ2型气吸式马铃薯播种机，该马铃薯播种机具备独立的播种单体，可一次性完成开沟、施肥、播种、覆土等多项作业，具有作业效率高、作业质量好、排肥量大、调节方便、运行可靠、稳定性高的特点，提高了作业效率和播种精度；德沃公司研制的 2CMZ-4型马铃薯播种机，采用独立播种单体结构，可根据不同的种植模式调节垄距和株距，以适应不同地域需求[10]。国外马铃薯播种机大量采用自动化控制、液压系统供种、播种电子监测等先进技术，智能化和精量化程度较高。格力莫公司生产的Grimme430型马铃薯种植机[11]，可以在土地上非常精确和均匀地播种，平行四边形犁铧开沟器由 4个直径为400 mm的仿形轮推动，播深一致性较好；Grimme GL34T型马铃薯播种机，播种和施肥同时进行且十分精确，并且通过丝杠长短调节限深轮限制播深，保证播种深度的一致性[12]；美国DoubleL公司生产的9540型马铃薯播种机，驾驶员可以在驾驶室中电子控制播种间距，操作方便，运用仿形机构来满足地形变化时的播种要求，作业效率和精度较高[13]。国外马铃薯播种机在大型多行（4行以上）多采用单体仿形调节播种单体的播种深度，满足多行宽幅马铃薯播种质量的要求，但国外马铃薯的种植土壤条件、降水气候等均与国内存在明显差异，且国外马铃薯种植机械的价格昂贵，配件供应不及时，不符合中国国情，难以在中国马铃薯产区推广应用。

因此，展开适用于多行宽幅大型马铃薯播种机和丘陵山地小型马铃薯播种机仿形单体的研究，对于解决马铃薯播深不一致性等问题具有重要意义。针对上述问题，研制一种新型马铃薯播深调控装置，通过对播深调控装置的理论分析，确定影响播深一致性的关键因素。采用旋转正交的试验方法进行田间试验，得出该播深调控装置作业效果的最优参数组合，并验证所设计的播深调控装置效果是否满足马铃薯田间精量种植的要求。

1 播深调控装置的结构及工作原理

如图 1所示，播深调控装置主要由平行四杆仿形机构、限深轮和开沟器 3部分组成。限深轮的安装位置不同，对仿形效果的影响也不同，可以根据机具的结构和具体尺寸决定限深轮的配置。其中，平行四杆仿形机构的上拉杆与下拉杆平行且相等，上拉杆、下拉杆和后支架构成的连杆系统绕两铰接点转动，由平行四边形的运动特点可知，在上下仿形过程中，上拉杆和下拉杆始终做平行运动，从而使刚性连接在后支架上的开沟器在作业过程中的入土角度恒定不变，当地势较低时，压力弹簧会对上下拉杆有一个压力作用，防止开沟器开沟深度过浅，平行四杆仿形机构同时与仿形限深轮共同作用，保证开沟器在地势起伏情况下开出深浅一致的种沟，为种薯出苗的一致性和作物生长的整齐性提供了条件。

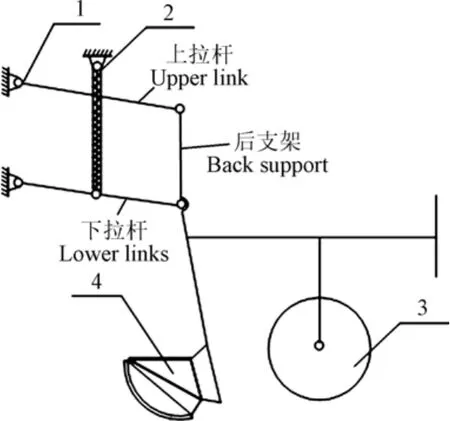
图1 播深调控装置结构示意图Fig.1 Schematic diagram of sowing depth control device

2 播深调控装置的结构设计

2.1 平行四杆仿形机构的设计

2.1.1 弹簧刚度的设计

播种单体工作时的受力如图2所示。

由平衡条件可得

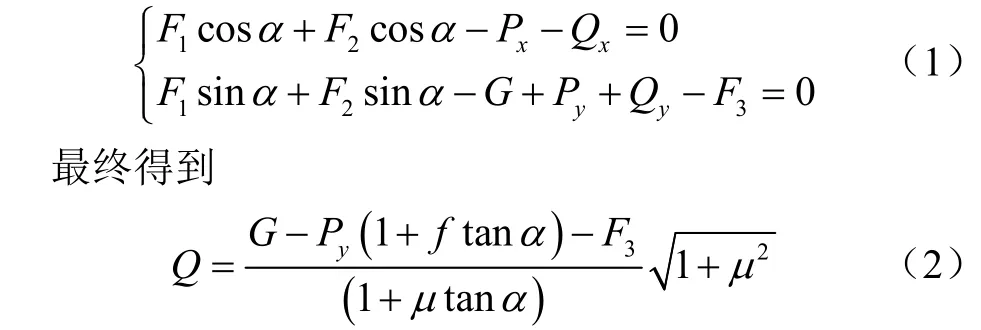
要使开沟器稳定工作，则要求仿形限深轮上有适当的垂直反力。如果垂直反力过小，则说明播种单体质量轻，开沟器入土能力差导致开沟深度不稳定；如果垂直反力过大，则使限深轮陷入土壤太深，增加滚动阻力。为保证开沟深度稳定，工作时应保证Q＞0。由式可得出播种单体质量最小值应满足

式中Δl为弹簧变形量，mm；L为平行四杆上下拉杆的长度，mm。

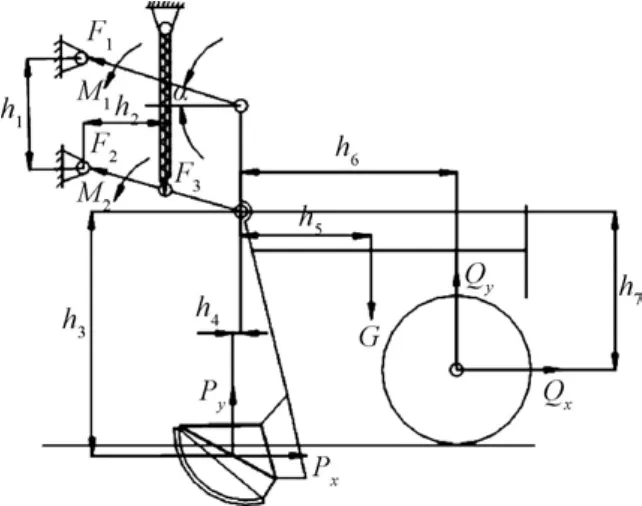
图2 播种单体受力分析图Fig.2 Seeding unit stress analysis chart

安装弹簧时，要保证在一般播深情况下有一定的预压力。如果预压力过小，下仿形时可能出现入土力矩不够，导致开沟深度过浅。因此，弹簧预压力应能保证下仿形量最大时仿形限深轮垂直反力Q＞0。假设下仿形量最大时播种机的牵引角为α，则由式（3）可得

由上式可见，弹簧刚度系数受到开沟器工作阻力、播种单体所受重力、四杆机构尺寸的影响。为了保证播种机在下仿形时能工作可靠，选择弹簧时，弹簧刚度系数应大于某一值。但弹簧刚度系数过大会导致预压力过大，下仿形时会导致开沟器开沟深度变深，因此，在保证预压力足够的前提下应该选用弹簧刚度系数较小的弹簧。

2.1.2 平行四杆仿形尺寸的设计

影响平行四杆仿形能力的直接因素就是其合理的结构参数，因此，为了保证开沟器在随地面轮廓上下起伏的过程中稳定工作，确定各杆件的尺寸是非常重要的。

1）牵引角α的设计

因播种机仿形机构仿形量的大小与对土地的处理程度和地形有关，所以，各杆尺寸的大小需要按照实际的播种农艺要求及仿形量来决定。一般情况下，上下仿形量各为80～120 mm；若要使上下仿形量相同，上下拉杆越短，则牵引角 α变化范围越大；平行四杆的上下拉杆越长，则牵引角 α变化范围越小。为了保证播种单体在作业过程中的稳定性，则牵引角的取值小一些有利。所以，下拉杆的尺寸越长越有利于提高播种机具的稳定性。但拉杆长度过长，使结构不紧凑，机具重心后移[14-16]，上下仿形的尺寸参数如图3所示。

总仿形量为

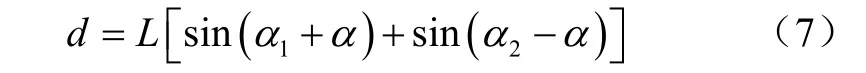
一般播种机上，牵引角α的取值范围为0～10°，下仿形牵引角α2的取值范围为6°～22°，此即播种深度为最深时的变化范围，上仿形总量α+α1变化范围为20°～40°，此即播种深度为最浅的变化范围。依据农业设计手册[17]，α1=15°，α=0，α2=15°。

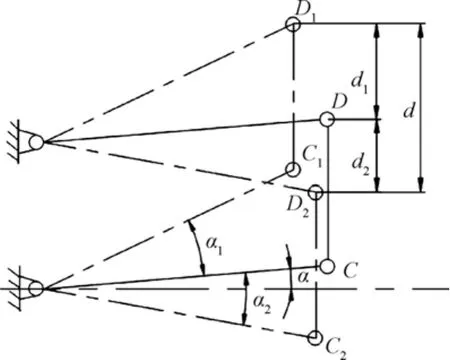
图3 仿形极限位置示意图Fig.3 Schematic diagram of extreme position of profiling mechanism

2）杆长L的设计

假定 α=0°，同时其上下移动的量相同，因此，只须确定任何一边的尺寸即可，由图3可知

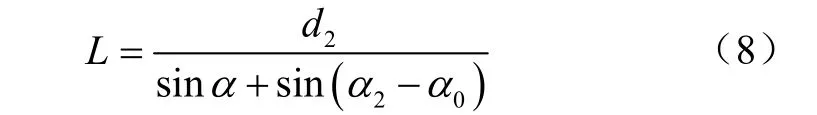
式中d2为下仿形的尺寸，选择其值为100 mm；α0为初始的工作角度，取其值0；α2为下仿形角度，取其值15°，将已知代入式得L=386 mm，取L=400 mm，则可以得到上仿形量

式中α1为上仿形角，取15°。将已知代入式，d1=104 mm，满足仿形量80～120 mm的要求。

2.2 仿形限深轮的配置

为了使开沟器更加准确地贴合地表形状，使开沟深度随着地面的起伏而达到播深一致性，需要利用仿形限深轮与平行四杆仿形机构共同配合使用[18-20]。平行四杆仿形机构可以保证开沟器恒定的入土角度，使开沟器相对于初始位置上下浮动仿形；仿形限深轮与地面滚动接触实时跟随地表起伏，保证其与开沟器之间的竖直距离恒定不变，进而决定开沟深度的变化[21-22]。

假设播种机作业时遇到正弦曲线变化的地表形状，设初始播种深度p（mm），地面起伏最大高度h（mm），地面起伏的水平长度B（m），开沟器与仿形轮间的距离b（mm），仿形轮在前，b为负值，仿形轮在后，b为正值。

则地面曲线可表示为

对播深求导得

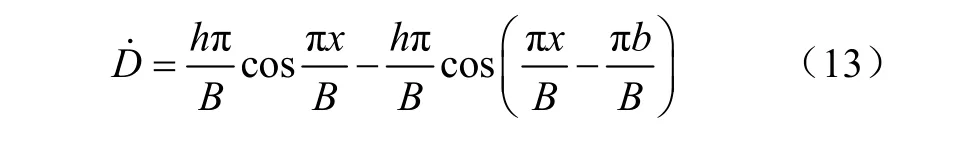
由式（13）可知，当b=0时，播深的导数恒为0，即播种深度保持不变。所以，仿形限深轮的位置应在不堵塞、壅土的条件下与开沟器的距离尽量小一些。本研究结合机具的具体结构尺寸，将仿形轮安装在开沟器前方30 cm处。

2.3 开沟器的设计

马铃薯播种时开沟深度较深，参照传统滑刀式开沟器，本文采用开沟器主体与开沟器铲片组合的形式，开沟器主体与开沟器铲片通过沉头螺栓进行固定连接，可根据不同的作业要求调整安装孔的位置；根据马铃薯的播种农艺要求，在播种时最大耕深可达到150 mm[23]，设计开沟器铲片高度为160 mm，略大于开沟深度；马铃薯需要播种时种沟宽度较大，一般不小于150 mm[24-25]，参照铧靴式马铃薯开沟器尺寸，同时综合考虑开沟器安装位置、排种器宽度和垄台宽度，设计开沟器的宽度为280 mm[26]；为保证前铲片对土壤的滑切作用，倾角应大于 90°+φ，其中 φ为土壤与铲片间的摩擦角，一般 φ在15°～38°之间，设计的铲片入土角为 135°[27]；参照传统滑刀式开沟器，综合考虑开沟器的作业强度及作业效果，设计的铲片厚度为8 mm；为保证下层土壤颗粒可先落到沟中覆盖马铃薯种子，利于马铃薯发芽，设计开沟器主体侧板底部为向内倾斜45°的形式；为了减小工作阻力，应尽量减小开沟器铲片的夹角，理论上其夹角不应超过90°，设计开沟器铲面夹角为 60°。开沟器的整体长度为500 mm，其结构如图4所示。

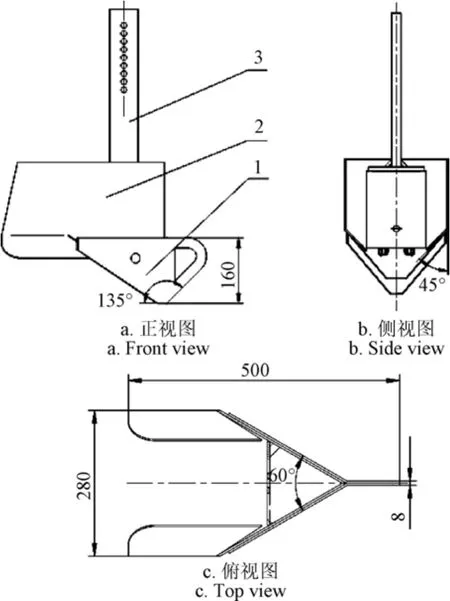
图4 滑刀式开沟器三视图Fig.4 Three view of sliding-knife opener

3 播种单体开沟深度稳定性模型

假设播种机以速度 v0匀速运动，正常工作时的牵引角为 α0，此时开沟器在某一稳定开沟深度工作，播种单体重心坐标为A1(x0,y0)。如果工作部件受到扰动力矩的作用使开沟深度变浅，牵引角向上摆动量为β，则单体重心移动到A2(x1,y1)的位置。如图5所示。

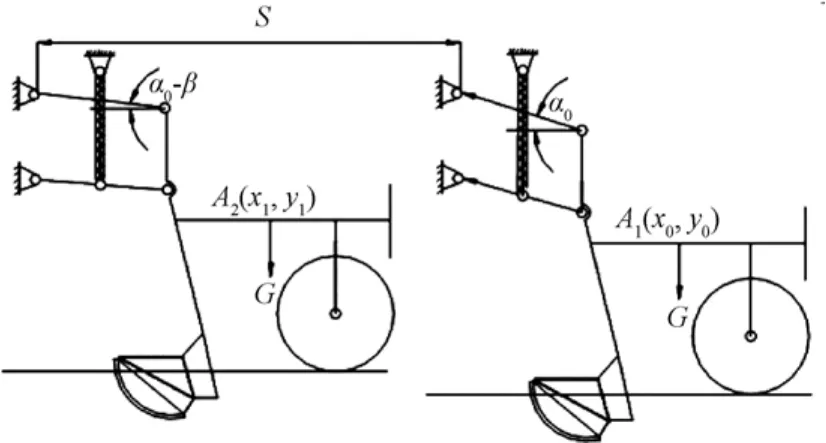
图5 仿形过程示意图Fig.5 Schematic diagram of profiling process

由图5的几何关系可知

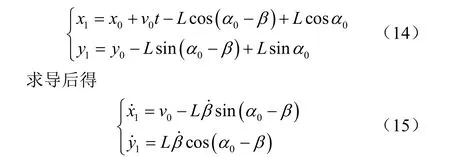
把牵引角向上摆动量 β作为广义坐标，根据拉格朗日第二方程建立开沟器运动的微分方程

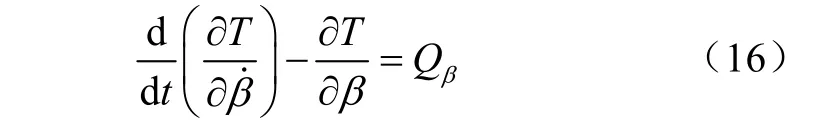
式中T为系统动能，J；Qβ为广义力，N。

该系统的动能为

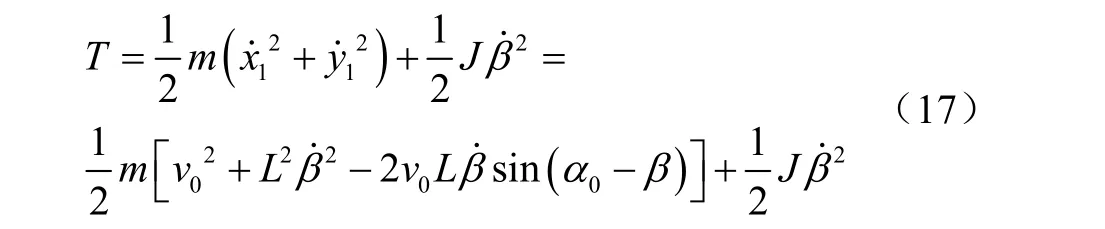
式中m为系统质量，kg；J为系统对垂直于纸面通过重心轴线的转动惯量，kg/m2。

由虚功方程式可知，广义力等于扰动力矩，可得

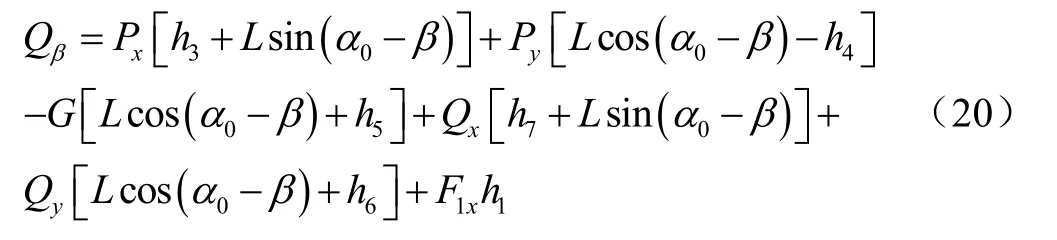
由于作用于平行四杆机构上下拉杆前铰接点的拉力的水平分力比较接近，所以可近似认为

式中F1x为播种机工作时拖拉机牵引力作用在平行四杆仿形机构上拉杆的力F1的水平分力，N；F2x为播种机工作时拖拉机牵引力作用在平行四杆仿形机构下拉杆的力 F2的水平分力，N

由力的平衡条件可得

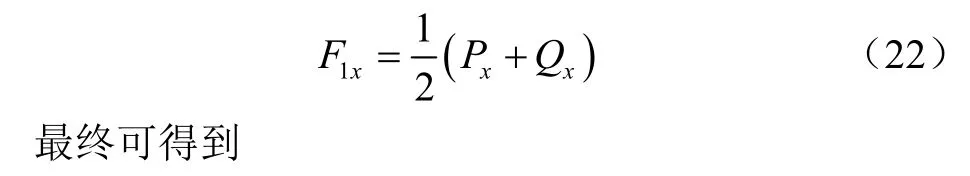
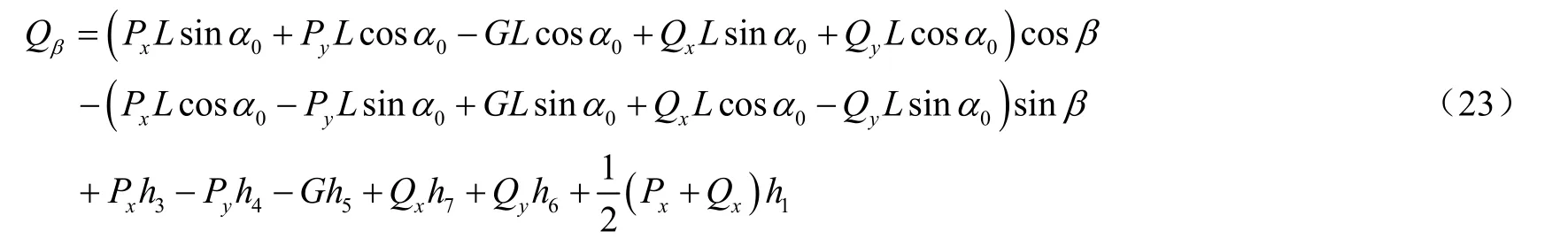
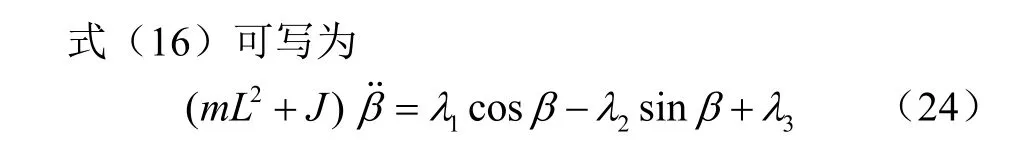
式中 λ1、λ2为系数；λ3为常数项。

积分后得

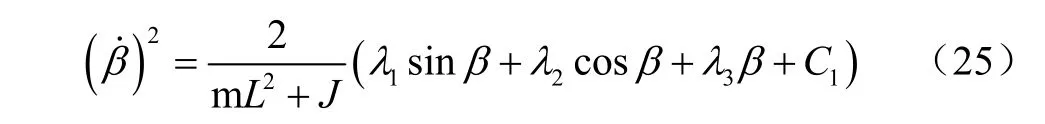
当牵引角为α0，开沟器在某一稳定开沟深度工作时，β=0，0，所以可求得积分还原常数 C1=-λ2，在 β角很小的情况下，可以近似取sinβ≈βcosβ ≈ 1 - ，则

由积分初始条件可得积分还原常数C2=0。

因此，最终播种机开沟深度稳定性数学模型为

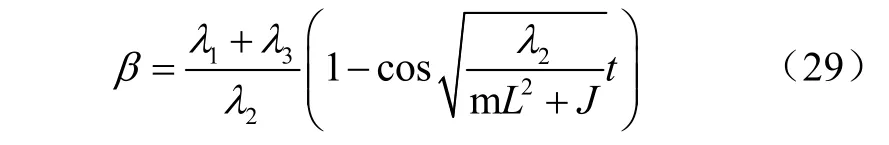
式中t为为播种单体仿形时牵引角向上摆动的时间，s。

该模型反映了播种单体的结构参数及作用在系统上的力与开沟器在垂直平面内对原始位置偏斜程度的关系。由式（29）可知，初始牵引角 α0的大小直接影响播种单体仿形时牵引角向上的摆动量β，进而影响开沟深度的一致性。同时，机构的质量与尺寸的配置、弹簧的力学性能等对开沟深度的稳定性也具有一定的影响。

4 田间试验

4.1 试验条件

2019年5月在黑龙江省农业科学研究院试验基地，进行田间试验。土壤为普通黑土，土壤坚实度为74 kPa，土壤含水率为17.0%；播种机的配套动力为59.6 kW的拖拉机；田间作业及测量过程如图6所示。

图6 田间试验Fig.6 Field experiment

4.2 评价指标

参照《GB/T 6242-2006 种植机械马铃薯种植机 试验方法》规定的试验方法[28]，考察马铃薯播种机播深调控装置的工作性能。以初始牵引角、弹簧钢度、机具作业速度为试验因素，开沟深度合格指数、开沟深度变异系数为试验指标，进行二次正交旋转组合试验，每组试验重复3次，计算测量结果的平均值。

选择开沟深度合格指数及开沟深度变异系数为评价指标，测量方法如下：

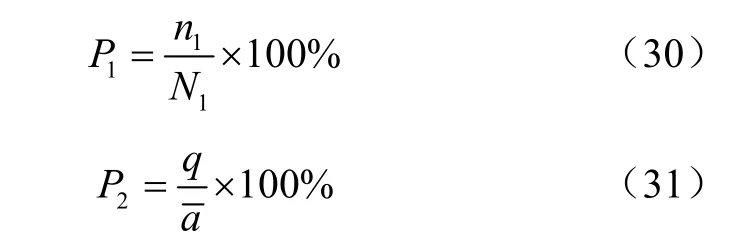
式中P1为开沟深度合格指数；n1为开沟深度合格数量；N1为开沟深度测定总数量；P2为开沟深度变异系数：q为开沟深度标准差，mm；为平均开沟深度，mm。

4.3 试验方案与结果分析

4.3.1 二次旋转正交组合设计试验

进行（三因素）二次旋转正交组合试验，以初始牵引角、弹簧钢度、机具作业速度为试验因素，各因素的水平范围为：初始牵引角−10°～10°，弹簧钢度 5～15 N/mm，播种机的作业速度0.5～1.5 m/s。进行田间试验的过程中，可根据不同的实际情况对播种机进行调节。通过试验，对开沟深度合格指数、开沟深度变异系数进行显著性的分析，根据实际需要对各个参数组合进行优化[29-30]，试验因素水平编码表如表 1所示，试验方案及试验结果如表2所示。

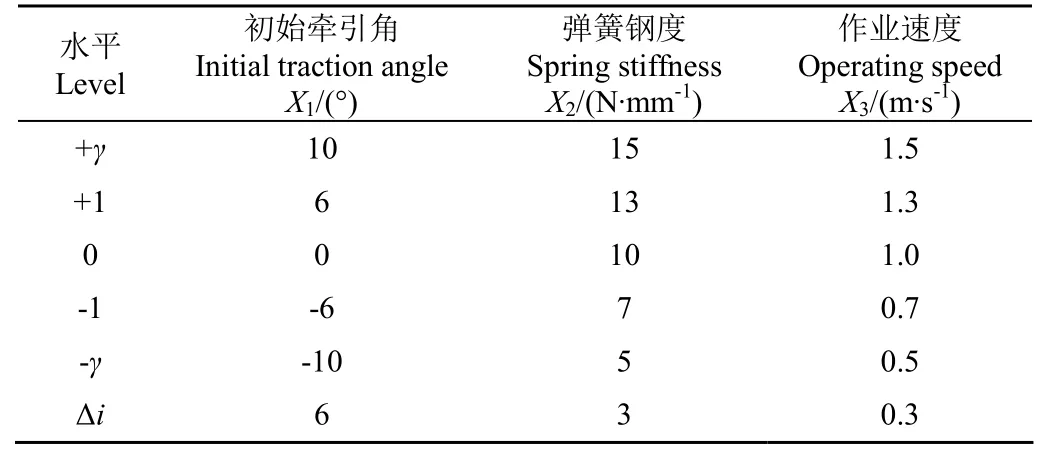
表1 试验因素及水平Table 1 Experimental factors and levels

4.3.2 试验结果分析与回归模型建立

利用Design Expert 8.0.6软件对试验结果进行二次回归分析，并进行多元回归拟合，得到开沟深度合格指数Y1、开沟深度变异系数Y2，2个试验指标的回归方程，并检验其显著性。

1）开沟深度合格指数Y1的显著性分析

通过对数据的分析，开沟深度合格指数Y1方差分析如表3所示。由表3可知，试验模型显著（P＜0.01），主因素中初始牵引角、弹簧刚度、作业速度对指标影响均极显著，交互项中弹簧刚度和作业速度的交互作用X2X3对指标影响最大，为极显著。将不显著因素并入残差项后再次进行方差分析，结果如表 3所示，得到各个因素与指标间的回归方程如式（32）所示。

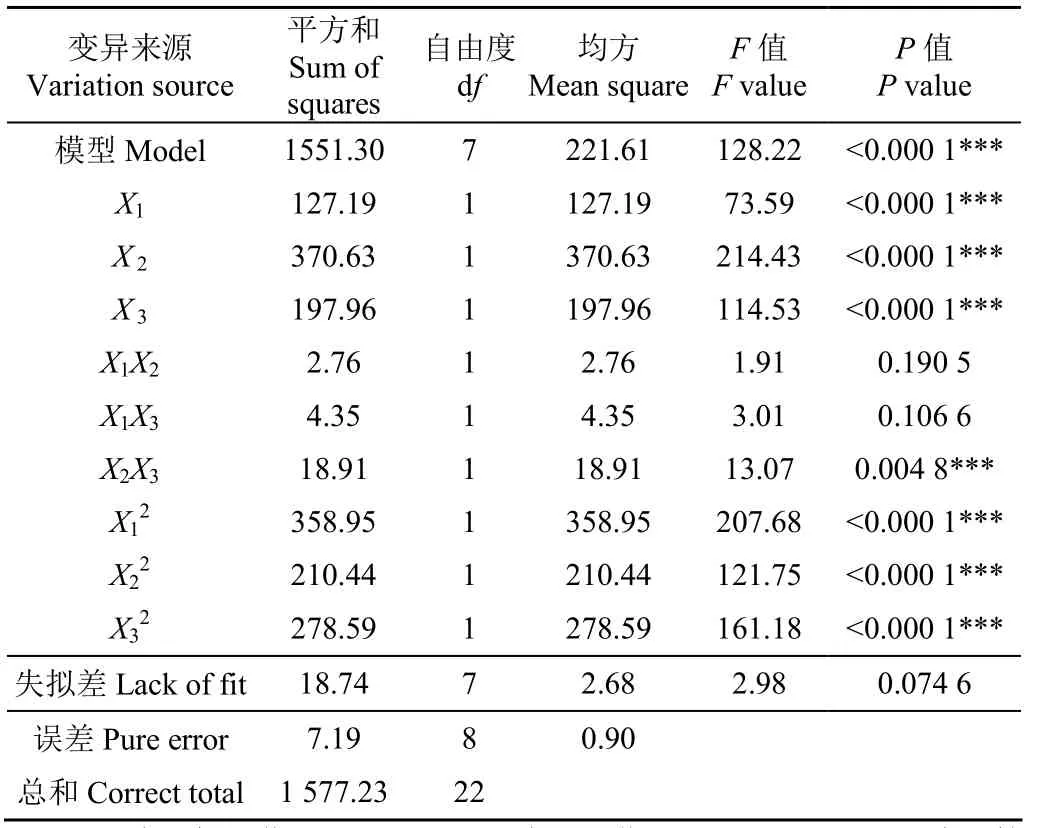
表3 开沟深度合格指数的方差分析Table 3 Variance analysis for the ditch depth qualification index

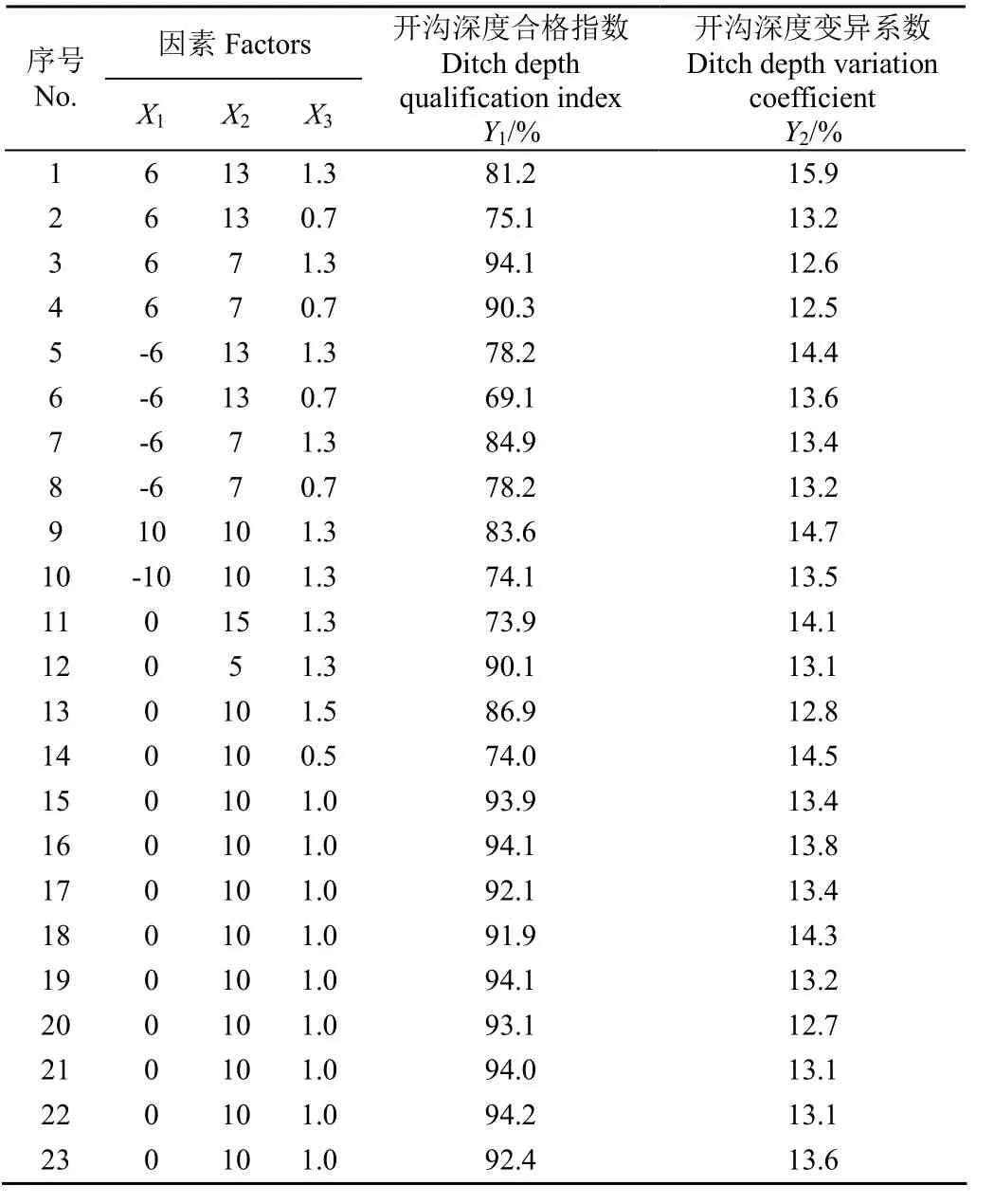
表2 试验方案及结果Table 2 Experimental design and results

对上述回归方程进行失拟性检验，证明试验指标与因素间具有显著的二次关系（P＞0.1）。

2）开沟深度变异系数Y2的显著性分析

通过对数据的分析，开沟深度变异系数Y2方差分析如表4所示。由表4可知，试验模型显著（P＜0.01），主因素中弹簧刚度对于指标影响极显著，初始牵引角对于指标影响显著，作业速度对于指标影响不显著；交互项中初始牵引角和弹簧刚度的交互作用X1X2对指标影响最大，为较显著。将不显著因素并入残差项后再次进行方差分析，结果如表 4所示，得到各个因素与指标间的回归方程如式（33）所示。

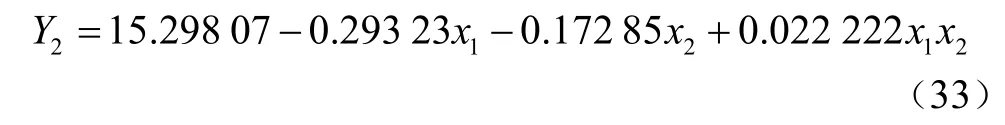
对上述回归方程进行失拟性检验，证明试验指标与因素间具有显著的二次关系（P＞0.1）。

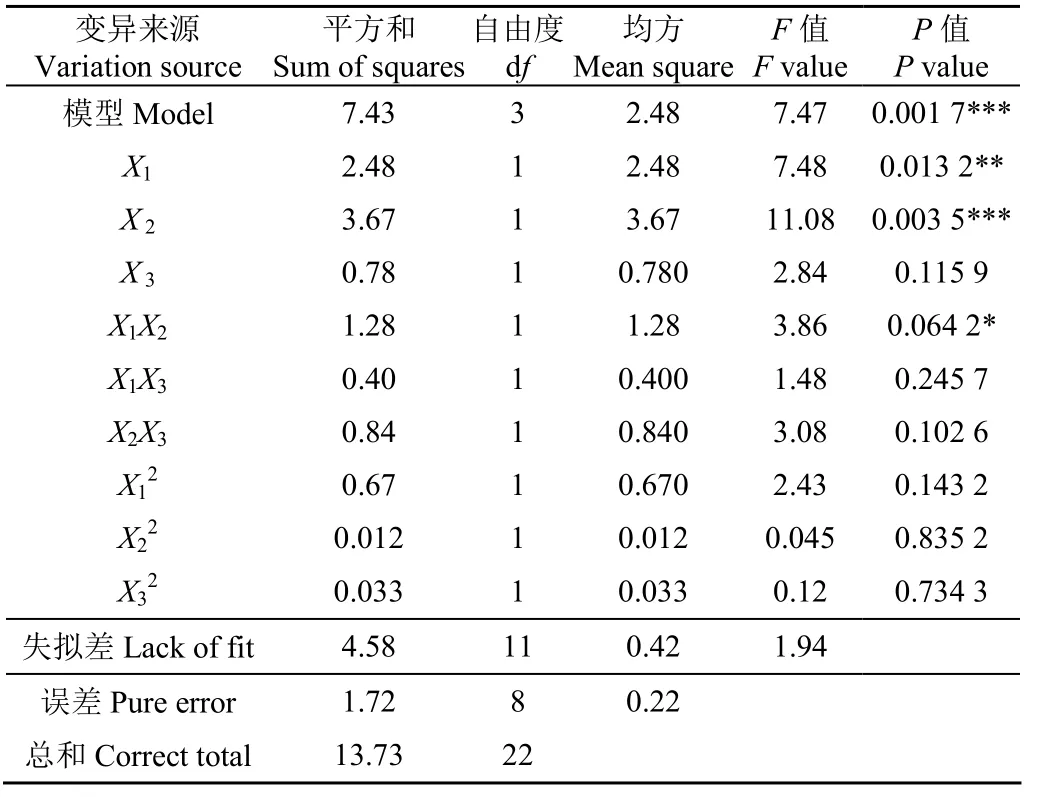
表4 开沟深度变异系数的方差分析Table 4 Variance analysis for variation coefficient of ditch depth

4.3.3 参数优化与验证响应曲面分析

通过Design Expert 8.0.6软件对数据的处理，得出初始牵引角、弹簧钢度、机具作业速度之间的交互作用对开沟深度合格指数、开沟深度变异系数 2个试验指标的响应曲面，如图7、8所示。

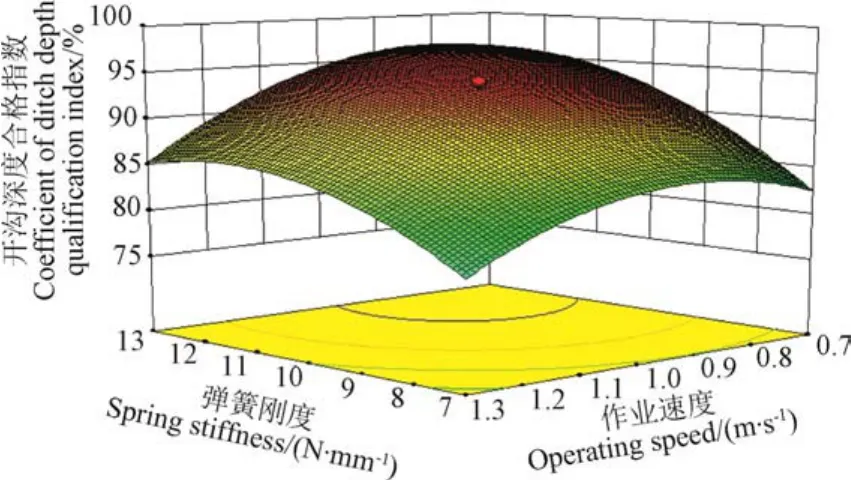
图7 开沟深度合格指数的双因素响应曲面Fig.7 Response surface of double parameters about coefficient of ditch depth qualification index

对于开沟深度合格指数，当初始牵引角为 0时，弹簧刚度与作业速度的交互作用影响如图 7所示，当作业速度一定时，开沟深度合格指数随初始弹簧刚度的增大呈现先增大后减小的趋势，其最优弹簧刚度范围是9.35～11.56 N/mm；当弹簧刚度一定时，开沟深度合格指数随作业速度增大呈现先增大后减小的趋势，其最佳作业速度 0.89～1.13 m/s。

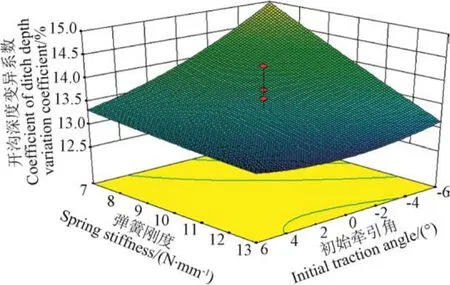
图8 开沟深度变异系数的双因素响应曲面Fig.8 Response surface of double parameters about coefficient of ditch depth variation coefficient

对于开沟深度变异系数，当机具作业速度为1 m/s时，初始牵引角与弹簧刚度的交互作用影响如图 8所示，当弹簧刚度一定时，开沟深度变异系数随初始牵引角的增大呈现减小的趋势，其最优初始牵引角范围是−1.2°～5.7°。当初始牵引角一定时，开沟深度变异系数随弹簧刚度增大呈现减小的趋势，其最佳弹簧刚度 9.62～12.80 N/mm。

4.3.4 参数优化与验证

为得到最佳的试验因素水平组合，利用Design-Expert 8.0.6软件中的优化模块对回归模型进行求解，根据马铃薯播种作业的实际工作条件、作业性能要求及上述相关模型分析结果，选择优化约束条件为

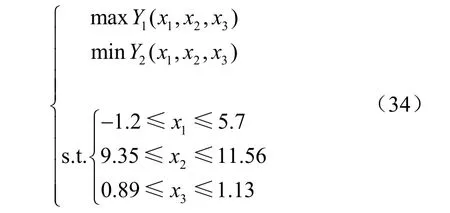
通过优化求解，得到弹簧刚度为10 N/mm，作业速度为1 m/s，初始牵引角为0时，马铃薯播种机播深调控装置的工作性能最好，此时开沟深度合格指数为96.6%、开沟深度变异系数为8.9%。

5 结 论

本文对播深调控装置进行了结构设计，主要包括平行四杆仿形机构的设计、仿形限深轮的配置和开沟器的设计，通过对播深调控装置的动力学分析，建立了开沟深度稳定性的数学模型，得出了影响马铃薯播种机开沟深度稳定性的主要因素为弹簧刚度、初始牵引角和机具作业速度。

对安装有播深调控装置的播种机进行了二次正交旋转组合试验，建立了各个因素与指标间的回归模型。通过田间试验验证了播深调控装置工作后的开沟效果。当前进速度为1 m/s，弹簧刚度为10 N/mm、初始牵引角为0时，开沟深度合格指数为96.6%、开沟深度变异系数为8.9%，满足马铃薯播种的作业要求。

本文通过对播深调控装置的动力学分析以及对开沟深度稳定性模型的建立，为马铃薯播种机播深一致性技术进步提供了参考。