基于有限元分析的矿山边坡自动数值建模与分析研究①

易红卫， 樊陵姣， 谌 涛

（湖南工学院 建筑工程与艺术设计学院，湖南 衡阳421002）

边坡具有易受影响、不确定等特性，其稳定性分析是矿山地质工程研究重点，也是一个难点问题［1-2］。边坡稳定性与地质地貌、地下矿房、人为活动等多项因素密切相关，因此在矿山地质工程建造中，设计人员需要综合各项因素，准确地评估矿山边坡情况，以满足工程设计要求［3-4］。 三维可视化数值计算模型能够体现边坡中岩石的空间分布信息，避免二维数值模拟存在的模拟层面单一的缺陷，真实展现矿山边坡地质信息，目前已成为矿山地质工程领域的研究热点，具有重要的经济意义和指导意义。 有限元分析方法是一种典型的三维数值模拟技术，可有效表达和重现矿山边坡岩土体的应力应变状态，成为边坡稳定性分析的重要依据，近年来在岩土工程，尤其是边坡问题研究中得到了广泛应用［5-6］。

本文以某开采铁矿为研究对象，采用有限元分析方法开展矿山边坡自动数值建模与分析研究，以期解决目前地质工程数值模拟中存在的问题以及数值自动建模研究中存在的不足。

1 工程概况

某开采铁矿矿区规模大，经过长年开采，该矿区形成了露天坑，分为东、西两个采区，东区用于堆积矿产开发中的废土、废石，西区用于开采。 但由于开采量大且较为频繁，该铁矿开采后形成3 个采空区，破坏了边坡内原有的平衡状态，诱发矿山边坡形变，使得矿山开采存在安全隐患。

根据采空区平面和立体图，设定边坡高度130 m。为有效避免边界效应，在边坡左右分别取70 m、前后分别取50 m，边坡总长度250 m，边坡岩体厚度110 m。边坡总共可分为5 个区域，包含凝灰岩中风化区、软弱夹层、砂质泥岩强风化区、泥砂质岩中风化区以及断层带。

2 矿山边坡有限元建模分析

2.1 计算范围设定

设定矿山边坡空间坐标，将横向宽度用X轴表示，横向高度用Y轴表示，纵向为Z轴。 计算范围设定中，取X轴方向250 m，Y轴方向110 m，Z轴方向130 m，由坡面顶部向山体内延伸。

2.2 矿山边坡岩土体材料分区

根据本文选取矿山边坡的岩土体特性，按照强风化区、中风化区、夹层和断层，将边坡的三维模型划分为5 个不同的区域，如图1 所示。

图1 矿山边坡岩土体分区图

2.3 网格划分

矿山边坡有限元法实际是通过材料分区处理，转换基本力学方程，将求解区域内的连续场函数转换为离散节点计算问题，这一计算过程是近似处理过程，因此需要对模型单元网格进行划分。 矿山边坡网格划分模型如图2 所示。

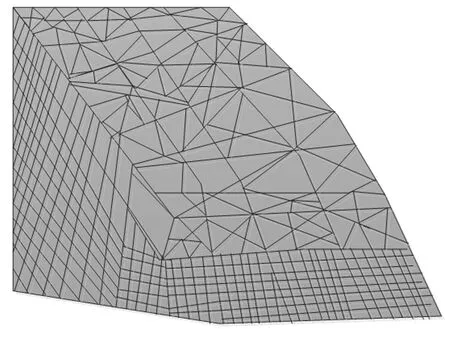
图2 矿山边坡网格划分模型

2.4 边界条件设置

将矿山边坡底面固定，边坡水平方向设置左右双向法向约束，这时坡体表面则为自由面，边界条件设置完成。 在此边界条件下，对矿山边坡的自重应力进行有限元分析，计算结果作为初始应力。

依据上述各条件设置与分析情况，完成矿山边坡有限元模型构建。

2.5 力学特性分析

针对构建完成的有限元模型，分析矿山边坡各单元的力学特性，具体使用以下3 个方程描述：

节点位移方程：

对照组与教改组期末考试成绩比较见（表2）。结果显示，教改组的期末考试成绩高于对照组，差异具有统计学意义（P＜0.05）。

节点位移与单元应力的关系方程：

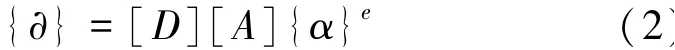
建立在单元上的结点作用力和位移之间存在的相互关联，可表示为单元平衡方程：

式中｛α｝为已划分单元中任意点的应变列阵；［A］为单元应变矩阵；｛∂｝为已划分单元中任意点的应力列阵；［D］为岩土材料弹性矩阵；［G］为单元刚度矩阵。

根据上述方程计算得出每一个单元的平衡方程，综合所有平衡方程即可完成整个有限元模型平衡性分析，实现矿山边坡自动数值建模与分析。

3 应用实例

为验证本文研究方法的有效性和可行性，选取某开采铁矿为研究实例，将其简化为如图3 所示的三维简化模型进行分析。

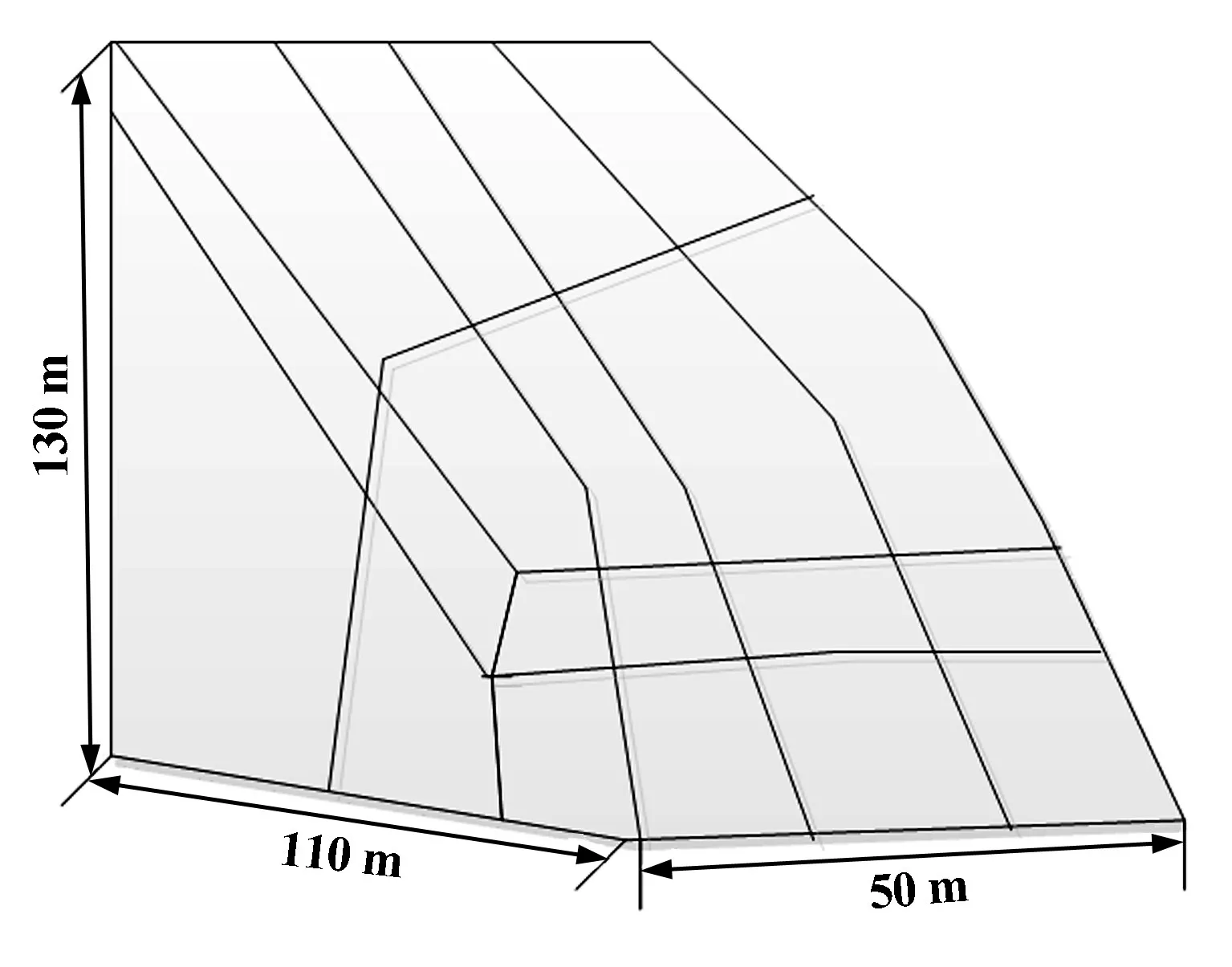
图3 三维简化模型

采用20 节点6 面体单元以及其退化形式，本构关系采用D⁃P 模型，网格划分相对较为紧密。 边坡水平面采用左右双向法向约束，很好地保证了模型的原有特性。

矿山边坡地层参数详情见表1。

表1 矿山边坡地层参数

为验证本文研究方法的可行性，选取矿房跨度、间柱宽度和顶板厚度为指标，研究本文模型条件下，矿房各结构参数对边坡主应力的影响。 设计如表2 所示的正交表。

表2 正交设计表

以表2 中3 个因素水平取值为依据，模拟3 个因素对矿山边坡表面主应力的影响，结果如表3 所示。

表3 边坡表面主应力模拟

根据表3 给出的主应力模拟情况进行了极差分析，结果如表4 所示。

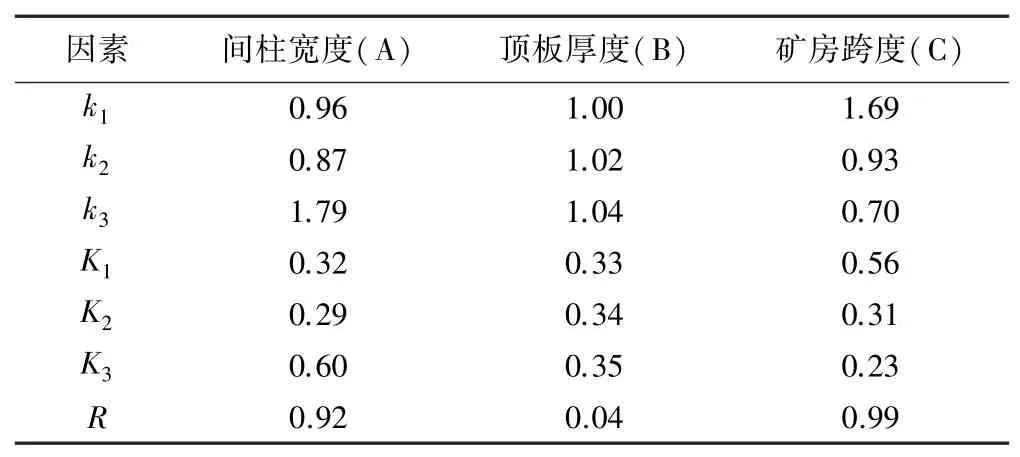
表4 极差分析结果

由表4 可以看出，矿房跨度变化时，边坡表面主应力变化最大，边坡主应力对矿房跨度的敏感性较强；间柱宽度次之；最后是顶板厚度，可见边坡主应力对顶板厚度敏感性差。 综合上述3 个因素的边坡表面主应力极差值分析，可排列得出以上3 个因素的敏感性为矿房跨度＞间柱宽度＞顶板厚度。 这一研究结论与目前公开的研究结果一致，由此验证了本文研究方法的有效性。

为进一步验证本文方法计算结果的准确性，以边坡安全系数为指标，对比本文方法和FLAC3D计算结果的准确性。 本文借鉴文献［7］中的边坡计算模型数据。 边坡安全系数的计算公式为：

式中i为边坡路径，最大取值为m；Ki为第i条路径的抗滑力；Di为第i条路径的下滑力。

利用FLAC3D方法获取的矿山边坡计算模型［7］如图4 所示。 依据强度折减法计算得出FLAC3D模型的矿山边坡安全系数为1.95。

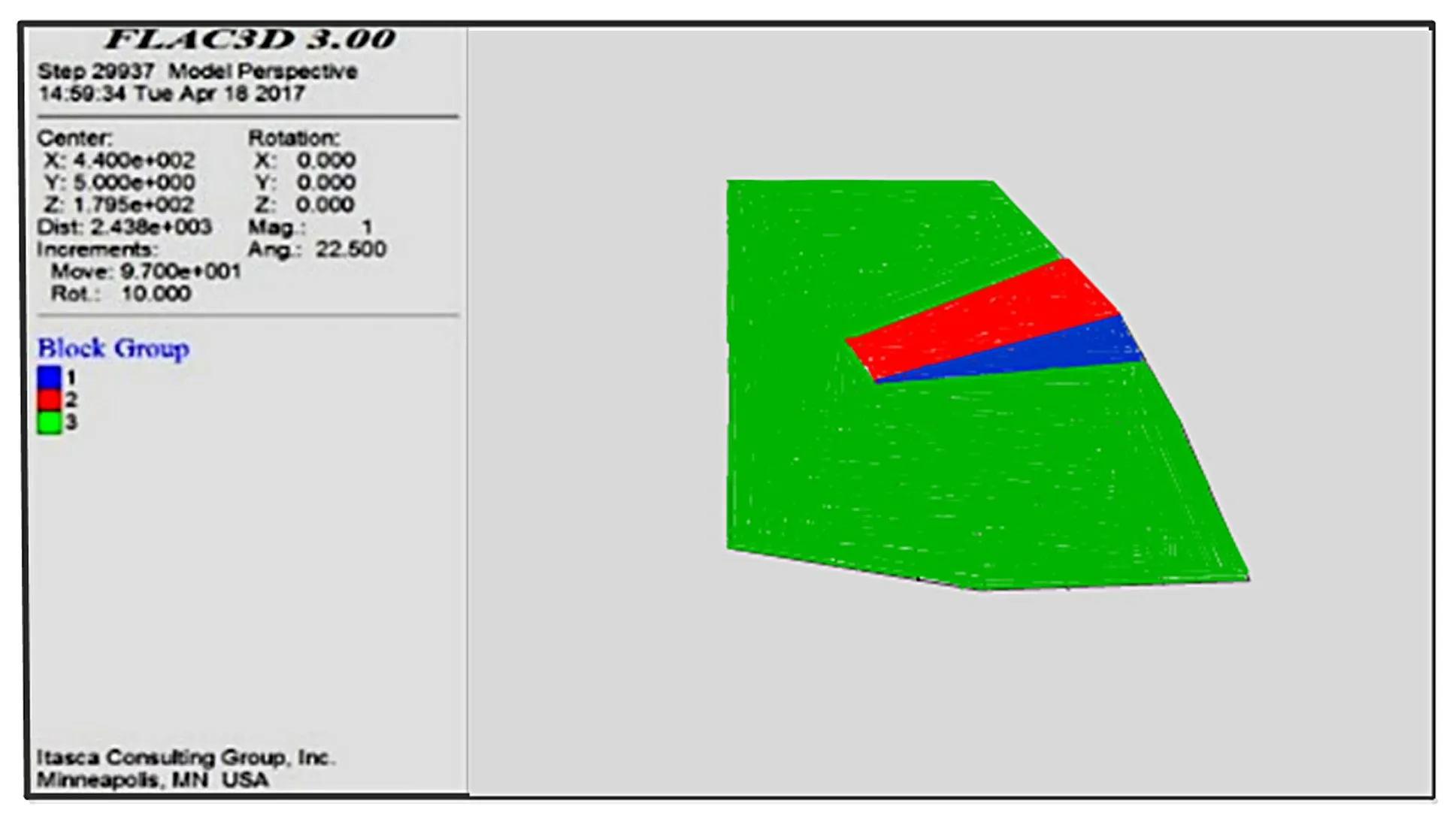
图4 FLAC3D矿山边坡计算模型

在保持与FLAC3D模型计算环境一致的情况下，依据式（4），在不同影响域尺寸下计算本文有限元分析方法获取的矿山边坡安全系数结果，如表5 所示。 由表5 可以看出，在不同影响域尺寸下，本文方法的矿山边坡安全系数数值均接近1.95，与FLAC3D模型的矿山边坡安全系数吻合度较高，由此验证了本文方法的可行性，表明本文研究方法具有一定的实际应用价值。

表5 有限元分析下矿山边坡安全系数

4 结 论

1） 基于有限元分析方法，进行了矿山边坡自动数值建模与分析研究。 有限元建模过程中网格划分步骤简洁，且对边坡的力学特性进行了分析，综合各单元的平衡方程得到了有限元模型的整体平衡方程，有效增加了矿山边坡有限元模型的准确性。

2） 使用实例验证的方式，选取模型参数敏感性和安全系数两个指标，分别验证了所研究方法的性能，结果表明，本研究方法具有一定的可行性和实际应用价值，为岩土工程研究提供了参考依据。