潮流能水平轴水轮机在剪切来流下的水动力分析①

黄 欣， 胡建新， 李 钟， 金 星

（1.浙江理工大学 机械与自动控制学院，浙江 杭州310018； 2.长沙矿冶研究院有限责任公司 海洋矿产资源开发利用研究所，湖南 长沙410012）

潮流能由于具有较强的可预测性、功率密度大、对海洋环境影响较小等特点而受到关注［1］。 以英国为例，从2003 年MCT 公司首次开发测试运行SeaFlow 机组，到2013 年TGL 公司研制1 MW 机组等，现可并网稳定运行并持续向用户输送可观的电量。 目前我国也有多家单位涉足潮流能开发领域。 哈尔滨工程大学在国内较早从事潮流能水轮机的研究，有多台水轮机组如“万向II”垂直轴直叶变桨水轮机和“海能”系列等已投入测试运行［2］。

潮流能水平轴水轮机因其结构与控制系统相对简单和功率稳定等优点，逐渐被证明是一种比较经济的潮流能转换装置［3］。

受海底地形如海底坡道、粗糙度和丘壑等的影响，潮流在海峡中的运动比较强烈，容易引起高湍度来流，并进一步形成速度沿深度变化的剪切流来流，给潮流能水轮机的运行带来挑战。 近年来，Fleming［4］和Wimshurst［5］分别模拟了由斜坡或波浪引起的剪切来流和波浪工况下的水轮机流场，研究发现剪切流动会引起载荷波动或非对称性载荷，对机组桨叶、传动链等关键零部件的疲劳载荷有直接影响。

为获得直接、精准的研究结果，本文采用基于计算流体力学（CFD）方法的全尺度数值模拟计算，建立适用于潮流能水轮机模拟的剪切来流环境，通过数值计算结果，对潮流能水轮机随时间变化的宏观力和流场特征进行系统地分析，探索水轮机在复杂工况下的水动力特性规律。

1 CFD 模型的建立

潮流能水轮机模型和数值计算取某典型潮流能水平轴水轮机模型（见图1），其中桨盘面直径D为18 m，整个三维计算域尺寸为：长度9D，深度2D，宽度4D。

图1 潮流能水平轴水轮机模型

基于OpenFOAM 计算流体力学开源代码平台，基于Navier⁃Stokes 流体动力学方程和有限体积数值离散方法，选取并行的非定常数值求解器。 基于计算效率和计算可靠性的综合考虑，将主要采用雷诺平均Navier⁃Stokes 方程（RANS）的湍流模型进行流场求解，计算域阻塞比不高于3%。

对于高湍流度剪切来流下的水轮机流场的全尺度模拟，涉及非均匀来流条件和运动边界的复杂情况。

1.1 浅水剪切流环境模型的建立

通过湍流摩擦速度得到海床处的雷诺剪切应力，假设沿垂直方向，雷诺剪切应力呈线性分布，可以得到剪切来流入口处雷诺剪切应力在垂直方向的分布。 结合湍流涡粘系数在垂直方向的分布，从而得到剪切来流入口处的速度分布，同时得到湍动能在入口处沿垂直方向的分布。 入口速度和湍动能在垂直方向的分布可以通过参考文献［6］，在入口处计算获得。

1.2 运动边界的模拟

对叶片绕水平轴的转动如图2 所示，结合OpenFOAM中的AMI（Arbitrary Mesh Interface），设置网格间的交接面，通过动网格功能明确转动速度和转动轴等。

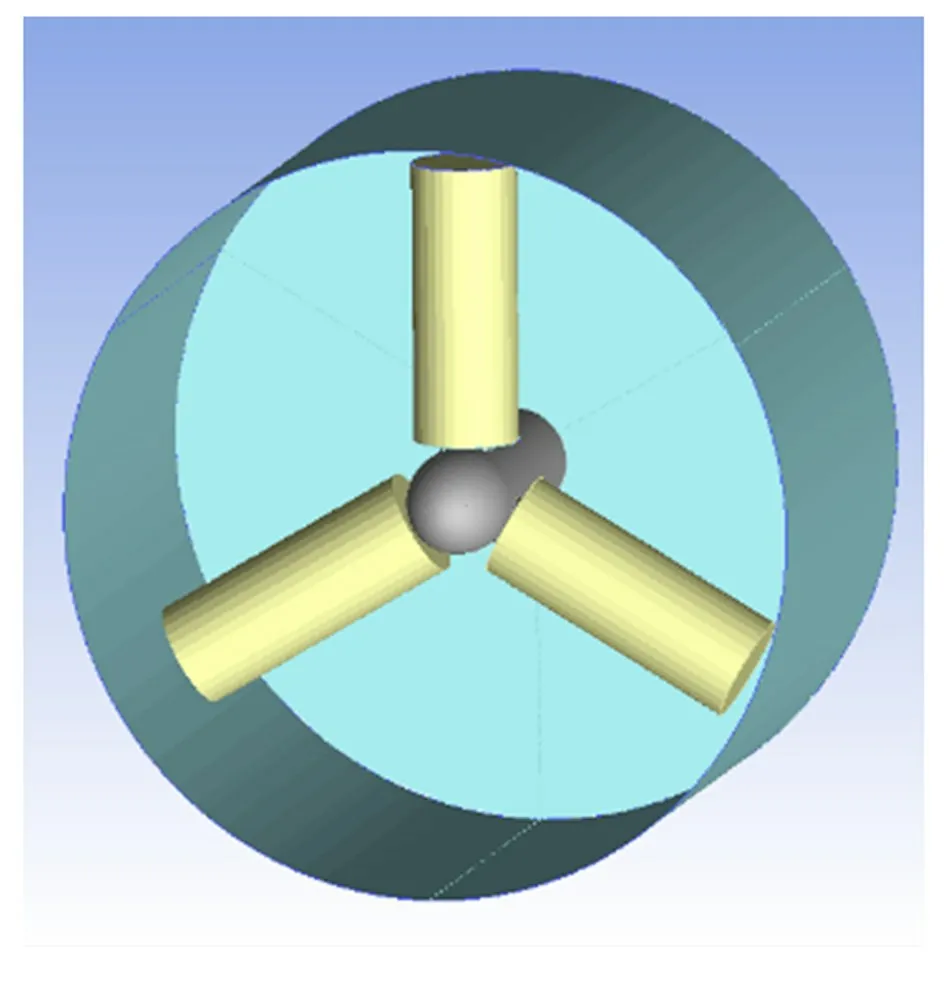
图2 转动界面示意图

同时，对每个叶片部分进行独立的结构化网格划分，保证圆环面和叶尖底面之间的网格质量，如图3 所示，用于捕捉叶尖梢涡和局部的压力、速度分布等。

图3 叶片附近的结构化网格

2 数值计算结果分析

基于以上计算模型，采用保证相同的有效水流速度（uref），选取不同的叶尖速比（tip speed ratio，TSR），可系统研究叶轮转速对流场流动特征和水轮机结构受力特征的影响和剪切来流对水轮机受力的影响。

水轮机的轴向力系数CT、轴向扭矩系数CQ和平均功率系数Cp可表示为：

式中T为轴向力；Q为轴向扭矩；为平均水轮机功率；ρ为水密度；Ar为转子扫略面积；R为转子半径。

通过分别对水轮机在均匀流和剪切流工况中进行数值模拟计算，得到水轮机的性能曲线如图4 所示。对比水轮机在均匀流工况和剪切流工况下的受力平均值，可以看到水轮机叶轮在不同工况下的水力性能曲线相似，平均轴向力系数随叶轮转速增加而增加，最高的平均功率系数对应唯一的叶轮转速。 水轮机叶轮的整体平均受力在剪切流工况中未受到明显影响。

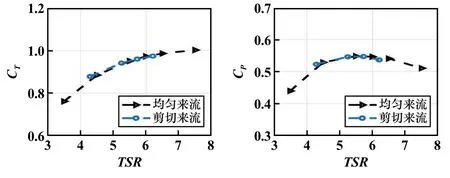
图4 不同工况下，水轮机叶轮平均轴向力系数和平均功率系数随叶尖速比的变化

水轮机在均匀流工况中的受力不随叶片的周期性转动而变化。 但在剪切流工况中，叶片在旋转过程中，经历了剪切流工况的不同高度位置的来流流速变化。因此进一步对水轮机单个叶片和整个叶轮在剪切流工况下的轴向力系数和扭矩系数进行分析和研究。 水轮机单个叶片的瞬时轴向力系数和瞬时轴向扭矩系数随旋转周期n的变化如图5 所示，整个叶轮的轴向力系数和扭矩系数随旋转周期的变化如图6 所示。

图5 剪切流场工况中，不同叶尖速比下水轮机单个叶片的瞬时轴向力系数和瞬时轴向扭矩系数

图6 剪切流工况中，不同叶尖速比下水轮机叶轮的瞬时轴向力系数和扭矩系数

由图5 可以看出，单个叶片的轴向力系数和扭矩系数在旋转周期内出现了明显的周期性变化，这是由于单个叶片在周期性旋转运动中经历了剪切来流不同位置的水流速度。 单个叶片的轴向力系数随转速增大而增大，扭矩系数随转速增大而减小。

尽管单个叶片受到周期性的轴向力和轴向扭矩，但水轮机的3 个叶片相差120°的相位角，将其受力相加，得到如图6 所示的叶轮瞬时受力系数，可见叶轮轴向力系数轴向和扭矩系数较平稳，且随着叶尖速比增大，叶轮轴向力系数变大，轴向扭矩系数逐渐减小。

将单个叶片周期内瞬时轴向力系数和扭矩系数的变化幅值与平均值相比，得到幅值变化率如表1 所示。可见幅值变化率随叶轮转速增大而增大，即叶轮转速越快，水轮机叶片在剪切流工况下的周期性变化越明显，扭矩系数的振荡幅值变化率高达35.6%，轴向力系数的振荡幅值变化率可达17.2%。

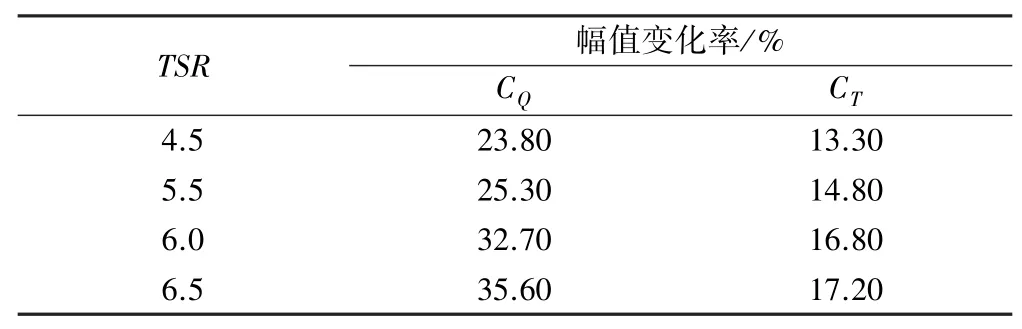
表1 剪切流中瞬时轴向力系数和扭矩系数在不同叶尖速比下的幅值变化率

3 结 论

通过数值模拟研究了潮流能水平轴水轮机在均匀来流和剪切来流工况下的水力性能，得出如下结论：

1） 水轮机整个叶轮的总体平均受力在剪切流工况中未受到明显影响。

2） 单个叶片的瞬态轴向力系数和瞬态轴向扭矩系数在旋转周期内出现了明显的周期性变化，且周期性变化幅值随转速增大而增大。

3） 非定常的瞬时轴向扭矩和力的周期性振荡容易引起单个叶片的结构性振动，可能对水轮机的机械结构造成影响。