数学猜想使学生在课堂上“活”起来

科学家牛顿有句名言：“没有大胆的猜想，就不可能有伟大的发明和发现。”因此，在小学数学教学中，运用猜想可以营造学习氛围，激起学生学习兴趣、主动参与数学知识探索和研究的过程。

纵观数学发展历史，很多著名的数学结论都是从猜想开始的，所以在数学教学中，应当鼓励学生大胆提出猜想，发表独特见解。使学生在数学课上真正地“活”起来。因此，针对《圆锥的体积》这节课的内容特点，我采用了猜想——验证的教学方法。

【教学过程】

一、创设情境，诱发猜想

（一）课件演示，呈现问题情境

本节课导入：

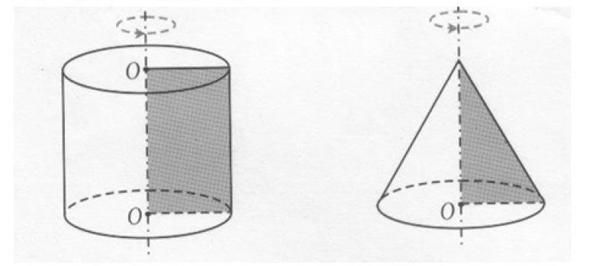
1、我们认识了圆柱和圆锥，下面我们再来回顾一下它们的形成过程，请仔细观察大屏幕。

2、你观察到了什么？

生（1）：长方形旋转一周形成圆柱，三角形旋转一周形成圆锥（你观察的真仔细）

生（2）：三角形的面积是长方形面积的1/2（一半）

（二）产生猜想

3、三角形的面积是长方形面积的1/2（一半），那它们旋转后所形成的圆锥和圆柱的体积又会有什么样的关系呢？请你猜测一下

问题一提出，学生们立刻活跃起来

生：圆锥体积是圆柱体积的一半、三分之一等

二、实践操作，验证猜想

选取实验方法

4、同学们敢于大胆猜测真令人佩服，你们能想办法来验证自己的猜想吗？小组讨论打算通过什么方法来验证。

生：（1）都倒满水再称重量从而找到关系

（2）先往圆锥里装满沙土，然后倒入圆柱

（3）先往圆柱里装满沙土，再倒进圆锥里

这时我顺势展示我所准备的学具

（一）出示准备的学具，自由选择学具

老师为你们准备了圆锥和圆柱，每个小组先思考用什么学具进行实验，派代表到前边领取学具。

学生领学具的状态：

多数的小组进行认真思考后到前边慎重的拿走学具;有的小组没有深入进行思考，到前边一会儿拿起这个，又看看那个，不知拿哪个好，但最后还是侥幸拿对了;还有的小组不加思索随便拿起学具就走。

选完学具后及时进行监控

哪个小组来汇报，你们选择了什么学具？

生：等底等高的圆锥和圆柱

（1）怎么知道等底等高？

利用手中的学具进行演示;放在平面比高、再把底重合，来说明等底等高;把圆锥放在圆柱里）

怎么进行实验的？你们的实验结果是什么？（小组到前边边操作边说）这时学生得到结论是圆锥体积是圆柱体积的1/3，仍然会忽略“等底等高” 这一前提，这时选错学具的小组自告奋勇，说出自己选取的学具，没有找到这二者的关系，从而对其他小组的汇报进行了补充，只有等底等高的圆柱和圆锥才具有这样的关系，这时也使选对学具的小组由感性认识上升到理性认识。学生间的互补突破了教学的重、难点。

看来圆锥的体积我们可以借助圆柱的体积公式来推导，圆柱的体积公式谁还记得？（V=Sh）由此学生推导出圆锥的体积计算公式是（V=1/3Sh）

通过本小节内容，培养学生推理能力。促进学生从具体的操作过渡到内部语言。

（二）汇报实验

这时学生得到结论是圆锥体积是圆柱体积的1/3，仍然会忽略“等底等高” 这一前提，这时选错学具的小组自告奋勇，说出自己选取的学具，没有找到这二者的关系，从而对其他小组的汇报进行了补充，只有等底等高的圆柱和圆锥才具有这样的关系，这时也使选对学具的小组由感性认识上升到理性认识。学生间的互补突破了教学的重、难点。

（三）归纳小结

看来圆锥的体积我们可以借助圆柱的体积公式来推导，圆柱的体积公式谁还记得？（V=Sh）由此学生推导出圆锥的体积计算公式是（V=1/3Sh）

通过本小节内容，培养学生推理能力。促进学生从具体的操作过渡到内部语言。

【教学反思】

数学猜想实际上是一种数学想象。从心理学角度看，是一项思维活动，是学生有方向的猜测与判断，包含了理性的思考和直觉的推断;从学生的学习过程来看，猜想是学生有效学习的良好准备，它包含了学生从事新的学习或实践的知识准备、积极动机和良好情感。因此，在第一环节中演示圆柱和圆锥的形成过程，为学生产生猜想指明方向，避免了学生的“瞎猜”。

数学知识的抽象性与儿童思维的形象性是一对矛盾，解决这一矛盾的有效途径之一就是操作。在学生有了初步的猜想后，我积极鼓励学生开阔思维，鼓励学生积极的寻找猜想的依据，索求猜想的合理性和准确性，不迷信已有的结论，不满足现成的答案，要通过自己的实践操作，来检验猜想的真伪。为了更好地使猜测不流于形式，为教学起到更好的作用，我还通过访谈进行了前测。题目如下：（1）你们还记得圆柱体积计算公式吗？100%学生准确回答出了公式（2）那你们有人知道圆锥体积公式吗？这时有18名学生把手举得高高的，异口同声地说：圆锥体积=1/3×底面积×高，字母表示：V=1/3Sh

还没学呢，你们就这么多人知道，真了不起！能告诉我你们怎么知道的吗？

有的说我自己预习的;有的说我哥（姐、爸等）教我的;有的说我奥数课上早学了等。圆柱体积公式你们在课上自己推導出来了，老师这有学具，

谁能试着选出学具，推出圆锥体积公式。有的学生拿学具时，不加思索地就拿了两个，有的学生在那挑来挑去，不知该拿哪个，还有的学生比了比圆柱和圆锥后拿走了。这时我立刻追问拿等底等高学具的学生，你干嘛选这样的学具呀？

得大小一样才能找到关系呀！

通过访谈，我清晰地看到，本班学生中有75%的学生通过各种途径已经知道了圆锥体积公式，只有25%的学生不知道公式。但在75%的学生中，只有5名学生，也就是只有27%的学生知道在选取学具时要选一样大小的（学生的描述），（也就是等底等高的学具）但学生只是直观上选取，而没有学生能说出要选取“等底等高”的圆柱和圆锥，这也使我肯定了自己在学具的提供上能促进学生思维的提升。使学生知道知识的探究是需要科学、严谨的态度。

在前测题中明显看到学生选“等底等高”的学具不是真的理解研究他们的关系要具备等底等高这一前提，而是直觉在操纵他们，而通过选错学具的小组，实验得不到确切的关系时，从而使学生思维得以提升。

古人说：“授人之鱼，只供一餐所需;而给人之渔，终身受用不尽。”素质教育也要求学生不仅“学会”，更要“会学”。这节课我导学生在猜想的基础上运用动手实验、合作交流、归纳推理、尝试练习等方法，使学生成为数学学习的主人，让每个学生“动”起来，让课堂的气氛活跃起来。

总之，数学猜想能激活学生的求知欲，而且猜想所经历的体验将展示他无法估量的创造潜能。数学猜想使学生在课堂上“活”起来。

作者简介：马春明（1978年6月—），女，汉族，北京，北京广播电视大学本科，北京市朝阳师范学校附属小学黄胄艺术分校，研究方向：数学。