基于Weibull分布函数的浆板热风干燥特性

2020-07-23孔令波董继先尹勇军

中国造纸 2020年6期

杨兴孔令波，* 谢姗董继先尹勇军

（1.陕西科技大学机电工程学院，陕西西安，710021；2.广西大学轻工与食品工程学院，广西南宁，530004）

浆板是纸浆经过脱水后形成的一种便于储存和运输的片状物，是造纸和其他生产的重要纤维原料之一。浆板的热风干燥是以被加热的空气作为干燥介质，通过连续不断地吹过湿浆板表面，由于水蒸气分压差的作用促使水分由毛细孔隙向外扩散并蒸发，来完成干燥的一种干燥方式。由于其干燥效率高、装置简单、干燥条件可控性，已成为浆板最主要的干燥方法。在纸张的干燥过程中，干燥特性描写的是纸张含水率随时间变化的曲线，涵盖了干燥过程中动态变化的所有信息[1]。为了更好地反映植物纤维物料在热风干燥过程中的动态信息，已有很多半经验和半理论模型被用于描述纸浆或纸制品的干燥特性，如Motta Lima等人[2]对比了自然对流和强制对流下纸张干燥特性的区别，通过Hodges 模型得到了一般的纸张干燥速率曲线；Vieira 等人[3]研究了废纸浆的干燥动力学特性，用统计学模型表示了废纸浆干燥终止与初始含水率的比值和干燥温度、风速等干燥条件之间的关系；张琳[4]分析了风速和温度对纸浆模塑干燥速率和效率的影响，发现Page 模型可以很好地描述纸浆模塑的干燥过程；刘卫涛等人[5]对纸浆模塑干燥的动力学模型进行了分析，发现Logarithmic模型可以很好地描述纸浆模塑的干燥过程。虽然这些模型较好地模拟了纸浆或纸制品的干燥特性，但模型中出现的参数都为经验常数，参数本身并没有实际的物理意义，也就不能与干燥工艺有效结合，从而降低了模型的适应性和适用价值。

由瑞典科学家Weibull[6]提出的Weibull 分布函数改进了以上模型缺点，同时由于其简单灵活，较好的兼容性和适应性，近年来被广泛应用于各种物料的干燥动力学研究[7-9]。宋镇等人[10]用Weibull 函数描述了不同干燥方式下的茯苓干燥特性；王鹤等人[11]和巨浩宇等人[12]分别用Weibull 函数描述了枸杞微波干燥和真空脉动干燥过程。李亚丽等人[13]研究了不同热泵式冷风干燥条件下双孢菇的干燥特性，利用Weibull 分布函数对双孢菇热泵式冷风干燥过程中的水分扩散机制进行了分析；黎斌等人[14]用Weibull 函数描述了真空干燥下花椒干燥动力学特性。这些研究的进行说明了Weibull模型在干燥特性研究中的可行性和适应性。

本课题研究了热风温度和风速对浆板干燥特性的影响，利用Weibull 分布函数对其动力学过程进行了模拟，建立了热风温度、风速与模型中参数的定量关系，计算了浆板干燥过程的水分扩散系数和活化能。

1 实验

1.1 实验材料

未漂硫酸盐针叶木商品浆板，产自加拿大，原始尺寸850 mm×800 mm×1 mm。为方便进行干燥实验（考虑到干燥室托盘的尺寸大小），把原始大尺寸的浆板切成尺寸为80 mm×80 mm 的小浆板，在水分渗透充分均匀的情况下，制备初始含水率约为70%的若干实验样品。

1.2 实验装置及方法

热风干燥实验装置如图1 所示。空气经进气阀进入实验设备，由风机提供动力，通过控制阀控制空气流速，经过加热器加热，送入到干燥室中（断面尺寸≥140 mm×200 mm）。送风的流速和温度分别由孔板流量计和进口温度计测量，干燥室内的温度分别由湿球温度计和干球温度计测量，浆板质量由外置的HZTA1000型号的电子天平称量。干燥后的废气一部分通过排出阀排出，另一部分通过循环阀与新鲜风混合后循环再利用。

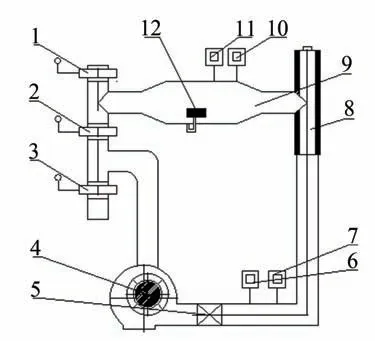
图1 热风干燥实验装置结构示意图

实验开始前，设置热风温度和风速为实验所需值，待系统稳定运行5 min 后，将浆板平行放入到载物台上开始干燥实验。实验前10 min每30 s迅速取出浆板放入电子天平上（HZT-A1000）记录一次浆板质量，之后每60 s记录一次，直至浆板质量基本保持不变，结束实验。然后，依次设置不同的热风温度（80、90、100℃）和风速（1.87、2.00、2.48 m/s），重复上述实验步骤，得到不同干燥条件下的浆板干燥特性数据。

1.3 数据分析

（1）水分比MR

不同时刻浆板水分比MR表达式见式（1）。

式中，Xt为t 时刻浆板的干基含水率，g 水/g 纤维；X0为浆板的初始干基含水率，g 水/g 纤维；Xe为浆板的平衡含水率，g水/g纤维。

浆板在t时刻的干基含水率Xt（g水/g纤维）的计算见式（2）。

式中，mt为浆板干燥t时刻的质量，g；mg为浆板绝干时的质量，g。

（2）干燥速率DR

浆板的干燥速率DR（g 水/（g 纤维·min））的计算见式（3）。

式中，Xt1、Xt2分别为t1、t2时刻浆板的干基含水率，g水/g纤维。

（3）Weibull分布函数

参照文献[15-16]，基于Weibull 分布函数的水分比MR可以表示为式（4）形式。

式中，α 为尺度参数，min，表示干燥过程中的速率常数，约等于干燥过程中浆板脱去63%水分所需要的时间；β 为形状参数，其值与干燥过程中干燥曲线的形态有关；t为浆板干燥时间，min。

（4）有效水分扩散系数Deff

Fick 扩散方程可以用来描述浆板降速干燥特性。对于薄片状物料，在干燥时间足够长的情况下，Fick扩散方程的解可以简化为式（5）[15]。

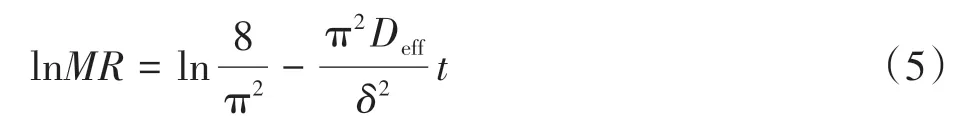
式中，Deff为有效水分扩散系数，m2/s；δ 为浆板的厚度，m；t为干燥时间，min。

有效水分扩散系数Deff被广泛用于描述下降速率期间的干燥过程，但是不适用于描述干燥前期存在延滞阶段的物料[16]。Weibull 模型在不考虑水分运动特性的情况下对评估有效水分扩散率具有重要意义。估算水分扩散系数Dcal的表达式见式（6）。

式中，r 为浆板的体积等效半径，即视浆板薄层为体积球体时的半径，本次实验r=0.012 m。

有效水分扩散系数Deff与估算水分扩散系数Dcal关系[16]见式（7）。

式中，Rg是一个与几何尺寸有关的常数。

（5）活化能Ea

计算出有效水分扩散系数Deff后，根据Arrhenius方程，可以得到有效水分扩散系数与温度的简化关系，见式（8）。

式中，D0是扩散常数，m2/s；Ea为干燥活化能，kJ/mol；T 为浆板的热力学温度，K；R 为理想气体常数，取8.314 J/（mol·K）。

将式（7）代入到式（8）可得式（9）。

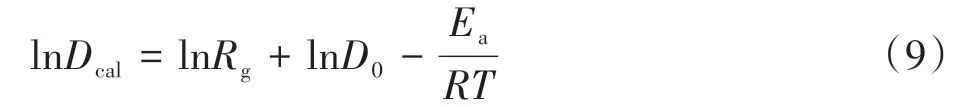
lnDcal与1/T 呈线性关系，由直线的斜率就可以计算出浆板干燥活化能Ea。

1.4 数据处理

采用SPSS 21 软件对模型进行非线性回归分析、Origin 11软件对分析结果进行绘图分析。模型的优劣程度由决定系数R2、卡方χ2、均方根误差RMSE 评价，决定系数R2越大，卡方χ2和均方根误差RMSE越小，说明模型预测值与实验值越契合。计算公式见式（10）～式（12）。

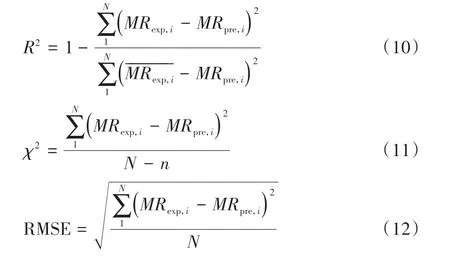
式中，MRexp,i为利用模型预测的水分比；MRpre,i为干燥实验实测的水分比；N 为实验测量次数；n 为公式中参数个数。

2 结果与讨论

2.1 热风温度对浆板干燥特性的影响

图2 为热风风速2.48 m/s 时不同热风温度下的浆板水分比曲线。从图2 中可以看出，当热风温度从80℃上升到100℃时，干燥时间由26 min 下降到20 min，这是因为随着热风温度的增高，浆板间传热温差梯度提高，浆板内部传热驱动力增大，从而有利于内部水分的迁移和外表面水分的蒸发。

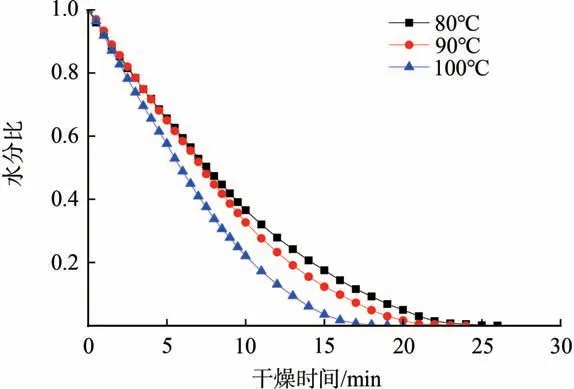
图2 不同热风温度下的浆板水分比曲线

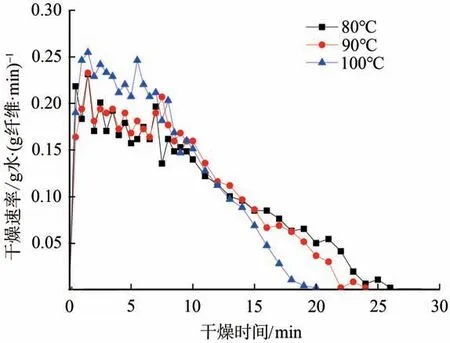
图3 不同热风温度下的浆板干燥速率曲线

图3 是热风风速为2.48 m/s 时不同热风温度下的浆板干燥速率曲线。由图3可知，浆板干燥过程呈现出3个阶段：升速阶段、恒速阶段、降速阶段。随温度的上升，恒速阶段时间缩短；降速阶段降速幅度增大，且曲线斜率随干燥时间增大而减小。热风温度升高可显著提高浆板的平均干燥速率，从而缩短其干燥时间。当热风温度从80℃上升到100℃时，恒速阶段干燥速率提升了约24%，相对应的最大干燥速率从0.22 g水/（g纤维·min）增加到0.25 g水/（g纤维·min）。

2.2 热风风速对浆板干燥特性的影响

图4 为热风温度80℃时不同热风风速下的浆板水分比曲线。从图4 中可以看到，随着热风风速由1.87 m/s 提升到2.48 m/s，干燥时间由30 min 降至26 min。这是由于热风风速的提高，增加了浆板表面的对流传热系数，从而提高了对流传质的效果。热风风速2.00～2.48 m/s之间较热风风速1.87～2.00 m/s之间干燥曲线差异变小，这是由于随着浆板外部水分气化速率大于内部水分迁移速率，浆板的表面气化已经不是主要的影响因素，改善表面气化条件达不到预期。

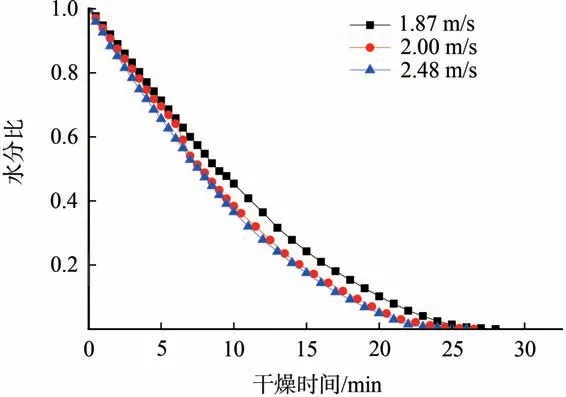
图4 不同热风风速下的浆板水分比曲线

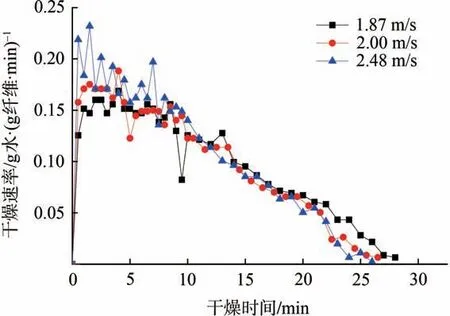
图5 不同热风风速下的浆板干燥速率曲线

图5 为热风温度80℃时不同热风风速下的浆板干燥速率曲线。由图5 可知，干燥过程同样呈现升速、恒速、降速3个阶段；随热风风速的增大，恒速阶段时间缩短；降速阶段降速幅度增大，且曲线斜率随干燥时间增大而减小。干燥速率随热风风速的增加而增加，尤其在恒速阶段，这与表面对流传热系数的增加有很大关系。当热风风速从1.87 m/s 上升到2.48 m/s时，恒速阶段干燥速率提升了约14%，相对应的最大干燥速率从0.16 g 水/（g 纤维·min）增加到0.23 g 水/（g纤维·min）。

2.3 基于Weibull分布函数的干燥特性模拟

使用SPSS 软件，基于不同干燥条件下的浆板干燥数据，对Weibull 分布函数的参数（尺度参数α、形状参数β）进行回归模拟，结果如表1所示。由表1可见，决定系数R2值在0.9960～0.9975 之间、卡方χ2值在2.78×10-4～4.29×10-4之间、均方根误差RMSE值在0.016～0.021 之间，表明Weibull 函数拟合出的曲线与实验得到的曲线有较高契合度，可以用来描述浆板的干燥动力学过程。

2.3.1 尺度参数α的影响因素

尺度参数α是干燥过程中的速率常数，约等于干燥过程中浆板脱去63%水分所需要的时间，即α 越大，表明干燥时间越长。由表1 分析可知，α 值随热风温度和风速升高而减小，当热风风速为2.48 m/s、热风温度由80℃升高到100℃时，α 值从9.667 min 降至7.383 min；当热风温度为80℃、风速由1.87 m/s增加到2.48 m/s 时，α 值从11.342 min 降至9.667 min。由此可见，尺度参数α 值大小受热风温度、热风风速大小影响。

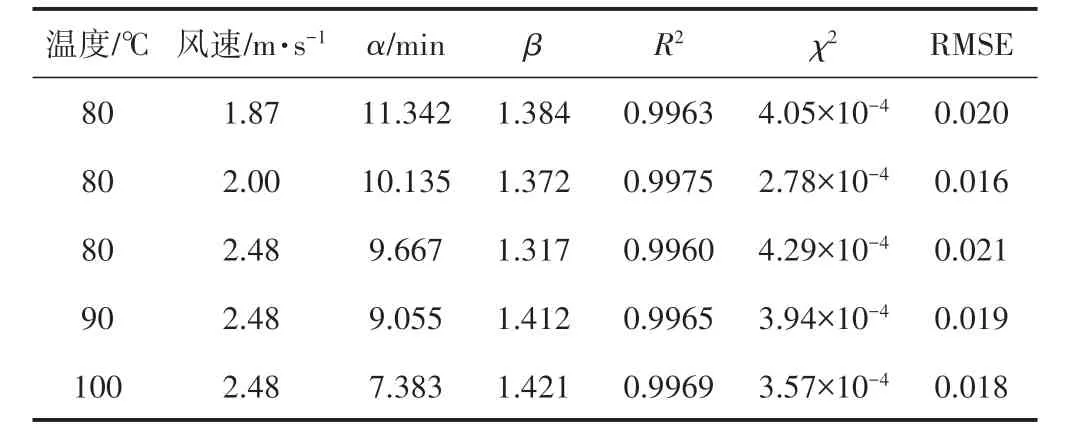
表1 不同干燥条件下Weibull函数模拟结果

2.3.2 形状参数β的影响因素

研究表明，β 值决定着干燥曲线的形状。β越小，开始时的干燥速率越快，当形状参数β在0.3～1之间时，表示物料在干燥过程是由内部水分扩散控制，即表现降速干燥的特点；形状参数β 大于1 时，干燥曲线呈现出Z字形态，表示物料在干燥前期存在延滞阶段[16]。由表1可知，β在1.317～1.421之间，表示浆板干燥过程存在延滞阶段，干燥过程并不完全由内部水分扩散控制。由表1 分析可知，β 值随热风风速的升高而减小，当风速由1.87 m/s 增加到2.48 m/s 时，β值从1.384 降至1.317，这与Corzo 等人[17]研究结果基本一致。

2.3.3 Weibull模型的求解

以热风温度T、风速V 为自变量，尺度参数α、形状参数β 为因变量。按照式（13）、式（14）进行拟合推导其定量关系。

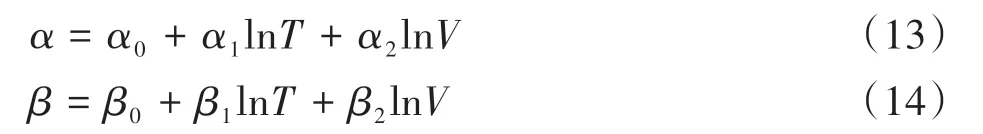
式中，α0、α1、α2和β0、β1、β2均为待定模型系数。

利用SPSS 软件，拟合各待定模型系数值，代入到式（13）、式（14）中表示为式（15）、式（16）。

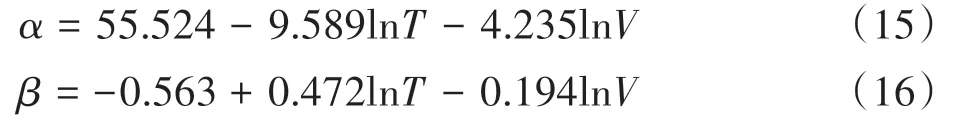
将式（15）、式（16）代入到式（4）中，则浆板热风干燥的Weibull分布函数模型方程可表示为式（17）。

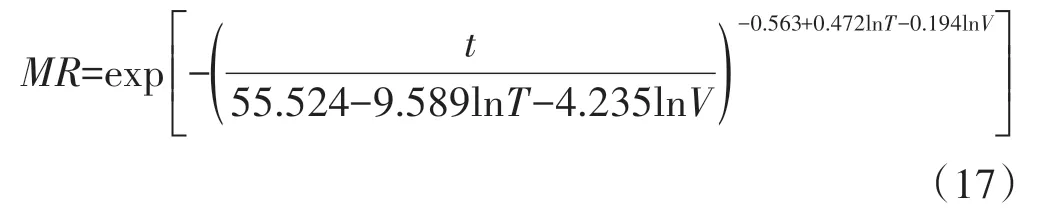
2.3.4 Weibull模型的验证

图6 给出了浆板干燥在不同热风温度下Weibull模型水分比MR 的预测值与实验值的关系，其数据基本处于斜率45°的直线附近，这表明可以用Weibull模型来描述浆板的干燥动力学过程。

2.4 有效水分扩散系数

将实验得到的MR 与t 的关系转换为lnMR 与t 的关系，并进行线性拟合，根据式（5）拟合方程的斜率为-π2Deff/δ2，计算有效水分扩散系数Deff；代入式（6）中计算估算水分扩散系数Dcal。不同条件下浆板热风干燥Deff和Dcal如表2 所示。在热风温度80～100℃（风速2.48 m/s）下Deff为2.567×10-10～3.631×10-10m2/s，在热风风速1.87～2.48 m/s（温度80℃）下Deff为2.077×10-10～2.567×10-10m2/s。

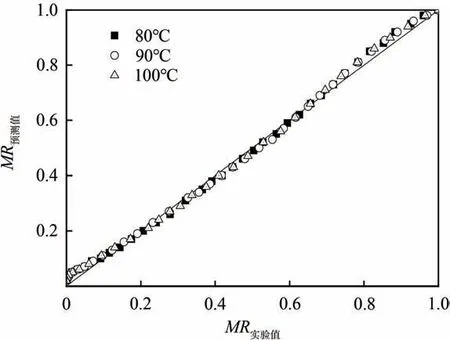
图6 Weibull模型预测值与实验值之间的关系

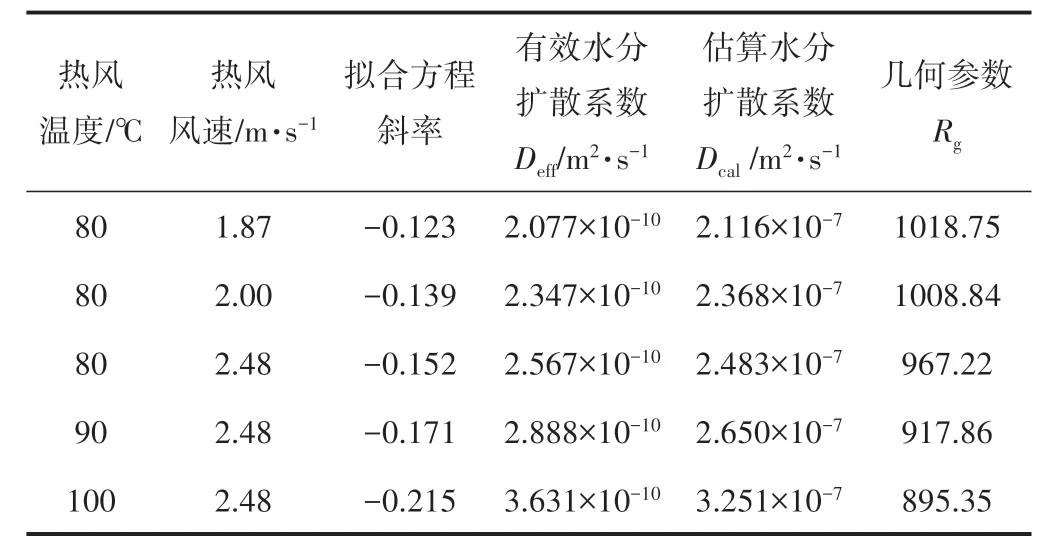
表2 不同干燥条件浆板有效水分扩散系数和几何参数结果

Dcal在2.116×10-7～3.251×10-7m2/s之间，且随α值的增大而减小。几何参数Rg也是一个非常重要的物理参数，有研究发现Rg值是一个与无关的常数[18]。由表2 可看出，几何参数Rg值的变化范围为895.35～1018.75。出现这种差异的原因可能是随着热风温度和热风风速的增大，浆板内部纤维形态及其分布发生了不同程度的变化。

2.5 干燥活化能

干燥活化能表示浆板在热风干燥过程中蒸发单位质量的水分所需要的能量，通过干燥活化能可以看出浆板干燥的难易程度，可以据此估算出干燥能耗。一般地，干燥活化能越大说明需要的能量越多。干燥活化能的大小主要与物料的种类、组成、组织状态和几何形状等有关。针对浆板热风干燥，在风速2.48 m/s时，根据式（8）将lnDcal与1/T进行拟合，根据拟合直线的斜率，计算出浆板干燥的平均活化能为14.8 kJ/mol。该值略低于纸浆塑模包装制品的干燥活化能（15.754 kJ/mol）[4]，说明在浆板热风干燥过程中水分较容易蒸发。