借用真题“同构” 破解一道压轴题

杜海洋

(四川省成都经济技术开发区实验中学校 610000)

一、引题呈现

成都七中2019-2020学年上期高2022届半期考试压轴题22题：

设函数fk=2x+(k-1)2-x(x∈R，k∈Z).

(2)若2m+f1(m)=5，f1(2n)+2log2(n-1)=5，求m+n的值.

解析(1)略.

二、真题再现

(2009·辽宁)若x1满足2x+2x=5，x2满足2x+2log2(x-1)=5，x1+x2=( ).

分析本题涉及的是两个非整式方程，其中一个是指数超越方程，一个是对数超越方程，这两种方程均不在高考考纲范围之内，因此此题中不用分别解出两个方程，分别求出x1，x2，再求x1+x2．尤其高一学生才学完指对函数，又属于第一期半期考试题，所以解决本题的突破口应该是从指对本身隐含的关系去入手破解.我们知道人教A版必修一指对数这部分内容重点突出指对互化，单调性，尤其图象的运用更明显，随后提及同底的指对函数定名互为反函数.并在教材76页探究与发现研究互为反函数的两个函数图象之间的关系.接下来笔者就利用学生最近发展区知识进行探究.

探究一、转化化归为同种函数

由于两方程不能求解，但又要求出两根的和，唯一的想法只有想到含两根的式子均是某一方程的两根(容易联想到一元二次方程的两根之和)，这样才能够建立两者关系，所以只有将两方程在形式上进行化归统一.

方法一巧妙配凑，转化为指数函数，并利用指数函数的单调性求解.

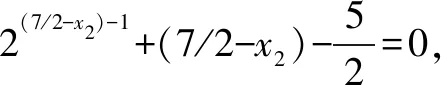
缠尸布碎成了絮，纷纷扬扬地飘落，吹散了一地。尸体重新落回台面，脸面朝下，后背朝上，已一丝不挂。天葬刀并不稍停，锋利的刀刃在筋骨与关节间如龙游走。猩红的血顺着刀身上纤细的云纹倒流而上，所经之处，刀身闪现起荧荧红光。血水继续蜿蜒向上，直流入刀柄前端墨玉骷髅的口中。

探究二、代数换元，结合配凑合理转化

分析尤其一些代数式求值问题，可将代数式整体用新元表示，这样一来多建立了方程，与题中的方程联合构成方程组，进而相互可进行代换转化.

方法三令x1+x2=t，则x1=t-x2，代入2x1+2x1=5得2t-x2=5-2(t-x2)=2x2-2t+5.

方法四令x1+x2=t，则x2=t-x1，代入2x2+2log2(x2-1)=5进行变形.下同解法三.请读者自推.

方法五配系数换元

分析先由题中已知分别将x1、x2所满足的关系表达为2x1=2log2(5-2x1)…系数配为2是为了与下式中的2x2对应2x2+2log2(x2-1)=5.观察两个式子的特点，发现要将真数部分消掉求出x1+x2，只须将5-2x1化为2(t-1)的形式，则2x1=7-2t，t=x2.

由题意2x1+2x1=5①,2x2+2log2(x2-1)=5②.

所以2x1=5-2x1，x1=log2(5-2x1)即2x1=2log2(5-2x1).令2x1=7-2t，代入上式得7-2t=2log2(2t-2)=2+2log2(t-1).

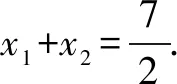
同理，本法也可将对数结构向指数转化.(请读者自己证明)

探究三、数形结合(利用一对反函数图象)

分析试题中求x1+x2，即会联想到中点坐标公式，又由题意指对涉及到同底，联想到指数函数y=2x与对数函数y=log2x的图象关于y=x对称这一特性，利用该特性可以应用数形结合思想解决．

从以上几种解法可以看出，这是一道指对互化的经典试题.为了追求在结构上统一，利用转化思想实行了互化.其中运用构造方程和函数思想，尤其是探究一体现了函数的单调性的运用.方法六将同底的指对函数图象关系运用达到极致，数形结合显直观.

那么以上两题能在教材找到相应的题根吗？回答是肯定的.此上两题其实就是来自教材习题变式.

三、试题探源

(苏教版必修一课本习题)已知x+lgx=10,y+10y=10，求x+y的值.

(请大家借助教材习题及高考试题可以进行不同的变式，期待更多精彩类题呈现)

其实我们知道很多新问题是在原问题的基础上进行了某种程度的改头换面，或者进行了适当的变式或包装，只要能看透变式与包装背后的本质的东西，那么问题无论如何变幻莫测，解决起来我们总能游刃有余和得心应手.我们深知随着高中数学学习，以后涉及知识点多，范围广，每次题目不断变化更新的同时考查方式也是多种多样，但数学考查知识点是相对固定的.因此在平时学习或复习备考时注重回归教材，以教材为根据地，认真研究例题、习题，进行一题多变，一题多解.在强化数学思维、方法的训练的同时归类和比较方法的优劣，以及找到共性，提高自己的学习能力，刷高质量题，进一步在学习备考中取得事半功倍的效果.