揭秘高考中的充要条件命题特点

陈国林 韩景岗

(1.江西省南昌市东华理工大学理学院 330013；2.山东省邹平县黄山中学 256200)

从近几年的高考试题中可以观察出关于充要条件的考查一般常为选择题或填空题，难度不大.但是考查情况多样，常与向量、三角函数、不等式、方程、集合、数列、平面几何和复数进行考查.考查形式主要有两种：一是判断指定的条件与结论之间的关系；二是探索求某结论成立的充要条件、充分不必要条件或必要不充分条件.下面就一起去赏析近几年的高考试题.

一、充要条件与向量结合的考题策略

例题1(2016年北京卷)设a，b是向量，则“|a|=|b|”是“|a+b|=|a-b|”的( ).

A.充分而不必要条件 B.必要而不充分条件

C.充分必要条件 D.既不充分也不必要条件

解析若“|a|=|b|”，则以a，b为邻边的平行四边形是菱形；若“|a+b|=|a-b|”，则以a，b为邻边的平行四边形是矩形.故“|a|=|b|”是“|a+b|=|a-b|”的既不充分也不必要条件.故选D.

二、充要条件与三角函数结合的考题策略

例题2 (2015年陕西卷)“sinα=cosα”是“cos2α=0”的( ).

A.充分不必要条件 B.必要不充分条件

C.充分必要条件 D.既不充分也不必要条件

解析若sinα=cosα，则cos2α=cos2α-sin2α=0，充分性成立；反之，若cos2α=cos2α-sin2α=0，则sinα=±cosα，必要性不成立．因此，“sinα=cosα”是“cos2α=0”的充分不必要条件.故选A.

三、充要条件与不等式结合的考题策略

例题3 (2015年天津卷)设x∈R，则“|x-2|<1”是“x2+x-2>0”的( ).

A.充分而不必要条件 B.必要而不充分条件

C.充要条件 D.既不充分也不必要条件

解析因为|x-2|<1⟺-10⟺x<-2或x>1，所以“|x-2|<1”是“x2+x-2>0”的充分不必要条件．故选A.

四、充要条件与集合结合的考题策略

例题4 (2014年湖北卷)设U为全集，A，B是集合，则“存在集合C使得A⊆C，B⊆UC”是“A∩B=∅”的( ).

A．充分而不必要条件 B．必要而不充分条件

C．充要条件 D．既不充分也不必要条件

解析若存在集合C，使得A⊆C，B⊆UC，则A∩B⊆C∩(UC)=∅；反过来，若A∩B=∅，由韦恩(Venn)图可知，一定存在集合C使得A⊆C，B⊆UC.故选C.

五、充要条件与数列结合的考题策略

例题5 (2016年天津卷)设{an}是首项为正数的等比数列，公比为q，则“q<0”是“对任意的正整数n，a2n-1+a2n<0”的( ).

A．充要条件 B．充分而不必要条件

C．必要而不充分条件 D．既不充分也不必要条件

六、充要条件与平面几何结合的考题策略

A．充分而不必要条件 B．必要而不充分条件

C．充分必要条件 D．既不充分也不必要条件

七、充要条件与复数结合的考题策略

例题7(2014年浙江卷)已知i是虚数单位，a，b∈R，得“a=b=1”是“(a+bi)2=2i”的( ).

A．充分不必要条件 B．必要不充分条件

C．充分必要条件 D．既不充分也不必要条件

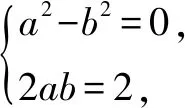
关于“充要条件”的高考命题特点进行分析，题目难度不大，主要考查基本知识基本技能，常常以小题的形式结合其它知识点进行综合考查.要想熟练掌握此类问题，一方面需要胆大细心，以免掉进题目中所设置的陷进.另一方面，在平时学习中需要注意基础知识的掌握，因为此类试题的命题范围较为灵活.