巧交汇 妙破解——一道江苏模拟解析题的多解

周建平

(江苏省苏州市相城区陆慕高级中学 215131)

平面几何与解析几何分别是初中与高中两个阶段的知识点，在高中的解析几何问题中，经常渗透平面几何的知识，巧妙把两者加以有机融合，共同构建起优美的数学题目，考查初高中的数学知识与能力.因此，在破解一些相关问题中，有效利用平面几何知识在解决解析几何问题中的作用，多一点思考，就能少一点运算，优化解题过程，达到事半功倍的效果.

一、问题呈现

问题(2019届江苏省靖江高级中学高三12月月考)已知圆O：x2+y2=1，定点A(3，0)，过A点的直线l与圆O相交于B，C两点，B，C两点均在x轴上方，如图1，若OC平分∠AOB，则直线l的斜率为____.

本题以解析几何中的圆为问题背景，通过直线与圆的位置关系的建立，结合角的平分线的条件的介入，最终落到直线的斜率的求解上.巧妙把解析几何、平面几何加以交汇，把圆的方程、直线的方程、直线的斜率、角平分线等相关知识加以链接，进而达到知识交汇，能力拓展的目的.

二、多解思维

思维角度1：(三角参数法)

解法1 设C(cosθ，sinθ)(θ为锐角)，则知B(cos2θ，sin2θ)，而A(3，0)，结合kAB=kAC，

由于θ为锐角，可得

思维角度2：(三角形面积转化法)

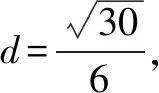
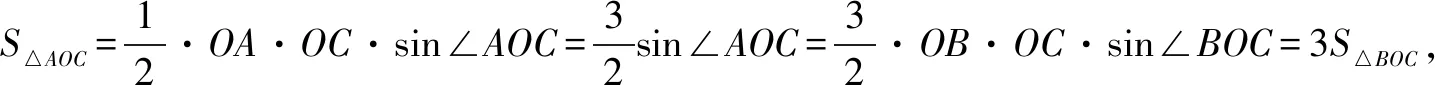
思维角度3：(角平分线定理法)

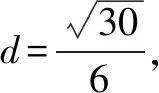
思维角度4：(坐标法)

结合角平分线定理的转化得到AC=3BC，设出点B(x1，y1)，点C(x2，y2)，利用向量的坐标关系式得到两者之间的关系式，并借助代换法来求解关于点B(x1，y1)两个方程，得以确定其坐标，再利用直线的斜率公式求解即可.

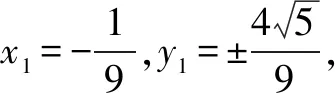
解析几何是通过平面直角坐标系，建立点与实数对之间的一一对应关系，运用代数方法来研究对应的几何问题.而平面几何更注重直观，更注重于“形”，解析几何依赖运算，更侧重于“数”.在实际解决此类综合问题的过程中，若能将“形”与“数”有机结合，善于从图形的几何关系中抓住几何本质，挖掘几何内涵，并加以合理运用，可以有效拓宽解题思路，减少解析几何的运算量，缩短思维步骤，优化解题过程.