辩证思维下高中数学例题讲解分析

苏灿强

(福建省安溪第一中学 362400)

数学学科学习过程中主要核心素养之一就是逻辑推理能力，也是数学教学的关键所在，夯实学生数学学习基础.数学逻辑关系的培养，解题时明确条件与结论之间的因果关系，逐步形成数学逻辑思维能力.这就需要教师有目的地培养学生辩证思维习惯，提升数学课堂教学质量.

一、深入挖掘数学教材，找寻存在的辩证关系

数学主要研究现实世界数量关系、因果逻辑和空间形态等的一种推理性学科，它虽来自于生产生活实践，却又在生产生活中有着广泛应用，同时也在科学研究领域担任重要角色.利用数学这一特性，采用辩证唯物主义的思想和观点对其内容进行阐述，以此解释数学中隐藏的辩证思想，培养和引导学生辩证思维能力的发展.

如，“数”的概念的产生和发展就是辩证思维的最好案例.“负数”搞定了“不能减”的问题；“分数”搞定了“不能整除”的问题；“无理数”搞定了“开方不尽”的问题；“虚数”搞定了“负数不能开偶次方”的问题.当“数”的定义从有理数扩展到“实数”后，增加了数的连续性，完成了四则运算以及开方中存在的问题，但却因为域的增加失去了数的可数性；当“数”从“实数”扩展到“复数”后，不仅能够对代数进行开方，同时解决了“负数”不能开偶次方的问题，但却不总是能对数的大小进行比较.如此引导学生不断地发现问题，分析问题，进而解决问题，然后又发现新的问题，新的矛盾，如此反复，对学生辩证思维进行培养，如此帮助学生正视问题，面对现实，积极主动先找解决问题的方法，帮助学生形成正确的人生观，以便学生未来更好地进入社会.

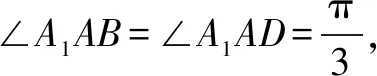
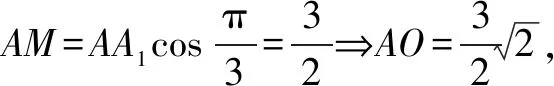
二、打破常规解题模式，培养逆向思维能力

数学题目解答的第一步就是审题，学生审题时要梳理其中包含的知识点.实际解题时遇到难度较大的题目时，大部分学生会出现畏难情绪，这时教师要启发学生转变思维，利用逆向思维思考问题，从相反角度思考问题，可能会收到意外效果.高中数学学习中逆向思维集中体现的就是反证法与补集方法.

解析如果按照常规解题方法解答这道问题，需要将不等式转为两个不等式组，接着对这个不等式组进行求解.但如果学生引入补集思想，只需要求出一个不等式组的解即可.

这道例题解决时，需要利用全集I求出解集，就是运用典型的辩证思维.分析这道例题时可以发现，数学知识点学习时不能形成思维定式，眼光也不能只关注一个点，通过现象看到题目本质，拓展学生思维，并习惯从不同教学视角思考与分析问题，也只有这样才能提升解题效率与准确率.

三、选择合适的切入点，提高数学解题效率

数学习题解决时需要选择合适的切入点，也就是选择解题角度.如果数学题目条件比较繁杂，学生审题后经常性出现思维混乱情况，无法选择正确解题方向，也就无法提升解题效率.出现这种情况的根本原因就是学生无法从辩证角度看待数学问题，数学问题条件之间、条件与结论之间本身就是对立与统一的，造成解题时出现半途而废的情况.

例2已知函数f(x)=2sinx-xcosx-x，f(x)的导数为f′(x).(1)求证：区间(0,π)内f′(x)存在唯一零点；(2)当x∈(0,π]时，函数f(x)≥ax，求a的取值范围.

解这里主要讲解第2个问题.通过题设：

f(x)≥ax及f(π)=0⟹a≤0 ①.

由第一问得出区间(0,π)内f′(x)存在唯一零点，假设为x0②.

当x∈(0,x0)时，f′(x)>0；当x∈(0,π)，f′(x)<0.

∴(0,x0)区间内f(x)单调递增，区间(x0,π)内f(x)单调递减.

又∵f(0)=0，f(π)=0,

∴当x∈(0,π)时，f(x)≥0,当a≤0,x∈(0,π),ax≤0,得：f(x)≥ax③.

∴a取值范围为(-∞,0] ④

评析这道题目不同于常规题型，组合学生熟悉的三角函数与一次函数，成为考查学生三角函数与一次函数，很多学生看到题目后无从下手.第二个问题中主要考查不等式恒成立求参数取值范围的问题，并结合常用的解题方法，利用“充分必要法”讨论分界点或缩小讨论范围.

四、掌握构造函数技巧，合理利用辩证思维

在高考数学试题的解题中，我们需要通过构造条件与结论之间的“桥梁”来实现解题，其中构造桥梁的方法就是“构造法”.构造函数法就是通过对题目的透彻分析，然后构造出对应的函数，并借助函数的相关性质来完成求解.

总之，数学解题中培养学生辩证思维，也就是发展角度正确认识数学知识.辩证思维建立在客观认知的基础上，创新数学解题方法与角度.数学解题时运用辩证思维，要打破传统解题思维的限制，大幅度提升数学课堂教学质量与效率，全面落实核心素养的要求.