运用同构式 巧解数学问题

姜 磊

(江苏省南京市板桥中学 210039)

一、不等式问题中的同构式

例1证明：当x>0时，恒有(ex-1)ln(x+1)>x2.

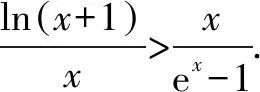
二、函数问题中的同构式

对于高中生而言函数问题一直是难点之一，那么除了常规的函数方法外，运用同构式解决函数问题也不失为一个不错的选择.

例2设f(x)=x(e2x-a)，若f(x)≥1+x+lnx恒成立，则实数a的取值范围是多少？

三、解析几何问题中的同构式

例3已知如图1，A、B为抛物线C:y2=4x上的两个点，且直线AB过定点(1,0)，现存在C外一点P，使得AP、BP的中点均在C上.(1)求点P的轨迹方程；(2)求S△PAB的取值范围.

反思上述例题看上去似乎并没有运用同构式的相关知识，但是实际上这是一道“类阿基米德三角形”问题，整体的运算过程是“同构”于阿基米德三角形性质的证明过程的，因此该题从本质上依然是一道同构式问题.

同构式是数学和谐美、对称美的集中体现，其公式看起来简单，但是想要合理运用却很难，如果学生可以将同构式的相关知识在高中数学的解题中加以合理运用可以发现它不仅可以简化运算，更可以理清思路，拓展思维.