例谈导数定义法求不定式极限的策略

纪定春 姜艳红 蒋红珠

(1.四川师范大学数学科学学院 610068；2.四川省资中县第一中学 641200;3.广东省广州市广东华南师范大学数学科学学院 510631)

一、导数定义与不定式极限简介

导数定义设函数y=f(x)在x=x0处的瞬时变化率为

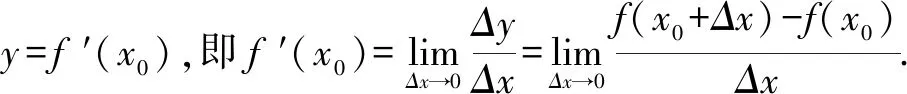
这就是函数定义在点x=x0处的导数.

不定式极限若函数f和g满足

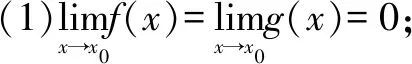
二、导数定义法求不定式极限的策略

1.直接利用导数定义法

例1(2017年全国高考数学文科卷Ⅱ第21题)设函数f(x)=(1-x2)ex.

(1)讨论f(x)的单调性；

(2)当x≥0时，f(x)≤ax+1，求a的取值范围.

解析问题(1)解答，略.对于问题(2)，显然可以使用分离参数法，需要进行分情况讨论.

当x=0时，显然有(1-02)e0≤a·0+1，故不等式恒成立，所以a∈R.

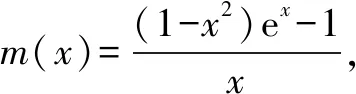
可以利用导数研究函数m(x)的单调性，容易说明函数m(x)在区间(0,+)上是单调递减函数，故

显然这是一个不定式极限，注意到分式的分母结构，考虑直接构造导数的定义.

令函数n(x)=(1-x2)ex-1，则有n(0)=0.

可得a的取值范围为[1,+).

评注该试题为典型的求不定式极限问题，分母的结构和导数定义中的结构是完全相同的，考虑直接构造导数的定义.巧令函数n(x)=(1-x2)ex-1，使得分子和分母的结构与导数定义的结构相对应起来，将不定式极限转化为求导运算、分式极限化为整式极限.

2.“裂项”构造导数定义法

例2(2016年四川高考理科卷第21题)设函数f(x)=ax2-a-lnx，其中a∈R.

(1)讨论f(x)的单调性；

解析问题(1)解答，略.

由于x∈(1,+)，分离参数可得令要使得不等式在x∈(1,+)上成立，则需要a>g(x)max.

利用导数，可以研究函数g(x)的单调性和最值(极值)点，可得函数g(x)在区间(1,+)内单调递减，故

令函数h(x)=x-1-e1-x+lnx，可得h(1)=0.

由导数的定义可知，

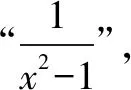
3.换元构造导数定义法

例3(2017年全国高考数学卷Ⅲ第21题)已知函数f(x)=x-1-alnx.

(1)若f(x)≥0，求a的值；(2)略.

解析对问题(1)，要使f(x)≥0，等价于x-1-alnx≥0.

考虑分离参数a，显然需要分类讨论.

在知识经济背景下，人力资源已经成为企业发展的核心。目前，我国通信行业还处于初级的发展水平，因而在诸多方面还不是十分的完善。其中，人力资源管理中，薪酬分配制度缺乏合理性就是重要的体现。现阶段，我国大部分通信公司在薪酬分配过程中，采用的分配体系都是依托岗位技能为主的等级薪酬制。显然，这种传统的薪酬分配制度难以满足员工的需求。因此，通信行业人力资源管理中薪酬分配制度必须要不断完善。

当x=1时，有f(x)≥0，所以a∈R.

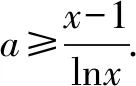
当x∈(1,+)时，分离参数，可得所以

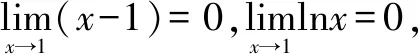
考虑构造函数g(y)=ey，则g(0)=1.

综上，a的值为1.

4.“配凑”导数定义法

例4(2018年全国卷Ⅲ理科第21题)已知函数f(x)=(2+x+ax2)ln(1+x)-2x.

(1)若a=0，证明：当-10时，f(x)>0；

(2)若x=0是f(x)的极大值点，求a.

解析问题(1)略.问题(2)是考查高考考生对极值点的定义、几何性质和代数特性(导函数在x=0处的特征)的认识，此问题设计蕴含丰富的高等数学知识内涵和背景.

由于x=0是f(x)的极大值点，由极值点的几何意义可知，存在ε>0，恒有不等式f(x)≤f(0)=0成立.

令f1(x)=2x-(2+x)ln(1+x)，g1(x)=x2ln(1+x)，则

评注该试题具有高等数学的知识背景，是一道典型的以高等数学知识来命制的函数压轴题.该试题通过反复的构造导数的定义，对极限的分子和分母逐次求导数，最终解出参数的取值范围.

三、反思与优化

通过例题4的解答过程，不难发现，“配凑”法构造导数的定义，可以看成是利用高等数学中不定式极限的求解方法——洛必达(L′hospital)法则，即

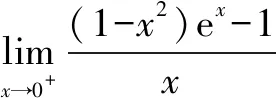
可见，通过洛必达法则来求解不定式极限，可以避免选取函数、“配凑”结构、构造导数定义的繁琐过程，极大简化运算，提高问题解决效率和准确性.洛必达(L′hospital)法则作为高等数学中求解不定式极限的重要方法，高考数学试题中常出现求解该类型的极限的问题.教学过程中可以适当地补充不定式极限的求解方法，但是不能一味地追求快速解题的“高端”方法，而是要立足于高中数学教材，在学生已有的知识基础和经验上拓展知识点，既要讲出洛必达法则的价值、优缺点、应用条件等，又要讲洛必达法则与导数之间的区别和联系，让学生真正地理解数学知识，理解知识点之间的内在逻辑联系.