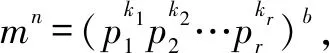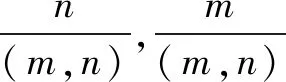由一道数学竞赛试题想到的

邓 波

(贵州省织金县第六中学 552100)

无意中，看到了手机百度推送的一道1948年莫斯科数学奥林匹克竞赛题：在自然数范围内解方程xy=yx(x≠y).我们一般会想到通过比较xy与yx的大小来完成这道题的解答.注意：在以前，自然数是不包括0的.

很明显，x、y均不等于1，否则x=y.也就是x、y均为大于或等于2的正整数.我们可以用数学归纳法证明：

当a≥5时，2a>a2；

当b>a≥3时，ab>ba.

对于前者，当a=5时，25=32>25=52.

设a=k时不等式成立，即2k>k2,

则当a=k+1时，2k+1=2k×2>k2×2=k2+k2>k2+2k+1(只要k≥3)=(k+1)2.

因此，前一个不等式成立.

对于后者，我们先证：当a≥3时，aa+1>(a+1)a.

再证后一个不等式.后一个不等式可变为：

aa+k>(a+k)a,k≥1为正整数.

当k=1时，上面已证，此时不等式成立.

设k=r时成立，即aa+r>(a+r)a,

则当k=r+1时，aa+r+1=aa+r·a>(a+r)a·a=

由数学归纳原理知，后一个不等式成立.

对于后一个不等式，我们利用导数证明更容易.这里就不作讨论.

由上面后一个不等式得知，方程xy=yx满足x

在百度视频中给出的解答如下：

(1)x,y均大于或等于2；

(2)存在自然数a,使xy=yx=ab，b为最大的自然数.(这里很明显a>1)

得出x=am,y=an(m,n都是正整数).

不妨设y>x,那么n>m,代入原方程得

amy=anx，my=nx,

y=kx.

xk-1=k(x≥2，k≥2)(注意，这时n=mk，y=an=amk=(am)k=xk，所以kx=xk).

这个方程只有一个解：x=2，k=2.

从而y=kx=2×2=4.

x=2,y=4是这个方程的解,由方程的对称性知y=2,x=4也是这个方程的解.

于是，这个方程只有两个解(x，y)=(2,4)和(4,2).

但是，只要我们稍加留意，就会问怎么从xy=yx=ab，b为最大的自然数，得出x=am,y=an.下面就来探讨这个问题.

其实，要证实解题中用到的结论，也就是要证明下面的:

命题1m,n都是大于或等于1的自然数，如果把mn写成指数最大(也就是底数最小)的幂为ab，那么m=al，l为非0自然数.

并不那么简单.

证明当m=1时，必有a=1，这时命题成立.下设m>1,自然有a>1.

下面我们证明m=al.

能不能在证明中避开整数的分解唯一性定理呢？经过我们思考，发现这是可以做到的.

我们先证

命题2 对正整数a,b,m,n,(m,n)=1，如果满足am=bn，那么存在自然数c,使得am=bn=cmn.

证明当a=1时，自然有b=1,这时c=1命题成立.

下设a>1,自然有b>1.因为(m,n)=1，由辗转相除法(即Euclid算法)(可参见[1]、[2]、[3])可知：存在整数s,t，使ms+nt=1，于是，a=a1=ams+nt=ams·ant=(bn)s·ant=(bsat)n.因为a,n为正整数，s,t是整数，bsat是正整数或者正分数，由上式用反证法可证bsat一定是正整数.

设bsat=c,则有am=(cn)m=cnm，于是am=bn=cmn.

下面由命题2证明解题中用到的、由前面的命题1可推导出来的下面命题:

对正整数a,b,m,n，如果am=bn,那么存在正整数c使得a=cl，b=cd，这里l,d均为正整数.

注意，这里的c没有解题中或命题Ⅰ中的限制.