利用“模式识别”解“隐形圆”类题

孟令艳

(江苏省连云港市灌云县杨集高级中学 222204)

一、“模式识别”基础概述

“模式识别”在高中数学中的存在，被理解为首要思维措施，解题期间学生要了解题目的具体类型，也就是把将要处理的问题结合已经处理的问题方式进行整理，把新颖的问题适当地转变，划归成熟悉的数学问题.站在思维的视角上，“模式识别”的本质便是思维定势的相反方向迁移过程，集中体现转化思想与化归思想.其中化归主要是把难以解决的问题化为可以解决的问题或者容易处理的问题，引进既有的解决问题方式，最后计算原有问题的理念.在化归开始之前，识别教学模式能力比较重要，这是数学思维化归处理的主要影响因素.

另外，模式概念可以如下理解：首先是抽象化的模式，其次是具体化的模式，在应用题列方程过程中，设置具体的问题形式，问题自身给予方程组提供具体化结构形式，模式识别后要进行巧妙的转换，因此把数学转换思维能力视作化归处理问题的第二个重点因素.需要注意的是，还有一种和数学转换可以相互触及的能力，也就是数学变式能力，尤其是代数式与超越式的转变.总之影响化归理念顺利实施的三个因素为数学转化、模式识别与数学变式.

二、利用“模式识别”解“隐形圆”类题

1.结合圆的定义，完成“模式识别”解“隐形圆”类题

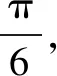
2.结合直径与圆周角关系，完成“模式识别”解“隐形圆”类题

例2若实数a，b，c成等差数列，点M(1,0)对于动直线ax+by+c=0的射影记作N，点P(2,0),计算线段NP取值范围.

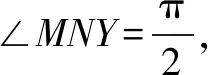
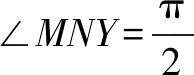
例3设圆M:x2+y2=1，圆N:(x-3)2+(y-4)2=4，Q是平面内一动点，过点Q分别作两个圆切线，切点记作A、B，如果存在QA=QB，那么点Q和坐标原点之间的距离最小数值是多少？

3.结合动点轨迹，完成“模式识别”解“隐形圆”类题

点评因为AB数值固定，所以三角形ABC的面积受到C位置的影响，也就是构建直角坐标系能够整理出点C的轨迹方程，完成面积最大值的计算.

4.结合三角代换，完成“模式识别”解“隐形圆”类题

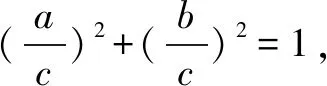
综上所述，利用“模式识别”解“隐形圆”类题研究课题的开展具有重要的意义和价值.高中学生在“隐形圆”类题的解决上一直都存在较大难度，所以教师势必要引导学生对“隐形圆”类题解决方式进行突破，充分引进“模式识别”思想，组织学生巧妙地把陌生问题转变为数值的问题，通过现有的知识经验健全问题解决体系，形成问题处理的思路，争取在较短时间内对“隐形圆”类题进行解决，提高高中学生解决问题的准确性与实效性.