等差乘等比型数列求和的另类解法——构造数列法

赵圣涛 武金仙

(山东省淄博中学 255000)

已知数列{an}满足an=bncn，其中{bn}是等差数列，{cn}是公比不为1的等比数列.数列{an}通常称为等差乘等比型数列. 该类数列求和的常规方法是错位相减法，除此之外，文献[1]中笔者从构造常数列的角度另辟蹊径，为该类问题的求解提供了一个新思路，本文分别从构造常数列和等比数列的角度，又探索出了两种求和方法，现将其介绍如下：

一、方法介绍

不失一般性，设等差乘等比型数列{an}的通项公式为an=(kn+b)qn，(其中k,b,q均为常数，且q≠1)，其前n项和记为Sn.

方法1：构造常数列{Sn+(xn+y)qn}.

对数列{an}，由an=(kn+b)qn(q≠1)得an+1=[k(n+1)+b]qn+1，由an与Sn的关系，可得关于数列{Sn}的递推关系式:Sn+1=Sn+(kn+k+b)qn+1①，下面我们考虑将该式转化成某一常数列的递推关系式的形式.设Sn+1+[x(n+1)+y]qn+1=Sn+(xn+y)qn，其中x,y是待定常数. 整理得：

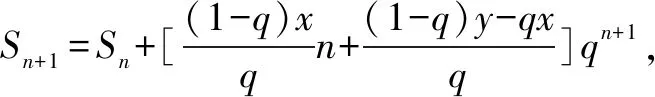
常数x,y确定后，即得常数列{Sn+(xn+y)qn}，所以Sn+(xn+y)qn=a1+(x+y)q，即Sn=-(xn+y)qn+a1+(x+y)q.

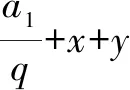
纵观上述方法，其共同点是均应用了构造数列的思想，计算量小，运算技巧的能力要求低，学生易于掌握. 方法1和文献[1]中的方法虽然都是构造常数列，但二者角度有所不同，方法1和其相比，思路更加简洁，形式简单，同时方法1和2在求解过程中均用到了待定系数法.

二、方法应用

例1已知数列{an}满足an=(2n-1)3n，求该数列的前n项和Sn.

方法1：构造常数列{Sn-(xn+y)3n}.

由an=(2n-1)3n得Sn+1=Sn+(2n+1)3n+1③.

设Sn+1+[x(n+1)+y]·3n+1=Sn+(xn+y)·3n，其中x,y是待定常数.

解得x=3,y=-3.所以数列{Sn-(n-1)3n+1}为常数列，由Sn-(n-1)3n+1=a1=3得Sn=(n-1)3n+1+3.