基于机器视觉的轴类零件定位与测量系统
2020-07-22粟序明方成刚洪荣晶赵子乐
粟序明,方成刚,洪荣晶,赵子乐
(1.南京工业大学机械与动力工程学院,江苏 南京 210009;2.江苏省工业装备数字制造及控制技术重点实验室,江苏 南京 210009)
1 引言
在工业应用中,轴类作为不可或缺的零件,广泛地应用于各类工程领域;目前,轴类零件参数测量一般通过游标卡尺、螺旋测微器以及三坐标测量等方式实现,这类测量方式都需要接触零件表面,会导致零件表面出现一定程度地损伤,而基于机器视觉的测量具有非接触性、非破坏性、精度高以及速度快等特点,因此越来越受到测量应用领域的青睐。另一方面,人员测量不可避免地出现如效率低、可靠性差、因疲劳导致误检等现象,难以满足如今制造业实行的实时、快速、在线和非接触检测的要求[1],而基于机器视觉的测量方法填补了人工检测存在的缺陷。
在机器视觉的轴类零件测量研究领域,文献[2]研究了基于MATLAB 软件结合改进的自适应中值滤波,实现了轴尺寸的测量,但是存在精度不高、未列出详细的标定与算法实现过程等问题;文献[3]研究了基于可移动的多台相机进行分段采集图像系统,结合使用远心镜头与相应的算法实现了对轴参数的提取,但是存在如不能一次进行采集、受到视场小的限制、在移动的后需要进行重新标定才能获得准确数据等等问题;
针对轴类零件的二维尺寸、倾斜角度以及中心定位检测以及以上存在的问题,开发了一套新的测量算法;实际测量的轴,如图1 所示。通过算法对CCD 相机采集来的背光轴的灰度图片进行一系列的预处理、二值化、边缘提取修正以及根据坐标跳变来确定前轴端与下个轴端之间的像素点,从而实现了对轴的关键参数一次性提取;最后,通过对CCD 相机标定与畸变校正,得到了像素坐标与实际坐标的精确转换,求得了轴的中心、关键尺寸以及在空间中的倾斜角度,同时完成了可视化GUI 设计。

图1 实际测量轴Fig.1 Actual Measurement Axis
2 CCD 相机的标定
2.1 硬件选型与平台搭建
由于相机存在畸变,会对测量精度造成很大的影响,为了获取高精度的测量值,CCD 相机的标定必不可少。采用文献[4]的黑白棋盘格标定方法,结合MATLAB 2016a 的Camera Calibration toolbox 工具箱对CCD 相机进行标定,获得其内、外参数,并转换为投影矩阵,同时依据内外参数进行了相应的畸变校正[5-6];其中,标定使用的硬件有500 万像素的CCD 相机;选用有效面积为36mm,方格尺寸为4mm 的标定板;可调节光度的背光灯源及可调相机支架;为了保证精度,选择视场为60*60mm 的平面进行标定,视觉平台,如图2 所示。

图2 视觉平台Fig.2 Vision Platform
2.2 获取相机的内、外参数
内参数反映的是相机本身的情况,外参数反映相机在空间中的具体情况,两者对后续的畸变校正具有重要作用[7-8];获取内外参数的第一步,通过CCD 相机采集15 张不同位姿的标定板图片,预先保存到一个文件夹中。然后打开MATLAB calibration toolbox载入保存好的图片,如图3(a)所示;开始运行标定,设置checkerboard square 参数为4mm,运行后可生成相应的内、外参数;标定结果的平均投影误差,如图3(b)所示。以及相机与标定模板的三维空间模型,如图3(c)所示。


图3 标定模版与结果图Fig.3 Calibration Template and Result Chart
获取的内部参数,如表1 所示。且选取一张投影误差最小的标定模版来获取外部参数,如表2 所示。
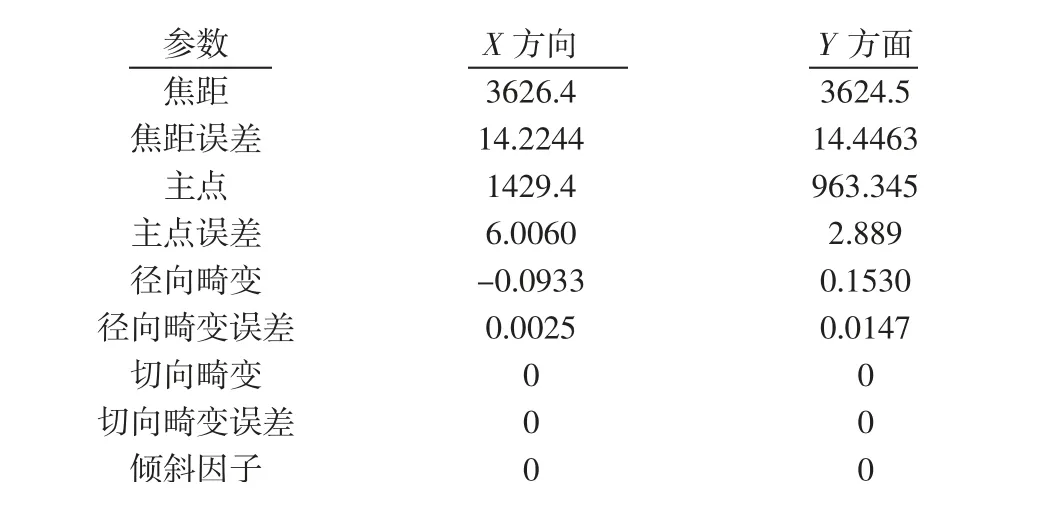
表1 内部参数Tab.1 Intrinsic Parameters
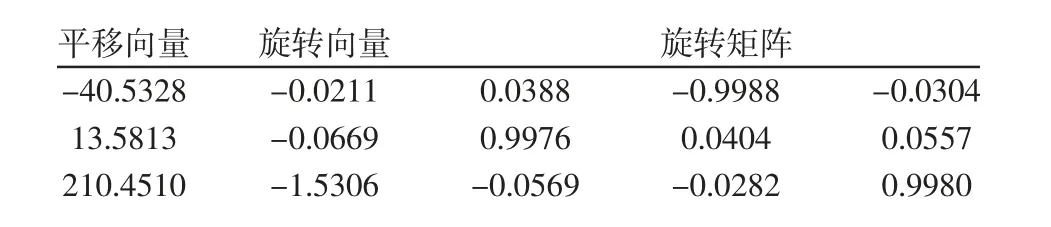
表2 外部参数Tab.2 Extrinsic Parameters
2.3 相机畸变校正
经过标定后,由获取的内部参数可知,CCD 相机存在径向畸变而切向畸变可以忽略不计,因此需要对径向进行矫正;依据Brown 模型[9]可得:

其中,(u′,v′)和(u,v)分别为矫正后和畸变下的归一化图像坐标,且,此处考虑径向和切向畸变,式(1)与式(2)中第一个括号内的值称为径向畸变量,由光学镜头径向曲率变化引起,离相机中心越远,图像点沿径向移动的变形量就越大;式(1)与式(2)第二个括号内的值称为切向畸变量,来源于相机组装过程,是指相机镜头的主光轴偏离图像中心,从而使显示的畸变图像关于中心点不对称,k1~k3为标定所得的镜头切向畸变参数,p1~p2为径向畸变。
3 定位与测量的算法
3.1 算法整体框架
针对轴的倾斜角度、关键尺寸测量及中心定位等问题,开发了一套新的自检测算法,算法具体流程图,如图4 所示。(1)采用CCD 相机获取轴的背光图像;(2)由于采集的图片较大,需将原始图像缩小后再进行相应的处理,减小后续的处理难度;(3)通过对图像开启和闭合、二值化、边缘提取等预处理后,可求得物体倾斜角,然后将图像旋转至标准水平图;由于在旋转过程中会导致边缘部分像素丢失,因此采取了形态学膨胀和区域填充,然后再进行边缘处理;
(4)将边缘图像数值化,通过新开发的算法,求得轴的相关目标参数。
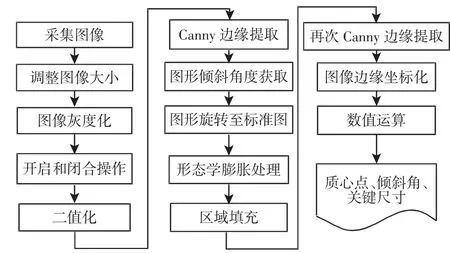
图4 算法流程Fig.4 Algorithm Flow
3.2 图形预处理算法
3.2.1 图像缩小及灰度化
通过CCD 相机采集轴的灰度图像,其像素占据大小为(2592×1944)像素,如图5(a)所示。由于图像数据量过大,不便于后续处理,因此对图像进行缩小5 倍后再进行后续处理。为了保证采集图像的完全灰度化,因此在图像缩小后,灰度图像进行再次灰度处理,处理结果,如图5(b)所示。
3.2.2 对图像进行开启和闭合
由于环境中不可避免地会存在各种噪音,对图像的质量有较大的影响;为了提高图像处理的质量,图像去除噪声必不可少。采用MATLAB 中提供的滤波算法对图形进行开启和闭合操作,实现了图像平滑和去噪,提高了图像处理效率和质量,处理结果,如图5(c)、图5(d)所示。

图5 原始图像灰度处理与滤波Fig.5 Original Image Grayscale Processing and Filtering
3.2.3 图像二值化与边缘提取
图像二值化是将灰度图像转变为黑白图像,是图像分割算法的重要组成部分。将测量的对象保留为黑色,图像背景设置为白色[10]。其原理是通过设定一个阈值,小于设定阈值则视为背景像素,反之,则视为目标像素。设原始图像为g(x,y),经过二值化后为t(x,y),阈值为P∈(0~1),具体表达式如下:

由式(3)可知,阈值作为二值化的核心参数,选择一个合适的阈值显得尤为重要,通常可通过实验验证法或自适应求取阈值。通过一系列实验,确定阈值尽可能选在(0.8~0.9)之间为宜,处理结果,如图6(a)所示。
图像经过二值分化后,需要进行图像边缘提取。由图像边缘反映目标对象的尺寸信息、定位信息以及倾斜角度信息等,而且图像边缘化后可以将大量的数据简化为目标边缘数据,可以减少占用内存和降低后续处理难度;边缘提取有较多的检测算子,如Roberts、Canny、Prewitt、Sobel 以及Log 算子等,由于Canny 算子边缘检测方法不易受噪声的干扰,能够直接检测到真正的弱边缘[4、10],在噪声的情况下,也能较好的提取边缘;因此,采用Canny 算子进行边缘检测,处理结果,如图6(b)所示。

图6 灰度图二值与边缘检测Fig.6 Grayscale Binary and Edge Detection
3.3 目标对象的定位算法
首先,轴的定位包含两个主要的参数,即倾斜角度与质心位置。通过边缘提取后,需要对边缘进行数值化,然后进行相应的数值计算;其中,获取质心的关键是将数值化后的边缘点集合转变为一个坐标集合,然后使用[y,x]=find(k5)与mean 算法求取平均值(x0,y0),具体表达式如下:

获得轴的质心后,采用MATLAB 内置算法,直接求取了轴的倾斜角度,简化了算法过程,提高了运算效率。
3.4 目标对象的尺寸测量算法
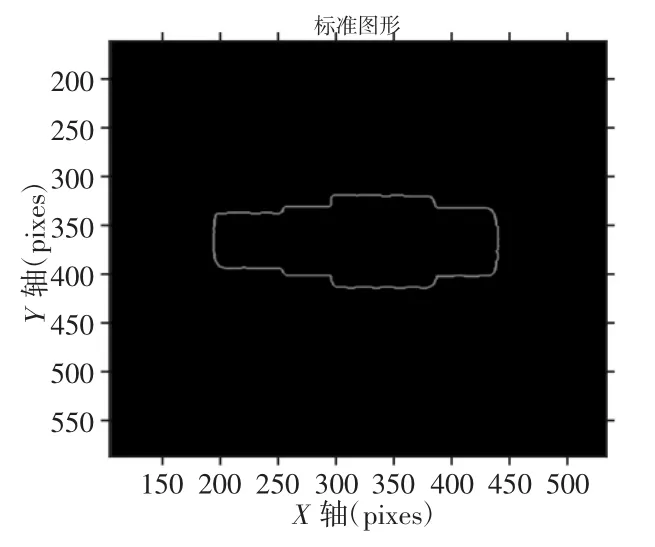
图7 水平放置标准图Fig.7 Horizontal Standard Map
经过以上的处理后,图像已经数值化,而且获取了轴的中心与倾斜角度,接下来主要是围绕求取轴的各段直径和长度,开发的算法结合倾斜角以及判别函数,巧妙地将倾斜轴图像水平放置且标准化,即经过算法处理后都会转变为统一的状态特征,解决了轴测量时任意摆放的问题,且达到图形简单化的目的,如图7所示。图形简化后,在轴的端面会出现一个x坐标值至少对应3 个相同的y坐标值的情况,称之为跳变现象,通过算法判别轴的端面处的坐标点后,并对坐标点进行提取;而且,在每一轴段只需提取相同x对应的两个y坐标值以及多个y值对应的x坐标,即可求取各段的长度与轴径。轴水平放置后,不一定是所要求的标准形状,如图8(a)、图8(b)所示。旋转后都不是标准图形,因此需要对水平的轴,进行标准模式判别,从而做出相应的调整。轴的中心一般更接近于较大直径的轴端。依据标准图像中心坐标的x′0和图像最小x之差与图像最大x和中心坐标的x′0之差m进行比较,如果判定不是标准图像,则进行旋转图形180°,即可得到标准图像。

图8 水平放置后需要调整的情况Fig.8 The Need to Adjust after Horizontal Placement
通过实验发现,旋转为标准图形后,会导致部分像素丢失,如图9(a)所示。为了填补丢失的像素点,保持图形连续性,采用了图形膨胀、填充再边缘化处理,处理结果,如图9(b)~图9(d)所示。由于膨胀后提取的边缘尺寸会相应地变动,因此在求得各像素尺寸后,还需减去相应的像素值,从而得到精确值。经过上述标准化处理后,即可进行尺寸的提取。该算法核心为循环判断,从而获取相应的目标点,由此能自动准确定位至目标过渡点,即可求得d1、d2、d3、d4及轴各段的长度尺寸L0、L1、L2、L3;最后,再乘以相应图像缩小倍数的倒数,就可以求得各尺寸的像素值,通过标定得到像素与实际尺寸之间转换关系,就可以获得实际尺寸值。
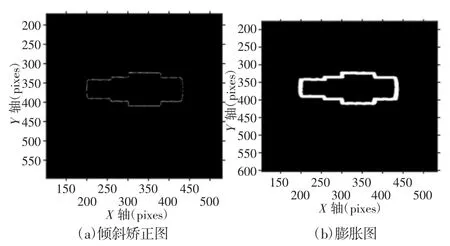

图9 边缘处理图Fig.9 Edge Processing
4 实验结果分析
4.1 结果分析
实验操作系统采用Windows7 64 位笔记本电脑,软件为MATLAB R2016b,以及直径不同的45#钢四段轴为实验对象。将四张任意放置的图片输入算法中,验证其有效性,原始图片,如图10(a)所示。处理结果,如图10(b)所示。

图10 四种不同位姿图和处理结果图Fig.10 Four Different Posture and Processing Results
为了便于观察尺寸对应关系,使用CAD 绘制二维图形,如图11(b)所示;依据生成的标定参数以及矫正[11]后的各标定后角点像素值,使用两点距离公式,求得所有标定板相邻两点之间的间距,然后求得平均值。已知标定板方格的边的尺寸为4mm,最终可求得像素与实际尺寸之间比值为16.9066piexs/mm。轴在不同位置情况下的测量结果,如表3 所示。
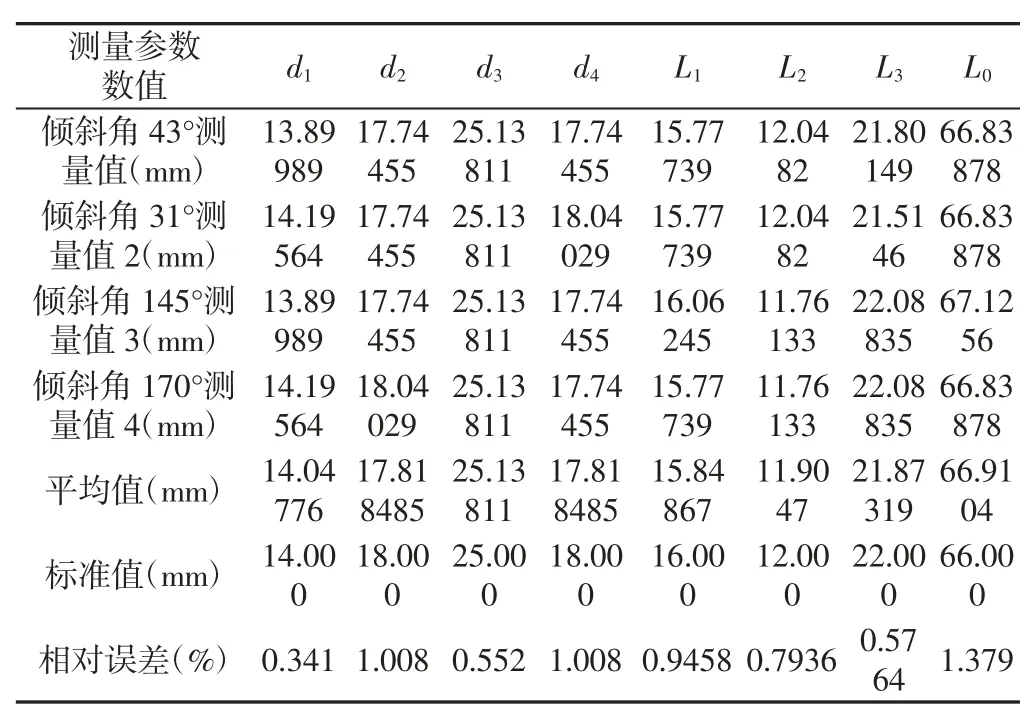
表3 实验结果与标准值的比较Tab.3 Comparison of Experimental Results with Standard Values
且进行求取结果平均值再和标准尺寸作相对误差分析;从表中可以看出,测量存在一定的误差,原因可能来源于硬件本身的精度,光源亮度调整不合适以及实验环境的影响等。为了便于客户以及研究人员的参考及使用,为此还设计了可视化界面GUI,界面,如图12 所示。GUI 界面设计执行按钮包括载入处理图片,图像预处理,获得倾斜角,获取标准水平图形,获取轴的各段长和直径,以及退出等。载入的图片以及处理后的图片都会显示在界面上,获得的参数也会显示在右侧黄色的方框中,这不仅能有效的查看图像处理过程,而且能更有效地检查是否在处理过程中出错,方便了开发系统的使用,增加了便捷度,所以GUI 设计具有必要性。

图11 目标轴的二维图形Fig.11 Two-Dimensional Graphic of the Target Axis
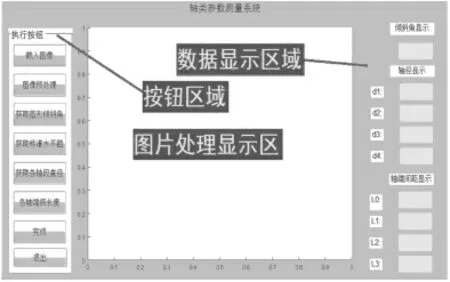
图12 GUI 界面Fig.12 GUI Design Interface
5 结论
(1)基于MATLAB 软件,开发了一套轴类零件定位与测量系统。系统实现了对轴类零件的定位以及关键尺寸的测量,同时也设计了可视化GUI 界面;
(2)介绍了CCD 相机标定和畸变校正方法,系统实现了对多段轴的中心、倾斜角度以及关键尺寸的提取。通过实验获得的平均定位误差为0.1mm,平均角度误差为1°,平均尺寸测量误差为0.2mm,验证了算法的有效性且满足工业应用要求;
(3)该测量与定位算法具有很好的延展性和可移植性,在工业中具有很大的应用价值,在保证一定精度的前提下,减轻了工人的劳动力,节省了大量的设备与人工成本;
(4)下一阶段的实验研究目标是针对复杂工况下的复杂零件的测量以及进一步提升精度,为机器视觉领域提供新的思路和研究方法。
