仓库搬运机器人导航运动控制与NURBS 轨迹规划

李 航，王朝耀

（1.长春职业技术学院，吉林 长春 130000；2.西安科技大学，陕西 西安 710054）

1 引言

随着机器人在感知和操纵方面获得越来越多的能力，相关行业领域希望机器人解决日益复杂和更高相关性的任务，机器人行为设计和组合变得更加复杂。在仓库搬运的需求中尽可能地实现自动化搬运过程，这将改善整个仓库工作的可扩展性和稳健性。在仓库搬运的过程中，开发与人密切合作的机器人的关键挑战是创建一个用户界面，允许用户快速，轻松地向机器人传达复杂的指令。我们考虑使用仓库搬运机器人实现物流的货站传递功能，该机器人设计采用轮式或履带式车辆用于将重载运送到难以到达的位置。在该应用中，用户界面的主要任务是使机器人在整个组中以正确的形式行进。介绍了反光标记和激光雷达，允许特定用户将自己指定为机器人的控制者，并沿着所需的路径引导机器人。在各种照明和运动条件下通过无约束和杂乱的仓库环境来检测和跟踪机器人。仓库搬运机器人按照传统自动控制系统的定义，系统的主要组件可分为控制器、传感器、规划器以及执行器四大部分，现代智能移动机器人摒弃了陈旧的控制系统结构，基于网络控制系统（Network Control System）来实现执行器群、传感器群以及总控系统间的数据传输以及集中控制[4]。规划系统将是开发复杂机器人行为的自然组件。

移动搬运机器人的控制系统架构：控制平台通过ECAT 总线建立硬实时环境，NCS 中提供多种硬件接口诸如：I2C、PCI-E、USB 以及RJ45 等，保障了多种传感器与控制核心的实时通讯。NCS 分为输入、输出双通道，多种传感器的反馈数据与伺服驱动电机的控制信号并行于控制网络内部[5]。搬运机器人运动的过程中，通过激光传感器完成环境中的伪定位，辅以电机位置传感器来记录机器人的里程信息，根据当前的路径、运动方向等信息，可实现最优路径的规划以及地图信息的匹配，最终实现响应迅速、控制灵活的导航。在搬运机器人行走过程中，还需要对底盘的轮子进行轨迹规划，介绍了计算NURBS 曲线和曲面偏移的算法。基本方法包括四个步骤：（1）识别特殊曲线和曲面；（2）根据二阶导数的界限对偏移曲线或曲面进行采样；（3）插入这些点；（4）使用偏移公差去除所有不需要的结点。该方法提供了对错误控制的良好处理。

2 仓储搬运机器人平台概述

2.1 仓库搬运机器人概述

仓库中，需要对很多物品进行搬运，需要把物体按类、按号、按项目进行分类搬运，工作人员厌倦了拖着沉重的材料长途跋涉。这些工人的行走距离在他们班次期间达到10km，运输任务每周发生195h。仓库进行搬运的机器人不间断进行信息的传递，从而帮助搬运工交付货物到指定的工作站。仓库搬运机器人每周7天，每天24h 工作，能够在仓库内的任何地方无人驾驶，无需人工地标，避开人们共存的障碍，6 台机器人可以节省2.8 名全职员工。

图1 仓库搬运机器人平台示意图Fig.1 Schematic Diagram of Warehouse Handling Robot Platform

搬运机器人按照以下顺序移动：（1）从基座开始，（2）到达拾取位置，（3）移动到下降位置，（4）返回到基座。有时底座和拾取位置可以处于相同位置。为交货任务分配了可用的机器人。但是，即使所有机器人都未送达，交付请求也会持续发生。如果没有最佳分配算法，则机器人一次只能执行一项任务。在这种情况下，如果所有机器人都忙，则稍后请求的交付应该等到机器人完成其任务并变得可用。这种方法很简单，使用多个机器人效率不高。该方法称为单任务分配（STA）。

因此，我们引入了一种多任务分配（MTA）方法来提高生产率。此方法为机器人分配多个任务。要为已经交付的机器人分配多个任务，必须考虑行程距离，剩余电量和最大负载能力。然后，它选择适当的机器人（当前正在交付机器人）来分配多个任务。它还具有重新规划路径与当前任务和新分配任务的关联过程。该方法将缩短拾取位置的等待时间并提高整体效率。

2.2 机器人控制仿真平台

为了评估机器人的性能，开发了一种模拟器来测试使用多个机器人进行仓库后勤的各种情况。模拟器由参数设置，任务调度器，核心和数据分析器组成。任务调度程序是用户定义的任务计划列表，包括货物类型，时间段以及提货和下车的位置。环境参数在参数设置模块中定义，该模块影响核心的模拟。核心是机器人在线运行并根据任务调度程序调用传递请求的位置。核心内的任务分配器在考虑约束的同时将新接收的任务分配给机器人。数据分析器显示交付任务的结果，包括等待时间，总交付时间以及每个机器人的已完成任务的数量。

模拟器由参数设置，任务调度程序，核心和数据分析器模块组成。在设置参数和安排交付任务之后，核心运行抽象的9 小时，其中调用交付请求并且机器人以其速度移动。模拟完成后，用户可以在数据分析器中获得模拟的性能结果。

3 机器人运动控制

3.1 双轮差动控制模型

采用双轮差动方式运动的移动机器人，其左右轮轮速分别为Vl，Vr，车体宽度为d，整车运动轨迹的圆半径为r，在Vl＜=Vr的情况下，由左右轮差速所构造的运动轨迹分析如下：

当Vl＞Vr时，情况与此相同，则公式变为趋向正负无穷的时候，车走直线，r=0 时车原地旋转，r＞0 时车体向左侧旋转，r＜0 时车体向右侧旋转。

此公式用于理想情况下的机器人运动轨迹估算，但在实际应用时，还有机器人运动左右轮转动方向的摩擦力，机器人左右轮装配加工的误差，机器人轴向受力时，机器人轴向被挤压时，机器人轴向被拉伸，只有当时，机器人轴向力会消失），机器人质量分布不均匀（导致机器人左右轮所受摩擦力不同），温湿度等因素的影响（材质摩擦系数变化），所以需要根据实际情况调整Vl和Vr的值，并非是理论给定的轮速。以上为计算码盘位姿公式，根据读取的码盘值，计算出位姿中各个成员的增量。每次对地图类中的各个数据进行更新。

3.2 多协调任务分配

交付任务包括提货位置和下车位置。通常，每个位置都是兴趣点。（POI）发生传递请求时，控制服务器中的任务分配器为请求选择适当的机器人。通常，选择基站中的备用机器人进行传送。但是，由于传送请求是连续发生的，因此可能存在没有备用机器人的情况。在这种情况下，任务分配器应决定是否等待有可用的机器人，或者选择当前正在工作的机器人并再添加一个任务。前者是单任务分配（STA），后者是多任务分配（MTA）。在MTA 中，任务分配器还应该重新计划所选机器人的路径以最小化行进距离。选定的机器人具有当前任务的POI 和需要添加新的POI。任务分配器必须关联两个POI 以找到最佳路径。这里我们只考虑了寻找最佳路径的距离。未来的工作将考虑电池和容量。

在MTA 中，通过穷举计算所有机器人从其当前位置到新添加的拾取位置的路径来选择接收新任务的机器人，如图2 所示。该一阶搜索路径是从计算从当前姿势到当前航向POI（图2（c））或新增加的拾取POI 的最短距离得出的。（图2（d））从两者中选择最短路径。然后，它再次计算距离，即从选定的一个到另一个。最终选择给出最短距离的机器人来添加新任务。然后，再次，通过穷举搜索，通过关联当前剩余任务的POI 和新添加的任务的POI来完成所选机器人的最短路径。路径应遵循下降位置不能超过拾取位置的约束。这样，MTA 选择了一个可以完成两项任务的机器人。为了测试STA 和MTA 的性能，设计了一个模拟器。它模拟仓库环境，机器人和频繁交付任务的时间表。

图2 找到选择机器人进行多任务分配的路径的方法。Fig.2 The Method of Finding Path to Select a Robot for Multi-task Allocation

3.3 导航运动控制

在（60*70）m 的地图中使用10 个机器人，具有8 个交付位置，如图所示。机器人可以接受的最大交付任务数量为2。模拟运行抽象9 小时以及每个机器人的频繁按需任务用于测试的POI，如表1 所示。每5min 调用从第7 个POI 到第1 个POI 的递送请求。从基站到第7 个POI 的持续时间约为8min，速度为1m/s。STA 和MTA 算法的性能在模拟器中进行测试。通过分配时间，等待时间和总交付时间来比较性能。分配时间是递送请求和机器人分配之间的时间。在STA 中，当存在新的递送请求时所有机器人当前正在执行任务时，机器人的分配被延迟直到机器人完成其任务。等待时间是从请求交付时间到机器人到达POI 以获取包裹的时间。总交货时间是提货和下车之间的时间。

图3 在60m*70m 的地图上有8 个POI 和10 个机器人Fig.3 There are 8 POI and 10 Robots on the 60 by 70 Meter Map

单任务分配（STA）和多任务分配（MTA）的结果，如图3 所示。蓝线是STA，红线是MTA。图中的x轴是按顺序编号的交付任务ID，y轴是等待时间（以分钟为单位）。由于其他机器人都在忙着执行已经分配好的交付任务，所以分配给STA 的机器人的等待时间随着时间的推移而增加，如图4（a）所示。同样的，STA的一次叫车后机器人到达取货的等待时间增加，而MTA 的等待时间相对较短，如图3（b）所示。

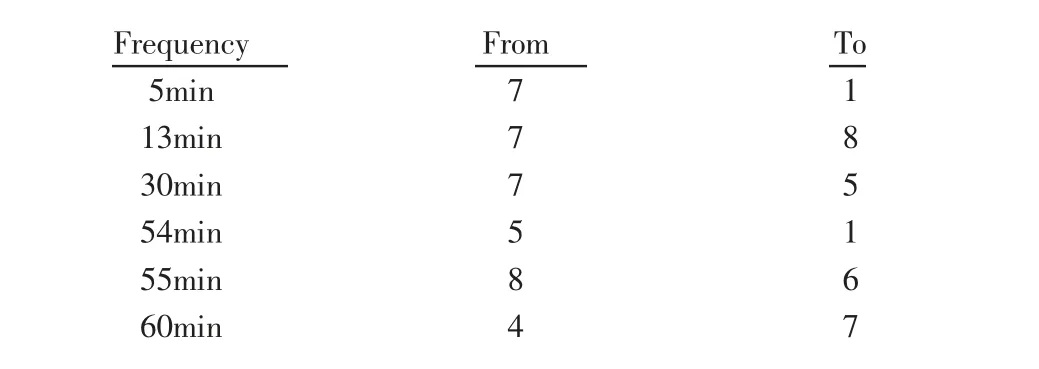
表1 交货时间表Fig.1 Delivery Schedule

4 NURBS 的轨迹规划

4.1 基于多项式的轨迹规划方法

如果要加入其他约束，比如关节起始、终止加速度的约束，就要使用5 次多项式。原理是与3 次多项式计算类似的。对于需要精确经过某些位姿点的情形，利用多项式插值就比较麻烦，且多项式的幂次也要增加，这里就不再赘述。

这里需要指出的是利用多项式进行轨迹规划的时候，有时候会将多项式写成正则的形式。正则多项式一般形式如公式所示。

式中：T—轨迹规划时间；t—机械手运行时间。

新松公司的6 自由度机器人多用多项式经行轨迹规划，利用七次多项式插值得到的机器人轮子的轨迹规划曲线，下面是按七次多项式插值的关节运动轨迹曲线，如图4（b）、图4（c）所示。这组速度和加速度曲线是在图4（a）轨迹的基础上得到的。但真空机械手需要经过多个中间位姿，多项式规划就不太实用了。

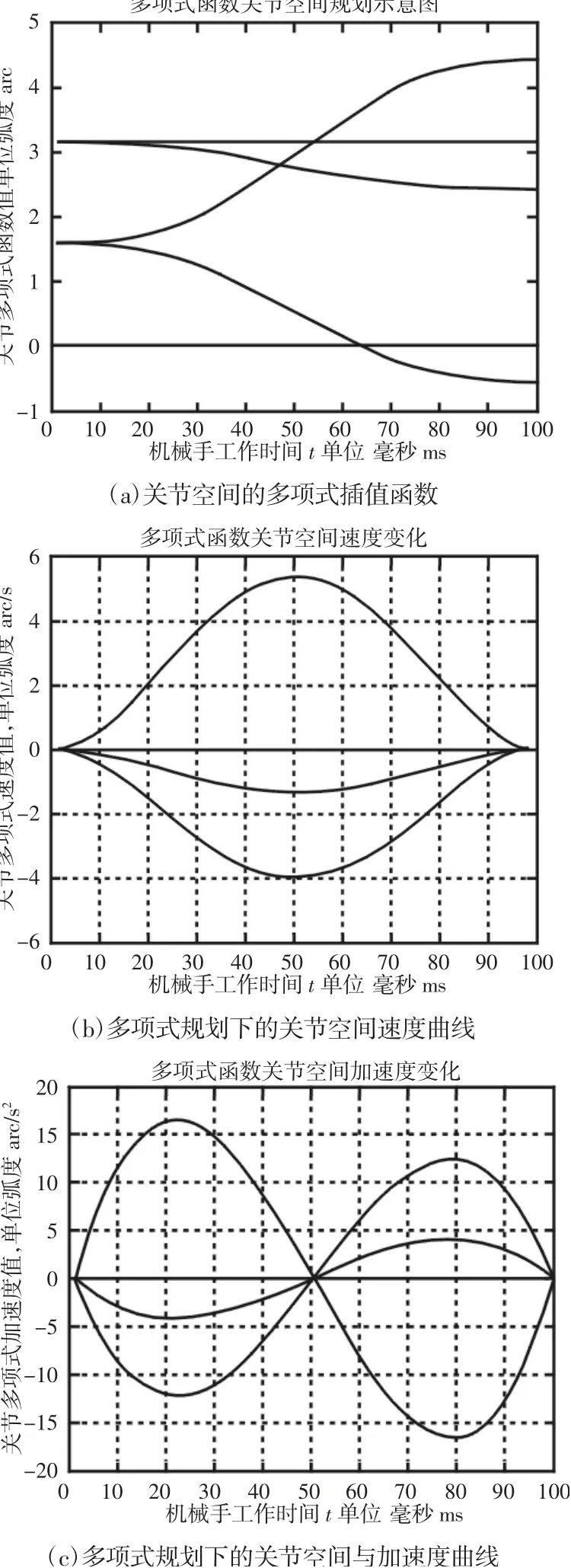
图4 关节运动轨迹曲线图Fig.4 Curve of Joint Motion Track

4.2 基于NURBS 的轨迹规划方法

利用非均匀有理b样条生成的基函数构造精确的几何模型，几何分析是一种基于表示几何的函数的计算力学技术。其思想是建立一个几何模型，而不是建立一个近似几何的有限元模型，而是在分析中直接使用描述几何的函数。这意味着与有限元方法相比，自适应网格细化技术可以在不连接CAD（计算机辅助设计）数据库的情况下使用。这似乎是一个明显的优势，等几何分析超过有限元分析。此外，在每个自由度的基础上，等几何分析与有限元分析相比具有更高的精度和鲁棒性。

因为B样条曲线的每个控制点的作用域是有限的，我们将整个参数域用knot 划分成多个小的区域，在每个区域中，只有一部分不为空；我们令U为m+1 个按非降顺序组成的数字集合，U=｛U0，U1，…，Um｝，U0＜=U1＜=…＜=Um，其中Ui称为knot，U称为knot vector，每个B样条有一个degreep，这个degree 决定了N（u）受几个控制点影响（p+1 个），B样条的basis 函数的递归定义为公式，即Cox-de Boor 递归方程。

NURBS 曲线轨迹的矩阵计算法及矩阵表示。若曲线采用三次NURBS 形式表示（三次与K次计算方法相同，只是表达式有所不同），则我们可以将第i段曲线可以写成下列矩阵形式，如公式所示，t∈［0，1］，i=3，4…n：

整理可得，公式，t∈［0，1］，i=3，4…n：

由于控制点pi及权因子ri均已知，而Mi仅与节点向量有关，也是确定的，Ci与Mi、ri、pi有关，即也是确定的。对于曲线上坐标X、Y、Z分别有公式，t∈［0，1］，i=3，4…n：

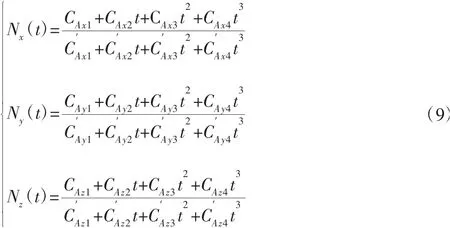
5 实验验证

5.1 多机协调实验

为了测试STA 和MTA 算法的性能，我们开发了一个实现仓库环境和机器人的模拟器。当模拟器运行时，任务分配器分配机器人以执行传递任务，并且机器人通过自主规划路径移动到地图内的传递位置。参照仓库搬运机器人所处的环境地图以及交付物品时间表，搬运管理层可以决定在仓库部署多少机器人以满足所需的交付绩效。在多机协调任务分配过程进行测试，调度多任务进行搬运任务时，如图5 所示。搬运机器人相互直接如果发生碰撞，采用最优控制来决定那台机器人继续执行，另外一台采用避让的策略。分配的总体结果，如表2 所示。在给定的仿真时间内，MTA 的完成任务数大于STA，为104.67%，等待时间显著减少，为32.96%。

图5 搬运机器人多机协调Fig.5 Handling Robots Coordinate with Each Other

表2 分配任务的结果Fig.2 The Result of Assigning Tasks

5.2 避障实验

对搬运机器人进行行走避障的测试，如图6（a）、图6（b）所示。搬运机器人避障依靠激光，激光采集周围环境信息，发现必经的路程中有障碍物，从旁边饶过去，继续行走。

图6 搬运机器人行走避障Fig.6 Carrying Robot Walks on the Barrier

5.3 NURBS 实验

对搬运机器人它既能帮助渡过运动不确定位置，又能增加最大启动牵引，搬运机器人的运动要求确定。图3～图7 是路径规划方案的示意图。这里选取N=3 和N=10，规划达到4-5-6-7 正则多项式的路径规划效果的实验图，如图7（a）～图7（d）所示。x=t/T，其中，T为路径规划的时间，p（x）表示4-5-6-7 正则多项式的取值，从仿真图可以看出误差e（x）=s（x）-p（x）及其一阶、二阶导数都在可以接受的范围。

图7 多项式路径规划效果实验图Fig.7 Experimental Diagram of Polynomial Path Planning Effect

从图中，我们可以看到每增加一次求导，误差也会增加一个量级，一般加速度误差会比位移误差高两个数量级，这在实际设计中是不能忽略的。

6 结论

仓库内部提供了许多不同的材料，并引入了自主导航移动机器人来取代这种重型移动工作。

（1）首先，详细的介绍了仓库搬运机器人的概念和机器人的控制仿真平台。

（2）其次，对机器人的双轮差动控制和多任务协调分配进行了研究，（STA）不是使用机器人一次传送一个包，而是可以将多个任务分配给机器人（MTA）以提高使用多个机器人的效率。因此，引入任务分配算法以实现多机器人—多任务分配。

（3）再次，对机器人如何能够在仓库搬运中找到目标位置，提出了导航运动控制方案。

（4）最后，提出了一种NURBS 算法，该方法依赖于基于导数，插值和结去除的点采样。几乎所有先前的方法都以几个段开始，并添加点直到近似收敛。

实验表明，与使用相同数量的机器人时的单任务分配相比，MTA 的效率显着提高。并且机器人能够在无人的环境下精确导航，把物体移动到目标位置点。同时大量的采样点可以产生相当好的参数化插值曲线，这反过来又可以消除很多结点。使得搬运机器人能够平稳导航运行，以便保持误差并且参数化表现良好。