多源不确定条件下的M 公司生产线优化研究

2020-07-22杜嘉玮王少华

机械设计与制造 2020年7期

杜嘉玮，王少华，梁箫

（西南交通大学机械工程学院，四川成都 610031）

1 引言

生产线优化问题是工业工程领域的重要问题。研究如何使用合理的优化方法优化生产线，使生产线高效稳定，提高产出效率，对提高生产系统稳定性和不断挖掘生产系统潜力有着重要意义。

生产线优化主要涵盖的方向有：生产线布局优化，生产线平衡优化，缓冲暂存区设置等。文献[1]使用Petri 网对飞机装配线进行建模并使用Em-Plant 仿真软件对模型进行生产线平衡，布局上的优化。文献[2]使用价值流图分析的方法对某工厂发动机生产线进行了优化。文献[3]同样基于价值流图，对某工厂抽油杆制造流程进行了优化。文献[4]使用多种群遗传算法对生产线平衡问题进行了研究。文献[5]考虑了零件选取和人机工程风险双目标下的生产线平衡设计问题。文献[6]使用ECRS 原则等工业工程方法对某电机生产线进行了平衡研究与优化。

暂存区设置和暂存区的容量设计一直以来是研究的热点。文献[7]提出了一种基于可用度评价的生产线缓存分配方法。文献[8]考虑了加工设备加工时间的随机波动性，并使用线性规划方法求解暂存区的最优库存量。

但上述文献中，都没有将生产线优化和暂存区设计联系起来。这是因为上述文献研究的生产线优化问题都是静态的，没有考虑加工时间的波动等动产线优化方法难以在实际态问题，也就不用设计暂存区来平衡生产线的波动。但是在实际生产过程中，不存在静态的生产线，加工时间的波动随时发生。这就意味着基于静态的生生产过程中取得理论上的效果。

针对上述问题，结合M 公司实例，提出了在加工时间波动的动态条件下，使用Em-plant 仿真的方法，对生产线进行深入分析和改善。包括识别瓶颈工序，提高生产线平衡率，提高产量和平准化水平，优化布局，并对生产线的暂存区容量问题进行了研究。

2 企业现状分析

M 公司是一家为国内某著名汽车主机厂供应后视镜的企业。其产品包括6 款车型后视镜，总计约40 余种型号。其产品具有型号多，但加工过程较为类似的特征。

面对主机厂和汽车生产行业对供应商准时化要求的不断提高，以及汽车零部件供应商之间的日趋激烈的竞争，M 公司急需提高自己的准时化供应水平，缩短生产周期，快速反应能力，以提高产量，实现生产线平衡，并最终提高整个供应链的稳定性。

2.1 生产线平衡与平准化

过去的研究通常是采用秒表测时法对典型产品的各生产流程进行测时，汇总得到工位信息表。此方法对于单品种产品的生产是可行的，但是，对于多品种小批量生产，此种方法会错误估计生产线平衡水平。多种产品的工位信息表应该考虑不同产品的配比关系，如表1 所示。

表1 工位信息表Tab.1 Location Information Table

表中，产品配比是指该厂三种主要产品型号的产量比，即A：B：C=5：3：2。预估时间为A，B，C三种产品的加工时间。合计时间为三者的加权平均，以工位1 为例，总时间为T=25*0.5+32*0.3+27*0.2=27.5。

式中：n—工位数：Ts—瓶颈工序时间；Ti—每道工序时间。将数据

带入得到结果，如表2 所示。

表2 生产平衡表Tab.2 Balancing Rate Table

当使用A 或C 的生产信息计算生产线平衡率时，误差都较大，不能在长期取得较好的优化效果。加权后，得到生产线平均平衡率为84.65%。平均生产节拍为30.3s/件。平均客户需求700 件/天，有效工作时间400min，即24000s。根据历史数据客户平均需求节拍为34.3s/件。各产品生产节拍和平均生产节拍都小于客户需求节拍，满足需求，但生产资源配置偏大11.67%。

平准化生产是指在能够完成计划任务的前提下使生产资源波动尽量小的排产方式。M 公司现行的生产计划甘特图，如图1所示。

图1 生产计划甘特图Fig.1 The Gantt Chart of Production Planning

可见M 公司采用日集中生产的策略，EPEI（完成一次所有种类产品的生产时间）完成一次所有种类产品的生产时间需要364Min，在生产开始的175Mins 内不能提供B，C产品，生产开始的287Mins 内不能提供C产品。三个阶段生产资源配置按照每种产品加工总时间计算，浪费比率设为最大加工时间与其余工作加工时间之差占总加工时间之比，计算得比率为5.4%。

2.2 生产布局

M 公司为了满足生产要求，灵活配置生产资源，选用单元生产线进行生产。单元生产现在是面对多品种小批量环境，最有效最灵活的生产组织方式。但是，由于M 公司的单元生产线布置不够科学合理，导致生产单元存在占地面积过大，物料供应不够顺畅，在制品过多等问题。现在M 公司的生产单元平面布局图，如图2 所示。

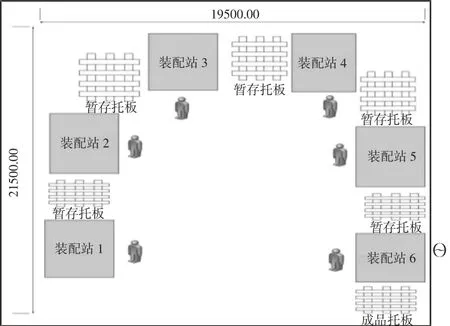
图2 平面布置图Fig.2 Layout Figure

经测算，整个生产单元长19.5 英尺，宽21.5 英尺（1 英尺约为0.3m），面积总计419 平方英尺。装配站之间除了暂存区之外还存在传送带，为了图示清晰没有画出。

2.3 生产线波动分析

生产线波动主要包括机器故障和加工时间波动，这二者都会造成产量的波动。使用Em-Plant 软件，建立生产线的仿真模型，对机器故障和加工时间波动对产量的影响进行分析研究。

Em-Plant 是物流系统，离散制造系统等常常采用的仿真软件。该软件由西门子PLM 部门研发，并面向包括西门子子公司在内的全世界发售。该软件基于C++开发，是面向对象的仿真软件，具有便于使用和便于构建大型仿真系统的能力。

将各工站的Protime 设定为2.1 中计算得的加工时间，并建立模型，如图3 所示。

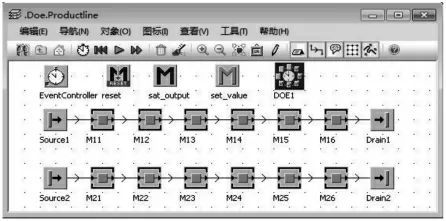
图3 生产线仿真模型Fig.3 Manufacturing Line Simulation Model

Drain1 表示不考虑机器故障和加工时间波动时的生产线。根据生产线的历史数据，设置Drain2 的Availability 参数为96，表示每100h 会有4h 的故障时间；MTTR 设置为720 表示平均修复时间为720s；全局参数Sigma 为3，即加工时间标准差为加工时间的3%。

设定仿真时间240h，得到仿真结果，如表3 所示。

表3 仿真结果Tab.3 Result of Simulation

在装配站可靠度为96%，平均修复时间为720s，加工时间符合均值为平均加工时间，标准差为Sigma 的正态分布时，生产率下降16.69%，如表3 所示。

3 设计与优化方案

3.1 生产线平衡优化

同步化生产能有效提高生产的平准化水平。所谓同步化生产是指每日按定量生产各种类型的产品，通过不断循环来达成日生产计划。根据需求的实际情况，将循环次数定为三次并绘制甘特图，如图4 所示。均衡化后，EPEI 下降为121mins，能更敏捷地应对插单等需求的动态变化。同时，生产资源配置也得到优化，浪费比率下降为1.8%。

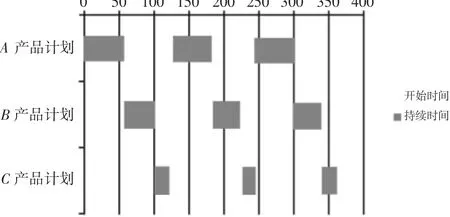
图4 改进甘特图Fig.4 The Gantt Chart of Improvement

根据ECRS 原则和实际情况中不能改变工位数和人员数的约束，以最大化生产线平衡率，对作业进行改善压缩，分担转移和合并重排。通过将瓶颈工位4 的第一道工序分配给工位3，同时将工位3 的第一道工序分配给工位2，此时瓶颈工位成为工位5，瓶颈时间为26s，此时的生产线平衡率经计算为98.5%。

3.2 生产布局优化

在传统布局优化中，一般使用考虑物流强度和交互影响的SLP 方法，但优化生产单元内部一般采用简单规则的优化方法，即通过一些简单的，经过实践检验的规则来优化生产单元内部的布局。目标是在不改变工站数量和面积的情况下，最小化单元生产线的占地面积。

这些规则主要包括：拐角处生产单元应该斜角布置以节约空间；通过提高生产线平衡率减少在制品存储规模；工件或物料采用斜槽物料架从外部送入；单元生产线应该首尾相接，增大灵活性。改进后平面布置图，如图5 所示。

图5 新平面布置图Fig.5 New Layout Figure

通过在装配站之间添加滑槽物料架，根据改进后的生产线平衡率调整暂存区大小，通过改变装配站3，4，6 位置的方法，使改进后单元生产线长14 英尺，宽18.5 英尺，面积变为259 英尺，比优化前占地面积减少38.2%。

3.3 暂存区分析优化

暂存区可以减少由于生产线的波动而造成的生产线产能损失，这是因为一旦生产线中的某一个单元出现故障或者加工时间出现波动时，下一生产单元可以接受暂存区的零部件，而不用等待上一单元恢复正常。

但是在实际生产过程中，暂存区的容量并不是无限大，并且盲目增大暂存区容量并不一定能增加生产线产出率。在何处设置暂存区，暂存区容量设置为多少都需要考虑。

首先建立暂存区设置的数学模型。在考虑产线可靠性约束的情况下，优化产线最大产量。

可靠性的参数表示为机器故障的最大修复时间，在最大修复时间内如果缓冲库存可以满足后续生产的需要，即该生产线可靠。

根据机械设备可靠性原理，一般设故障设备最大维修时间符合对数正态分布，则有：

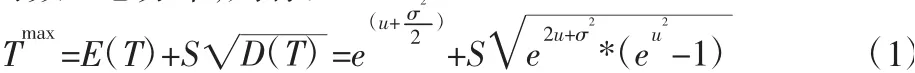
式中：u—故障设备维修时间对数均值；σ—故障设备维修时间对数方差；S—置信系数，在该模型中即为可靠性程度。根据查表可知，S符合如下关系。

在某个可靠性约束下，可以得到故障设备在该可靠性要求下的最大修复时间，进而可以依据下式：将可靠性约束转变为暂存区最小库存量约束。

式中：BFi—第i个暂存区零部件数量；Wi—第i个机器的生产率。

上式表示若暂存区零部件数目大于该机器故障最大修复时间内生产线的需求数，则该生产线可靠性约束满足。

由式（1）和式（2）得到的最小安全库存为：

要求生产可靠性99%，设备维修时间服从对数正态分布LN（3.0，0.2）。生产率即为生产节拍，即u=3.41，σ=0.6，S=2.33，w=30.3s。将参数带入式（3）可以得到最小安全暂存区库存约为6 件。

计算机仿真是解决这个问题的有效方法，仿真模型的基础，加入实验设计器，研究暂存区设置问题。

在各工站间设定暂存区Buffer，设为Buffer1 到Buffer6。实验类型为多因子多水平实验，各暂存区容量从2 到10 变化，级差设置为2。实验观测次数设定为1，置信区间设定为95%。共需进行15625 次实验仿真。仿真运行3.35 小时，得到仿真结果，如图6所示。对实验结果进行分析。根据99%可靠性和暂存区最小零部件数量为6 的约束，并且根据生产率最大和暂存区库存总量最小的优化目标对实验数据进行筛选，得到最优配比，如表4 所示。

图6 多水平实验结果Fig.6 The Result of MLED

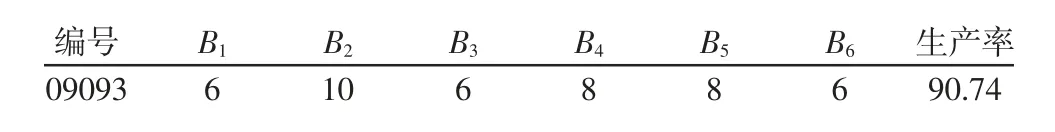
表4 最优配比表Tab.4 Table of Best Matching

4 总结

以M 公司实际生产线为例，全面调查了M 公司的实际生产情况，了解实际中精益生产面临的问题。根据多品种小批量生产的实际要求，提出了依据不同产品的配比识别瓶颈工序，计算生产线平衡率的方法。并依据ECRS 原则和人员，工位固定的约束进行优化。结果表明，根据产品配比的生产线平衡计算方法更贴近实际，通过工位间工序调整，使生产线平衡率提高了13.85%。

为提高生产线平准化水平，提出了最小化生产资料配置的优化目标，通过将日循环次数增加3 次的方法使生产资料浪费比率降低66.7%。

为在不减少工位面积的情况下最小化单元生产线面积，提出了基于规则的单元生产线优化方法，结果表明通过简单的优化规则，增加滑槽货架等方式，减少了38.2%的占地面积。

生产线设备的加工时间波动和机械故障是生产线的固有属性。通过em-plant 仿真研究了生产线波动对产量的影响。考虑设置暂存区平衡机器故障波动的方法，建立了可靠性约束下，设备故障最大修复时间符合对数正态分布的数学模型，并将可靠性约束转化为最小暂存区库存约束。在该模型的基础上，建立emplant 仿真模型。研究结果表明，在99%可靠性的要求下，最低暂存区库存总量为44，生产率较不使用暂存区增加7.41%。优化效果总结，如表5 所示。