发动机主动悬置LQG 权值优化时滞补偿控制

潘公宇，陈玉瑶

（江苏大学汽车与交通工程学院，江苏 镇江 212013）

1 引言

随着高速公路的发展，车速的提高，人们对于汽车乘坐舒适性提出了更高的要求，而发动机作为汽车的动力源所引发的振动越来越被人们所关注。传统的发动机被动悬置已无法满足人们的要求，而主动悬置由于其动态范围宽，响应速度快，功耗低已成为当前研究的热点。其系统主要是由作动器，传感器和控制单元构成，通过传感器检测发动机振动的信号传到控制器，控制器控制作动器产生主动控制力[1-2]。如果中间某些环节的响应时间较长，系统就会产生时滞。时滞对主动悬置的影响很大，会出现主动控制力与发动机运动状态不合拍，严重影响车辆振动性能。目前关于时滞补偿控制的研究大多集中在模糊控制或者滑模控制范围内，模糊控制设计尚缺乏系统性以及滑模控制的抖动问题，使得复杂系统的控制难以奏效[3-4]。而建立了发动机三自由度主动悬置模型，通过变换表达，将泰勒级数整合到LQG 控制器设计TLQG 控制器，解决了由于LQG 控制与泰勒级数直接无法结合的问题，从而解决了发动机主动悬置的时滞问题，通过仿真表明可以改善发动机隔振性能。

2 压电作动器主动悬置模型

2.1 压电作动器特性及压电方程

压电陶瓷作动器是压电陶瓷在实际应用中的一个重要领域，主要原理是利用压电陶瓷的逆压电效应。作动器是发动机主动悬置的核心组成部分，作动器的性能在一定程度上决定了主动悬置系统的隔振性能。因此选择合适的作动器是设计主动悬置的关键环节，而具有较好机电耦合特性的压电作动器，正适合应用在主动控制系统中。厚型压电作动器是由几十个甚至上百个堆叠在一起的薄型压电陶瓷作动器基于力学上的串联组成的[5]，如图1 所示。

图1 压电堆示意图Fig.1 Piezoelectric Stack Diagram

根据压电陶瓷的力学特性可以得到压电陶瓷的输出变形和输出力方程[6]如下

式（1）反映了某一压电作动器加载电压，作动反力和驱动位移三者之间的理论关系。

2.2 压电陶瓷作动器的实验研究

前文对压电陶瓷作动器进行的理论分析不能验证压电陶瓷作动器在实际使用中的特性，同时压电陶瓷作动器的使用参数也不能通过理论来得到。因此，建立了压电作动器的实验台，通过一系列的实验来探索压电作动器的特性。本试验在江苏大学力学院实验室的支持帮助下完成的，实验中使用的实验设备有实验台架、用来给压电陶瓷作动器提供电压的电源、力传感器、位移传感器、数据采集器以及分析系统。

图2 压电作动器实验台架Fig.2 Experim Ental Bench of Piezoelectric Actuator

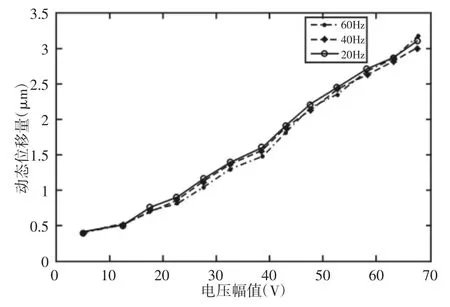
图3 压电陶瓷作动器动态输出位移Fig.3 Dynamic Output Displacement of Piezoceramic Actuator

图4 压电陶瓷作动器动态输出力Fig.4 Dynamic Output Force of Piezoceramic Actuator

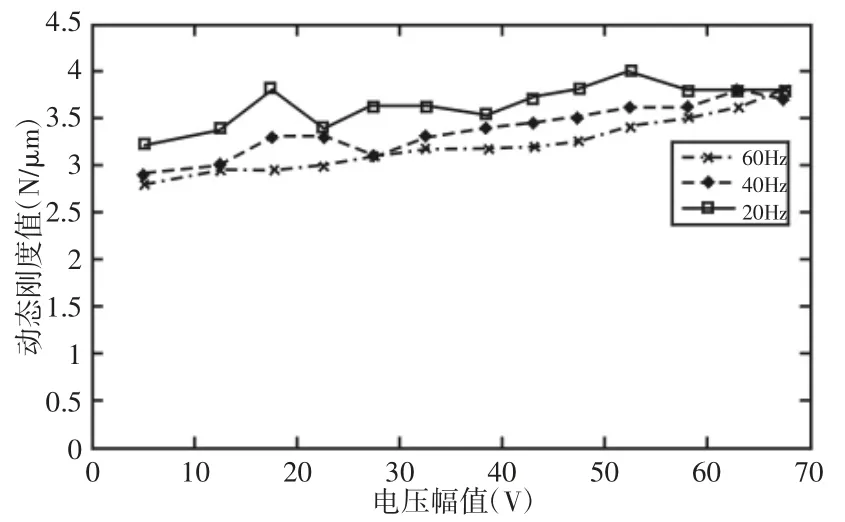
图5 压电陶瓷作动器等效动刚度Fig.5 Equivalent Dynamic Stiffness of Piezoceramic Actuator

从上图压电陶瓷作动器的实验可以看出输出力，动态位移量与电压基本成线性关系，通过实验数据的拟合，可以写出压电陶瓷作动反力与电压的关系：

同时作动器的刚度随着施加电压频率的变化而产生微小的变化，可以认为频率对刚度的影响不大，在主动控制时，可以将作动器刚度当成一个定值[7]。在控制器求出悬置系统所需的主动控制力FMR（t）之后，根据式中的FMR（t）和U（t）的关系计算系统所需的控制电压，从而对主动悬置进行控制。

2.3 发动机时滞主动悬置模型

由于信号处理所带来的时滞极小，只考虑压电陶瓷作动器响应所带来的时滞，建立3 自由度主动悬置模型，如图6 所示。

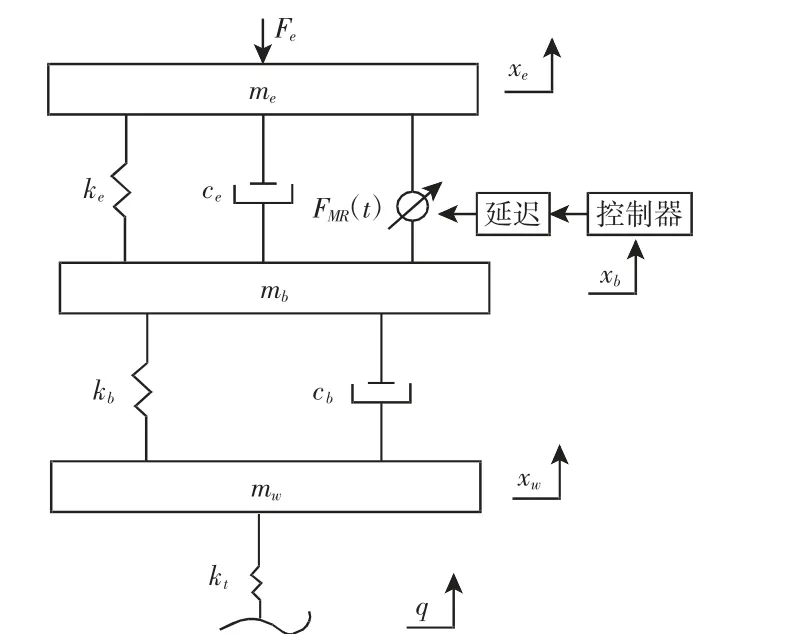
图6 三自由度主动悬置时滞系统模型Fig.6 Model of Active Suspension System with Three Degrees of Freedom

图中：xe—发动机位移；xb—车身的位移；xw—轮胎的位移；me—发动机等效质量；mb—车身的等效质量；mw—发动机等效质量；ke—主动悬置等效刚度；ce—主动悬置等效阻尼；FMR—悬置主动控制力；kb—悬架等效刚度；cb—悬架等效阻尼；kt—轮胎等效刚度；Fe—发动机激振力；q—路面不平度输入。

3 自由度发动机主动悬置模型的动力学方程为：

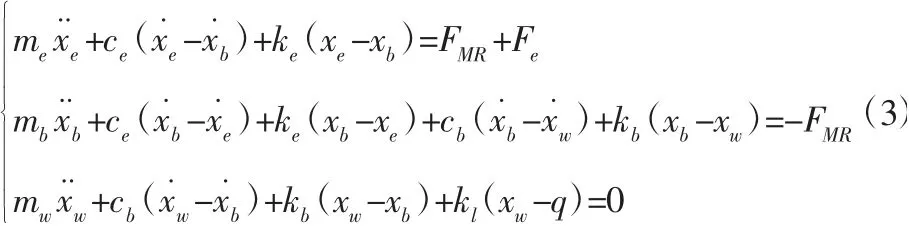
定义状态矢量：

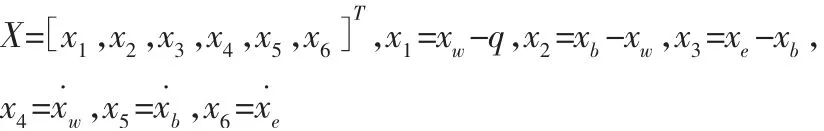
式中

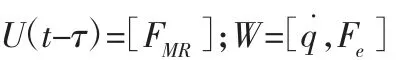
3 基于遗传算法LQG 控制器的设计

3.1 LQG 最优控制器的设计

在发动机主动悬置LQG 控制器设计过程中，发动机振动加速度，悬置的动行程，悬架的动挠度，轮胎的动载荷是需要综合考虑的四个性能指标[8]，在此利用加权系数综合考虑上述4 个性能指标，确定悬置的综合性能如下：

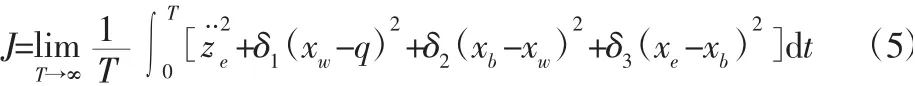
根据最优控制理论和主动悬置微分方程可以写成标准二次型：

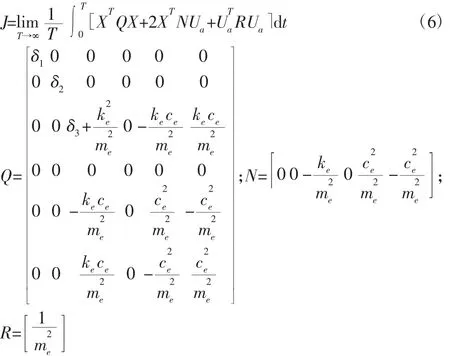
利用Matlab 软件提供的LQR 函数可以求得最优反馈增益矩阵K，表达式如下：

式中：S、E—黎卡提方程的解以及系统的特征值向量。根据LQG

最优控制理论，由下面表达式求出理想主动控制力。

3.2 基于遗传算法加权系数的设计

采用发动机主动悬置的性能指标悬置动行程（xe-xb）2，悬架动挠度（xb-xw）2，轮胎的动载荷（xw-q）2，构建用于遗传算法的适应度函数，可以构建下列形式的适应度函数。

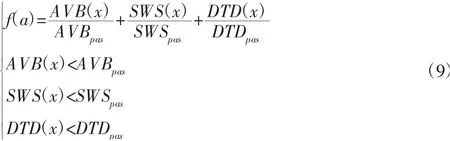
式中：AVB（x），SWB（x），DTD（x）—发动机悬置系统中的轮胎动载荷，悬架动挠度，以及悬置动行程的均方根值。AVBpas，SWBpas，DTDpas—对应被动时相应的性能。优化变量δ=［δ1，δ2，δ3］，采用遗传算法搜索加权系数δ1，δ2，δ3步骤如下：

（1）遗传算法产生加权系数初始种群，LQG 控制器加权系数δ1，δ2，δ3共三个变量，故个体表达式为δ=［δ1，δ2，δ3］使用实数编码的形式，加权系数在初始种群内随机产生。

（2）将初始种群个体依次赋值给LQG 控制器加权系数δ1，δ2，δ3，由式（7）求出LQG 控制反馈增益矩阵K，通过求解式（8）获取作动器最优控制力u，将其代入主动悬置模型中，通过控制仿真可以获得主动悬置性能指标AVB（x），SWS（x），DTD（x）。

（3）根据式（9）得出种群个体的适应度值，并且将适应度函数的极小值作为终止条件，若满足条件，退出程序并输出最优个体值，如不满足，转至（4）。

（4）通过遗传算法中选择，交叉，变异等操作实现保留精英个体和产生种群新个体，运算过程转入（2）[9]。

利用MATLAB/Simulink 软件，并借助软件中遗传算法优化工具箱进行优化搜索计算，最终获得最优个体：

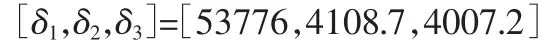
4 泰勒级数结合LQG 控制器时滞补偿控制

4.1 泰勒级数结合LQG 控制产生的预估力

由于主动隔振时滞的存在，压电陶瓷作动器需要经过一定的时间才能对输入做出响应，这会降低控制的实时性，从而恶化系统的性能。在时滞补偿控制系统中，我们考虑利用泰勒级数的预估功能，并结合LQG 控制，对系统的控制力进行预估，进而起到时滞补偿的作用。

泰勒级数仅在时滞较小时才具有较好的预估作用，压电陶瓷作动器由于其响应快，反应时间短，上海交通大学对压电陶瓷作动器时滞反馈控制进行实验研究，时滞大约20ms 左右[10-11]，所以用泰勒级数对系统进行时滞补偿控制是合理的。

在t时刻，利用泰勒级数结合传统的LQG 控制提前预测出t+τ 时刻的主动控制力Fp（t），以此对系统进行时滞补偿。Fp（t）的表达式如下：

为了分析该问题，给出了τ=20ms 时理想主动控制力Fa（t）和预估力Fp（t）之间的比较图，如图7 所示。图7 中，LQGT1 表示1 阶泰勒级数得到的预估力；ILQG 代表利用理想LQG 控制（即时滞为零的无措施LQG 控制）求得的主动力。

利用泰勒级数对控制力进行预测时，一阶泰勒级数对于理想的控制力有放大作用，如图7 所示。因此用一阶泰勒级数进行控制力的预测，故将式（10）改为：

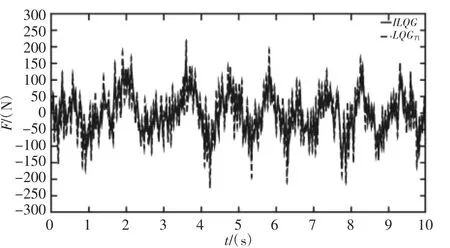
图7 一阶数泰勒级数预估力比较图Fig.7 Comparison Diagram of First Order Taylor Series Prediction Force

4.2 LQG 结合泰勒级数TLQG 控制器的设计

在式（11）的基础上，对式（4）进行扩展得到扩展状态方程如下：

相应的悬置二次型性能指标J为：

其中，N1=［0 0 0 0 0 0 0］T；R1=［0］

由于R1=0；LQG 控制器无法设计；故要对方程（14）中Fa（t）进行变换；

为满足R1＞0，对式（11）中Fa（t）进行如下变换：

经过变换后，新的扩展状态方程和二次型性能指标的表达式分别如下：

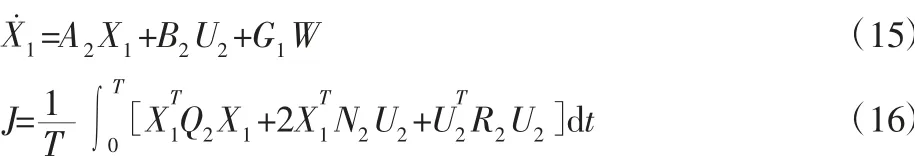
其中，U2=［Fp（t）］；

由于β＞＞α＞0，因此变换前的Fa（t）和变换后的βFa（t）+αFp（t）几乎相等，从而基本不改变原系统的动力学特性。

由于R2＞0，满足LQG 控制器设计条件，因此可以将泰勒级数与LQG 控制器结合设计TLQG 控制器。

发动机主动悬置的TLQG 控制器框图，如图8 所示。

图中的扩展方程为：

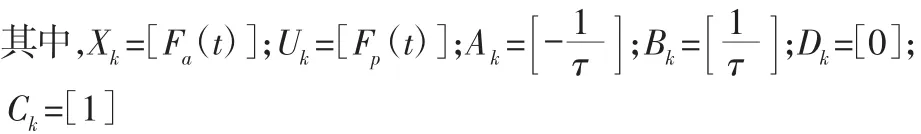
方程（17）的作用是为了将泰勒级数与主动悬置系统状态方程整合成扩展状态方程来设计TLQG 控制器。

TLQG 控制器主动控制力的输出为：

式中：K2—最优反馈增益矩阵，可以通过下式求得：

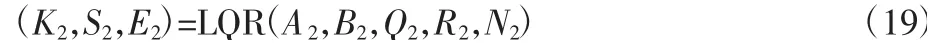
式中：S2—黎卡提方程的解；

E2—系统的特征值向量。

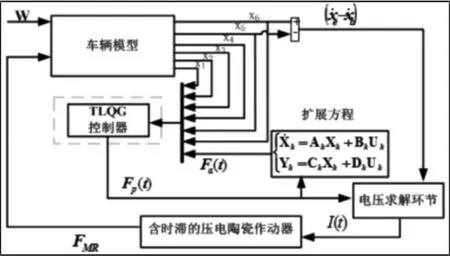
图8 主动悬置TLQG 控制图Fig.8 TLQG Control Chart of Active Mount

5 系统仿真

5.1 随机路面输入仿真

在Simulink 建模环境下模拟B级路面，输入为滤波白噪声，车辆速度为72km/h，路面不平度系数为64×10-6m3，下截止频率为0.1Hz，路面仿真图，如图9 所示。

图9 B 级路面不平度输入Fig.9 Road Roughness Input at Grade B

5.2 发动机悬置时滞仿真模型及分析

时滞τ=20ms 采用LQG 控制主动、时滞τ=20ms 采用LQG时滞补偿的主动悬置示意图，如图10、图11 所示。

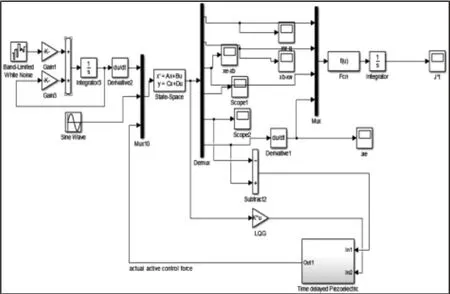
图10 时滞τ=20ms 采用LQG 控制主动Fig.10 Time Delay τ=20ms，Active Mount with LQG Control

图11 时滞τ=20ms 采用LQG 时滞补偿的主动悬置Fig.11 Time Delay τ=20ms，Active Mount with TLQG Control

5.3 仿真结果分析

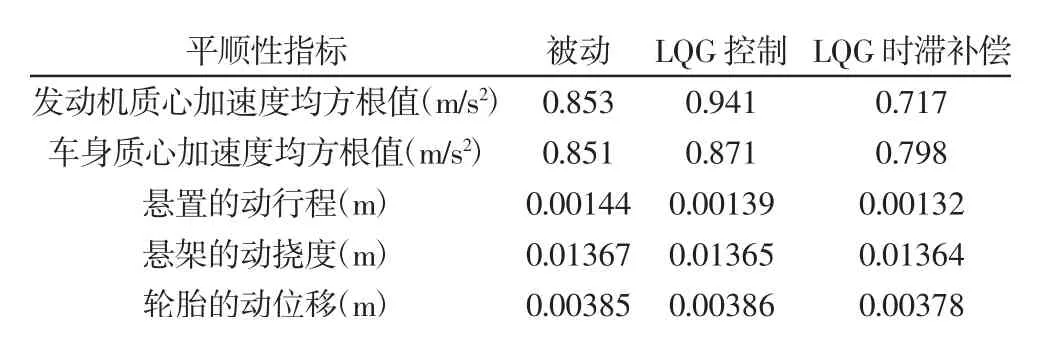
表1 时滞为20ms 时仿真结果Tab.1 Simulation Results when the Time Delay is 20ms

为了比较结果，分别计算出各项 性能指标在时滞τ=20ms时，车身的质心加速度；发动机的质心加速度；悬架的动挠度；悬置的动行程；轮胎的动位移均方根值等参数。并列表，如表（1）所示。由表可知，在时滞为20mms 时，传统LQG 控制在发动机质心加速度，车身质心加速度与被动悬置相比反而分别增大了10.3%，2.3%，这并不利于车辆平顺性的改善。采用LQG 结合泰勒级数时滞补偿的TLQG 控制，与被动悬置相比，发动机的质心加速度，车身的质心加速度，悬置的动行程等参数分别降低了15.8%，6.2%，8.3%，而悬架的动挠度，轮胎动载荷相比之下却能基本保持不变。说明所设计的TLQG 控制器对于提高车辆的平顺性有一定的作用。

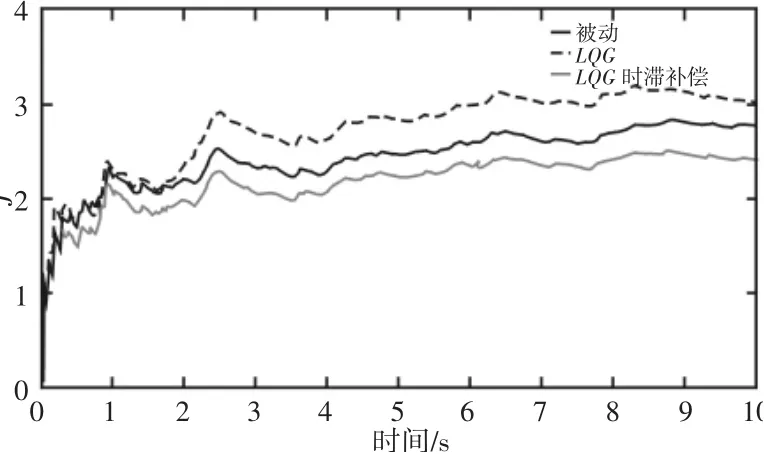
图12 磁流变时滞τ=20ms 悬置综合性能评价指标JFig.12 Time Delay τ=20ms，Comprehensive Performance J

由图12 的仿真结果，相对于被动悬置，时滞为20mms 时，LQG 控制悬置的综合性能不如被动悬置，而对于LQG 时滞补偿的悬置综合性能好于被动悬置，这也验证了仿真的正确性。

6 结论

（1）研究了压电陶瓷力学特性，通过实验近似建立了主动控制力与电压的关系。

（2）建立三自由度发动机主动悬置模型，考虑系统时滞并建立其动力学方程。通过变换将泰勒级数与LQG 控制器结合设计TLQG 控制器，为发动机时滞补偿控制提供理论基础。

（3）仿真结果表明时滞τ=20ms 时相对于被动悬置，以及在最优控制下的发动机悬置，设计的TLQG 控制器对发动机质心加速度，悬置动行程及车身质心加速度这几个性能指标都有一定的改善，从而一定程度上改善发动机的隔振性能。