双渠道零售商和传统零售商的定价策略

孙红霞, 李晓芳, 周 珍

(1.北京工商大学电商与物流学院, 北京 100048；2.首都师范大学管理学院, 北京 100089)

1 引言

随着世界经济一体化和信息技术的快速发展，现代商业市场的竞争更加激烈。物流产业和电子商务的相继发展，使制造商不再固守传统零售渠道，纷纷开通了电子直销渠道。根据《纽约时报》的统计，超过42%的美国制造企业纷纷开通了自己的网络零售渠道，如IBM、戴尔、耐克等。在制造商积极设立网络零售店的同时，B2C综合购物平台也伴随着互联网的发展活跃起来。互联网涌现了一批像亚马逊、京东这样的网络零售渠道，电子商务的发展势不可挡，传统零售商在电子商务浪潮中面临巨大挑战。他们一方面要接受制造商开辟网络渠道的事实，另一方面还要应对其他开辟网络渠道零售商的挑战，销量和利润都受到了极大的影响。

为适应市场环境的变化，一些传统的零售企业开始开辟网络销售渠道，如国美和苏宁等建立了自己的网络旗舰店。从零售商的角度看，开辟网络渠道的零售商会激励传统零售商提高经营质量，并且传统的零售商与开辟网络渠道的零售商之间存在着价格竞争和销量竞争。从顾客角度看，零售商开辟网络渠道后，顾客选择的多样性增加了。一部分顾客会选择网络渠道是因为网络渠道有着更短的订货周期，更小的运输路程，提供的产品价格一般也比较低廉，还为顾客节省了购物时间和交通成本，十分具有竞争力。由于传统渠道是更为普遍和成熟的营销模式，有着更高的顾客体验满意度，所以传统零售商有其自身的优势。但是当零售商开辟网络渠道后，销其售系统变得更为复杂，在此背景下，开辟网络渠道的零售商和传统零售商之间该如何确定各自的最优定价，如何制定价格竞争策略称为双渠道零售商和传统零售商要考虑的关键问题。因此，有必要对双渠道零售商和传统零售商间的竞争行为进行研究，分析他们的最优定价策略。

目前，在供应链混合渠道方面，渠道的选择策略和渠道的定价策略等问题引起了国内外学者的关注。渠道的选择策略方面，Dumrongsiri等[1]研究了包含一个供应商和一个零售商的双渠道供应链，研究结果表明当供应链进行集中决策的时候，制造商通过开辟网路渠道可以提高整体供应链的利润。Cai Guangshu[2]研究了双渠道供应链的渠道选择和协调问题，研究结果表明供应商和零售商的对于渠道的选择和偏好取决于渠道的运营成本、渠道的可替代性和整条供应链的利润。Khouja等[3]研究了制造商渠道选择和价格设定问题，研究结果表明渠道选择的最关键因素是每单位产品的可变成本。曹宗宏等[4]在单渠道零售商销售品的供应链中，建立了制造商开通直销渠道与零售渠道竞争，零售商提供自有产品与品牌产品竞争的供应链竞争模型，研究了开通直销渠道和提供自有产品的条件、双方的定价策略。Xiao Tiaojun等[5]在双渠道供应链中研究了渠道结构问题，指出由于直接渠道的定制产品，开辟直接渠道增加了单位产品的零售价格和销售价格。Zhang Weiguo等[6]对于制造商拥有传统渠道、直接网络渠道和在线购物平台的三渠道供应链，通过三个案例研究了需求分布、利润行为、最优定价策略和渠道选择策略。Li Bo等[7]研究了双渠道供应链成员的定价及绿色度问题，指出当绿化成本大于给定的阈值时，制造商不会开辟直销渠道。孔造杰和李祖一[8]在制造商实施直销渠道的背景下，研究了零售商开辟电子渠道对供应链的影响。目前已有文章对于供应商和零售商的渠道选择问题，主要集中于制造商开辟双渠道情境下，渠道选择的影响因素或者定价及协调问题，而没有考虑下游供应链中零售商的竞争行为。然而，在现实生活中，为了扩大商品的市场占有率，供应链中的一些零售商同时拥有网络销售和实体店销售模式，且单渠道和双渠道零售商间也存在多种复杂的竞争行为，因此有必要在供应链成员的定价问题中考虑零售商的竞争行为。

渠道的定价策略方面，Zhao Jing等[9]研究了两个制造商的不同的竞争策略和渠道成员的不同权力结构对最优定价决策的影响，构建了一种集中模式定价模型和七种分散模式定价模型，并利用博弈论方法得到了相应的分析均衡解。Yang Shanlin和Zhou Yongwu[10]对于包含一个制造商和两个零售商组成的单渠道供应链，在两个竞争零售商在三种不同的竞争行为下分析了制造商和零售商的定价策略。Chen Yunchu等[11]在供应商开辟网络渠道情形下，研究了供应链的定价策略，利用Nash和Stackelberg博弈给出了产品的定价方案。Hsieh等[12]在不确定需求下考虑了由多个制造商和一个零售商的供应链，在分散和集中决策情形下研究了了供应链成员的价格均衡决策。Huang Hu等[13]考虑了包括一个制造商和两个双寡头零售商供应链中的定价竞争问题，通过构建六种分散博弈模型来研究定价策略对供应链成员绩效的影响。赵连霞[14]通过建立制造商开通网上销售渠道以及零售商同时拥有网上销售渠道和传统销售渠道的混合定价决策模型，研究了制造商开通网上直销渠道并给制造商提供折扣契约的均衡决策问题。张喜征等[15]针对传统零售市场中存在同类已有产品竞争的情况，对Salop环形城市模型进行拓展，研究了电子商务环境下可替代产品的双渠道供应链定价策略。Modak等[16]在Stackelberg博弈下，分析了循环利用和产品质量水平对两级闭环供应链定价决策的影响。Ding Qing等[17]考虑了一个制造商和一个零售商的双渠道问题，通过分层定价决策过程，给出批发价格，传统渠道的零售价格和直接渠道的销售价格的联合最优策略。张学龙等[18]针对事前不确定性导致的退货问题,从消费者行为出发,通过Stackelberg博弈模型研究了四种不同市场需求情形在不同定价模式下双渠道供应链的最优决策。李建斌等[19]考虑由制造商、网络零售商和实体零售商组成的双渠道供应链，在零售商之间存在价格竞争和双向搭便车的情形下，研究集成和分散供应链两种模式下最优定价和努力水平决策。对于双渠道供应链的定价问题，目前的文章主要集中在制造商开辟网络渠道的定价问题，或传统竞争零售商的最优定价问题。随着互联网和电子商务的发展，很多零售商开辟了自己的网络渠道，这必然对没有开辟网络渠道的零售商产生冲击，因此有必要在零售商开辟双渠道情形下，根据零售商的竞争行为，分析双渠道零售商和传统零售商的定价策略问题。

本文将在上述研究的基础上，考虑由一个制造商和两个具有竞争行为的零售商组成的供应链，其中一个零售商采取传统销售和网络销售相结合的混合渠道，另外一个零售商仅有传统销售渠道，在两种不同模式下分析了两个零售商间的最优定价策略，并讨论了相关参数对各渠道最优定价的影响，最后用数值算例分析了模型的相关参数对最优利润的影响。

2 问题描述和模型假设

考虑由一个供应商和两个竞争零售商组成的供应链，其中零售商R1只有一条销售渠道，零售商R2同时进行实体店和网络销售渠道。如图2.1所示

图2.1 零售商增加直销渠道后的竞争模型

假设供应商生产同质产品，其目标是确定批发价格使利润最大化。供应商和零售商之间进行Stackelberg博弈，其中供应商是博弈的领导者，零售商是博弈的跟随者，两个零售商之间也进行Stackelberg博弈，根据博弈的先后顺序，两个零售商竞争时共产生两种模式：

模式1：零售商R1为领导者，零售商R2为追随者；

模式2：零售商R2为领导者，零售商R1为追随者。

假设市场的需求函数设定如下:

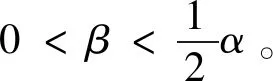
零售商R1和零售商R2的利润分别如下:

∏r1=(p1r-w)(d1r-αp1r+βp2d+βp2r)

(1)

∏r2=(p2d-w)(d2d-αp2d+βp1r+βp2r)

+(p2r-w)(d2r-αp2r+βp1r+βp2d)

(2)

供应商的利润如下:

∏s=(w-c)(q1r+q2d+q2r)

(3)

其中w为供应商的批发价格，c为成本。

3 零售商间竞争博弈分析

3.1 模式1:零售商R1为领导者，零售商R2为追随者

在该情形下，零售商R1首先确定销售价格来最大化自己的利润，零售商R2在获知零售商R1的销售价格后，通过调整自己产品的销售价格，以此最大化自己的利润。即零售商R1确定p1r，零售商R2确定其不同销售渠道单位产品的售价p2d和p2r，使自己销售利润最大。

零售商R2的利润函数∏r2关于p2d和p2r的一阶最优化条件分别为:

(4)

(5)

进一步可得∏r2关于p2d和p2r的Hessian矩阵为：

(6)

(7)

其中*表示最优结果，上标i(i=1,2)表示第i种模式。

将式(6)和(7)代入式(1)，零售商R1利润函数∏r1关于p1r的一阶和二阶最优化条件分别为：

(8)

其中A=α2-β2-αβ。

联立式(6)、(7)和(8)，代入式(3)，供应商的利润函数的二阶最优条件为:

(9)

(10)

其中B=3α3-4α2β-2αβ2+2β3。

结合式(10)与(1)-(3)和(6)-(8)可以得到模式1情况下，零售商R1和的最优零售价、最优利润及供应商的最优批发价和最优利润。

3.2 模式2:零售商R2为领导者，零售商R1为追随者

零售商R2先确定销售价格来最大化自己的利润，零售商R1在获得零售商R2的销售价格后，通过调整自己产品的销售价格，以此最大化自己的利润。即零售商R2确定其不同销售渠道单位产品的售价其不同销售渠道单位产品的售价p2d和p2r，零售商R1确定p1r，使自己销售利润最大。

零售商R1利润函数∏r1关于p1r一阶和二阶最优条件分别为:

(11)

将式(12)代入式(2)，则零售商R2的利润函数∏r2关于p2d和p2r的一阶最优条件分别为:

进一步可得∏r2关于p2d和p2r的Hesse矩阵为:

(12)

(13)

其中D=(β2+αβ)d1r+(α+β)(2α2-αβ-2β2)w。

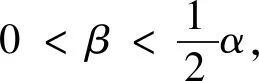
(14)

结合式(14)与(1)-(3)和(11)-(13)可以得到在模式2情况下，零售商的最优零售价、最优利润及供应商的最优批发价和最大利润。

3.3 结果分析

通过对前面的结果进行分析，可得如下命题。

命题1 当d2d=d2r时，无论在哪种模式下，零售商R2在两种渠道下具有相同的最优定价。

证明 在模式1下，将式(8)代入式(6)和(7)可得:

假设d2d=d2r=d时，有:

同理，在模式2下，当d2d=d2r=d时，根据式(12)和(13)，可得:

命题1表明，对于开辟网络渠道的零售商R2来说，当其线上和线下需求量一样时，在Stackelberg博弈下，不管是做主导者还是跟随者，其最优定价策略为线上线下价格一样。

证明 假设d1r=d2d=d2r=d时，在模式1下，

因此

命题2表明，当零售商R1面临的线下需求与零售商R2面临的线上及线下需求无差异时，零售商R1作为领导者时最优定价策略的线下价格小于作为跟随者时的线下价格。并且供应商的最优定价决策一样。

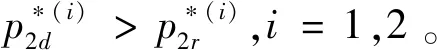
证明 当d2d>d2r时，在模式i下

命题3表明当网络渠道潜在市场份额大于传统零售渠道潜在市场份额时，双渠道零售商的网络渠道的最优定价大于传统零售渠道的最优定价。

4 数值分析

考虑到模型的复杂性，本节将用数值算例分析市场需求参数d1r、d2d,d2r及参数α和β对最优价格和最优利润的影响。首先，选取了5个算例分析市场需求参数对最优结果的影响，如表1所示。

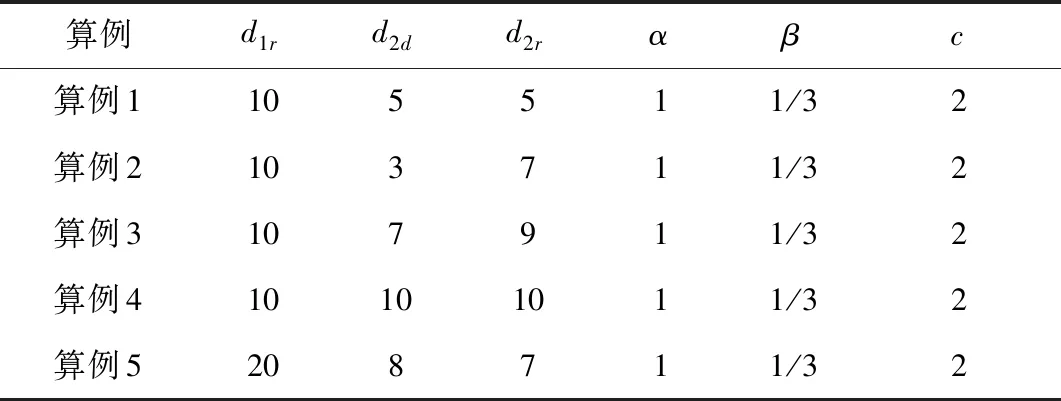
表1 数值算例选取

算例1描述零售商R1与零售商R2的市场总需求相同，且及零售商R2的线上和线下的需求也相同的情况，即市场需求关系为d1r=d2d+d2r且，d2d=d2r。算例2描述在算例1的基础上，改变了零售商R2的线上和线下的需求。算例3描述零售商R1的市场需求小于与零售商R2的情况，即市场需求的关系为d1rd2d+d2r。

根据设定的算例，零售商和供应商的最优定价和最优利润如表2所示。

表2 给定算例的最优价格和最优利润

由表2可以得到如下结论：

(1)当两个零售商的市场需求相同时，对于供应商来说，在同一种模式下，其最优批发定价以及最优利润相同。对于零售商来说，其最优定价随着需求的增加而增大。

(4)市场需求越大，即d1r,d2d,d2r越大，其零售商R2和和供应商的最优利润越大，这说明面临市场需求越大，其零售商和供应商的利润越大。

在现实情况中，零售商R1和零售商R2面对同一市场，彼此之间的市场需求相差不大。为了使后文更容易分析，这里我们假设了一种理想情况：当零售商R1和零售商R2面临相同的市场需求，即d1r=d2d+d2r时，采用算例2设定的参数，进一步分析了α和β同时变化时，对零售商和供应商最优利润的影响，结果如图1-图4所示。

图4 α,β变化时对两种情形下零售商利润差的影响

图3 两情形下α,β对供应商利润差的影响

图2 情形2下α,β对零售商利润差的影响

图1 情形1下α,β对零售商利润差的影响

5 结语

在激烈的市场竞争环境下，为了在市场中取得竞争优势，零售商已意识到开辟网络渠道的重要性。越来越多的零售商开辟的网络销售渠道，在此背景下，本文考虑了考虑单制造商和双零售商组成的二级供应链，在该模型中，假定两个零售商销售同质产品进行价格竞争，供应商和零售商及两个零售商间均进行Stackelberg博弈，分别针对双渠道零售商和传统零售商作为领导者的情况，建立了开辟了网上双渠道零售商和传统零售商的定价决策模型。研究结果表明：当交叉价格弹性系数相等且顾客选择购买渠道受交叉价格弹性系数的影响为低灵敏性的条件下，零售商倾向于作为Stackelberg的领导者，而供应商更倾向于传统渠道的零售商做领导者。从利润的角度看，对于供应商而言，传统渠道的零售商做主导者时的总利润要比双渠道零售商做主导者时的总利润大，对于零售商来说，作为领导者时的总利润要比作为追随者时的总利润大。

本论文的研究为供应链成员的竞争策略提供了理论依据，有助于决策者对于如何选择销售渠道及设定销售价格做出更加科学合理的决策。本文的研究结论是在一定的前提假设下得到的，由于市场环境的复杂性，今后的研究可以从以下方面进行：一方面，消费者的需求对渠道的选择有一定的影响，因此可以基于消费者的偏好，考虑双渠道零售商和传统零售商的竞争的情形。另一方面，由于市场需求的不确定，可以不确定环境下考虑零售商间的竞争问题。