EPS颗粒混合轻量土动力变形特性离散元分析

兰 鑫，侯天顺，杨 艳，张亚飞

(西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100)

EPS(Expanded Polystyrene，EPS)颗粒混合轻量土作为轻质土的一种，是由发泡聚苯乙烯(EPS)颗粒、原料土、水泥和水按照一定比例均匀混合搅拌压实而成的新型轻质土工材料[1,2]。由于轻量土具有轻质高强、缓冲性、施工工艺简单、强度和密度可调节、废物再生利用等优良特性，其作为工程填料，广泛应用于铁路、公路、码头、桥头等方面[3～5]。这些基础设施在建设使用过程中，交通荷载、地震荷载等作用对构筑物造成了较大的破坏，严重影响了基础设施的安全性、适用性和耐久性，因此不可忽视动力荷载因素对材料的作用，对EPS颗粒混合轻量土动力特性的研究存在必要性[6～8]。

目前对于EPS颗粒混合轻量土动力特性方面的研究主要依靠室内动三轴试验。高玉峰等[9～11]通过室内动三轴试验研究了轻质土在动荷载作用下的变形特性，发现轻质土的动应力-应变骨干曲线具有双曲线形态。当动应变相同时，随着固结围压、振动频率、水泥掺量和试样养护龄期的增大，轻质土的阻尼比减小而动应力增大，在相同的动应力作用下，动应变随着固结围压、振动频率、水泥掺量和试样养护龄期的增大而减小。王庶懋等[12～14]基于砂土与EPS颗粒混合的轻质土动三轴试验结果，建立了与水泥掺量、围压等因素相关的割线剪切模量Gsec的经验衰减模型。他发现割线剪切模量与动应变呈双曲线关系，与围压为指数关系，由于水泥胶结的约束作用，割线剪切模量对围压的依存度随水泥掺量的增加而减小。Gao等[15,16]利用EPS颗粒混合轻质土空心圆柱试件进行复合轴扭转试验，研究了复合应力路径下的动力特性，发现EPS颗粒混合土受混合比和初始应力状态的影响具有动态非线性特性。EPS颗粒含量对EPS颗粒混合土的初始剪切模量和线弹性阶段的循环应力-应变曲线影响不大，增大水泥掺量可以有效地提高EPS颗粒混合土的动强度。

在基于离散元软件进行三轴试验细观层次研究方面，李识博等[17,18]利用PFC3D软件建立黄土三轴试验模型，探讨黄土三轴剪切过程中的细观变化，发现数值模型中细观参数与宏观弹性模量、泊松比及破坏强度有密切的联系，如试样弹性模量取决于法向刚度kn，泊松比取决于刚度比kn/ks(ks为切向刚度)，破坏强度取决于摩擦系数，且位移场和接触应力场的变化规律与室内三轴试验宏观现象较一致。蒋应军等[19]基于PFC2D软件构建了级配碎石动三轴试验数值模型，通过数值模拟分析了试验条件及其细观力学参数对骨干关系的影响规律，提出了离散元模拟的试验条件和微力学参数标定方法。金磊等[20～22]进行了不同含石量的土石混合体大三轴试验数值模拟研究，发现随着含石量的增加，试样破坏强度、残余强度、弹性模量和破坏应变逐渐增大，剪缩性减小，剪胀性增强。Michael等[23,24]在考虑颗粒尺寸分布和初始相对密度的条件下，建立土工格栅数值模型，并结合室内三轴试验，研究了粒状材料的双轴土工格栅试件的应力-应变特性。根据土体和土工格栅的相互作用，该模型可用于分析土工格栅试件稳定性连锁效应。

通过诸多学者对EPS颗粒混合轻量土动力特性的研究，发现EPS颗粒混合轻量土的应力传递、裂隙发展、剪切破坏和承载能力等方面与一般的均质土体存在一定差异，而产生这种差别很大程度上依赖于轻量土内部结构特征，如颗粒分布排列、运动位移、接触摩擦等。利用PFC3D离散元软件数值模拟，从细观层面上探究EPS颗粒与土颗粒间的相互作用机制，与宏观力学响应相结合，能够更深入地揭示轻量土特殊的力学特性与变形破坏特征。因此探究其动力变形细观机理尤为重要，但目前国内外罕见对EPS颗粒混合轻量土细观层面的研究。

基于此，本文开展EPS颗粒混合轻量土室内动三轴试验，并利用PFC3D离散元软件建立相应数值模型。通过对比数值模拟和室内试验的滞回曲线，论证数值建模的可行性。通过分析EPS颗粒混合轻量土摩擦系数、刚度比和黏结强度等细观参数对骨干曲线的影响规律，以及试样的接触力分布图、位移场，将细观机理与宏观特性相结合，阐明EPS颗粒混合轻量土动力变形特性的本质，为轻量土的工程应用提供理论参考。

1 轻量土室内动三轴试验

1.1 试验材料

试验的黄土取自陕西杨凌地区，呈黄褐色，属于低液限粉质黏土。根据轻型击实试验，试验用土的最优含水率wop=20.51%，最大干密度ρd=1.69 g/cm3，基本物理性质指标如表1所示。本次试验采用轻质材料为EPS颗粒，粒径3～5 mm，堆积体密度为0.0087 g/cm3，纯颗粒密度为0.0138 g/cm3。固化剂采用复合硅酸盐水泥，强度等级32.5，纯颗粒密度为3.12 g/cm3。水为普通自来水。

表1 杨凌黄土的基本物理性质指标

1.2 试样制备

在制备试样时，按计算比例将原料土与水泥混合，加水搅拌至泥浆状，称取EPS颗粒掺入并充分搅拌使其混合均匀。然后填入直径39.1 mm，高80.0 mm，内壁套有一层保鲜袋的三瓣模中，并尽可能捣实，保证试样密实度一致。在标准养护箱(温度20±2 ℃，湿度>95%)中养护24 h后脱模，并继续养护至28 d龄期。将试样抽真空1 h，并浸水24 h，使试样饱和后进行动三轴试验。

1.3 试验方案

试验采用STD-20型土动三轴试验机，试样高为80.0 mm，直径为39.1 mm，EPS颗粒掺量为1.26%(体积比为50%)，水泥掺量为15%，含水率为50%(均以干土的质量为基准)。分别按照50，100，150，200 kPa的固结应力施加围压，对试样进行排水固结，固结应力比Kc=1.0。固结结束后，进行不排水动三轴试验，施加正弦波循环荷载，动剪应力比取0.075，振动频率为1 Hz，逐级加荷，每级振动10次，采用应力控制式，以轴向应变达到5%为破坏标准。

1.4 试验结果

滞回曲线表达了试样在动力荷载作用下的动应力-应变关系，实时地反映了试样在振动过程中的变化情况，体现出试样的动力特性。由于在轻量土中掺加了15%的水泥固化剂，试样整体刚度较大，抵抗变形能力强。在动力试验过程中，当施加压应力时，轻量土试样表现出一定的强度，当由压应力转变为拉应力时，试样不会被拉伸，导致与振动轴分离不接触，因此所得滞回曲线仅有压应力部分。由图1可知：(1)滞回曲线反映了动应变对动应力的滞后性，随着动应力幅值的增大，滞回圈更加“饱满”，宽度和面积加大，说明动应变滞后于动应力的相位增大；(2)随着逐级加荷的增大，滞回圈动应力峰值与所对应的轴向应变不断增大，直至试样破坏，说明轻量土具有应变硬化特性；(3)在作用较大的动荷载时，轻量土中塑性变形的出现使滞回曲线的动应力发展变缓，滞回曲线的中心点逐渐向应变增大方面移动，说明轻量土具有应变累积性。

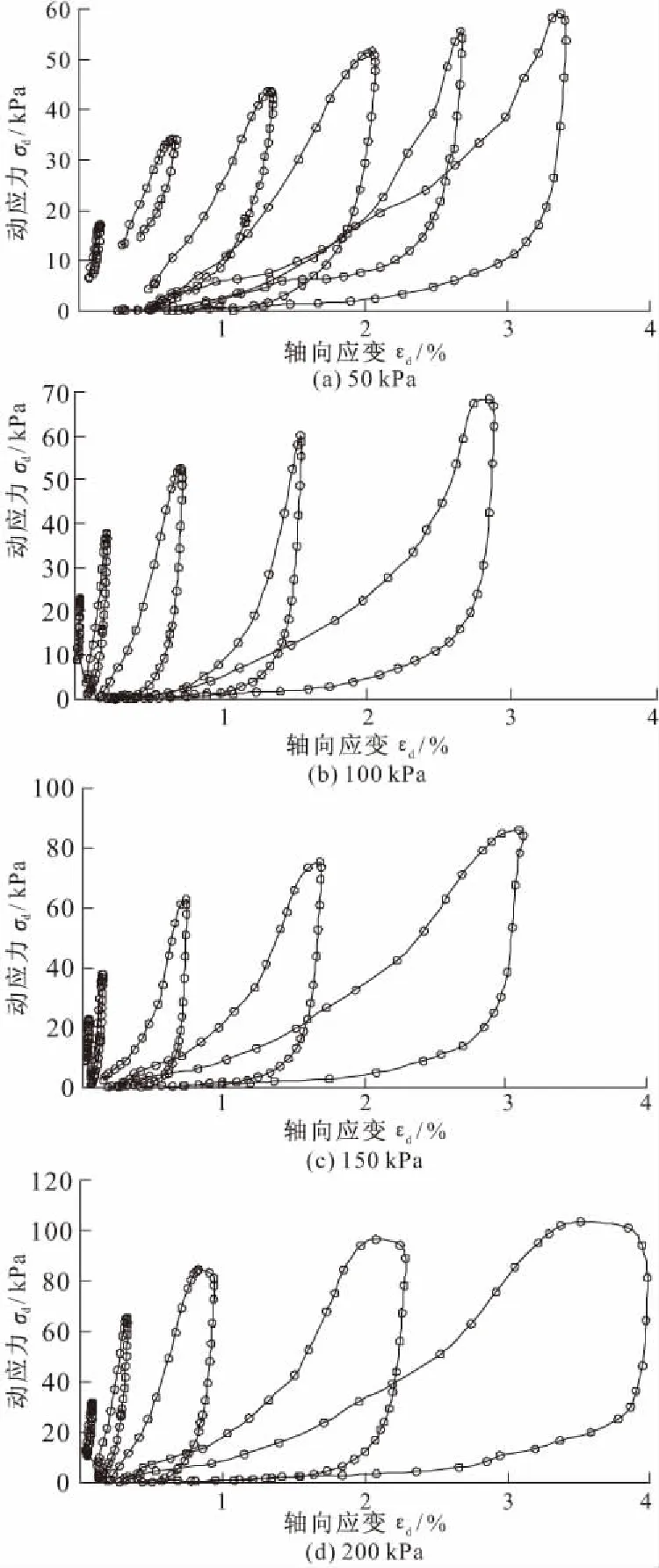
图1 不同围压下EPS颗粒混合轻量土室内动三轴试验滞回曲线

2 轻量土动三轴试验数值建模

2.1 力学原理

与连续介质力学方法不同，PFC(Particle Flow Code)介质的基本构成为颗粒，从细观结构角度研究介质的力学特性和行为。PFC中的颗粒为刚性体，但在接触部位允许重叠，以模拟颗粒之间的接触力。在计算过程中，允许颗粒发生有限的位移、旋转，系统内部可以自动辨识新的接触，结合牛顿第二定律，将颗粒间的力学关系处理成颗粒的运动方程和接触的力-位移方程。当颗粒间的接触关系发生变化时，通过接触力传递影响颗粒的运动，颗粒更新位置产生新的接触，周而复始，介质的宏观力学特性受到影响，因此介质内颗粒接触状态的变化决定了介质的本构关系，如图2所示。

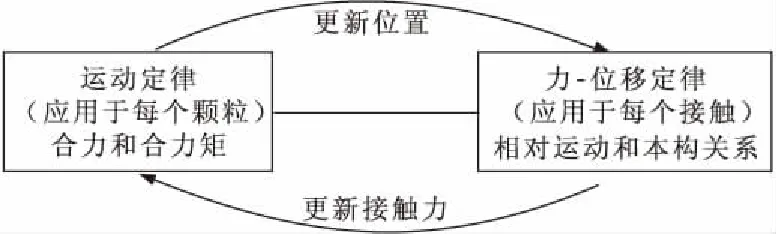
图2 离散元方法计算循环图示

2.2 建立模型

建立圆柱形(Cylinder)墙体和上下两个加载板，模拟动三轴试验三轴室，以约束散体材料，初始尺寸高为80.0 mm，直径为39.1 mm，如图3a所示。然后建立不同级配的土颗粒和EPS颗粒组(Group)，使其均匀分布，构成EPS颗粒混合轻量土骨架体系，如图3b所示，其中黄色颗粒表示土颗粒，灰色颗粒表示EPS颗粒。颗粒材料为刚性材料，颗粒之间采用接触黏结模型，以模拟黄土的黏聚力和水泥的固化胶结作用。

在整个计算过程中，用球形颗粒的位移运动来模拟室内动三轴剪切过程中土和EPS颗粒的运动变化情况。通过伺服机制对试样施加围压，待边界条件达到指定围压，则对上下加载板不再伺服控制。加载过程中，控制上下加载板的运动速度为正弦波形式，实现循环加载，试样的动应力为颗粒与加载板接触所作用的力除以板的面积，轴向应变为加载板的相对位移除以试样的初始高度。

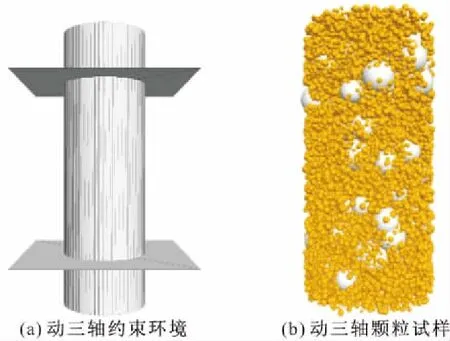
图3 轻量土动三轴数值模型

3 细观参数分析

EPS颗粒混合轻量土是一种结构性土，其抗剪强度主要取决于颗粒间的黏结力、摩擦力和咬合力。在模拟过程中，采用控制变量法，通过定义不同颗粒组摩擦系数、刚度比、黏结强度等细观参数，赋予模型材料属性，以细观参数反映材料的宏观力学特性，探究不同细观参数的变化对破坏强度的影响规律，分析其对宏观力学特性的作用机理。

3.1 摩擦系数

摩擦系数μ反应了颗粒运动的阻尼，是模型内部颗粒间的摩擦效应。颗粒法向刚度取3.0×108N/m，切向刚度取1.0×108N/m，法向和切向接触粘结强度均取3.0×108N/m，通过分别改变EPS颗粒和土颗粒的摩擦系数，得到100 kPa围压下轻量土模型的骨干曲线，探究两者之间的内在联系。

从图4可以看出，不同摩擦系数下的骨干曲线变化趋势相近，随着摩擦系数的增大，骨干曲线的破坏强度不断增长。在整个试样模型中，共有土-土颗粒、土-EPS颗粒、EPS-EPS颗粒、土颗粒-墙体、EPS颗粒-墙体五种接触类型，由于土颗粒体积占比为50%且粒径小，所以大量分布于整个试样模型内。土颗粒的摩擦系数由0.1增加到0.2，0.4，0.8时，相应会增大模型内部土-土颗粒、土-EPS颗粒、土颗粒-墙体三种接触的摩擦系数，这三种接触遍布试样内部，使颗粒运动阻尼效应增大，整体提升试样的抗剪强度。以土颗粒摩擦系数为0.1所对应的破坏强度为标准，破坏强度分别提高了16.71，23.12，42.97 kPa，相对强度增长率为31.46%，43.53%，80.91%。

图4 不同摩擦系数下的动三轴数值模拟骨干曲线

同理增大EPS颗粒的摩擦系数时，模型内EPS-EPS颗粒、EPS-土颗粒、EPS颗粒-墙体三种接触的摩擦系数也随之增大，使试样破坏强度分别提升了14.86，21.48，31.90 kPa，相对强度增长率为27.98%，40.44%，60.06%。由于EPS颗粒粒径大、数量少，增大EPS颗粒的摩擦系数时，破坏强度的增长效果没有增大土颗粒摩擦系数时显著。

表2 不同摩擦系数下的破坏强度统计

3.2 刚度比

材料刚度比kn/ks反映了颗粒在法向和切向抵抗变形的能力。在摩擦系数取0.4，法向与切向接触粘结强度取3.0×108N/m，切向刚度不变的前提下，分别改变颗粒的刚度比，得到100 kPa围压下轻量土模型的骨干曲线(图5)，探究二者对试样的影响规律。

从图5可知，随着颗粒刚度比的增加，数值试样的破坏强度均出现逐渐增长的变化趋势，破坏强度所对应的轴向应变不断减小。在土颗粒切向刚度不变的前提下，土颗粒刚度比从1.0分别增加到2.0，3.0，4.0，所对应的数值试样破坏强度从68.03 kPa增加到68.17，74.06，76.69 kPa，分别增加了0.21%，8.86%，12.73%，小幅提高了试样初始弹性模量。这是由于土颗粒切向刚度不变，法向刚度增大，在颗粒接触挤压的过程中，颗粒切向抵抗变形的能力变强，提升了试样整体刚度，使试样整体抗剪强度有所提高，破坏强度对应的轴向应变减小，初始弹性模量略有增大。

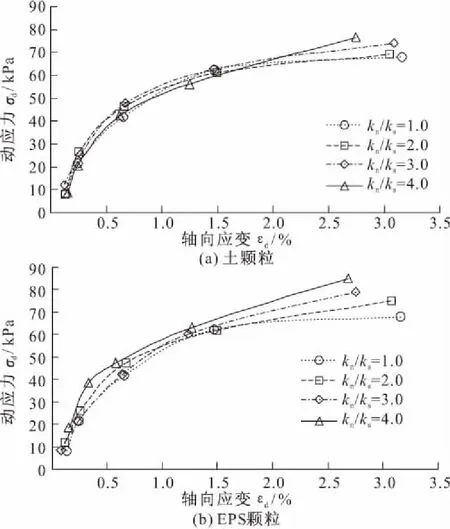
图5 不同刚度比下的动三轴数值模拟骨干曲线

同理，保持EPS颗粒切向刚度不变，增大法向刚度，破坏强度分别增大了10.13%，16.29%，24.97%，破坏强度对应轴向应变分别减小到3.08%，2.75%，2.68%。相较于土颗粒，EPS颗粒的刚度比对试样的破坏强度影响更大，二者对初始弹性模量影响相近。这是由于在试样中，EPS颗粒体积比土颗粒大很多，且体积占比达到50%，当改变EPS颗粒刚度比时，相比于土颗粒，对试样整体结构影响更大，使破坏强度增加更多，破坏强度对应轴向应变减小更显著。不同刚度比下的破坏强度统计结果如表3所示。

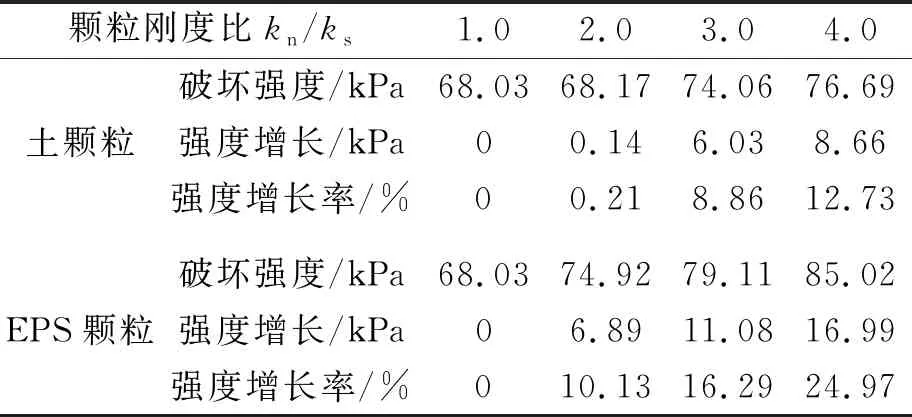
表3 不同刚度比下的破坏强度统计

3.3 接触粘结强度

在EPS颗粒混合轻量土试样中，原料土为黏性土，具有一定的粘聚力，且其中有15%含量的水泥，均匀散布在试样内，经过水泥的水解水化反应，在颗粒之间形成了较强的胶结作用，使试样具有了一定的“结构性”。在PFC3D数值模拟过程中，建立接触的法向粘结强度n_b和切向粘结强度s_b来反应试样内土体的粘聚力和水泥的胶结作用。颗粒摩擦系数取0.4，法向刚度取3.0×108N/m，切向刚度取1.0×108N/m，通过探究100 kPa围压下，不同接触粘结强度数值试样的骨干曲线，分析粘结强度对试样抗剪强度的贡献。

由图6可知，不同粘结强度下试样的骨干曲线变化趋势基本一致，呈应变硬化型，随粘结强度的增大，试样破坏强度显著增大。当粘结强度增大时，相应的破坏强度分别增加了8.09，31.11，39.13 kPa，增长率为11.97%，46.03%，57.90%，可见粘结强度对试样的抗剪强度有较大影响。在模拟过程中，增大颗粒间的粘结强度，对应于室内试验中改变试样的配比，增大水泥的掺入比，增强水泥胶结作用，使试样内粘结效果更显著，增大试样的抗剪强度，这与黎冰等[25]的试验结果相同。

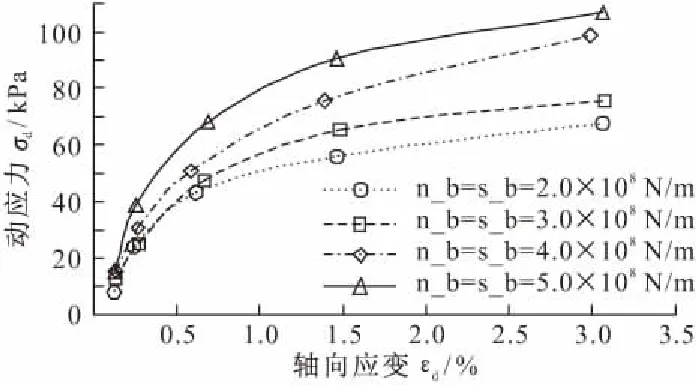
图6 不同粘结强度下的动三轴数值模拟骨干曲线

当围压增大时，颗粒之间相互挤压接触更紧密，接触力更大，相同摩擦系数下，根据滑动摩擦公式：f=μF(式中：f为颗粒间摩擦力；F为颗粒间接触力)，颗粒间摩擦强度不断增大。而粘结强度不会随围压的增大而变化，当颗粒间应力大于粘结强度时，粘结会断裂。因此在高围压下，粘结强度对试样抗剪强度的贡献基本不变，而摩擦强度的贡献相对于粘结强度的贡献增大，使试样更具延展性。

4 宏观响应与细观机理分析

为了使数值模拟得到的滞回曲线与室内动三轴试验结果吻合，根据不同细观参数的敏感性分析，不断调整PFC3D数值模型细观参数。将侧墙刚度设置为上下加载板的1/10，以模拟橡皮膜柔性边界，最终选取的细观参数如表4所示。

表4 数值模型细观参数

4.1 数值模拟结果与室内试验结果的对比

对比不同围压下轻量土室内动三轴试验滞回曲线和数值模拟结果，如图7所示，其中EPS颗粒体积比为50%，水泥质量比为15%。将100 kPa围压下数值模拟每级滞回曲线的第六周顶点标记为A～E点。由图7可知：(1)不同围压下，室内动三轴试验滞回曲线与模拟结果基本吻合，随着振动级数和围压的增大，二者的动应力峰值逐渐增大。每个振动周期内，室内试验和数值模拟的动应力峰值及所对应的动应变相近，说明三维离散元模型可以较好地模拟轻量土室内动三轴剪切试验。(2)数值模拟和室内试验的滞回曲线仍存在一定的差异，分析其原因主要为：在数值模拟过程中，颗粒均为刚性球体，其形态特征和受力状态与实际土样存在偏差，且EPS颗粒相对于土颗粒较大，颗粒之间易发生错动滑移，使受力产生变化，应力分布不均匀。当压应力转变为拉应力时，室内试样具有弹性变形，橡皮膜具有一定的抗拉强度，试样与振动轴缓慢脱离，动应力逐渐降低。而数值试验中，对墙体施加反向速度以模拟应力方向的转变，使试样与墙体产生了快速分离，所以此时动应力迅速降低。

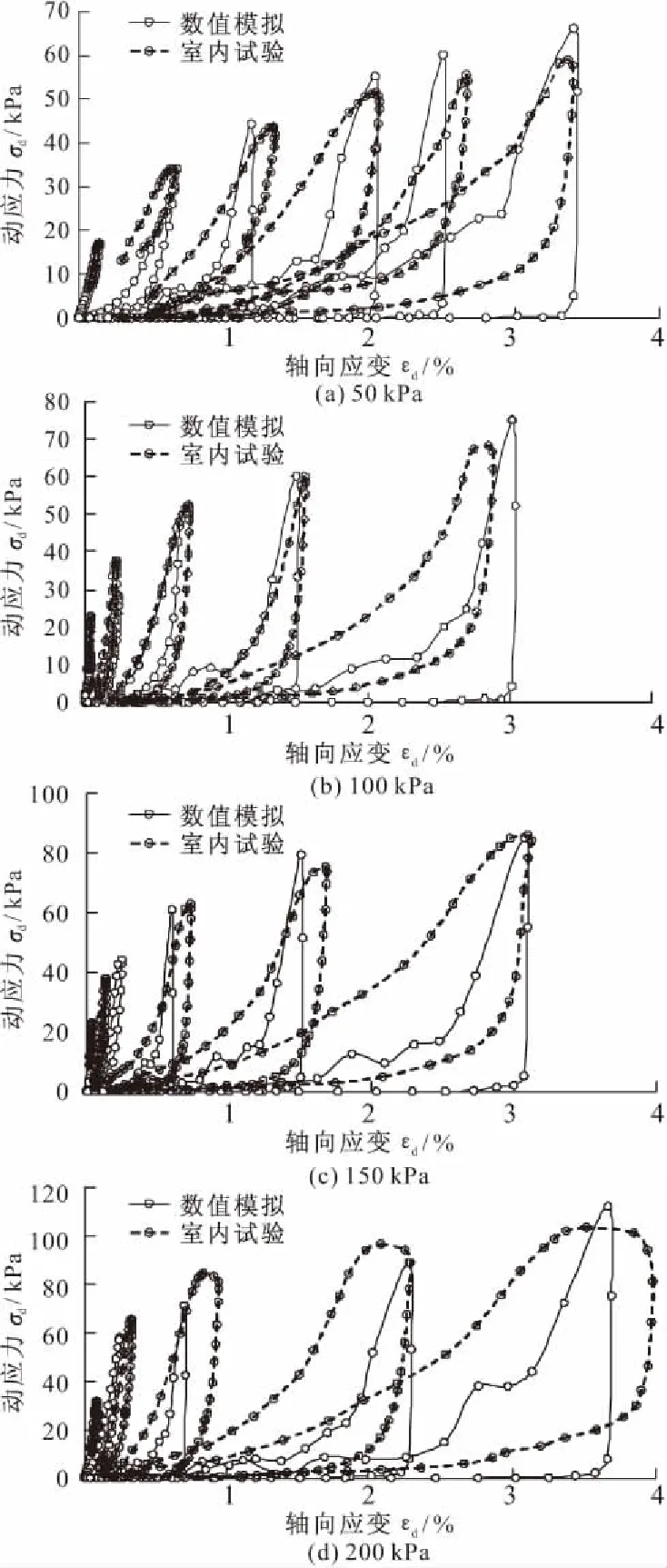
图7 不同围压下轻量土动三轴试验滞回曲线与数值模拟结果的对比

4.2 接触力

试样内部颗粒间的接触力反映了EPS颗粒混合轻量土动三轴剪切过程中的受力状态，可以从细观探究颗粒间的应力传递。在轻量土动三轴数值模拟过程中，采用分级加载，在100 kPa围压下，当每级动应力达到峰值时，探究试样内部颗粒间应力传递。在接触力分布图(图8)中，使用切片工具切取5 mm剖层，力链的粗细与相接触颗粒的粒径成正比，为更好地呈现接触力和颗粒之间的关系，将颗粒缩小为原始大小的0.4倍。

从图8可知，随着荷载逐级递增，从A点到E点对应的时刻下，颗粒间接触力整体增大，且在各个阶段，按颗粒间接触力大小排列为：土颗粒-土颗粒>土颗粒-EPS颗粒>EPS颗粒-EPS颗粒。在围压和振动频率等条件不变的前提下，循环荷载加载前期，正弦波荷载振幅小，所产生的颗粒间接触力较小。随着逐级加载，正弦波荷载振幅递增，接触力逐渐增大，试样内整体受力增大，与滞回曲线中动应力峰值逐级递增的规律吻合。在PFC3D软件中，颗粒间接触力的大小与其材料的刚度呈正相关。EPS颗粒的法向和切向刚度均比土颗粒小，因此相较于EPS颗粒-EPS颗粒和EPS颗粒-土颗粒间的接触力，土颗粒-土颗粒间的接触力更大。所以试样在受力过程中，土颗粒构建了骨架体系，而EPS颗粒主要扮演减重角色，试样所受荷载大部分由土骨架承担，EPS颗粒受力较小。在加载过程中，循环荷载增大，试样内颗粒在力的作用下，竖直方向上向中部挤压，横向上向两侧挤压。这与室内试验结果相符，在动荷载作用下，试样累积了一定的塑形变形，竖直高度有一定减小，横向直径略有增大。

图8 每级加载过程中滞回圈顶点对应的接触力分布

4.3 位移场

在振动过程中，试样内部颗粒间作用力相互传递，颗粒在力的作用下不断发生位移，利用PFC3D软件将颗粒的运动位移情况呈现出来，通过分析100 kPa围压下轻量土数值模型位移场(图9)，探究每级加载过程中试样内部颗粒运动位移规律和数值试样动力变形机理。

由图9可知，轻量土数值模型在轴向荷载作用下，两端颗粒在竖直方向上向中部运动，中部颗粒在水平方向上向外围运动，较大的EPS颗粒对试样整体的位移规律基本无影响。试样加载过程中，两端颗粒的位移总是大于中部颗粒，随着荷载逐级增大，从A点到E点对应的时刻，颗粒位移整体增大。试样加载时，由上下加载板施加动力荷载，PFC计算中遵循牛顿第二定律F=ma(式中：m为颗粒质量；a为颗粒加速度)，试样上下两端颗粒在力的作用下发生位移运动并逐渐向中部传递，但试样内部的阻尼效应使向中部传递的位移逐渐减小，中部颗粒位移总是小于两端颗粒，表现出一定的“滞后性”。在PFC3D软件中，试样的宏观变形不是由于颗粒本身的变形，而是颗粒位置的变化引起的。在其它条件不变的情况下，随着逐级加载，试样两端受力增大，使颗粒位移整体增大，与滞回曲线中每级荷载作用下的轴向应变相对应，表现在宏观上为试样被压缩。

图9 每级加载过程中滞回圈顶点对应的位移场

5 结 论

通过进行不同围压条件下EPS颗粒混合轻量土室内动三轴试验和数值模拟，分析轻量土动力变形特性，主要得出以下结论：

(1)EPS颗粒混合轻量土室内动三轴试验的滞回曲线反映了轻量土动应变对动应力的滞后性，动应力峰值随围压的增大而逐渐增大，且轻量土具有应变硬化特性和应变累积性。

(2)随着颗粒摩擦系数的增大，轻量土数值模拟骨干曲线的破坏强度不断增长，相比于EPS颗粒，增大土颗粒的摩擦系数使破坏强度增长更加显著。随着颗粒刚度比增大，骨干曲线破坏强度增长，但破坏强度所对应的轴向应变减小，小幅提高了试样初始弹性模量。以黏结强度为2.0×108N/m对应的破坏强度67.58 kPa为标准，当黏结强度增大时，相应的骨干曲线破坏强度分别增长了11.97%,46.03%,57.90%。

(3)室内试验的滞回曲线中动应力下降缓慢，而数值模拟的滞回曲线波动较大且动应力下降迅速，但二者动应力峰值及所对应的动应变相近，说明三维离散元模型可以较好地模拟轻量土室内动三轴试验。在围压和振动频率等条件不变的前提下，随着逐级加载，颗粒间接触力整体增大，按颗粒间接触力大小排列为：土颗粒-土颗粒>土颗粒-EPS颗粒>EPS颗粒-EPS颗粒。数值试样内两端颗粒在竖直方向上向中部运动，中部颗粒在水平方向上向外围运动。中部颗粒的位移总是小于两端颗粒，表现出一定的“滞后性”，随着荷载逐级递增，颗粒位移整体增大，表现在宏观上为试样被压缩。