膨胀土膨胀时程特性试验及特征曲线参数确定

蒋 超，屈 祥

(1. 湖南建工交通建设有限公司，湖南 长沙 410004；2. 上海市政工程设计研究总院(集团)有限公司长沙分公司，湖南 长沙 410004)

膨胀土是一种高塑性黏土，富含蒙脱石、伊利石等膨胀矿物，其失水收缩，吸水膨胀的特性引起了许多工程问题[1,2]。为此，已有不少学者对膨胀土胀缩行为进行研究，而膨胀时程曲线则是研究膨胀土胀缩行为的重要课题之一。随着土力学理论和工程应用的发展，人们已经认识到膨胀土的最终膨胀变形主要由土体中的膨胀矿物决定。段尚磊研究发现膨胀土的膨胀力和变形能力与自身干密度和含水率有关[3]；杨和平等的试验表明膨胀土的最终膨胀率和膨胀压力受到力学边界条件的影响[4]。Siemens等人进行了不同种类膨胀土的膨胀试验，结果表明膨胀土的最终膨胀变形存在一个极限平衡，该平衡只与力学边界与土体自身属性有关，受应力路径影响较小，这一结论后续得到了Liu和Yuan等人的进一步证实[5～8]。此后，叶为民等将膨胀变形与时间建立关系，这就是膨胀时程曲线[9]。大量试验结果显示，膨胀土在一维浸水膨胀过程中，其膨胀时程曲线先迅速增长，随后增速减缓并最后趋于稳定[10～14]。这种膨胀时间曲线的特征可以用含参数α，β的负指数曲线表示，如式(1)所示[15]。

S(t)=α(1-e-βt)

(1)

式中：S为膨胀率；t为时间。

由于膨胀土胀缩特性非常复杂，受到多因素影响，目前常用的最小二乘法拟合常常不能很好地描述这种特性。因此，在进行曲线拟合和参数确定时会出现较大误差。文献[16]认为β是控制膨胀速率的因素，但不同种类膨胀土的膨胀试验证明(如川中红层泥岩、高庙子膨胀土、Maryland膨胀黏土、Callovo-Oxfordian膨胀黏土等)，膨胀土的膨胀速率并不为常速，尤其是在初始阶段膨胀速度非常快，并且上部荷载将对其膨胀速率产生非常大的影响，而通过最小二乘法拟合的β是一个常数，并不能承担描述膨胀速率的任务[17～20]。

为明确该模型参数的物理含义，给出更为合适的模型参数确定方法，本文首先通过试验测定有荷与无荷膨胀下的膨胀时程特征，此后引入物理学中的半衰期概念，利用数学方法对特征参数α，β进行新的解释，并给出了基于半衰期的参数确定方法。最后，将拟合结果与最小二乘法的拟合结果进行比较，证明半衰期参数确定方法的准确性和适用性。

1 膨胀特性试验方案

以张桑高速公路高路堑边坡膨胀土为试验土样，土样偏棕黄色，基本性质如表1所示，进行无荷膨胀率试验，得到该试样的自由膨胀率为73.6%，因此为中等膨胀性土。

表1 膨胀土试样基本物理指标 %

本试验的目的是获得膨胀土有荷膨胀和无荷膨胀的膨胀特征，并以此分析式(1)参数的物理含义。鉴于张桑高速位于湖南湘西地区，气候潮湿，常年多雨，其路基处于含水量增加的情况，因此进行不同上部荷载下膨胀土的一维膨胀试验以模拟张桑高速公路的实际工作状态。同时，进行无荷膨胀试验以掌握膨胀土的最大膨胀能力。

按照JTG E40-2007《公路土工试验规程》，配制目标含水率w为12%，15%，18%，21%的重塑膨胀土样。制备流程如下：(1)将取回的试样压碎成颗粒状，筛分后取2 mm以下颗粒，置于烘箱中烘干24 h；(2)取出干样，并加入蒸馏水直至试样达到目标含水率，搅拌均匀后放至环境湿度控制箱中静置48 h；(3)按照路基设计压实度，取不同质量的膨胀土并压至直径为61.8 mm的环刀内，随后将环刀放入固结仪内进行无荷膨胀和有荷膨胀试验。有荷膨胀的目标上部荷载为50，75，100 kPa。试验开始后，通过位移百分表读数并计算膨胀百分比。

2 试验结果及特征分析

2.1 试验结果

通过上述试验，得到了不同土体含水率下无荷与有荷膨胀的位移数据，计算膨胀百分比后将其与时间的关系曲线绘制于图1，2。

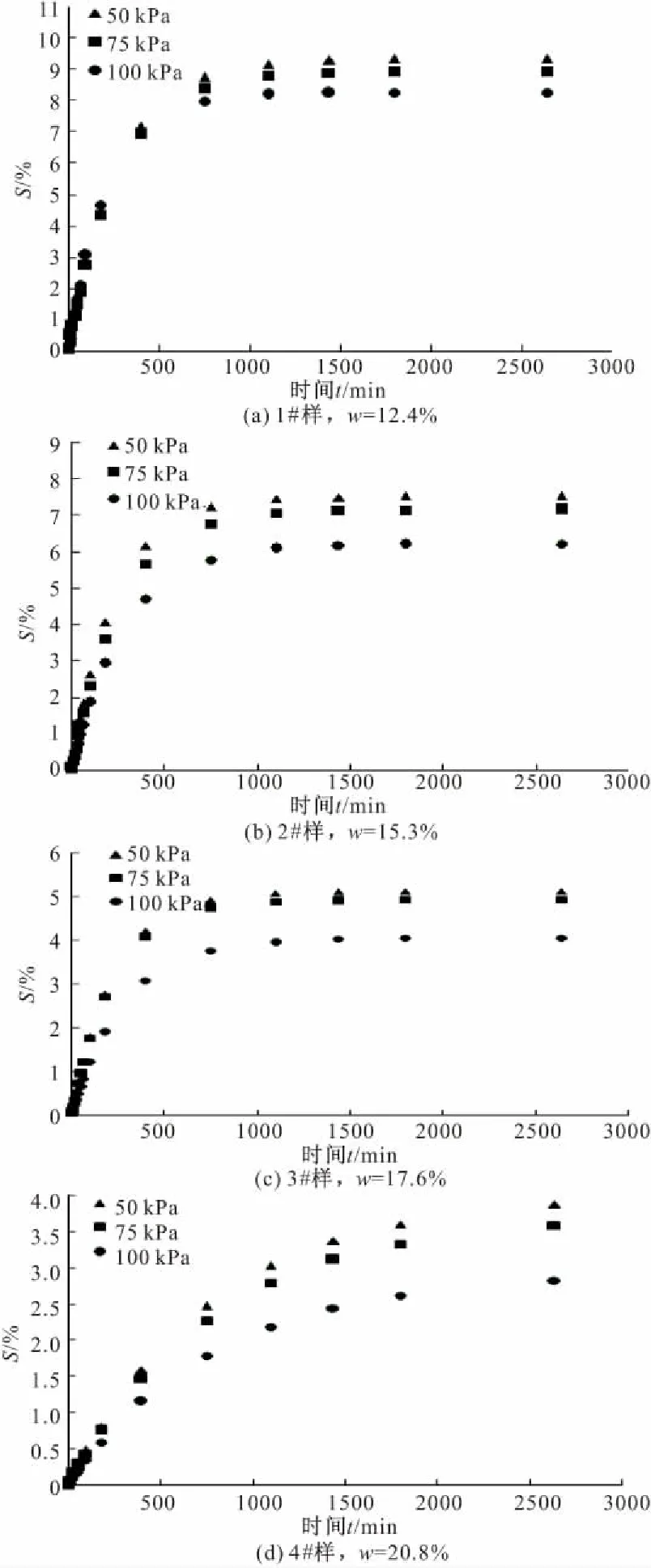
图1 同含水率下的有荷膨胀率与时间关系

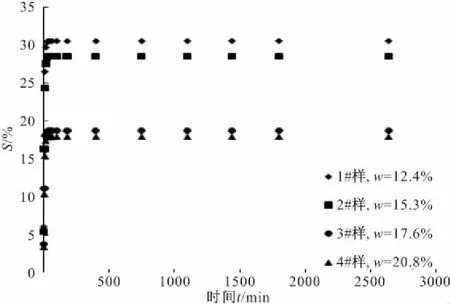
图2 不同含水率下无荷膨胀率与时间关系

从图1，2可以看出，有荷膨胀的膨胀时程曲线初始增长较快，而后续增速逐渐放缓并趋于稳定。对于50，75 kPa的情况，其最终膨胀率相差不大，但对于100 kPa的情况，其最终膨胀率明显低于50，75 kPa的情况。而对于无荷膨胀，无论含水率高低，其曲线初始增速极快，明显高于有荷膨胀情况，并且在极短时间内就接近最终膨胀率并趋于稳定。为更进一步了解其膨胀特征，将其膨胀率与对数时间关系分别绘制于图3，4。

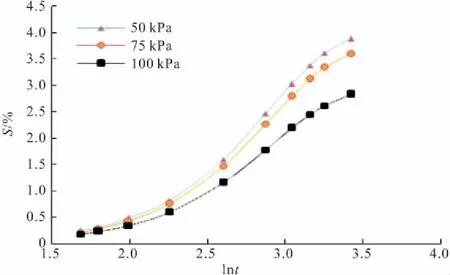
图3 不同压力下膨胀率与时间对数的关系(4#样)

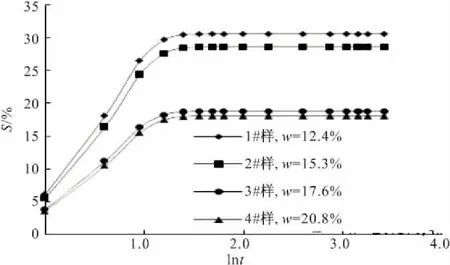
图4 无荷膨胀下膨胀率与时间对数的关系

从图3，4可以看出，有荷膨胀的膨胀线明显分为三个阶段：0～2 h膨胀速率不大(初始膨胀区)，随后持续增长(主膨胀区)，直至约44 h后才逐渐放缓并趋于稳定(二次膨胀区)。而无荷膨胀的膨胀线从一开始就持续增长，几乎只有两个阶段，并在不到1 h内就完成了95%以上的膨胀并趋于稳定。可以看出，不同情况下的膨胀速率有着非常大的不同。对于这种复杂的时程曲线，可以从膨胀土的膨胀机理分析确其曲线特征，从而讨论其曲线各阶段的物理含义。

2.2 膨胀土膨胀时程曲线特征分析

从微观角度来看，膨胀土的膨胀主要是依靠水分子与亲水膨胀矿物(如蒙脱石，伊利石等)结合后，在土粒内部的矿物晶体间形成双电层，使较大凝絮土粒之间发生膨胀，并剥落为较小的颗粒[20]。引申至宏观角度，双电层作用和凝絮土粒剥落机制将产生膨胀力和膨胀体积变形，增加膨胀土的体积和孔隙比，而其膨胀力和变形的发挥程度则受到上部荷载的限制。因此，水分子与进入土粒内部孔隙中的速度决定了膨胀土的膨胀速度，而膨胀土的最终膨胀量则主要由土体初始状态和力学边界条件所决定。

结合湘西膨胀土的试验结果，对膨胀土膨胀时程曲线各阶段变化的内部机理分析如下：对于图3的有荷膨胀情况，在上部压力约束下，膨胀土内部结合紧密，水分子进入土体内部孔隙较为困难，所需时间长，因此图3曲线第一阶段的膨胀速率较为缓慢；当膨胀发生后，土粒内部间相互排斥、剥落，内部孔隙增加，使得水分子能够更快地进入土粒内部并发生反应，从而图3第二阶段的膨胀速度明显增加。随着时间增加，土体不断吸水而趋于饱和，此时其内部孔隙已无法容纳更多水分，导致图3曲线第三阶段的膨胀速率逐渐放缓并趋于稳定。同时由于上部压力的存在，部分地抵消了膨胀力的发挥，限制了膨胀变形的发展，最终有荷膨胀在稳定阶段的最终膨胀率要低于无荷膨胀情况。而对于图4的无荷膨胀情况，其曲线第一阶段增速快，持续时间短；这是因为无荷膨胀缺少上部荷载约束，膨胀土颗粒间结合不如有荷膨胀紧密，水分子能够快速进入土粒内部孔隙，与膨胀矿物反应并达到稳定状态。因为无上部荷载约束，水分进入膨胀土粒的内部孔隙后，能够充分与膨胀矿物反应直至土体饱和，其膨胀曲线的稳定阶段膨胀率要高于有荷膨胀情况。

通过上述分析可以得出，对于有荷与无荷膨胀情况，其膨胀机制有所区别，而膨胀曲线增长速率是分阶段变化的，并且受到外部荷载的影响。而模型参数β为常数，不能用来描述曲线整体的膨胀速率，以下将通过数学分析的手段进一步阐明膨胀时程曲线各参数的物理含义。

3 膨胀时程曲线参数物理含义及确定方法

由前述，式(1)阐述了膨胀时程曲线的一般形式，令式中t→∞，可得S(∞)=α，这样，参数α可表述为最终膨胀率控制参数。此外，对式(1)求导可得：

S′(t)=αβe-βt

(2)

令式(2)中t=0，即得：

S′(0)=αβ

(3)

由式(3)可知，膨胀时程曲线的初始膨胀速率由α，β的乘积共同控制，而并非单独由β控制。为了明确β的含义，引入物理学中半衰期的概念，将膨胀时程半衰期定义为：膨胀土膨胀至最终膨胀率一半时所对应的时间，其数学形式可用式(4)表示。

(4)

式中：tα/2为膨胀半衰期，解式(4)可得：

βtα/2=ln2

(5)

由式(5)可知，β与半衰期的乘积为一常数，因此β即可表征膨胀时程曲线增长至半衰期的速率，β越小，膨胀时程曲线增长至半衰期的时间就越久。基于半衰期的概念就能确定参数：首先通过时程特征曲线的稳定阶段确定参数α；然后在曲线上标定出纵坐标为α/2的半衰期特征点(tα/2，α)，确定tα/2后即可根据式(5)计算β。如图5所示。

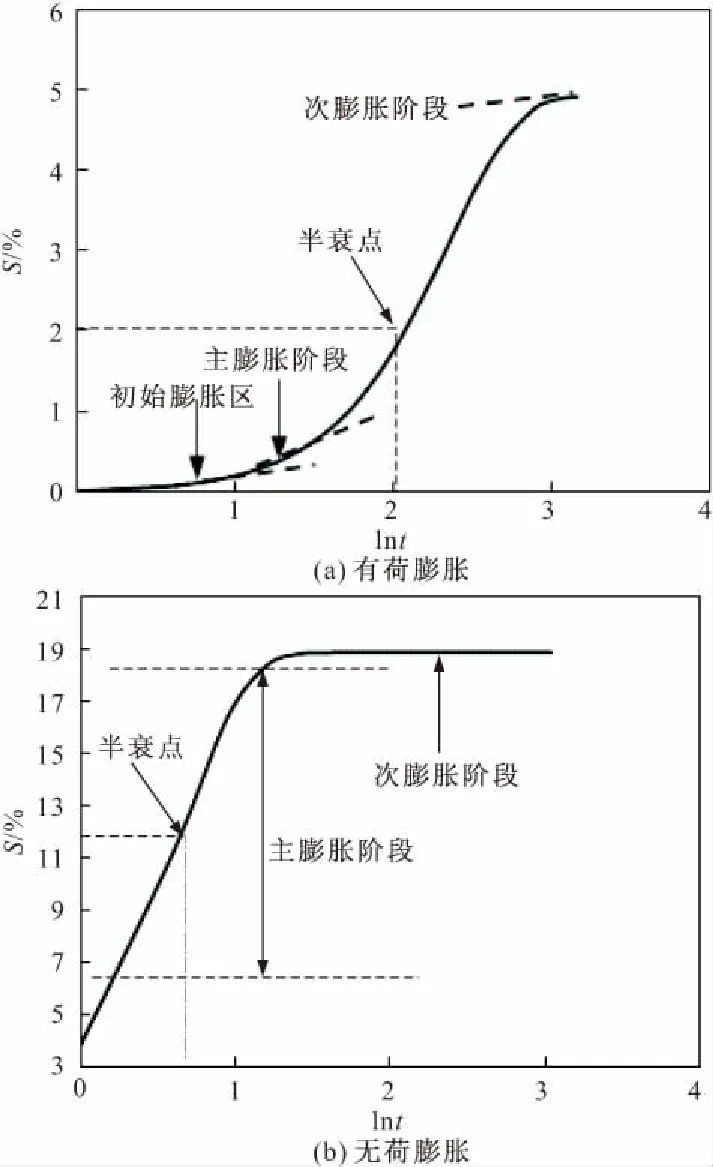
图5 膨胀时程特征线

为验证半衰期拟合的适用性，以3#样一维75 kPa与无荷膨胀试验的实测结果为基础，将本方法与最小二乘法的拟合结果进行对比，如图6，7所示。

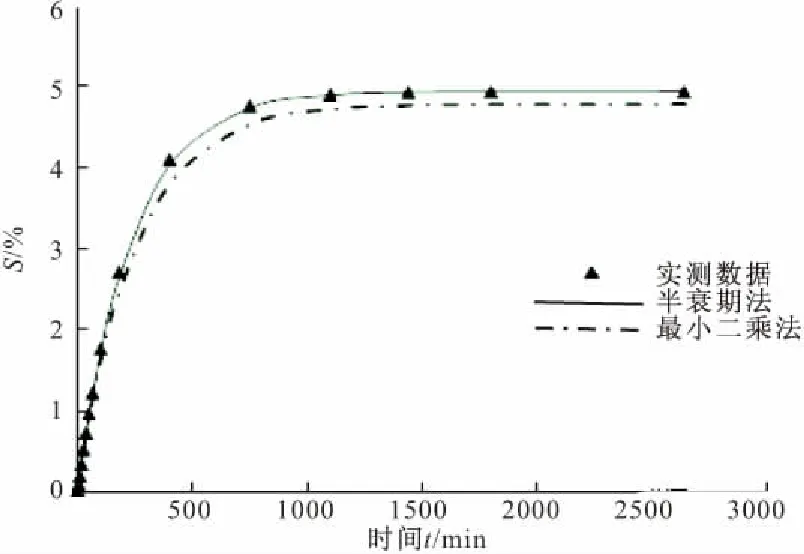
图6 75 kPa荷载对比曲线

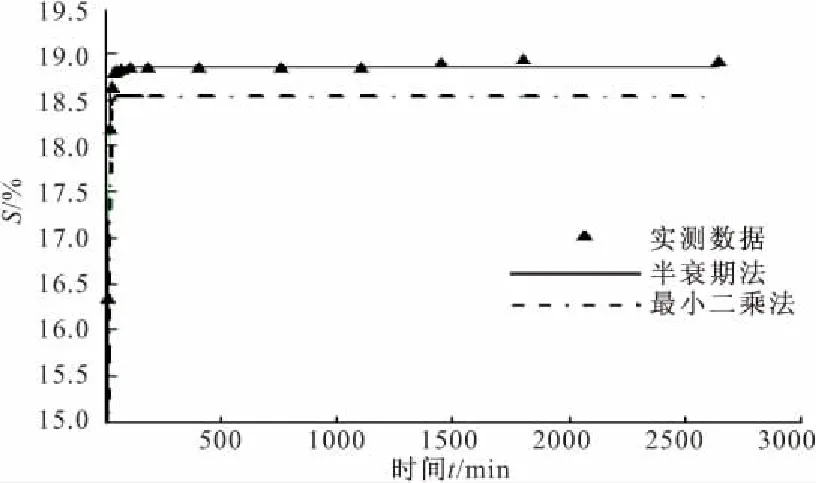
图7 无荷膨胀下时程曲线对比

从结果对比来看，对于有荷情况，两种方法都有较好的拟合效果。但对于无荷膨胀情况，半衰期拟合方法则更能捕捉其膨胀特征。其原因可解释如下：膨胀时程曲线的导数，即为其膨胀速率曲线，如式(2)所示。绘出无荷膨胀和有荷膨胀的速率曲线如图8所示。

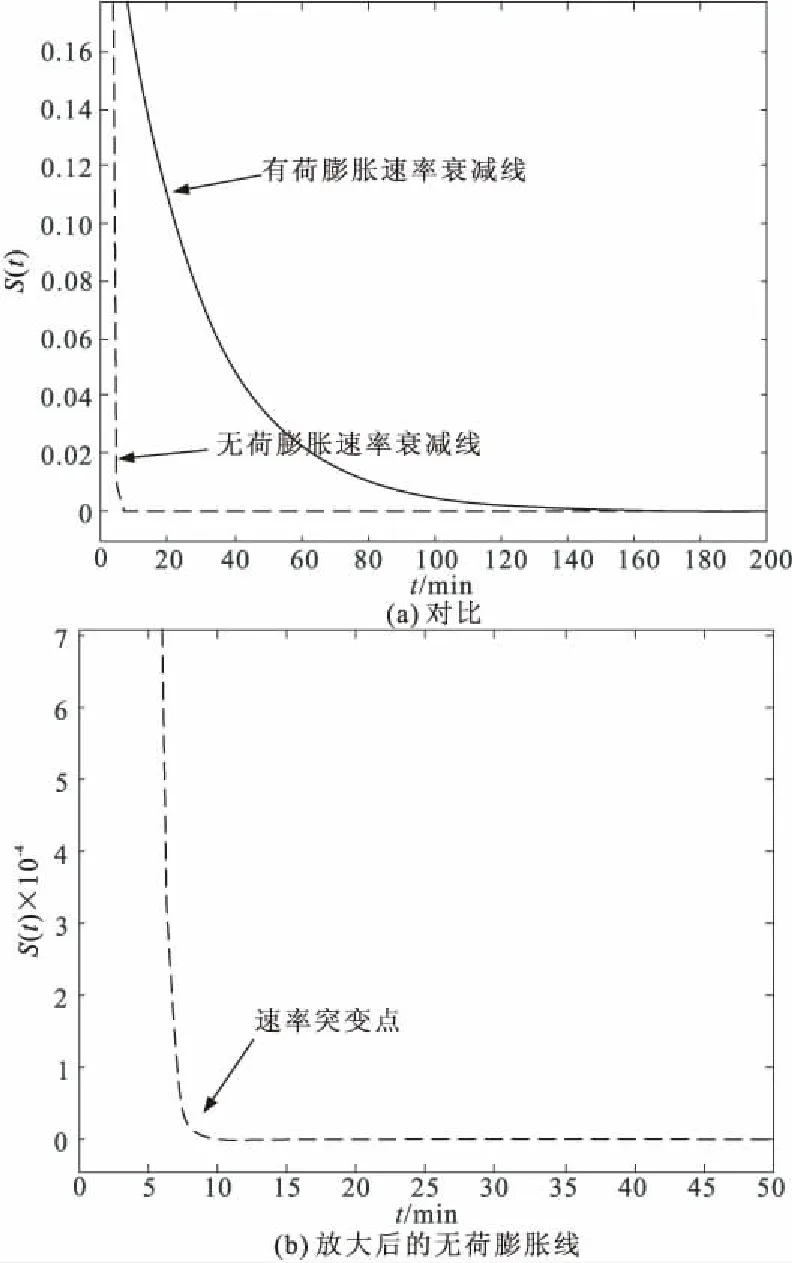
图8 膨胀速率曲线

从图8可以看出，有荷膨胀速率曲线非常平滑，而无荷膨胀速率曲线变化非常快，且具有“尖点”，即速率突变点。最小二乘法是通过将误差表示为导数求取曲线参数的[21]，对于较为平滑的有荷膨胀速率线，能较好的计算其误差。但对于具有速率突变点的无荷膨胀速率线，则难以捕捉这一特征。而无论是有荷膨胀还是无荷膨胀，都存在着半衰期，并且容易标定。因此，在模型参数含义和标定方法方面，基于半衰期的参数确定方法都要优于最小二乘法。

4 结 语

本文基于物理学中半衰期的概念，分析了有荷与无荷膨胀时程曲线的特征和参数含义，并给出了参数确定方法，最后与最小二乘法进行了对比，得出以下结论：

(1)有荷膨胀时程曲线大致可分为三个阶段：初始膨胀区、主膨胀区和二次膨胀区，其膨胀变形在主膨胀区持续变大，随后在二次膨胀区趋于稳定。而无荷膨胀的膨胀线从一开始就持续增长，几乎只有主膨胀区和二次膨胀区两个阶段。

(2)膨胀土膨胀的主要原因是水分进入土粒内部孔隙后，矿物晶体间形成双电层使得凝絮土粒发生剥落现象。有荷情况下水分进入土粒内部孔隙速度慢于无荷情况，其膨胀速率和膨胀程度也受到荷载限制。因此两种情况下膨胀曲线的速率和膨胀特征并不相同，这也是导致膨胀时程曲线参数物理含义不明确和难以确定的原因之一。

(3)基于半衰期的概念，膨胀土最终膨胀率可由参数α表示，而β表征膨胀时程曲线增长至半衰期的速率。α可由膨胀时程曲线的最终膨胀率确定，β可根据膨胀时程曲线的半衰点确定。

(4)对于有荷情况，半衰期方法与最小二乘法拟合的效果相差不大。但对于无荷膨胀情况，半衰期拟合方法则更能捕捉其膨胀特征。这是因为无荷膨胀速率曲线变化非常快，具有速率突变点，最小二乘法无法描述这一特性。因此，半衰期拟合法在表述参数含义和标定参数值方面都要优于最小二乘法。