基于非牛顿指数渗流的饱和黏土一维流变固结分析

刘忠玉，黄家涛，夏洋洋，张家超，崔鹏陆

(郑州大学 土木工程学院，河南 郑州 450001)

在饱和软黏土地区，地基土的固结和沉降问题向来都是学者们较为关注的问题之一[1]。而大量的试验表明，许多饱和黏土具有显著的流变性[2～6]，其中孔隙水的渗流也存在明显偏离达西定律的现象[7～11]。但传统一维Terzaghi固结理论并没有考虑这些因素，因此学者们便从上述两个方面开始对Terzaghi固结理论不断进行修正。在流变方面，Taylor等[2]首先引入Kelvin模型对一维固结试验中发现的蠕变现象进行了解释。随后先后有学者引入Maxwell[12]，Merchant[13]，Voigt[14]等元件模型对一维固结问题进行了分析。但此类元件模型是由基本元件组合而成，有时为了更好地模拟实际情况，需要组合较多的元件，这会导致本构方程参数多而复杂，给应用带来不便。于是，一些学者[15～19]便引入分数导数描述流变固结问题，或引入流变经验表达式对一维非线性流变固结问题进行探讨。同时，一些学者[20～23]建立或扩展了弹黏塑性理论，其中Yao等[23]考虑了土体的蠕变效应，将基于修正剑桥模型的统一硬化(Unified Hardening，UH)模型推广至可以考虑土体的流变特性，即考虑时间效应的UH模型。由于该模型能够描述土体的大部分变形特性，且参数少，物理意义明确，并可通过常规试验方便获取，所以已被引入到一维固结分析中，且进一步解释了传统固结理论所不能解释的现象[22,24,25]。另外，Liu等[26,27]对萧山黏土和香港海相黏土进行了相关的理论模拟表明该模型具有较广的适用性。

在非达西渗流方面，鄂健等[28～30]先后将Hansbo渗流和非牛顿指数渗流引入到一维固结分析中，证明了考虑非达西渗流的必要性。随后，时刚[31]在刘忠玉等[29]的基础上引入了Merchant流变模型。李传勋等[32]在考虑起始水力坡降渗流的同时，将四元件模型、Merchant模型、Maxwell模型及线弹性模型进行了对比，强调了同时考虑非达西渗流和流变效应的必要性。但上述依然是元件模型研究范畴。后来，刘忠玉等[25,33]先后在考虑Hansbo渗流的基础上引入了分数阶Merchant模型和考虑时间效应的UH模型，对一维固结问题进行了探讨，但对实际工程中施工荷载的影响未做分析。另外，在常用的非达西渗流模型中，Swartzendruber[9]提出的非牛顿指数渗流模型相比分段形式的Hansbo渗流模型，参数更为简单，也能较好地拟合Hansbo[7]的试验数据。

因此，为进一步深入研究饱和黏土的流变固结特性，本文在考虑非牛顿指数渗流和变荷载的同时，引入考虑时间效应的UH本构模型，对一维固结方程进行重新推导，并用有限体积法进行了数值求解，然后着重分析了次固结指数、非牛顿指数、施工工期及外荷载对一维流变固结进程的影响。

1 流变固结方程的推导及求解

1.1 考虑时间效应的UH模型介绍

考虑时间效应的UH模型一维应力应变增量型表达式为[22,23]：

(1)

(2)

(3)

(4)

式中：Cs为回弹指数；Cc为压缩指数；e0为初始孔隙比；Cα为次固结系数；t0为单位时间；tα为老化时间；M和Mf分别为临界状态应力比和潜在破坏应力比，即

(ta+t0)/t0=R-α

(5)

(6)

(7)

式中：χ=M2/[12(3-M)]；α=(Cc-Cs)/Cα；φ′为土的有效内摩擦角；R为超固结参数，即

(8)

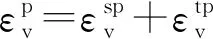
1.2 问题的描述

有一厚为H的均质饱和黏土地基(见图1)，顶面透水，底面不透水，且在初始有效应力σ′0作用下地基已完成固结。假设地基中孔隙水和土颗粒不可压缩，且只考虑地基中竖向的渗流和变形。现于地基顶面施加施工荷载p(t)(见图2)，荷载初值为0，终值为p0。p(t)的线性表达式为：

(9)

式中：tc为工期。

假定渗流用式(1)所示的基于非牛顿指数描述的非达西渗流公式来表达[9]，即：

v=-k[i-i0(1-e-i/i0)]

(10)

式中：v为渗流速度；i为水力梯度；k为渗透系数；i0为v-i曲线渐近线的截距，称为非牛顿指数；e为孔隙比。

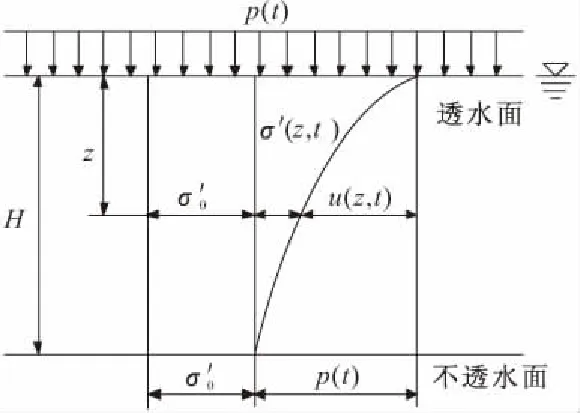
图1 分析模型

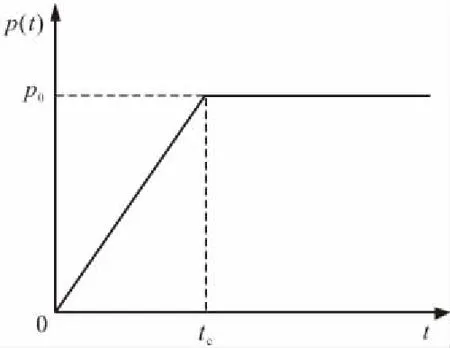
图2 施工荷载随时间变化关系曲线

设在地基深度z处，时刻t的有效应力和超静孔隙水压力分别为σ′(z,t)和u(z,t)，二者的关系可表示为：

σ′(z,t)=σ′0+p(t)-u(z,t)

(11)

在式(11)中对z求偏导，可得：

(12)

考虑渗流的连续性：

(13)

结合式(1)(10)(12)(13)可得控制方程为：

(14)

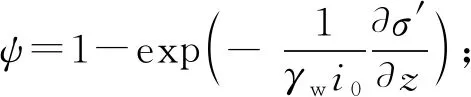
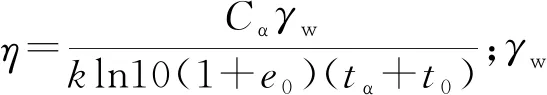
与图1对应的初始条件和边界条件分别为：

σ′(z,0)=σ′0，0≤z≤H

(15)

σ′(0,t)=p(t)+σ′0

(16)

(17)

1.3 方程的有限体积法求解

由于式(14)是非齐次偏微分方程，求其解析解很困难，所以本文借鉴刘忠玉[29]等引入的有限体积法对其进行求解。

首先把饱和黏土层从上到下均分为n层，每层厚Δz，每层中点为该层的控制节点；以步长Δt对时间离散，那么在Δt时间间隔内(从时刻tj到tj+1)，第m个控制节点的方程为：

(18)

式(18)进一步展开为：

(19)

式中：下标L，N分别代表该控制体积的下、上边界点。

对式(19)中有效应力关于时间t和空间z的偏导数进行差分，可得：

(20)

为便于对上式等号左边积分，一般取时刻tm和tm+1的有效应力加权平均值进行计算。如取时刻tm和tm+1的权重分别为0和1，即为全隐格式。则式(20)变为：

(21)

1.4 初始条件和边界条件的处理

初始条件式(15)可离散为：

(22)

对控制体积1，考虑透水边界式(16)，则：

(23)

式(23)可离散为：

(24)

对于控制体积n，考虑不透水边界式(17)，即：

(25)

将式(25)代入式(19)，然后再离散可得：

(26)

至此，式(21)(22)(24)(26)构成的方程组是封闭的，用迭代法求解各点的有效应力。然后，可得各点的超静孔隙水压力为：

(27)

为表示地基的孔压消散速率，引入按孔压定义的固结度，即：

(28)

同时按式(29)计算地基的沉降：

(29)

2 解法及流变模型的验证

2.1 解法验证

根据上述解法，编写相应的Fortran程序，并将本课题退化为与胡晶[22]一样的课题，即达西渗流下的UH模型。参数取值如下：i0=0，R0=0.95，M=1.112，Cα=0.0108，Cs=0.0131，Cc=0.0217，H=1 m，σ′0=10 kPa，p0=90 kPa，e0=0.53，k=3.63×10-7m/min，tc=0,n=50，Δz=0.02 m，Δt=0.0001 min，迭代误差为10-7，计算结果见图3。从图3中可以看出本文的计算结果和胡晶的吻合很好。

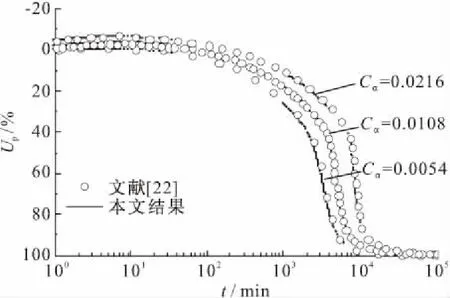
图3 本文理论解与胡晶[22]理论解对比

2.2 UH模型的验证

为进一步验证UH模型的适用性，取河南某地的黏土进行试验。取样深度为地表下2.5 m。为了保证土体的均匀性以及方便试验对比，参照Yin[4]的方法，首先将土样加水制成泥浆，并通过0.075 mm的筛子以滤去杂质，然后加压制成重塑土样，其土工参数见表1。最后，在高压固结仪中进行了一维流变固结试验，沉降S与时间t的关系见图4。按上述理论对试验结果进行模拟时，考虑到固结试验中试样厚度仅有2 cm，非达西渗流对固结过程的影响难以体现[29]，这里按达西渗流进行分析，即令i0=0；UH模型相关参数如压缩指数Cc、次固结指数Cα和回弹指数Cs均根据试验结果取值，而渗透系数k和初始超固结参数R0根据试算取值，有效内摩擦角按经验取值φ′=20°(M=0.772)，如表2所示。理论曲线见图4。从图4可看出，试验结果与理论预测值吻合较好。

表1 试样的基本参数

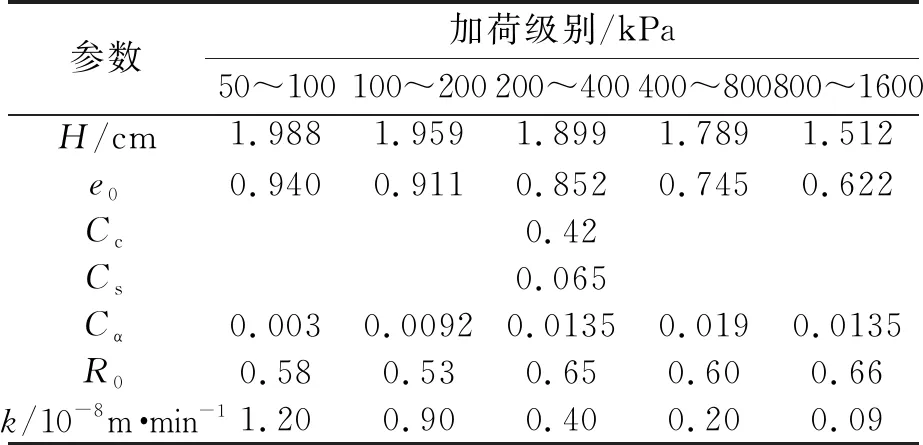
表2 参数的选取

图4 沉降理论预测值与试验结果对比

3 参数分析

目前，基于非牛顿指数渗流的试验较少，其参数i0的规律还不明朗，下面单因素分析时取i0=3.0。同时，在李西斌[34]的基础上，选取其他分析参数如下：R0=0.5，M=0.772，Cα=0.03，Cs=0.08，Cc=0.45，H=5 m，σ′0=50 kPa，p0=150 kPa，e0=1.5，k=3.0×10-7m/min，tc=90 d，并取n=100，Δz=0.05 m，Δt=0.0001 min，迭代误差为10-7。

3.1 次固结系数Cα对流变固结的影响

UH模型中表示土体黏滞性的指标是次固结系数Cα，它对地基流变固结过程的影响如图5所示。图5a是不同Cα值下地基底部不排水面处的孔压随时间的变化曲线。从中可看出，在施工阶段，该处的孔压都随时间而累积。当不考虑土体黏滞性(Cα=0)时，可认为是施工荷载增加的结果。但是当考虑土体黏滞性(Cα>0)时，该处的孔压可以大于对应时刻的施工荷载值，这就不能仅仅用施工荷载增加来解释。另外，在竣工后，当Cα=0时，孔压将随时间增长而消散；但当Cα>0时，竣工后一定时期内，孔压还会继续累积，甚至超过最大荷载值，达到极值后再随时间增长而消散。此外，图5a还表明，Cα越大，孔压达到的极值就越大，达到极值需要的时间也越长。这种现象与“曼德尔效应”相似，但实质上是不同的：曼德尔效应仅出现在二维或三维Biot固结中，而在太沙基固结理论范畴，以及不考虑黏滞性的一维固结分析或线性弹黏性一维固结分析中是不会出现的。正如Yin[20]、胡晶[22]、刘忠玉[25]等学者的分析，这种现象源于饱和黏性土的黏滞性或主次固结耦合机制。刘忠玉[25]等称之为“类曼德尔效应”。

次固结系数Cα对地基平均固结度Up的影响规律见图5b。从中可看出，增大Cα值，将使得固结度减小，地基孔压整体消散变慢。这与一般的线性弹黏性固结分析结果[12,14,19,32,33]类似。但是，图5b还表明，当考虑土体黏滞性(Cα>0)时，在施工阶段甚至竣工初期，固结度为负，这说明地基内较大范围内的孔压累积都超过了地面施工荷载值。

图5c是次固结系数Cα对地基沉降的影响曲线。图5c表明，当Cα=0时，地基沉降会随着孔压的消散而逐渐趋于稳定；当Cα>0时，地基沉降会在孔压完全消散后继续发展，并且Cα越大，地基沉降就越大。

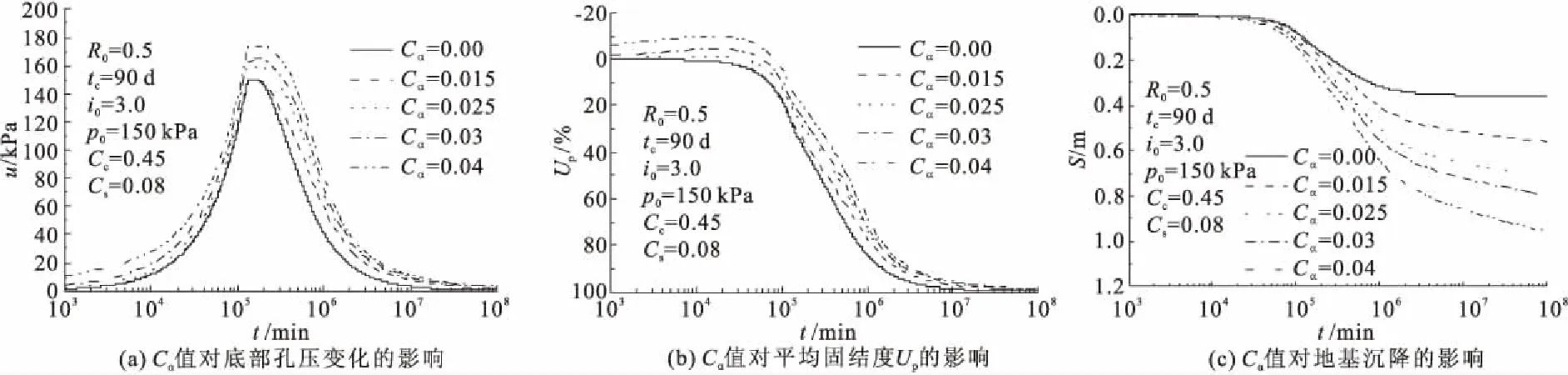
图5 Cα对流变固结的影响

3.2 施工工期tc对流变固结的影响

施工工期tc对地基流变固结的影响见图6。其中图6a表明，与瞬时加载相比，延长施工工期将使得固结前期的地基沉降变慢。但随着时间的增长，各条曲线基本趋于重合，即施工工期不会对后期沉降造成影响。另外，图6b所示的固结度随时间的变化曲线与图6a规律相似。也就是说，施工工期对地基孔压的整体消散只在施工期及竣工初期有较大的影响，且工期越长，该期间孔压消散越慢。故在实际工程中可以通过合理安排施工工期来控制施工期和竣工初期的地基沉降速率和孔压消散速率。

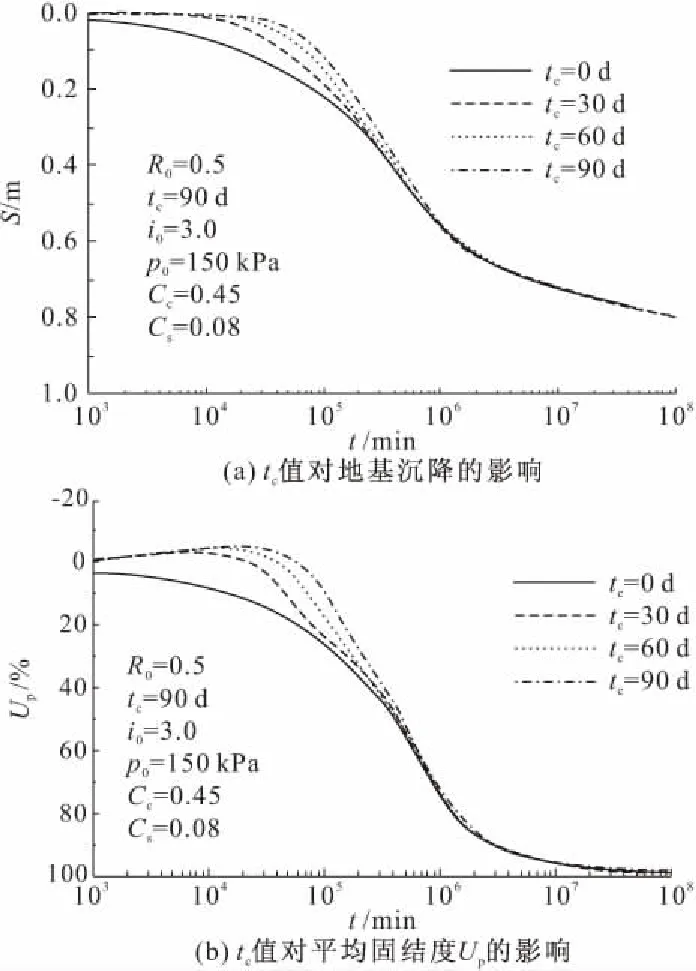
图6 tc对流变固结的影响

3.3 施工荷载p0对流变固结的影响

图7反映的是施工荷载p0对地基流变固结的影响。图7a和图7b表明，施工荷载p0越大，地基的沉降就越大，地基中孔压的整体消散也就越快。这与黄文熙教授[1]的结论一致，也是太沙基固结理论和线性黏弹性理论所不能预测的。图7b还表明，在固结初期，施工荷载p0越小，固结度出现负值的时间就越长，其绝对值也越大。这说明地基中较大范围内出现了孔压累积现象。这也可与图7c中的地基底部不排水面处孔压随时间的变化曲线相互印证。图7c表明，施工荷载p0越小，前期的地基中的“类曼德尔效应”就越显著，而后期的孔压消散也越慢。这与李传勋[30]的施工荷载越大，孔压消散越快的结论一致。

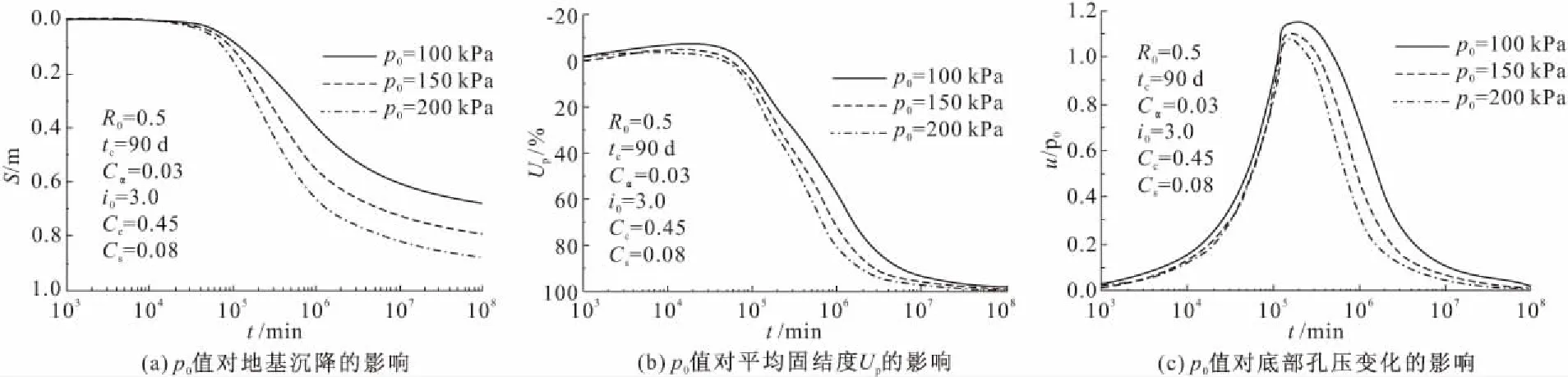
图7 p0对流变固结的影响

3.4 非牛顿指数i0对流变固结的影响

图8为不同非牛顿指数i0值下的流变固结曲线。从图8a中可以看出，非牛顿指数i0值并不影响地基沉降变形的最终值，但却极大地影响着地基的沉降进程。与达西渗流(i0=0)相比，非牛顿指数越大，地基同一时刻的沉降就越小，达到同一沉降值需要的时间也越长。

图8b描述了非牛顿指数i0对平均固结度Up的影响。与李传勋[30]结果相似的是，图8b表明，非牛顿指数渗流下的地基孔压的整体消散要慢于达西渗流，且非牛顿指数i0越大，地基孔压的整体消散就越慢。

图8c描述的是不同i0值下地基底部不排水面处孔压随时间的变化规律。图8c表明，与达西渗流相比，非牛顿指数i0使得“类曼德尔效应”更加显著：随着i0的增大，孔压极值有所增大，且达到孔压极值需要的时间也相应延长。纵观整个流变固结过程，在施工阶段，孔压累积的速率并没有因为i0的不同而有太大的差别，但在竣工后孔压的消散却随着i0的增大而减慢。这表明，非牛顿指数i0对地基流变固结的影响主要体现在竣工后。

图8 非牛顿指数i0对流变固结的影响

4 结 论

本文在考虑时间效应的UH模型的基础上，结合非牛顿指数渗流，重新推导了饱和黏土一维固结控制方程，并分析了在施工荷载作用下黏土地基的流变固结特性，得出如下结论：

(1)土体的黏滞性是引起“类曼德尔效应”的主要原因。与不考虑黏滞性相比，随着次固结指数的增大，地基沉降速率变慢，且同一时刻地基的沉降量增大。即不考虑黏滞性的影响会低估地基的沉降变形量，高估地基的沉降变形率。

(2)施工工期仅对施工期和竣工初期的地基沉降和孔压消散有影响。随着施工工期的延长，施工期和竣工初期的地基沉降变慢。

(3)地基固结进程明显受施工荷载大小的影响。随着施工荷载的增大，“类曼德尔效应”趋于不明显，且竣工后期地基内孔压的整体消散也变快。

(4)非牛顿指数渗流增强了竣工初期的“类曼德尔效应”，延缓了地基的沉降和竣工后期地基内孔压的整体消散，但不影响其最终沉降量。