基于质量验收模型的策略分析与评估
2020-07-22易晨光王淑嫱
易晨光,谭 燕,王淑嫱
(湖北工业大学 土木建筑与环境学院,湖北 武汉 430068)
建筑业是我国国民经济的支柱产业,建筑质量牵涉广大人民切身利益,影响国民经济的持续、稳定发展。目前,随国家供给侧改革逐步深化,政府对建筑工程质量监管的力度不断提高,但施工过程中存在一些质量问题,较为常见的有裂缝、空鼓、阴阳角开裂等[1]。从施工角度看,工程质量问题主要与两方面有关:其一是由于施工单位与监理单位为寻求更高的经济效益,选择企业合谋相互包庇,促使施工过程中偷工减料;其二是监理单位缺少科学有效的管控方法,不合理的管理力度,不仅令工程质量难以保证,经济效益也会随整改次数增多而降低。因此,研究质量监管中的验收过程对提高工程质量具有重要的现实意义。针对建筑工程质量验收环节,许多研究致力于提高从业人员专业水平,认为一定水平的专业能力和施工经验能帮助提高施工质量[2]。也有研究[3,4]认为工程质量受监理单位检查成本、建设单位奖罚力度等管理因素影响较大,制定有效的管理策略至关重要。Brito等[5]通过对香港建设工程项目的研究,发现质量问题主要来源于工程环境、管理情况和合同条款等。Chan等[6]在研究报告中指出,项目管理团队的管理行为、建设团队的领导力和客户对质量的重视等是影响工程质量的主要因素。针对专业水平和管理策略的影响,若从有限理性角度出发,将博弈理论运用到验收过程中,能为策略选择提供有效依据。
近年来,博弈理论被广泛应用于策略选择、行为采纳、风险评估等[7~9]问题。经典博弈理论从完全理性出发,假设博弈过程中的当局者都在追求最大利益[10]。而演化博弈理论在经典博弈理论的基础上对时间微分,研究动态变化过程[11]。国内对博弈理论的应用起步较晚。张飞涟等[12]用经济期望分析验收过程中参与双方纯策略纳什平衡和混合策略纳什平衡,对质量失控的负面效应进行了初步研究。王晓燕等[13]以演化博弈论为基础,运用复制动态方程分析验收过程中的策略选择,认为建筑工程质量验收过程是一个循环反复的博弈过程并不存在纳什平衡。张攀和郭聖煜[14]引用系统动力学模型对各影响因素进行仿真模拟,确定影响验收模型的关键内部因素。目前,在各博弈分析中,以微分方程稳定性原理确定策略稳定状态已经得到广泛应用[15,16],但针对博弈策略变化趋势的研究略有不足。在建筑工程验收环节,对钢筋、模板、混凝土等工序进行检查时,因楼层层数有限,博弈次数仅十到五十次不等,可能双方都未达到策略稳定,博弈就已经结束。该情况表明,短期博弈中,过程分析远比结果预测重要。
本文采用演化博弈理论分析建设项目质量验收过程,构建施工单位与监理单位博弈模型,从策略变化趋势出发,以博弈路径和工程质量作为衡量标准,借助Matlab数值仿真,对各种博弈变化情况进行优劣评估,通过最优策略调整奖罚力度,保障工程质量。
1 建立质量验收模型
1.1 基本理论假设
为建立有限理性模型,在认为施工单位具备一定的管理能力和丰富的经济知识前提下,令监理单位为“局中人1”,施工单位为“局中人2”,做出如下假设:
假设一:监理单位在施工监督过程中由于资金和人力因素影响,非关键工序采取抽检模式,检查工序中有两种策略选择:a1:检查合格,继续下一步工序;a2:检查不合格,队伍进行整改。设选择策略a2情况下,复检合格率为100%,每次检查的成本期望为n。
假设二:由于施工单位管理力度参差不齐,施工单位有两种策略选择:b1:按规范要求施工;b2:不按规范要求施工,同时规定监理单位验收不合格。设选择策略b2情况下,施工单位需要缴纳罚金为i,并按照监理单位要求逐一整改,整改过程中产生的费用及工期延误损失总计为g,假设施工单位经过整改一次后能达到监理方要求并进入下一步工序。施工单位选择策略b1的经济效益为m1,施工单位选择策略b2的经济效益为m2。
假设三:若监理单位选择不检查,施工单位选择违规施工,存在一定的质量风险期望E,若监理单位检查合格,或施工单位整改完成,则不存在质量风险。
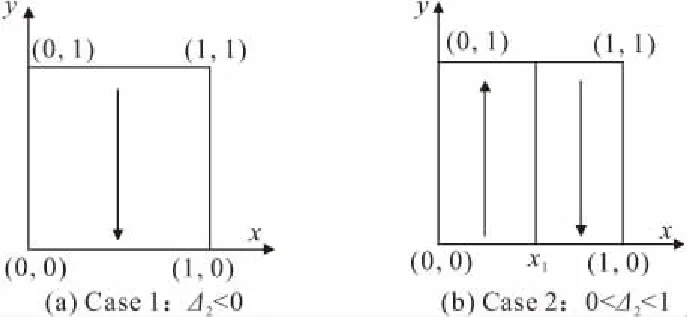
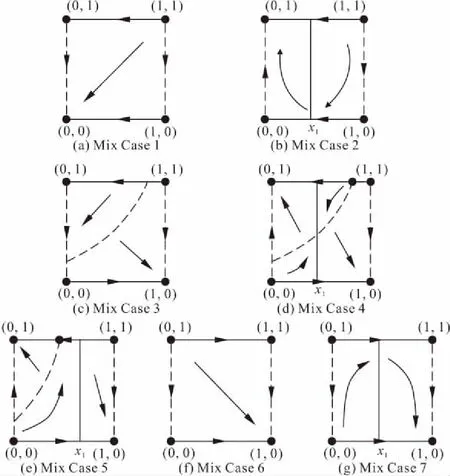
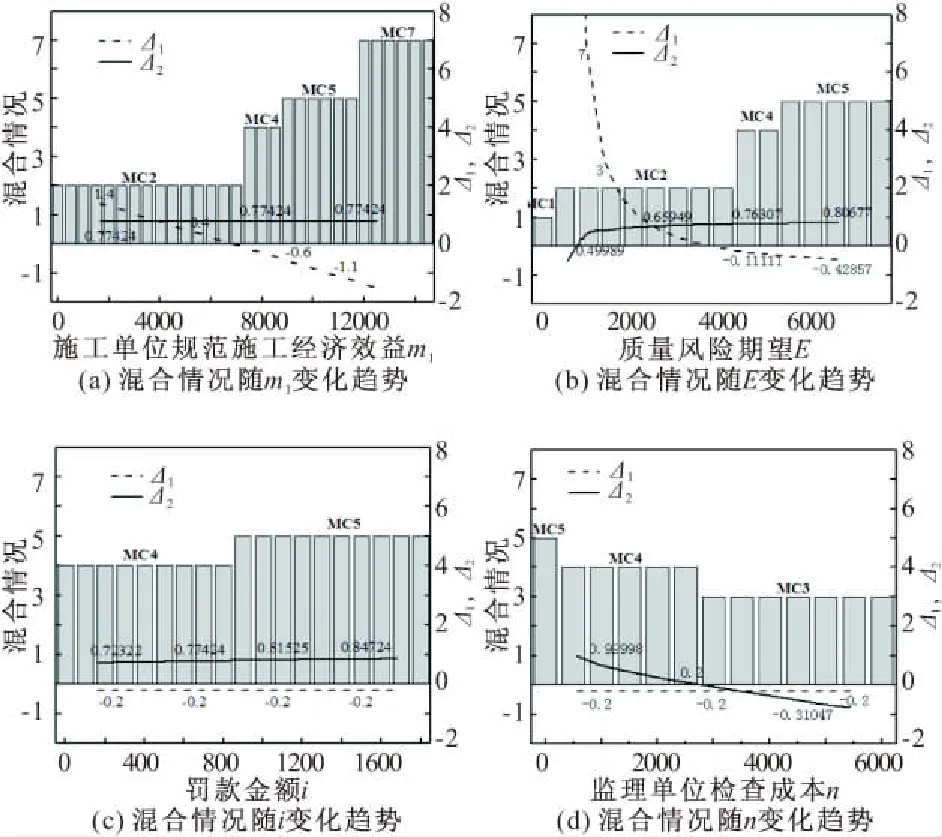
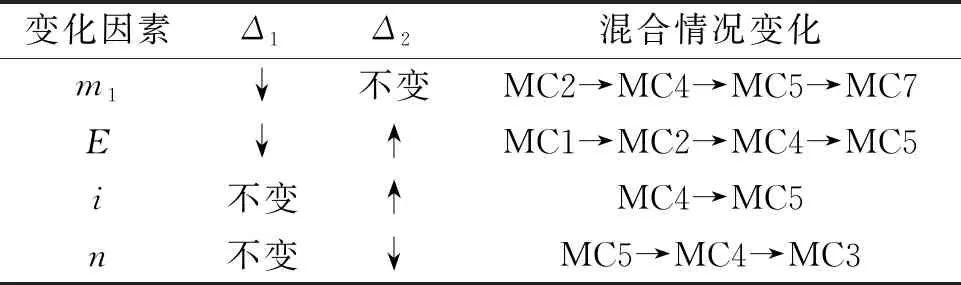
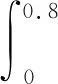
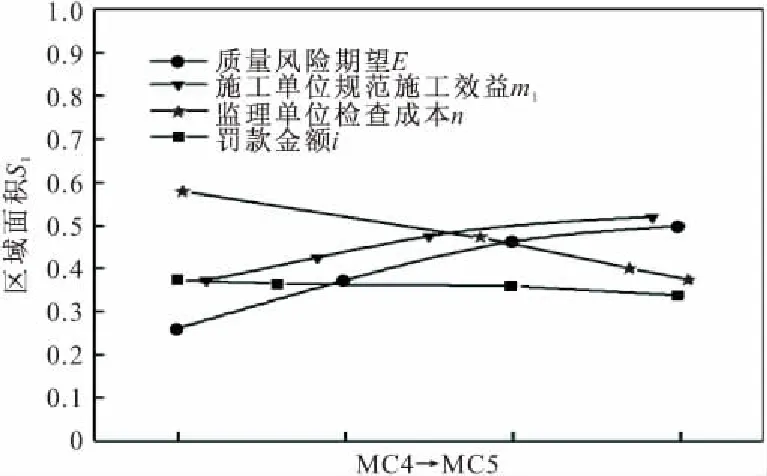
假设四:施工单位按照规范要求施工的概率为x(0 根据以上假设,局中人1的策略空间S1中有T1(主动检查(质量合格)),T2(主动检查(质量不合格)),T3(不检查(存在一定的质量风险))等三种策略,即S1={T1,T2,T3}。局中人2的策略空间S2中有U1(按规范要求施工),U2(不按规范要求施工)两种策略,即S2={U1,U2}。 通过S1,S2的策略空间计算各博弈策略相应比例,得质量控制博弈矩阵,如表1所示。 表1 质量验收博弈矩阵 Ua1=yf(x)m1+y(1-f(x))(m1-i-g)+(1-y)·m1=y(i+g)(x-1)+m1; Ua2=yf(x)(m2-E)+y(1-f(x))(m2-i-g)+ (1-y)(m2-E)=(xy-y)(i+g-E)+m2-E; (1) (2) 式(1)(2)反应了施工单位与监理单位策略选择的速度和方向,当dy/dt=dx/dt=0时为策略平衡状态,表示策略不再发生改变。 在复制动态方程的基础上对施工单位进行分析,令dx/dt=0,得x=0,x=1或y=(m2-m1-E)÷[E(x-1)]。设Δ1=(m2-m1-E)/E在定义域(0,1)内,施工单位规范施工比例x随时间变化趋势存在3种情况,见图1(图中任一时刻的博弈状态都对应平面区域内某一点,将该点简称为变化因子)。 图1 施工单位规范施工比例x随时间变化趋势 Case 1中Δ1>0,m2-m1>E,质量风险期望较小,低于施工单位效益差,施工方规范施工比例不断降低。 Case 2中-1<Δ1<0,m2-m1 Case 3中Δ1>-1,m1>m2。该情况说明,当违规施工所得经济效益低于规范施工时,施工单位会逐步提高施工质量。 综上分析,施工单位博弈平衡主要受质量风险期望与效益差影响。施工单位在非关键工序中出于经济效率考虑,很难保证施工质量。而关键工序中工程质量受监理单位检查比例影响趋于两极分化。 对监理单位复制动态方程进行分析,令dy/dt=0,解得y=0或y=1或x满足等式Ex2+(n-i-2E)x+E-2n+i=0,设方程的解分别为x1,x2(x1 (3) 由式(3)可知x1<1 不能以貌取人的道理你知道、我知道、拿石头打小鸟的死小孩也知道,所以我喜欢的女生不一定要长得漂亮,只要让我有感觉就好。只不过让我有感觉的女生总是长得很漂亮。 图2 监理单位检查比例y随时间变化趋势 根据图2中监理单位变化趋势,施工单位规范施工比例高于Δ2时,监理单位检查比例降低,低于Δ2时,监理单位检查比例提高。Δ2是决定监理单位检查比例变化的关键因素,也代表了监理单位检查标准。 由于施工单位规范施工比例x与监理单位检查比例y是同一区域内的变化情况,可以将两个 变化趋势反应到同一坐标系中,得到混合变化趋势图。经计算,混合变化趋势图共7种,见图3(图中,实线为监理单位策略稳定状态,虚线为施工单位策略稳定状态,实线与虚线的交点为混合情况下的平衡点)。 图3 施工单位与监理单位复合变化趋势 由图3可知,博弈过程因项目参数影响会出现多个平衡状态。当平衡状态受外界干扰发生微小偏移,能重新回到原平衡状态的平衡点为稳定平衡点。各混合情况稳定平衡点见表2。 表2 混合情况稳定平衡点 对比MC1,MC2,由于Δ1>0,项目质量风险期望较低,施工单位最终演化为完全违规施工,监理单位质量管理行为失效。MC3,MC4,MC5中-1<Δ1<0,项目质量风险较高。MC3的演化结果为施工单位规范施工,监理单位不进行检查,是较为理想的博弈趋势。针对MC4,MC5两种变化趋势,x1左侧变化区域内,监理单位检查比例提高过快会促使该区域内变化因子稳定于点(0,1),不利于施工质量,x1右侧区域监理单位检查比例不断下降,下降速度越快,稳定于点(1,0)的比例越高,监理单位提高检查比例不宜变化过快,而降低检查比例时越快越好。MC6,MC7中Δ1<-1,施工单位规范施工能获得更高的经济效益,监理单位检查标准Δ2仅影响自身策略选择。MC6,MC7的平衡状态有利于建筑工程施工质量,建议业主单位在结算工程价款时,在以往按量计价的基础上增设一定权重的施工情况附加价款,使施工单位规范施工能获得更高的经济效益,实现MC6,MC7中的良性循环。 在微分方程稳定性计算中,Friendman[18]提出通过判断雅克比矩阵的行列式和迹,可以直接确定稳定点,便于验证变化趋势图中平衡点的稳定情况。由于施工单位与监理单位博弈过程中并不存在具有普遍代表意义的稳定平衡点,不同项目参数的博弈情况大不相同。为分析项目参数的影响情况,用建筑工程中某层400 m2楼板混凝土浇筑为例。以5000 元质量风险期望,500 元罚款,2000 元额外损失作为项目管理参数,见表3。 表3 某层混凝土楼板浇筑项目管理参数 元 经计算,该项目验收过程满足MC4中博弈情况,除四个角部平衡点外还有边界平衡点(0.8,1)及内部平衡点(0.76,0.85)。为确定各平衡点稳定性,式(1)(2)分别对x,y求偏导,得雅可比矩阵: 将项目基本参数带入雅克比矩阵为: 当雅克比矩阵的行列式Det(J)>0,迹Tr(J)<0时,为系统稳定点。经校核,六个平衡点中仅(0,1)和(1,0)是稳定平衡状态,对数据进行验算后发现边界平衡点与内部平衡点任何情况下都不可能是系统稳定点,博弈终点仅出现在(0,0),(0,1),(1,0)三点之中,符合MC4变化趋势。 结合该案例,分别放大或缩小项目参数m1,E,i,n,判断Δ1,Δ2的变化情况,确定混合博弈情况的变化趋势(如图4)。各参数变化过程从0增大至无穷大时,混合趋势变化如表4所示。 图4 混合变化趋势随四种项目参数变化情况 表4 混合情况变化趋势 在假设一的基础上,施工单位不按规范施工,经一次整改后,也能通过验收。但该行为会产生极大的质量隐患。从工程质量考虑,认为平衡于点(1,0)的混合情况质量评估均高于平衡于点(0,0)与(0,1)的混合情况;从经济成本考虑,博弈路径出现往复时,会延长博弈周期,提高博弈成本。综上所述,对该项目可能发生的七种混合博弈情况进行优劣对比得:MC6>MC3,MC7>MC4,MC5>MC1>MC2。 MC4与MC5两种混合情况无法直接从趋势变化比较经济成本或工程质量情况,因此借助 Matlab软件,以趋近于0的时间精度t分别对式(1)(2)进行迭代赋值,模拟策略演化路径。将平衡于点(1,0)的区域面积为S1作为衡量标准评估工程质量。该项目博弈路径如图5a,插值法细化边界后如图5b。 图5 楼板浇筑项目策略演化路径 三阶多项式拟合变化边界得: y=3.70203x3-2.14447x2+0.6802x-0.07257,R2=0.99。 平衡于点(1,0)的区域面积为S1为: 出于罚款力度考虑,当罚款金额依次增大,高于800 元时,MC4→MC5,边界变化如图6。 图6 罚款金额与变化边界 由图6所示罚款金额由500 元提高至2000 元的过程中,变化边界不断向右偏移,平衡于点(1,0)的区域面积S1略有减小。基于罚款金额i考虑MC4优于MC5。 图7 MC4→MC5过程区域面积S1变化趋势 同样对施工单位规范施工经济效益m1、质量风险期望E、监理单位检查成本n分析,得如图7所示变化趋势。其中E,m1在MC4→MC5的过程中S1面积变大,施工质量提高,而监理单位检查成本n对应的S1减小,工程质量水平降低。因此。基于E,m1考虑,MC5优于MC4;基于监理单位检查成本n考虑,MC4优于MC5。 根据表4中混合情况变化过程与图4,6,7所示评估标准,提出如下改进意见: (1)若建设单位对工程质量有较高要求,可设置奖励机制,当规范施工经济效益高于违规施工时,如图4a中MC4→MC7,质量隐患必然减少; (2)罚款力度对当前项目来说影响较小,罚款金额超过800 元时,如图4c中MC4→MC5,工程质量略有下降; (3)建设单位可适当降低监理单位合同价款,当施工单位与监理单位的管理人员都具备较高的专业水平时,施工单位能自发保证施工质量,从而监理单位可适当降低检查比例以节约成本; (4)初始博弈策略对博弈路径和博弈结果影响极大,若项目开始时施工单位就以高标准规范施工,不仅能提高经济效益,更能保障工程质量。 本文构建施工单位与监理单位验收模型,运用演化博弈理论,比较五种单向变化趋势和七种混合变化趋势,评估不同博弈过程工程质量水平,得到以下结论: (1)施工单位规范施工情况主要受经济效益和质量风险影响。在关键工序中施工单位由于较高的质量风险,会提高规范施工比例。在非关键工序中,监理单位检查比例与惩罚力度对施工单位影响较小。 (2)针对不同质量风险的工程项目,以博弈成本和工程质量作为衡量标准,评估混合变化情况,能科学有效地设置奖励机制,调整惩罚力度。 (3)验收博弈初始阶段的行为策略对博弈结果影响较大,若施工单位入场时就以较高的质量标准施工,整体工程质量都会有所提高。 施工单位复制动态方程构建过程中抵消了额外损失价款g,这表示基于复制动态方程的理论体系,该变量不会干扰博弈过程。但实际情况是施工单位额外损失g会提高施工成本,必然影响博弈状态。该矛盾说明复制动态方程在研究某些管理参数时存在一定缺陷,后续研究考虑为复制动态方程增设调整系数,以满足更高的理性层次。1.2 策略集合与博弈矩阵

2 博弈双方动态趋势分析
2.1 构建博弈双方复制动态方程
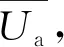
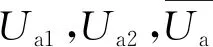
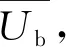
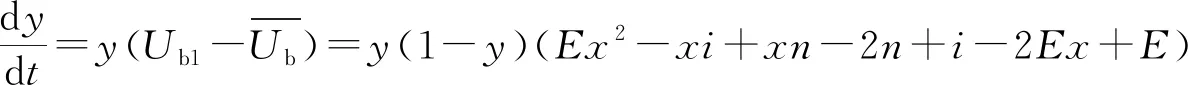
2.2 施工单位与监理单位单向策略变化趋势分析

2.3 混合策略变化趋势分析

3 工程案例分析
3.1 数值校核与仿真

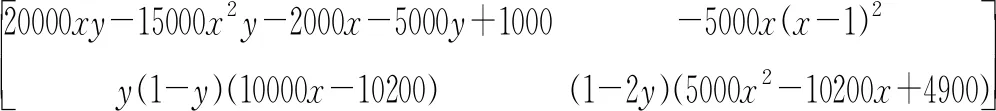
3.2 混合情况评估与对策建议

4 结 论
