连续排水边界下考虑指数渗流和土体自重的一维固结分析

宗梦繁，叶超，梁荣柱,2,3，梅国雄,2,3，杨晓燕，吴文兵,2,3

（1.中国地质大学工程学院，湖北武汉，430073；2.广西大学土木建筑工程学院，广西南宁，530004；3.广西大学广西防灾减灾与安全工程重点实验室，广西南宁，530004）

土体特性、土中渗流形式、排水边界条件以及作用于土体的外荷载形式等复杂，导致实际工程中土的固结规律非常复杂。传统固结理论通常假定土体中水的渗流服从达西定律，但一些黏土中的渗流形式可能为非达西渗流[1-3]，因而，有必要对考虑非达西渗流的土体固结问题进行研究。

在固结理论中常用的非达西渗流形式主要是Hansbo 渗流模型[1]、指数渗流模型[2]以及具有起始水力坡降的渗流模型[3]。众多学者基于这3 种非达西渗流模型对土体固结理论进行了研究[4-11]。SCHMIDT 等[11]将指数渗流引入土体一维固结理论，并获得时间因数较小时的解析解答。李传勋等[12-15]基于指数渗流，进一步考虑变荷载、土体非线性、地基成层性等因素，对土体一维固结特性进行了研究。纠永志等[16-17]在对非达西渗流固结的研究中考虑了土体自重的影响，但以上基于指数渗流固结理论的研究并未考虑土体自重的影响。此外，以上基于非达西渗流的固结理论仅限于对荷载形式和土体特性等方面的研究，而综合考虑边界条件的研究较少，但边界条件是求解固结方程不可缺少的条件，对土体固结特性有很大影响，因此，有必要结合边界条件进行研究。

固结理论中运用最广的是Terzaghi 排水边界，其形式简单，便于固结方程求解，但不能反映土体排水边界处孔压随时间的消散情况。基于此，梅国雄等[18-19]提出一种能够反映孔压在排水边界随时间变化的连续排水边界，并获得了该边界条件下瞬时加载的土体一维固结问题解析解。WU等[20-21]基于连续排水边界，研究了双层地基及成层地基一维固结特性。李勇义等[22]根据“孔压叠加”原理，得到任意荷载作用下的连续排水边界表达式，并获得连续排水边界下梯形循环荷载的一维固结解析解。FENG等[23]推导出连续排水边界下考虑土体自重的一维固结解析解。江文豪等[24]基于连续排水边界获得饱和土一维大变形固结解析解。然而，以上连续排水边界的研究均未考虑非达西渗流的影响，而一些渗透性较低的致密黏土中往往存在非达西渗流的现象。

本文作者基于变荷载下的连续排水边界条件，对考虑指数渗流、土体自重及变荷载的饱和土体一维固结问题进行研究。利用有限差分法得到连续排水边界下考虑指数渗流、土体自重及变荷载的饱和土体一维固结问题的解答。最后，讨论不同参数取值对土体固结特性的影响及连续排水边界下达西渗流的适用范围。

1 基本问题

采用的地基固结模型简图如图1所示，其中：H为土层厚度，z表示土体竖直方向，q（t）为施加在土体上的变荷载。荷载形式如图2所示，其表达式为

图1 地基固结模型Fig.1 Foundation consolidation model

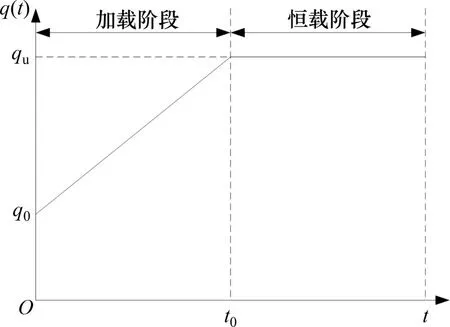
图2 荷载-时间关系Fig.2 Relation between loading and time

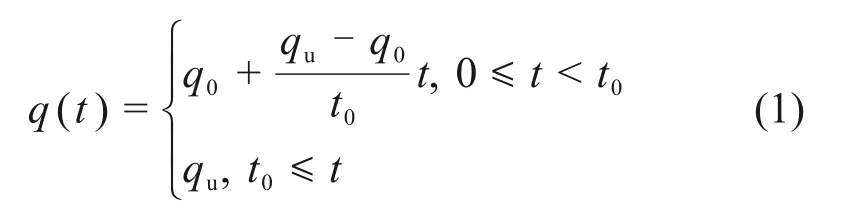
式中：q0为初始荷载；qu为恒载阶段荷载，也是最终荷载；t0为加载阶段完成时刻；t为时间。

假定土中的渗流服从SLEPICKA[2]提出的指数渗流，表达式如下：

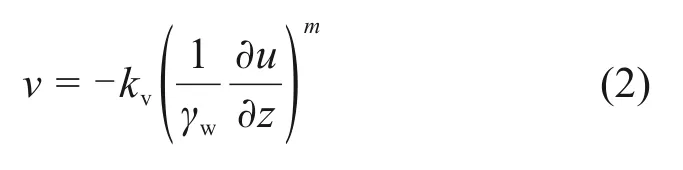
式中：v为渗透流速；kv为渗透系数；u为超静孔隙水压力；γw为水的重度；m为指数渗流定律的指数。

由渗流连续条件可得考虑指数渗流的土体一维固结方程[13]：

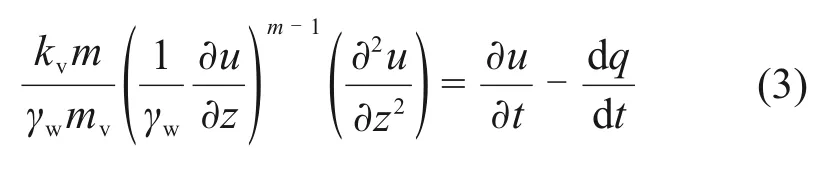
式中：mv为土体压缩系数。

考虑土体自重对固结的影响，自重应力分布形式如图1所示，沿土层深度呈线性分布，则固结方程式（3）求解的初始条件为

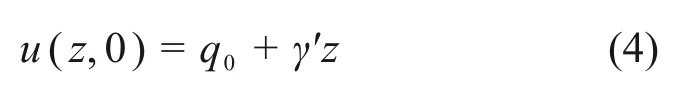
式中：γ′为土体有效重度。

土层顶面采用连续排水边界，该边界形式由梅国雄等[18]提出，适用于瞬时荷载情况。对于变荷载，李勇义等[22]进一步将连续排水边界完善为如下形式：

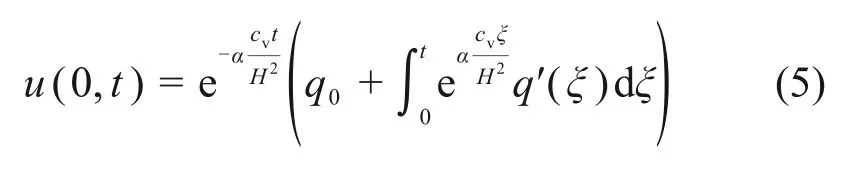
式中：α为反映土体顶面排水性状的界面参数，该值与界面透水性能有关，α越小，则界面透水能力越弱，α越大，则土层顶面排水性能越强，当α增大到一定程度时，连续排水边界可退化为完全排水边界[23]；cv为土的固结系数，cv=kv/（γwmv）。

土层底面采用不透水边界，表达式如下：

2 方程的差分求解及固结度的计算

2.1 差分方程的建立与求解

为便于固结方程的求解及对土体固结特性的分析，定义如下量纲一的参数：

将量纲一的参数代入固结方程及求解条件，则相应的固结方程和求解条件变为

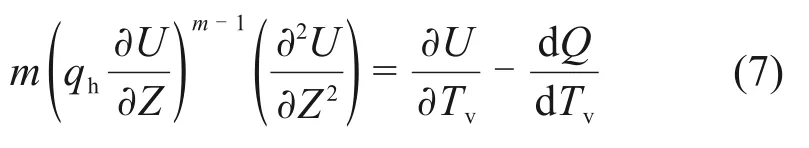
初始条件为

边界条件为：

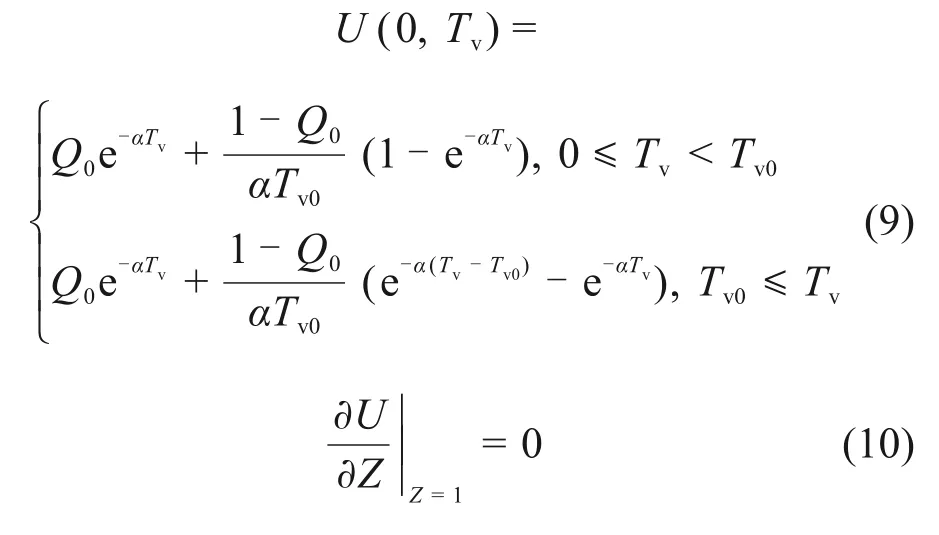
量纲一的固结方程式（7）除m=1 的情况外尚无解析解，因此采用有限差分法进行求解。由于Crank-Nicolson 差分格式具有很好的稳定性[13]，因此本文采用Crank-Nicolson差分格式对量纲一的固结方程式（7）建立差分方程。

对土层进行空间和时间离散，i和j分别表示空间和时间节点，i=0，1，2，···，n；j=0，1，2，···，N。空间节点0 表示土层的表面，时间节点0表示初始时刻。时间步长τ，空间步长h。运用Crank-Nicolson 差分格式对方程式（7）建立差分方程，可得如下差分方程：

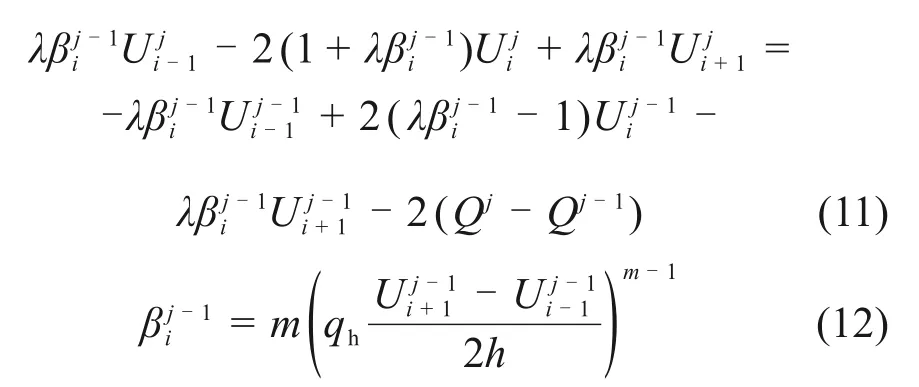
其中：λ=τ/h2；U ij表示j时刻第i节点量纲一的超静孔隙水压力。

相应的求解条件可表示为：

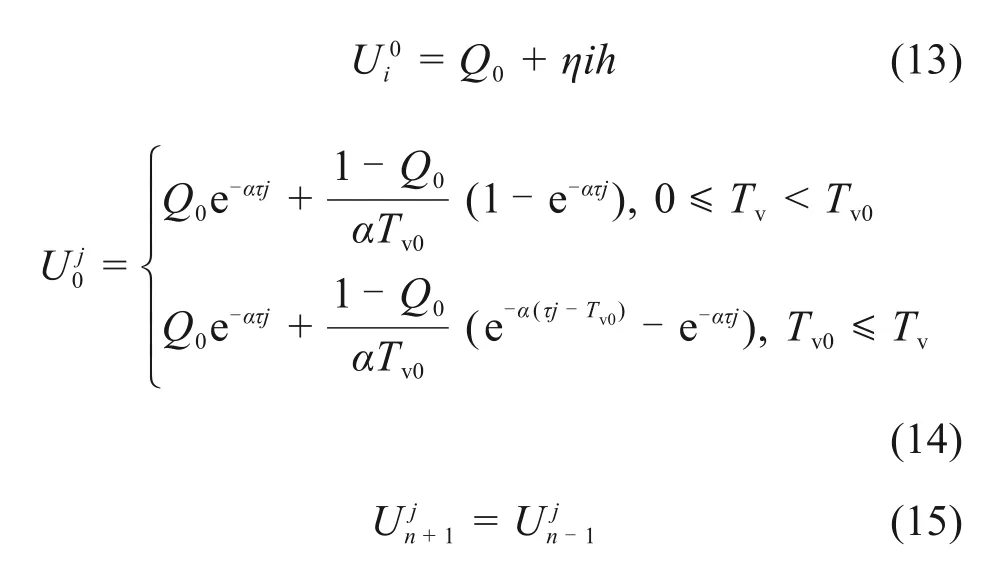
单面排水情况下土体底面渗流速度始终为0，此时，渗流可以按达西定律进行计算。对于单面排水情况，结合求解条件，可将差分方程式（11）表示为如下矩阵形式：

式中：

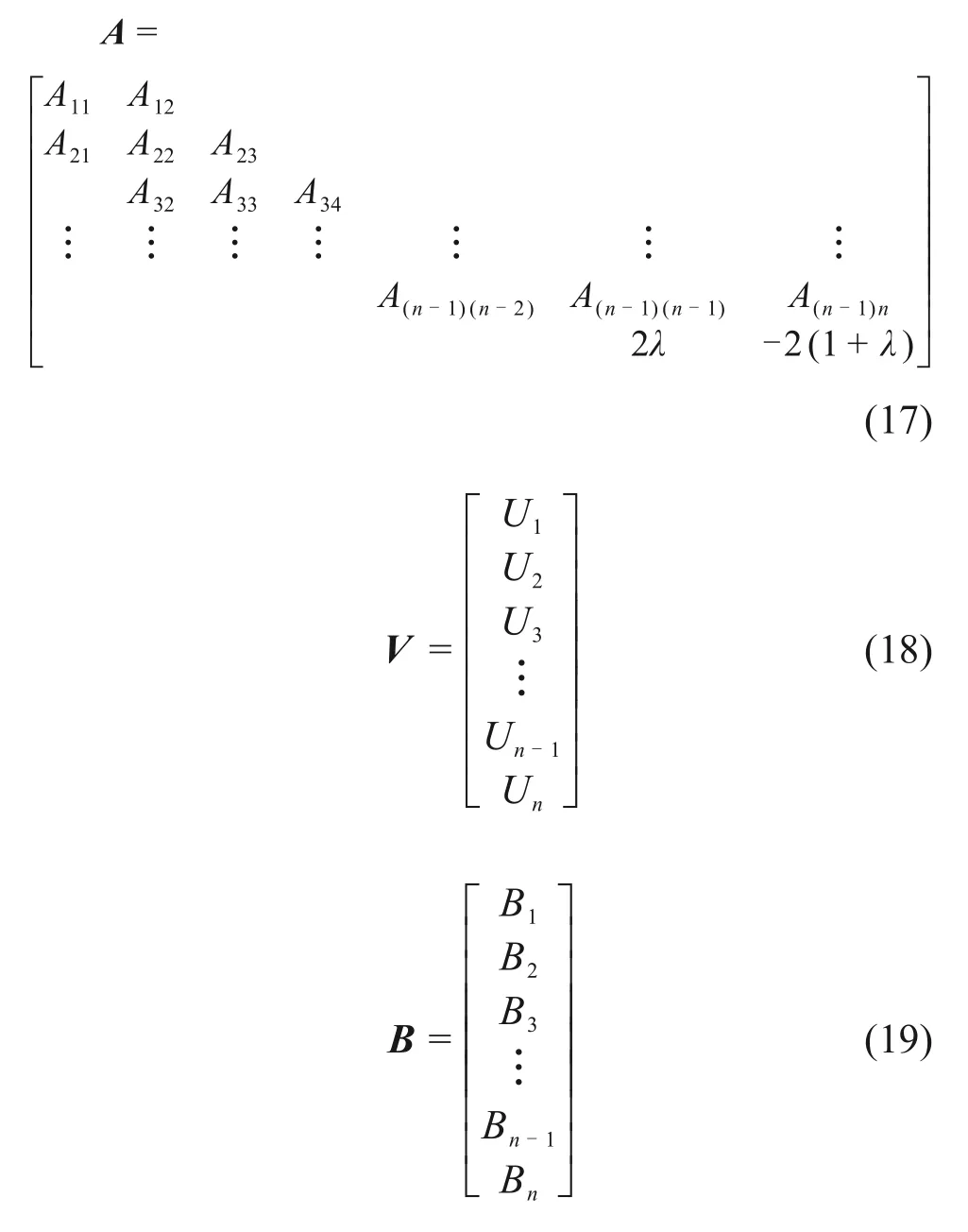
矩阵中j=1，2，···，N。系数表达式如下：

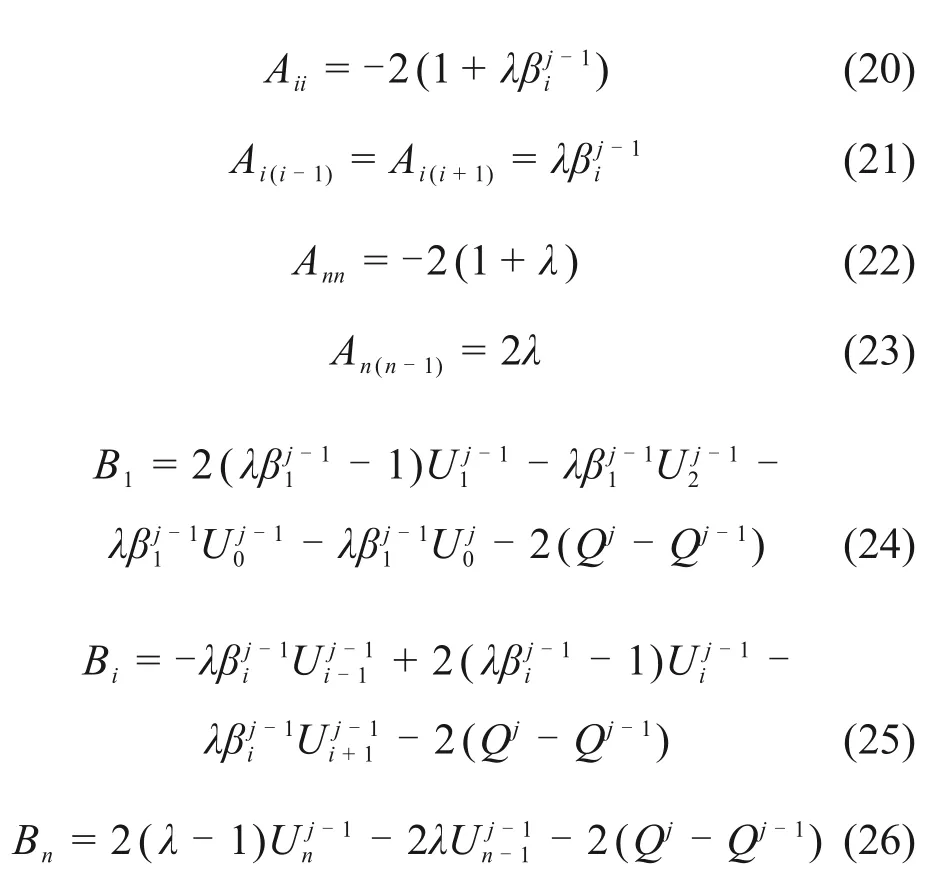
2.2 固结度求解

按沉降定义的平均固结度Us可表示为

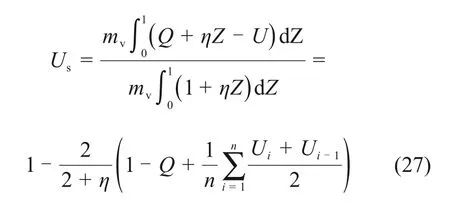
式中：Ui为所求固结度对应时刻土层i节点量纲一的超静孔隙水压力。

3 解答的验证

李传勋等[13]基于Terzaghi单面排水条件，分析了m对土体固结度的影响。图3所示为连续排水边界退化后Us曲线。从图3可以看出：当界面参数α取值很大时，所得解答与李传勋等[13]所得解答一致，说明当α取值很大时，连续排水边界可以退化为Terzaghi排水边界，验证了程序的正确性。从图3还可以看出：在固结初期，土体固结速率随m增大而增大；而在固结后期，土体固结速率随m增大而减小。这是由于在固结初期，土体中水力坡降大于1，当m取值变大时，渗流速度也变快，从而土体固结速率变快；而在固结后期，土体中水力坡降小于1，此时，m取值变大，则渗流速度将变慢，从而土体固结速率变慢。

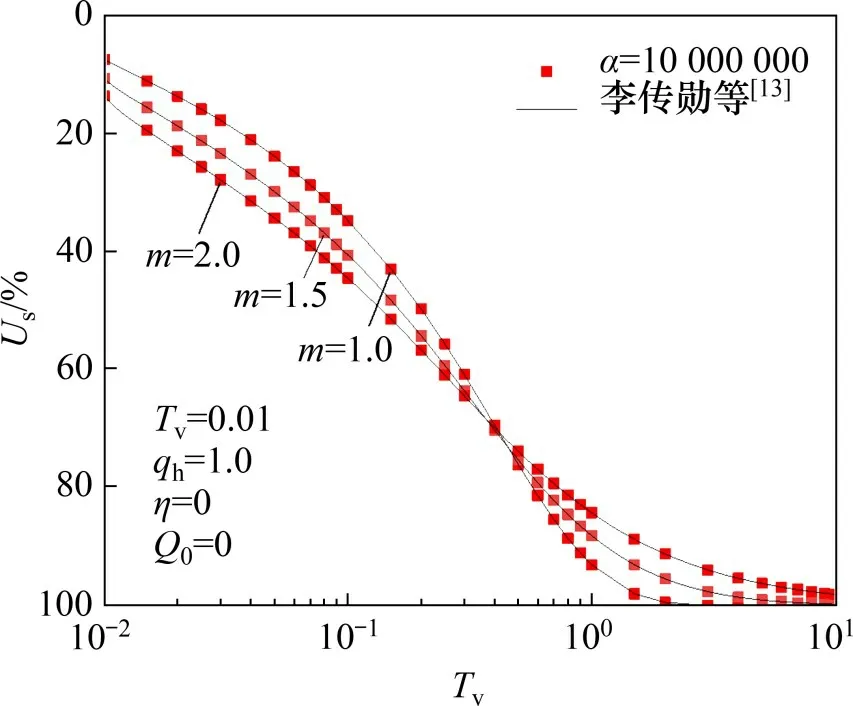
图3 连续排水边界退化后Us曲线Fig.3 Us curve after continuous drainage boundary degradation

4 解答的分析

4.1 不同参数对固结度的影响

图4所示为界面参数α对固结度曲线的影响。界面参数α反映界面排水能力，当α取值变大时，界面排水能力变强，孔隙水排出变快，因此，表现出同一时刻固结度随α增大而变大。从图4可见：当α取值较小时，增大α，土体固结度得到很大提高，随着α增大，固结度增大幅度逐渐减小，固结度曲线逐渐靠近基于Terzaghi排水边界所得固结度曲线；当α=1 000时，基于连续排水边界所得孔压曲线与基于Terzaghi排水边界所得固结度曲线重合，说明当α较大时，连续排水边界能够退化为Terzaghi排水边界，而不需要理论上趋于无穷大才能退化。此外，连续排水边界下土体达到完全固结所需时间与Terzaghi 边界解答结果一致，因此，设计固结排水边界时，按连续排水边界设计不会延长土体固结时间。

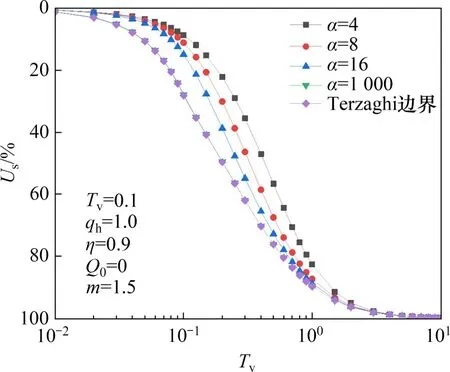
图4 α对Us曲线的影响Fig.4 Influence of α on Us curve

在固定其他参数不变的情况下，Tv0对土体固结速率的影响如图5所示。Q0不变时，Tv0越大则加载速率越慢，反之加载速率越快。从图5可以看出：土体固结度随Tv0增大而减小，说明加载速率越小，则土体固结速率越小；此外，随着Tv0增大，连续排水边界所得固结度解答与李传勋等[13]所得固结度解答差异逐渐减小。这是由于加载速率较小时，土体内超静孔隙水压力增长缓慢，连续排水边界有足够的孔压消散能力。这也说明当外荷载增加缓慢时，工程中固结排水边界按连续排水边界设计不仅可以节省材料，而且其排水能力能达到按完全排水设计的水平。

图5 Tv0对Us曲线的影响Fig.5 Influence of Tv0 on Us curve

图6所示为Q0对土体固结度的影响，Q0由初始荷载与最终荷载之比决定，因此，在最终荷载不变的情况下，初始荷载越大，则Q0越大。从图6可以看出：土体固结度随Q0增大而增大，表明初始荷载越大，土体固结速率越快，此外，Q0主要对土体固结前期的固结速率有影响，在固结后期，不同Q0下的土体固结度曲线趋于重合，即Q0对土体固结后期的固结速率影响很小。

图6 Q0对Us曲线的影响Fig.6 Influence of Q0 on Us curve

在控制其他参数不变的情况下，η对土体固结度的影响如图7所示。η为土体自重与最终荷载之比的自重系数，η越大，则土体自重在固结过程中起到的作用越大。从图7可知：土体固结度随η增大而增大，说明土体自重能够加快土体固结速率，而不考虑土体自重影响的固结速率会偏慢。此外，从图7还可以看出：在不同η下，土体固结初期的固结度曲线差异较大，而固结后期的固结度曲线差异较小，说明土体自重主要对土体固结初期影响较大。

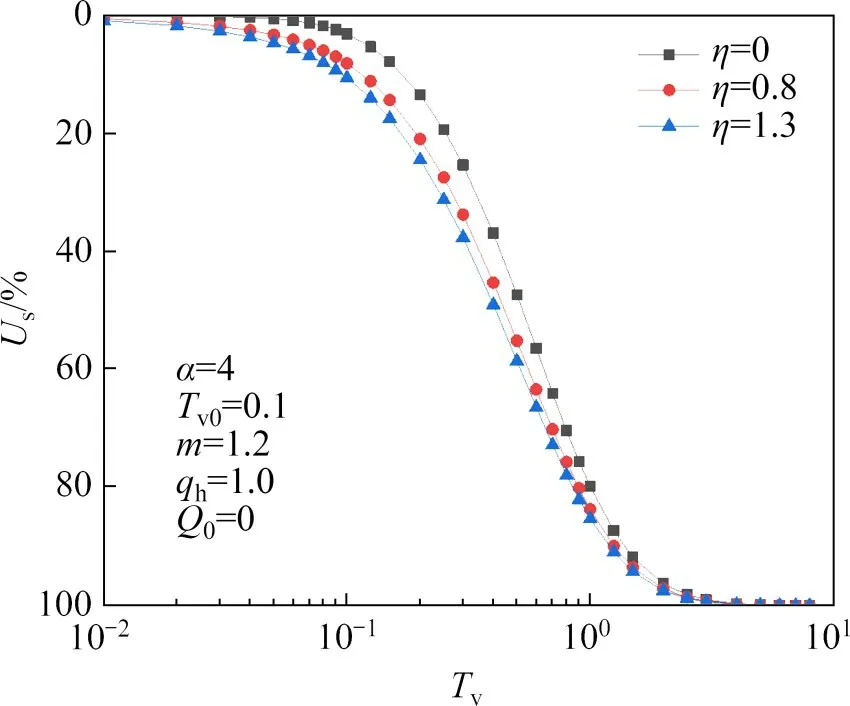
图7 η对Us曲线的影响Fig.7 Influence of η on Us curve

图8所示为不同渗流指数m下qh对土体固结度的影响，qh由荷载等效水头与土层厚度之比决定。从图8可以看出：固结度随qh增大而增大，即qh越大，则土体固结速率越快，说明当施加的外荷载较大或者土层厚度较小时，土体固结速率更快。在固结初期，不同qh得到的固结度曲线差异很小，而在固结中后期，不同qh得到的固结度曲线差异较大，说明qh对土体固结初期的影响较小，而对固结中后期影响较大。从图8（a）和图8（b）还可以看出：在Tv较小时，基于达西渗流的解析解答与qh等于1.0的差分解答差非常小，而随着时间因数的进一步增大，指数渗流解答逐渐偏离达西渗流解答。指数渗流下土体完全固结所需时间始终大于达西渗流下土体完全固结所需时间。在固结初期，qh取值较大，则指数渗流下土体固结速率比达西渗流下土体固结速率快，这说明在固结初期，若施加的外荷载较大或者土层厚度较小，则按达西渗流计算的土体固结速率会偏慢，而若施加的外荷载较小或者土层厚度较大时，则按达西渗流计算的土体固结速率会偏快。但在固结后期，按达西渗流计算的土体固结速率始终大于指数渗流下的土体固结速率。对比图8（a）和图8（b）还可发现，当m较小时，不同qh下所得固结度曲线差距较小，说明m较小时，qh对固结度的影响也较小。

图8 qh对Us曲线的影响Fig.8 Influence of qh on Us curve

若土体有效重度不变，则自重系数η与参数qh成反比。图9所示为自重系数和等效水头共同作用下土体固结度变化规律。由图7可知土体固结度随自重系数η增大而增大，并且η主要影响土体固结前期的固结速率。而由图8可知土体固结度随qh增大而增大，并且qh主要影响土体固结中后期的固结速率。从图9可知：在固结前期，土体固结度随η增大而增大，随qh增大而减小，说明在固结前期η比qh对土体固结速率的影响大；在固结中后期，土体固结度随η增大而减小，随qh增大而增大，说明在固结中后期，qh比η对土体固结速率的影响大。

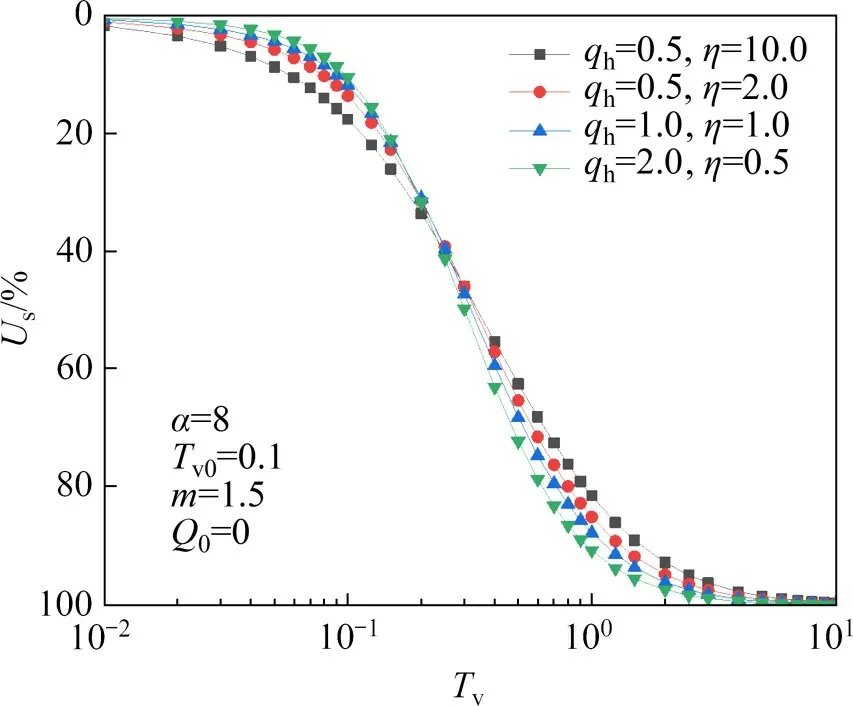
图9 η和qh对Us曲线的影响Fig.9 Influence of η and qh on Us curve

4.2 指数渗流与达西渗流固结度差异

与达西渗流下的土体固结相比，考虑指数渗流的固结求解难度更大，解答形式也更为复杂。若能直接用达西渗流计算，则工程中便于运用。以下对考虑指数渗流的固结度解答与考虑达西渗流的固结度解答的差异进行对比，研究在哪些情况下可以不考虑指数渗流。在以下2种渗流所得固结度差异的分析中，采用瞬时荷载且不考虑土体自重的影响。

由图8可知：当qh取值等于1 时，基于指数渗流所得固结度与基于达西渗流所得固结度差最小，因此，固定qh等于1，分析m对指数渗流与达西渗流所得固结度差的影响，结果如图10所示。图10中，Terzaghi 单面排水边界曲线为Terzaghi 单面排水边界下考虑指数渗流固结度解答与考虑达西渗流固结度解答的差值曲线。从图10可以看出：对于连续排水边界，2种渗流最大固结度差出现在Tv取值等于1.5 时，而Terzaghi 边界下2 种渗流最大固结度差出现在Tv取值等于0.05 时。在Tv取值等于1.5 时，连续排水边界下2 种渗流最大固结度差随α取值增大而变小；当α取值很大时，连续排水边界将退化为Terzaghi排水边界，因此，随着α取值增大，在连续排水边界下，2种渗流固结度差值曲线将逐渐向基于Terzaghi排水边界所得2 种渗流固结度差值曲线靠近，即随着α取值增大，出现最大固结度差时的Tv逐渐向0.05 靠近。由图10还可以看出：在整个固结过程中，当时间因数较小时，连续排水边界下2种渗流所得固结度差非常小，而Terzaghi 排水边界解答下2 种渗流所得固结度差较大；当时间因数较大时，在连续排水边界下，2种渗流所得固结度差略大于Terzaghi排水边界解答下2 种渗流所得固结度差。因此，相对于Terzaghi 排水边界解答，连续排水边界下指数渗流与达西渗流的总体固结度差较小。此外，从图10还可以看出：指数渗流与达西渗流的固结度差随m增大而增大，这是由于m取值越大，指数渗流越偏离达西渗流。

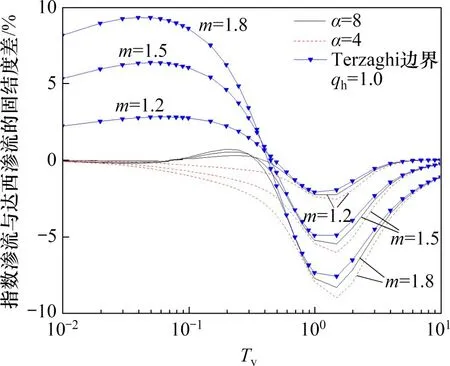
图10 m对指数渗流与达西渗流固结度差的影响Fig.10 Influence of m on difference of consolidation degree between exponential flow and Darcy flow

由图10可知：指数渗流与达西渗流所得最大固结度差出现在时间因数Tv=0.05 和Tv=1.50 这两处。固定参数qh=1.0，Tv=0.05和Tv=1.50，2种渗流固结度差与渗流指数m及界面参数α取值的关系分别如表1和表2所示。由表1可以看出：当Tv等于1.50 时，2 种渗流下固结度差随α增大而减小。从表1可知：要使2 种渗流最大固结度差小于5%，则当α=2 时，需要m≤1.3；而当α≥4 时，需要m≤1.4。由表2可以看出：当Tv等于0.05时，2种渗流下固结度差随α增大而增大，并且随着α增大，固结度差逐渐靠近Terzaghi排水边界解答下的固结度差。对于连续排水边界的解答，最大固结度差与界面参数取值有关，当α≤2 或α≥1 000 时，需要m≤1.3 才能满足2 种渗流的最大固结度差小于5%。而当4≤α≤100 时，只需要m≤1.4 就能满足2 种渗流的最大固结度差小于5%。而对于Terzaghi 排水边界解答，只有当m≤1.3时才能满足2种渗流所得固结度最大差值小于5%的要求。这说明连续排水边界下达西定律的适用性与土层界面排水性能有关，与Terzaghi排水边界相比，连续排水边界下达西定律的适用性更广。

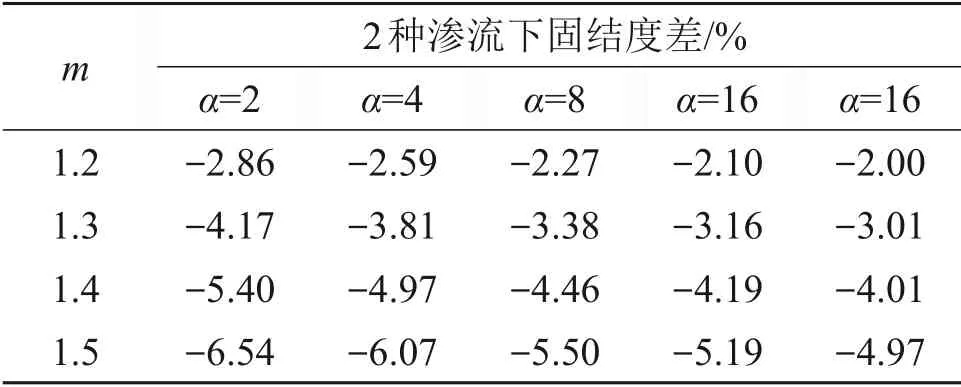
表1 Tv=1.50时指数渗流与达西渗流固结度差Table 1 Difference of consolidation degree between exponential flow and Darcy flow when Tv=1.50

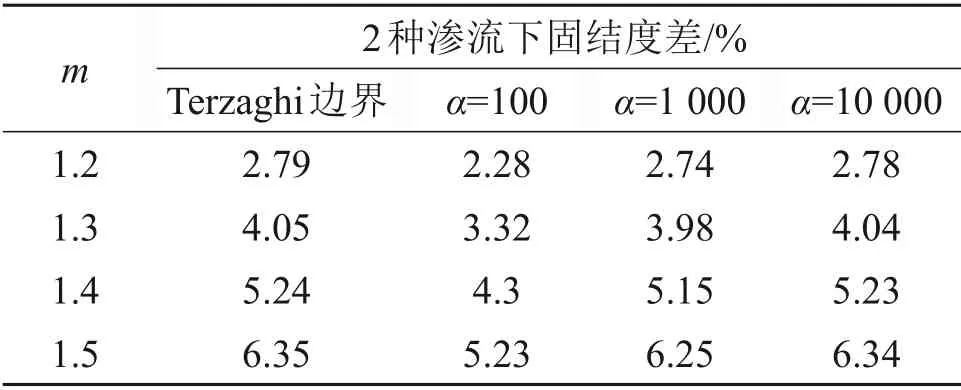
表2 Tv=0.05时指数渗流与达西渗流固结度差Table 2 Difference of consolidation degree between exponential flow and Darcy flow when Tv=0.05

图11所示为当固定m=1.4时，qh对指数渗流与达西渗流所得固结度差的影响。从图11可以看出：当时间因数Tv较小时，Terzaghi排水边界下指数渗流与达西渗流所得固结度差明显大于连续排水边界下2种渗流固结度差；而当Tv取值较大时，连续排水边界下2 种渗流所得固结度差略大于Terzaghi排水边界解答下2 种渗流固结度差；当qh较大时，2种渗流所得最大固结度差出现在固结前期；而当qh较小时，2种渗流所得最大固结度差出现在固结中后期。

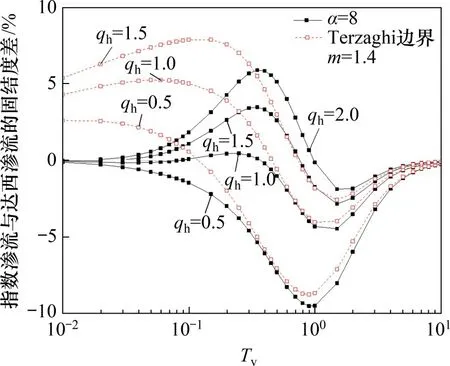
图11 qh对指数渗流与达西渗流固结度差的影响Fig.11 Influence of qh on difference of consolidation degree between exponential flow and Darcy flow

5 结论

1）界面参数α反映界面排水能力，α越大，土体固结越快；连续排水边界解答与李传勋解答差异主要在固结前期，随着Tv变大，两者差别逐渐减小，且两者达到完全固结的时间相等。

2）外荷载增加缓慢时，连续排水边界解答与李传勋解答差异很小，此时，工程中按连续排水边界设计固结排水边界不仅可以节省材料，其排水能力也能达到按完全排水设计的效果。

3）自重系数η和荷载等效水头与土层厚度比值qh越大，土体固结越快。当土体有效重度不变时，η与qh存在反比关系。在η和qh共同作用下，η主要影响固结前期，而qh主要影响固结中后期。

4）当时间因数较小时，连续排水边界下指数渗流与达西渗流所得固结度差非常小，而Terzaghi排水边界下指数渗流与达西渗流所得固结度差较大；当时间因数较大时，连续排水边界下指数渗流与达西渗流所得固结度差略大于Terzaghi排水边界下指数渗流与达西渗流所得固结度差，说明连续排水边界下达西渗流适用的范围更广。

5）不考虑土体自重和变荷载的影响，当qh=1.0时，指数渗流与达西渗流的固结度差最小；m越大，则指数渗流与达西渗流的固结度差越大；当qh=1.0，m≤1.4 且4≤α≤100 时，指数渗流与达西渗流的固结度差小于5%。