一道高中数学毕业会考数列解答题的多种解法与教学建议
2020-07-21夏顺友王常春陈治友汪少祖李艳琴
夏顺友,王常春,陈治友,汪少祖,李艳琴
(1.贵州师范学院 数学与大数据学院,贵州 贵阳 550018;2. 遵义师范学院 数学学院,贵州 遵义 563006;3.贵阳学院 数学与信息科学学院,贵州 贵阳 550005)
数列作为特殊函数是高中数学学习的重要必修内容之一,不仅因为其基本知识本身的重要性,还在于其相关的特殊数学思想方法是继续学习高等数学的基础。但是,因为该部分内容容易和其它部分内容进行综合命题,如与方程(一元一次方程和一元二次方程等)与函数(如二次函数、三角函数等)知识和思想方法(如判别式法、导数法等)、解析几何(如一次和二次曲线等)和不等式知识和思想方法等相结合,从而增加解题的综合性难度,因此,其成为学生考试中要面对的难题之一。[1]
高中数列所包含的基本知识涵盖数列总论、等差数列和等比数列三大块。数列总论包括数列概念、通项公式和前项和公式,以及通项公式和前项和公式的关系,还有特殊数列相关概念(特别是递推数列的特征性质等)。余下两块内容,等差数列和等比数列其实是特殊的递推数列。所以不难把握数列内容的重点和难点应该是通项公式和前项和公式的意义和关系,以及特殊递推数列(主要是等差数列和等比数列);核心思想方法主要是递推归纳、函数和数形结合思想等。[2]
简述数列的核心知识,然后给出2019年7月贵州省高中数学毕业会考数学第43题(数列综合题)的多种解法,接下来提出关于数列教学的几点建议。
1 数列的核心知识
(1)数列总论的核心知识
数列、数列的项、项数、通项公式(an=f(n))、
前n项和公式(Sn=g(n))(其中n=1,2,3,…)的概念以及通项公式和前n项和公式的关系:
递推数列:①am=t1,am+1=t2,…,am+p=tp,②an=f(am,am+1,…,am+p),其中tm,…tm+p,为p个已知常数. 特殊地,①a1=a,②an=f(a1),其中a为已知常数。
注:通项公式和前项和公式的关系是数列的重要内容之一。递推包含的意义是已知数列中任意相邻的p项(条件①),向前或者向后可以依次递推出与数列已知项相邻的其它任意项(条件②)。但是由递推公式给出的数列,要计算p个已知项之外的离第m,m+1,…m+p项很远的项时需要递推很多步,因此,通过递推公式导出通项公式是另一个非常重要的内容。
(2)等差数列的核心知识
等差数列的定义 如果一个数列{an}满足: ①am=a,②当n>m时,an=an-1+d;当n 注:特殊地,①a1=a,②an+=an+d,其中n=1,2,…,而a,d为已知常数. 则称数列{an}是一个公差为d的等差数列. 此时就是各种数学教材上关于等差数列描述性定义的数学化表述。 根据递推、递归或数学归纳法等容易导出等差数列的通项公式:an=am+(n-m)d(为关于变量an,am,n,m,d的一个五元方程),特殊地,an=a1+(n-1)d(为关于an,a1,n,d的一个四元方程)。 注:等差数列的通项公式的变形表达如下:an=dn+(am-md),当d≠0时为n的一次函数;an=(1,n-m)(am,d),其中表示向量的数量积;特殊地,an=dn+(a1-d),当d≠0时为n的一次函数;an=(1,n-1)(a1,d),其中表示向量的数量积。 (1)an=kn+b且b=S1-d=a1-d; (2)Sn=an2+tn 也可以说一个数列是等差数列当且仅当其通项公式和前项和公式分别是一次函数和缺常数项的二次函数或退化形式(即k=0,a=0). 进而有 (1)b=S1-d=a1-d,d=k; 这些公式不仅要从方程与函数的知识和思想方法角度去领会,还要从数形结合思想方法上与向量和解析几何等角度去理解。 注:关于等差数列其它相关延拓性质和思想方法在此略去。等比数列相关知识和思想方法类比可得,在此也略去。 2019年贵州省高中数学毕业会考第43题是关于数列知识,并综合不等式、解析几何和凸集上多元线性函数最值的题目。其题目如下: 43.已知数列{an}的前n项和Sn=pn2+qn,其中p,q为常数. (1) 若S3=15,S5=45,求通项公式an;(5分) (2)若数列{an}满足a12+a32≤10,记z=a3+a4+a5,求z的最大值.(5分)本题满分为10分,(1)与(2)分别为5分和5分. 总试卷328193份,根据评卷系统的最后统计结果,本题平均得分在包含零分卷时是2.54,如果不包含零分卷时,则平均得分是3.62. 具体说来,得分为8分至10分的考生比例是0.4%,而得分为4分至7分的考生比例是38.18%,得分为0.5分至3分的考生比例是34.48%,得分为0分的考生比例是26.94%. 这说明对基础知识、基本技能和基本方法掌握得并不满意,能拿到本题的较高分数的只是少数考生。大多数考生虽然能够掌握好数列、等差数列的基本知识,从而能答对问题的(1)部分,但还不能灵活地综合运用数列和最值求解的相关知识和方法解答所遇到的问题(2),所以这部分考生在问题的(2)部分的失分很多。还有相当多的考生基本知识掌握得不牢固和准确,有的甚至连等差数列通项公式和前项求和公式都不清楚,所以本题的平均得分在4分以下。 该题在考核数列与等差数列的核心知识和方法之外,综合考核了凸集约束条件下多元函数的最值问题,涉及了学生的综合能力,是此次考试中难度最大的题目。 下面先给出该题问题(1)的多种解法。其中法一是命题者给出的参考解答。 当n≥2时,Sn-1=2(n-1)-(n-1)所以an=Sn-Sn-1=4n-3(n≥2).当n=1时,a1=S1=1也满足上式. 所以数列{an}的通项公式为an=4n-3. 故数列{an}的通项公式an=a1+(n-1)d =4n-3. 法三:因为Sn=pn2+qn,所以数列{an}是等差数列。 法四:因为Sn=pn2+qn,所以数列{an}是等差数列。 从而d=a3-a2=4.所以数列{an}的通项公式an=a2+(n-2)d=4n-3. 即a1+a5=18 ① 即3a1+a5=20 ② 故数列{an}的通项公式an=a1+(n-1)d =4n-3. 法六:因为Sn=pn2+qn,所以数列{an}是等差数列。 由S5=a1+a2+a3+a4+a545,S3=a1+ a2+a3=15,及an=a1+(n-1)d可得 S5=5a1+10d=45 ① S3=3a1+3d=15 ② 由①②解得a1=1,从而d=4. 所以数列{an}的通项公式an=a1+(n-1)d=4n-3. 下面再给出该题问题(2)的多种解法. 其中法一是命题者给出的参考解答。 法一:由Sn=pn2+qn可得a1=p+q,a3 =S3-S2 =5p+q,z=a3+a4+a5=S5-S2=21p+3q. 设a1=p+q=x,a3=5p+q=y, 又因a12+a32≤10,所以x2+y2≤10. 所以当且仅当p=1,q=-2时,z取得最大值15. 法二:由Sn=pn2+qn可得a1=p+q,a3 =S3-S2=5p+q,z=a3+a4+a5=S5-S2 =21p+3q. 所以要使得二元线性目标函数值z最大,必须有点(a1,a3)在由a12+a32≤10表示的圆形区域的边界上,即直线l:3a1-9a3+2z=0与圆a12+a32=10相切,可求得(a1,a3)=(-1,3). 法三:由Sn=pn2+qn可得a1=p+q,a3 =S3-S2=5p+q,z=a3+a4+a5=S5-S2 =21p+3q. 由a12+a32≤10,得(p+q)2+(5p+q)2≤10,化简可得13p2+6pq+q2≤5. 则z2=(21p+3q)2 =45(13p2+6pq+q2)-(2p+q)2. 要使得z2最大,必须使得(2p+q)2=0且13p2+6pq+q2=5解得p=1,q=-2,且最大值z=15. 所以当且仅当p=1,q=-2时,z取得最大值15. 法四:因为Sn=pn2+qn,所以数列{an}是等差数列,故z=a3+a4+a5=3a4. 所以z=3a4最大时,必须a4=5,从而z最大=15. 于是(5-3d)2+(5-d)2≤10时,d=2p=2, p=1.从而p=1,q=-2. 所以当且仅当p=1,q=-2时,z取得最大值15. 法五:因为Sn=pn2+qn,所以数列{an}是等差数列。 设公差为d,所以z=a3+a4+a5=3a2+6d. ≤225,解得-15≤z≤15. d=2时,z最大=15,从而p=1,q=-2. 所以当且仅当p=1,q=-2时,z取得最大值15. 注:该解法用到柯西不等式。 法六:由Sn=pn2+qn可得a1=p+q,a3 =S3-S2=5p+q,z=a3+a4+a5 =S5-S2=21p+3q. 所以当且仅当p=1,q=-2时,z取得最大值15. 注:该解法用到柯西不等式。 法七:由Sn=pn2+qn可得a1=p+q, a3=S3-S2 =5p+q,z=a3+a4+a5=S5-S2=21p+3q. 于是z2=(21p+3q)2 z最大=15 . 于是p=1,q=-2时z最大=15. 所以当且仅当p=1,q=-2时,z取得最大值15. 注:该解法用到柯西不等式。 法八:由Sn=pn2+qn 可得a1=p+q,a3=S3-S2 =5p+q,z=a3+a4+a5=S5-S2=21p+3q. 即13p2+6pq+q2≤5. 于是z=21p+3q =3[p+p+p+p+(3p+q)] q=-2时,z最大=15. 所以当且仅当p=1,q=-2时,z取得最大值15. 注:该解法用到柯西不等式。 于是a1=-1,a3=3时z最大=15. 从而p=1,q=-2. 所以当且仅当p=1, q=-2时,z取得最大值15. 注:该解法用到柯西不等式. 法十:由Sn=pn2+qn可得 a1=p+q,a3=S3-S2 =5p+q,z=a3+a4+a5=S5-S2=21p+3q. 即13p2+6pq+q2≤5, 也即0≤(3p+q)2≤5-4p2,从而 p=1,q=-2时z最大=15. 所以当且仅当p=1,q=-2时,z取得最大值15. 注:该解法用到函数导数法解决不等式恒成立的方法。 法十一:因为Sn=pn2+qn,所以数列{an}是等差数列,则可设an=nx+y,于是 z=a3+a4+a5=3a4=3(4x+y), 得x=2时f最小(x)=f(2)=5,即x=2时,z最大=15,此时y=-3. 因此由a1=S1=p+q=x+y,a2=S2-S1=3p+q=2x+y可得p=1,q=-2时z最大=15. 所以当且仅当p=1,q=-2时,z取得最大值15. 注:该解法用到函数导数法解决不等式恒成立的方法。 利用凸规划或可行域法分析出直线与圆相切后,可以用圆心到切线距离等于半径、德尔塔(大于)等于0法、三角函数代换法、正交法,或利用向量法或柯西不等式方法、函数极值法、函数单调性法求切点或临界点等其它微小的变化。还可以利用拉格朗日乘数法等. 在此不再一 一列出。 等差数列作为离散化的特殊一次和二次函数包括其退化情形,需要数形结合的函数与解析几何的知识和思想方法。而递推迭代是一种基本的算法思想,涵盖有限到无限的过程。不论数列的基本知识还是基本思想方法都是初等数学的重要内容,也是后续学习的基础。 (1)在基于学生生活现实和数学现实基础上,要特别重视数学化和再创造的过程教学体验是课堂教学质量的基础。 建议特别注意教学中在初中学习的一次函数和二次函数知识和数形结合方法,以及利用梯形或三角形建构平行四边形面积等数学现实基础上,建构、理解和掌握数列相关知识和方法,强化过程体验学习模式,真正做到基础扎实。 (2)在课程标准要求的基础上,要特别重视“基于教材而不拘泥于教材,源于教材而超出教材”是课堂教学质量基本保障的核心。 建议特别注意教学中不只是停留在学教材和教教材的低级僵化水平上,要在引入、新知学习、综合提高方面不拘泥于教材而高于教材。真正做到内化的心领神会的理解知识方法。 (3)在掌握基础知识和基本思想方法上,要特别重视纵向深度的拓展和横向广度的延拓与融合是课堂教学效果提升的关键。 建议特别注意教学中引导学生认识数学知识与方法的核心是对世界认识的数学化的简化,不论是横向还是纵向拓展知识方法都是在简化人们对世界的某方面本质的简化表述,真正做到对知识方法的融会贯通。
2 2019年7月贵州省高中数学毕业会考第43题的学生答题基本情况和该题的分析及其多种解法



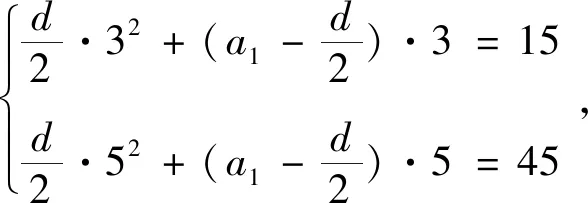


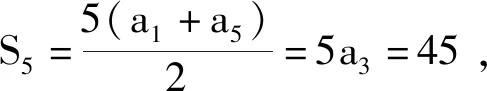
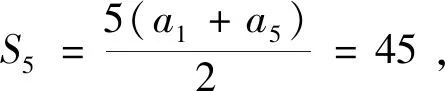
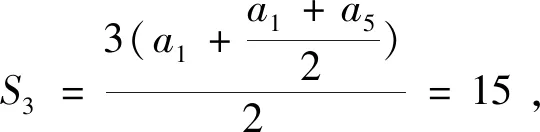
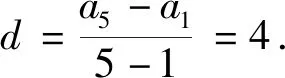

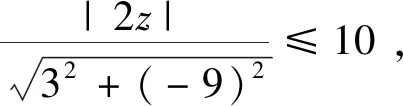
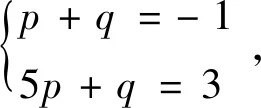
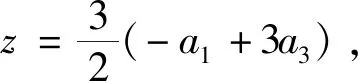
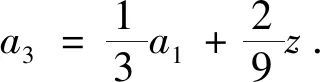
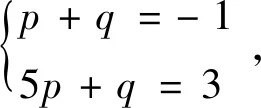



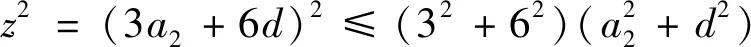


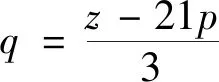
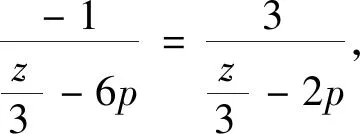

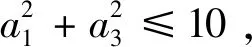

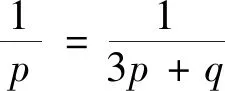









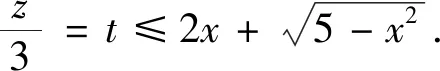
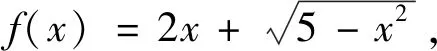
3 关于高中数列教学的一些建议
