基于光纤应变传感器的型架定位器位置检测方法研究
2020-07-21李现坤曾德标楚王伟伍承旭
李现坤,曾德标,楚王伟,伍承旭
(1.成都飞机工业(集团)有限责任公司,四川成都610092;2.四川省航空智能制造装备工程技术研究中心,四川成都610092)
在飞机装配过程中,型架定位器状态的稳定性关系着飞机各个部件的装配精度,是保证飞机装配质量和协调性的重要指标[1-6]。目前,针对定位器位置的检测,主要采用直接测量的方式:首先采用激光跟踪仪对现场基准点进行测量和拟合,然后依次检测各个定位器的位置是否满足要求,如不满足,则通过人工调整的方式使定位器满足定位精度要求。然而,由于型架结构较大,测量视线容易被遮挡,导致个别定位器位置无法被检测到。此外,由于成本所限,只能对定位器进行逐个检测,而无法同时对所有定位器进行检测,这可能造成个别定位器位置偏差过大,从而影响飞机装配质量[7-8]。
为了实现飞机装配过程中型架定位器位置的准确检测,笔者提出了一种基于光纤应变传感器的定位器位置检测方法:利用光纤应变传感器采集型架主体及定位器组件关键特征部位的位置信息,并采用BP神经网络算法对采集的数据进行分析和处理,建立飞机型架不同区域应变量与定位器位置变化量之间的映射关系,实现对飞机装配过程中定位器位置的实时检测[9]。
1 光纤应变传感器
飞机装配现场环境恶劣,传统应变传感器在粘贴、布线等方面难以满足使用要求。光纤应变传感器具有体积小、质量小、精度高等优点[10-13],容易实现对被测信号的远距离检测,同时具有高度的集成性,即在一根光纤上可以串行或并行多个传感器,可同时传输多种信号。光纤应变传感器利用光导纤维的传光特性,将来自光源的光传入调制器。在调制器内,由于应变与光的相互作用,使得纤芯的有效折射率和光栅周期发生变化,进而导致纤芯的中心波长发生变化。通过检测反射或透射中心波长的漂移量,可以得到应变的变化。根据光纤光栅的布拉格方程,得出波长漂移与应变之间的关系:

式中:λB为中心波长;ΔλB为波长的偏移;Kε为光纤灵敏度系数,可以根据光纤的固有属性计算得出;εz为应变大小;为光栅的有效折射率;p11和p12均为石英的弹光系数;u为石英光纤的泊松比。
2 BP神经网络算法
飞机型架结构复杂,其应变量与定位器位置变化量之间的数学关系很难通过简单的计算来获取。因此,将型架应变与定位器位置变化之间的关系看作黑箱问题,基于BP神经网络算法,以大量输入与输出数据作为支撑,获取型架应变与定位器位置变化的传递关系。基于多层前馈网络构建的BP神经网络由输入层、隐藏层和输出层组成,其结构如图1所示。理论上,3层的BP神经网络结构能以任意精度逼近复杂的非线性函数关系[14-18]。

图1 BP神经网络结构Fig.1 Structure of BP neural network
图1中:输入层有m个神经元,其输入矢量x∈ℝm,x=(x1,x2,…,xM)T;隐藏层有j个神经元,其输出矢量v∈ℝj,v=(v1,v2,…,vJ)T;输出层有p个神经元,其输出矢量y∈ℝp,y=(y1,y2,…,yP)T;期望输出矢量d∈ℝp,d=(d1,d2,…,dP)T;输入层到隐藏层的权重为ωmj,阈值为θj;隐藏层到输出层的权重为ωjp,阈值为θp。
BP神经网络算法的计算过程分为2步:一是输入信息的正向传播;二是计算误差的反向传播。在信息的正向传播过程中,输入信号从输入层通过激活函数向隐含层和输出层传播。如果在输出层得不到期望的输出值,即输出值与目标值的误差较大,则将误差信号由输出层向输入层逐层反推,修改各层神经元之间的权重和阈值,以使神经网络朝误差减小的方向变化。当达到期望的预测精度时,计算停止,此时得到的权重、阈值矩阵即为BP神经网络模型的参数。BP神经网络模型中各变量之间的关系如下:
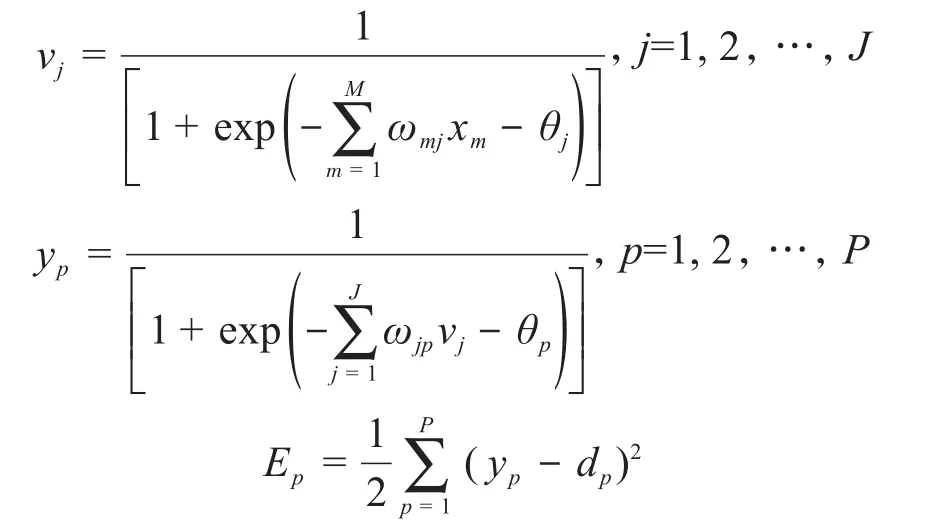
式中:Ep为训练样本的总误差。
3 型架定位器位置检测应用分析
3.1 试验平台
为了验证本文提出方法的有效性,选定某型工艺装备,搭建如图2所示的试验平台,该平台包括型架主体、定位器组件、光纤、应变传感器及多角度加载装置。在实际装配过程中,由于装配工艺流程不同,定位器末端受到的载荷也不同。多角度加载装置可根据装配过程中定位器的实际受载范围,对它施加不同大小和方向的载荷。在试验过程中,通过对定位器组件末端施加不同大小和方向的载荷,使得型架主体及定位器组件产生应变,同时使定位点偏离理论位置。

图2 型架定位器位置检测试验平台Fig.2 Test platform for position detection of jig positioner
3.2 型架定位器位置检测试验
3.2.1 样本数据
输入数据通过多角度加载装置获取。如图3所示,多角度加载装置包括4个加载平面,每个加载平面均可对定位器末端施加0°,±15°,±30°,±45°和±60°方向的载荷。在试验过程中,通过改变加载平面、加载角度和载荷大小来实现定位器末端不同的加载。记录加载时光纤应变传感器采集的应变量和定位点的位置变化量,将它们作为后续神经网络训练及验证的样本数据。
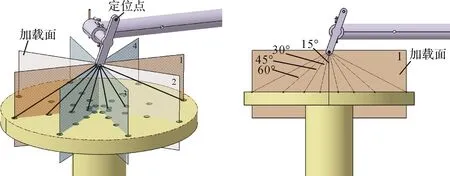
图3 多角度加载装置结构示意图Fig.3 Structure diagram of multi-angle loading device
3.2.2 试验结果与分析
利用MATLAB软件的newff函数创建BP神经网络模型,隐藏层的传输函数选用tansig函数,输出层选用purelin函数。输入层和输出层的神经元个数由输入和输出样本的维度确定,其中:输入层神经元个数为16个,输出层神经元个数为3个,根据试算法确定隐藏层神经元个数为10个,则构建的BP神经网络模型结构为“16-10-3”。
1)偏移角度对模型预测精度的影响。
为了验证加载偏移角度对训练后BP神经网络模型预测精度的影响,在某一加载平面内,选取加载角度为0°时获得的输入和输出数据200组,作为BP神经网络模型的训练样本。选取加载角度为15°,30°,45°,60°时获得的数据(各20组),将其输出数据作为验证样本,以此分析偏移角度对训练后BP神经网络模型预测精度的影响规律。实验结果如图4所示。
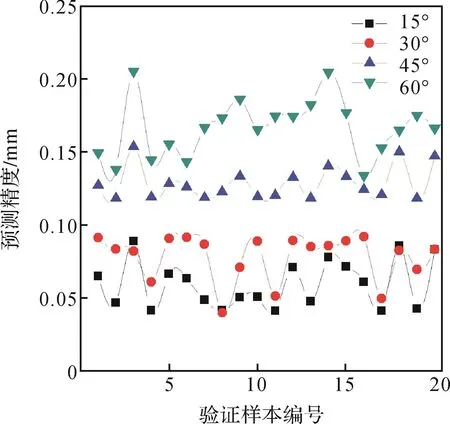
图4 偏移角度对BP神经网络模型预测精度的影响Fig.4 Effect of migration angle on BP neural network model prediction accuracy
由图4可以看出:随着偏移角度的增大,其训练模型的预测精度下降;当偏移角度大于30°时,精度超过0.10 mm,超出定位器的定位精度要求。
2)型架定位器在平面内受载时的试验结果与分析。
根据上述偏移角度对训练后BP神经网络模型预测精度的影响结果,任意选取某一加载平面,分别选取加载角度为0°,±30°和±60°时获得的输入和输出数据各50组,作为该加载平面的BP神经网络模型的训练样本。选取加载角度为±15°和±45°时获得的数据各20组,将其输出数据作为验证样本,检测BP神经网络模型对定位器在平面内受载时位置变化的预测精度。实验结果如图5所示。
由图5可以看出,当训练样本数量一定时,在平面范围内,模型的预测精度与载荷角度无关,仅与偏离角度有关。以30°的间隔选取加载位置,训练后模型的预测精度较高,满足定位精度要求。
3)型架定位器空间受载时的试验结果与分析。
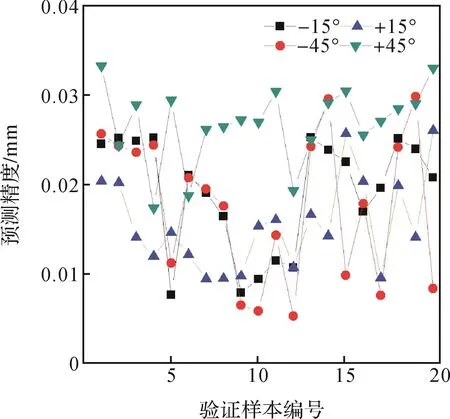
图5 型架定位器在平面内受载时BP神经网络模型的预测精度Fig.5 Prediction accuracy of BP neural network model with jig positioner loaded in a plane
根据上述实验结果,对定位器受载空间进行分割,选取加载平面1和3,在每个加载平面内选取0°,±30°和±60°的加载角度,以空间90°间隔、平面30°间隔选取加载位置,在每个加载位置上获取输入和输出数据100组,作为BP神经网络模型的训练样本。在加载平面2和4中随机获取不同角度的数据各20组,将其输出数据作为验证样本,检测BP神经网络模型对定位器以空间90°间隔受载时位置变化的预测精度。实验结果如图6所示。
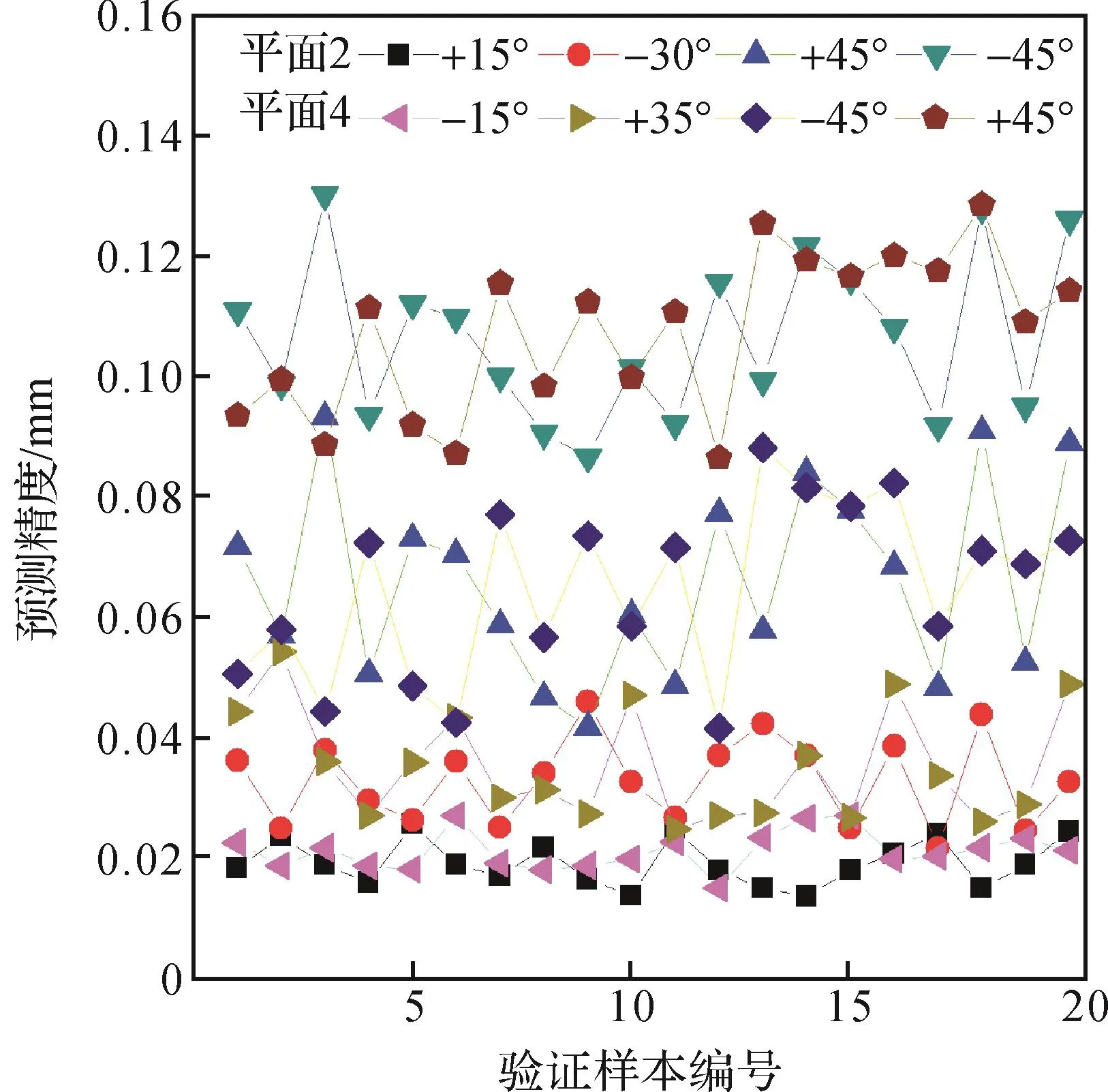
图6 型架定位器以空间90°间隔受载时BP神经网络模型的预测精度Fig.6 Prediction accuracy of BP neural network model with jig positioner loaded at a space interval of 90°
在加载平面1,2,3,4内选取0°,±30°和±60°的加载角度,以空间45°间隔、平面30°间隔选取加载位置,在每个加载位置上获取输入和输出数据50组,作为BP神经网络的训练样本。旋转多角度加载装置,以旋转后获取的输出数据作为验证样本,检测BP神经网络模型对定位器以空间45°间隔受载时位置变化的预测精度。实验结果如图7所示。
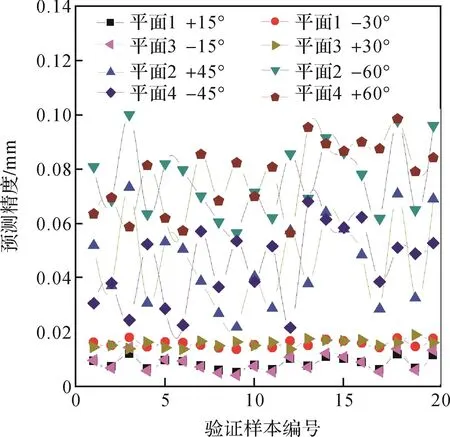
图7 型架定位器以空间45°间隔受载时BP神经网络模型的预测精度Fig.7 Prediction accuracy of BP neural network model with jig positioner loaded at a space interval of 45°
由图6和图7可知:对于空间范围内某一加载平面,随着偏移角度的增大,模型的预测精度降低;随着空间加载间隔的缩小,模型在同一加载角度下的预测精度提高。在一定空间范围内,模型的预测精度与加载位置的间隔有关:加载位置的间隔越小,覆盖率越高,在该空间范围内模型的预测精度越高。
4 结论
本文提出一种基于光纤应变传感器的型架定位器位置检测方法。搭建了型架定位器位置检测试验平台,采用BP神经网络算法对试验数据进行分析和处理,建立型架不同区域的应变与定位器位置变化量之间的数学模型,对装配过程中定位器位置进行实时检测。
1)由试验结果可知,BP神经网络模型对定位器位置变化的预测精度满足定位要求,验证了本文方法的可行性,具有实际应用价值。
2)型架不同区域的应变通过光纤应变传感器获取,投入成本较低,易于推广和应用。
3)与传统的用数字化设备直接测量的方式相比,采用间接的方式检测定位器的位置,弥补了因视线遮挡而造成个别定位器位置无法被检测的缺陷。通过对装配过程中所有定位器位置进行实时检测,解决了定位器位置偏差过大造成的飞机部件检测质量差的问题,提升了飞机的装配质量。
