卷积神经网络在结构损伤检测中的应用

罗雨舟，向天宇，郝柳青

(西华大学 土木建筑与环境学院，四川 成都 610039)

土木工程结构在其使用寿命期间易在外力或介质的侵蚀下造成性能的劣化，从而导致安全性降低和经济损失，因此对结构进行健康检测很有必要。国内外学者在提取结构特征并将其运用于土木工程结构的实时监控方面都做出了巨大贡献，但距实际工程应用尚有距离[1]。对于传统的损伤检测方法，需先构建结构数学模型，随后使用该模型阐明结构行为并建立损坏条件与结构响应之间的相关性[2]。但是，当检测遇到复杂的系统时，传统的损伤检测方法可能存在诸如测量噪声和建模误差等困难，并且该方法无法实现结构的实时损伤检测。在结构动力响应特性方面，尽管通过提取模态特征能够较为准确地判断结构的损伤状态[3,4]，并且能够实现结构的实时检测。但是，不同温度和湿度条件下自振频率的变化[5]以及激励大小和类型的未知对该方法造成了一定的局限。与此同时，也有不少学者利用支持向量机、神经网络等机器学习算法进行损伤特征的提取和分类。但是，机器学习需要海量的训练样本，其需要学习的参数量巨大且容易出现过拟合现象[6]，因此该方法受到了极大限制。

近年来，深度学习在游戏博弈、图像识别以及无人驾驶等领域取得了非常成功的应用[7～9]，引起了不同学术领域对这一科学问题的广泛关注。卷积神经网络(Convolutional Neural Network, CNN)是深度学习中广泛应用的算法之一，其思想源于Hubel和Wiesel[10]对动物视觉皮层细胞研究提出的感受野(Receptive Field)概念。到1998年，Lecun等[11]提出了第一个正式的CNN模型LeNet-5，如图1所示。相比于传统神经网络，卷积神经网络更类似于生物神经网络，采用局部连接和权值共享的网络结构，大大减少了所需训练参数的数量，在一定程度上降低了过拟合的可能。因此，不少学者将CNN应用于结构损伤检测。Cha等[12]利用CNN出色的图像识别能力，以混凝土裂缝图片作为输入，研究了CNN对混凝土结构裂缝等缺陷的图像识别精度。李雪松等[6]通过CNN提取结构加速度信号的特征向量，并且与小波包变化法和经验模态分解法做了系统对比，结果显示CNN自主提取的特征向量能更准确地反映结构的损伤情况。Abdeljaber等[13,14]均采用了一维向量作为输入的卷积神经网络进行了结构损伤诊断的研究。Hoang等[15]指出振动信号中包含了能反映损伤情况的丰富信息，因此将轴承振动信号转化成二维灰度图像，再利用CNN从中学习抽象的高级损伤特征，最后通过Softmax算法实现损伤的诊断。因此，受到上述学者研究成果的启发，本文拟采用结构在不同类型激励作用下的加速度时程信号作为输入，研究CNN在提取损伤特征过程中对激励类型的鲁棒性，并研究了CNN的抗噪能力。

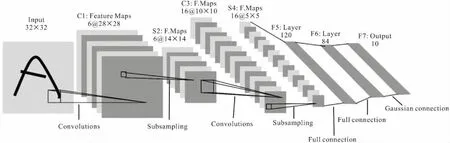
图1 LeNet-5结构

1 卷积神经网络

1.1 卷积神经网络的基本原理

一个完整的网络由输入层、卷积层、池化层、全连接层和输出层组成。以LeNet-5网络为例，它包括一个输入层，两个卷积层，两个池化层，两个全连接层和一个输出层。

CNN的核心理论在于局部感受野。局部感受野的概念来自于生物神经科学，从直观上讲，局部感受野即视觉感受区域。如图2所示，生物神经科学已发现，在视觉认知过程中，通过对局部信息的提取加工得到更高层次的信息特征，即为局部感受野的概念。

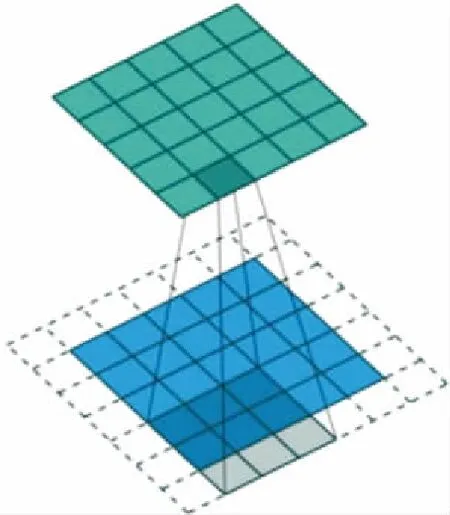
图2 局部感受野示意

1.2 卷积层

在卷积神经网络中，采用卷积层这一数学模型来模拟局部感受野这一神经科学现象。卷积层的输入为上一网络层的输出，如图3所示，通过局部感受野对输入矩阵进行卷积操作，随后经过激活函数的激活形成该层网络的输出。

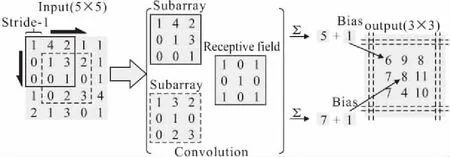
图3 卷积层

非线性激活从生物意义上可以理解为当传递信号的值大于一个特定的阈值时，下个神经元才会被激活，否则抑制。在CNN中，其意义在于感受野提取到的某一个特征的特征强度是否达到一定标准。目前，如式(1)所示ReLU激活函数因其收敛速率快且能达到较高的精度而被广泛应用。

ReLU(x)=max{0,x}

(1)

总的来讲，卷积层数学模型可以定义为：

(2)

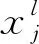
1.3 池化层

经过卷积层对信息的局部感知化后，需要用池化层对信息进行压缩。池化方式一般分为两种，最大值池化和均值池化。最大值池化是提取子矩阵中的最大值作为输出，而均值池化是计算子矩阵的平均值作为池化结果，如图4所示。池化层的主要目的是对卷积层中提取的特征进行汇总并对数据进行压缩，从而使CNN能够抽取的特征范围更广。另外，池化操作使模型更关注是否存在某种特征而非这些特征在哪里，且在一定程度上防止过拟合。

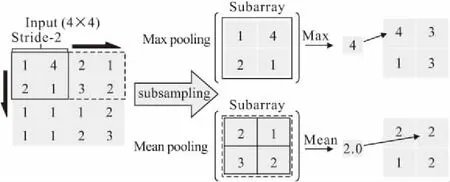
图4 下采样层

1.4 全连接层

在经过多次卷积池化处理后，模型连接着1个及以上的全连接层，如图5所示。

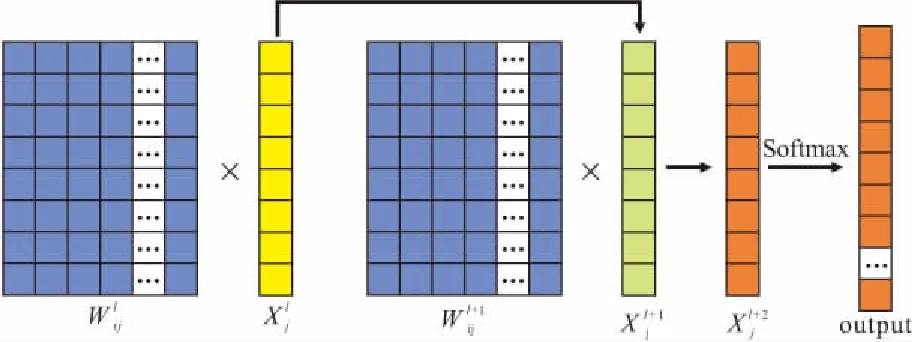
图5 全连接层

与多层感知器类似，全连接层中的每个神经元均与前层神经元连接，其主要功能是整合卷积池化层中具有类别特征的信息。同时，将卷积池化层中所提取到的特征信息映射到样本标记空间中，实现对输入数据的分类，因此全连接层在整个CNN中起到了分类器的作用，其核心操作是如式(3)的线性变化。

y=Wx

(3)

式中：x为该层的输入(即前层的输出)；y为该层的输出；W为权值。

1.5 Softmax层

CNN在经过多个卷积、池化操作和全连接层之后，已经完成了输入信号的特征提取和压缩，通过Softmax层实现对结构损伤的诊断。Softmax是深度学习多分类问题中的核心算法，其实质是一个概率表达式，如式(4)所示。

(4)

式中：i为m个训练集中第i个训练样本；j为n个分类标签中的第j个标签；θ为权重；x(i)为Softmax层的输入。

2 CNN在损伤诊断中的应用

2.1 研究思路及方法流程

根据结构动力学原理可知，结构振动具有一定的规律性，并且主要表现在其振型上。对于损伤结构而言，结构的振型中必然包含了能反应损伤的信息。因此通过提取振型中的损伤特征，就能够实现对结构的损伤诊断。对于结构振型，现阶段不能直接进行采集，但是结构上多质点的振动规律能够反映出结构整体的振型。因此，本文通过采集结构上多质点的加速度信号组成矩阵，就能形成包含二维损伤特征的特征图作为网络的输入层。对于二维特征图提取，CNN的局部感受野具有天生的优势。通过卷积层模型，局部感受野实现对多通道信号特征的提取，这样也就能在一定程度上得到了更广阔的损伤信息。

基于上述分析，本文通过有限元软件，模拟了随机损伤的简单结构，提取结构在不同类型激励作用下的加速度时程信号作为CNN的输入。图6展示了该方法的基本流程，首先通过数值模拟试验提取结构多点加速度信号组成矩阵，随后搭建CNN模型对该加速度矩阵进行特征提取并实现损伤诊断，最后通过预测集对模型进行测试，计算其识别精度。

图6 本文方法流程

2.2 CNN架构

CNN超参数的选择是一项十分繁琐的工作，且目前对于这些参数的优化尚未有明确的指导原则。因此，本文通过反复试验探索结构损伤诊断的最优架构。首先为确定CNN架构超参数，本文进行了大量试验，在保持迭代次数、卷积核尺寸及个数不变的条件下，研究了CNN的最高识别精度，如图7所示。随后控制卷积池化层数不变，研究了卷积核个数的影响。根据图示结果并综合计算时间成本，本文推荐的卷积层数量为2～3个。对于卷积核，尺寸上本文采用3×3，第一卷积层推荐采用3～4个，第二、三卷积层推荐6～8个。

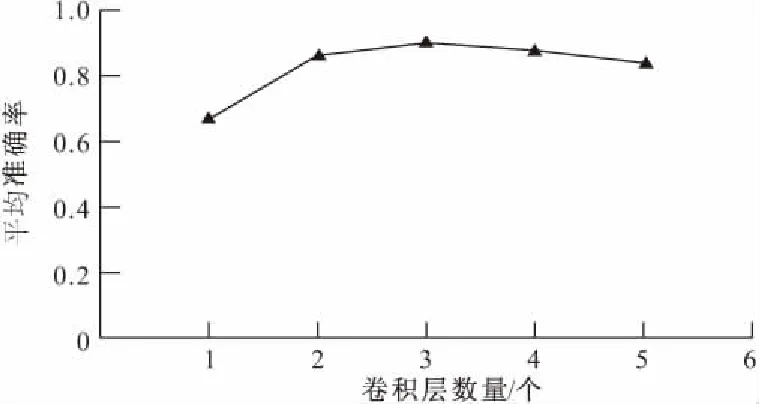
图7 不同卷积层数的分类结果

此外，分类的准确率会受迭代次数的影响，图8展示了不同迭代次数下的CNN平均识别准确率。因此本文推荐采用的迭代次数为5000～6000。

本文CNN基本架构如图9所示，第一层是大小为4×160的输入层，其中两个维度分别代表采样通道和采样数，随后每层节点数量均在图9中通过数字表示。在卷积操作C1～C2中均采用ReLU函数作为激活函数，池化层则采用最大值池化。在全连接操作中，L5～L7层采用Sigmoid激活函数，最后通过Softmax函数实现分类。由于Softmax的输出数据为输入样本在每个类别标签上的概率分布，因此为保证分类的准确性，选择分类正确概率超过60%的样本进行分类准确率的计算。整个模型的搭建和优化均在TensorFlow环境下进行，并选用梯度下降优化器，其实现代码为：train_step=tf.train.GradientDescentOptimizer(learning_rate).minimize(cross_entropy)(tf为Python语言下TensorFlow的缩写；train为调用命令的名称；GradientDescentOptimizer为选择使用梯度下降优化器；learning_rate为学习速率，本文学习速率为0.00001；minimize(cross_entropy)为使交叉熵最小化)。

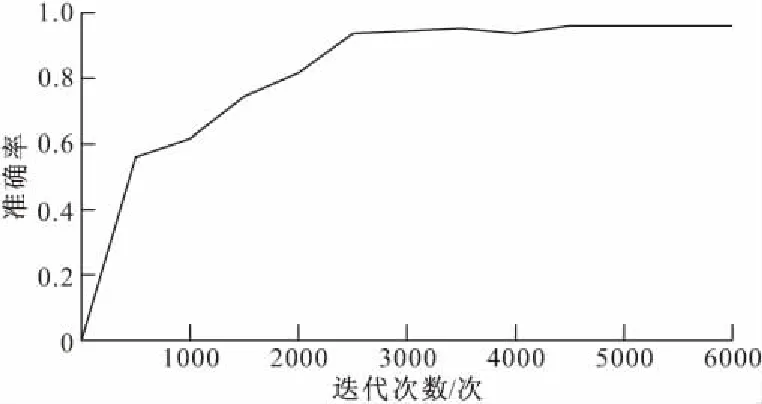
图8 不同跌代次数的分类结果

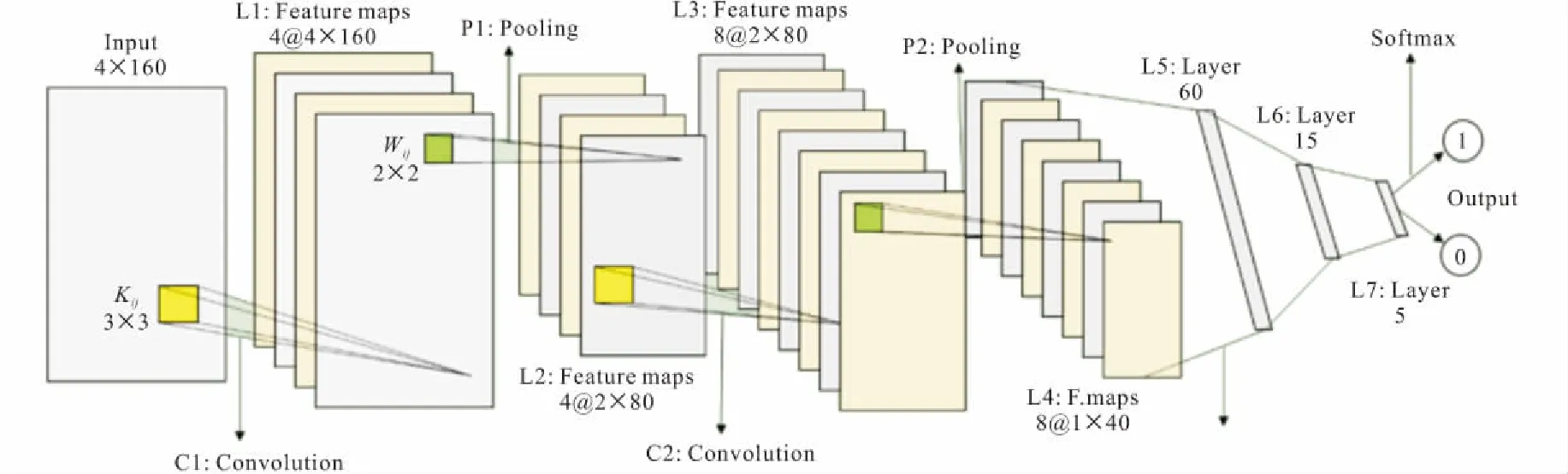
图9 CNN架构

3 数值试验

3.1 竖直悬臂梁模型

为研究激励类型对识别精度的影响规律和CNN特征提取的鲁棒性，本文利用ANSYS有限元软件建立了一个如图10所示的竖直悬臂梁模型。以下为本模型的基本参数：悬臂梁模型总共分为4个梁单元，以每个单元上部的节点作为采样点，由下而上分别编为1～4号。模型总高2.4 m，每个单元长0.6 m，弹性模量E=2.06×1011N/m2，截面面积为14.33 cm2，惯性矩I=243.98 cm4。结构的损伤通过折减单元的刚度模拟，即在原模型定义刚度EI上乘折减系数δ(δ是大小在0.5～1上的随机数，其中0.5表示刚度损失一半，1表示刚度未损失)，形成δEI。所有单元均设置损伤，因此每个样本中包含4个随机的刚度折减系数δ1～δ4。

为研究不同激励作用下CNN的识别精度，本文分别将随机的正弦激励、风激励以及白噪声激励作用到模型上。所有激励均是通过MATLAB软件随机生成，对于正弦激励，其振幅和频率均是服从正态分布的随机数。白噪声激励为满足正态分布的随机数。风激励则是根据Davenport风谱生成风速时程曲线，通过随机风速计算得到的随机风压，如式(5)所示。

(5)

式中：wp为风压；ρ为空气密度，其值取1.29 kg/m3；v为风速。

此外，激励的加载方式有所不同，正弦激励以集中力的形式作用在悬臂梁的顶端。风激励和白噪声激励则以均布荷载的形式作用在梁体上，如图10所示。

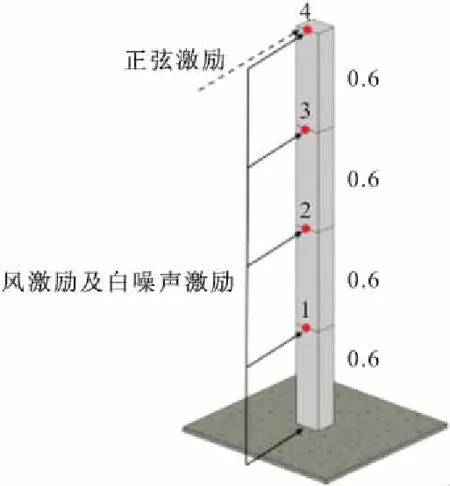
图10 竖直悬臂梁模型

通过上述操作，每个样本都是由不同大小、不同类型的激励作用生成的。每种激励生成2000个正常样本和2000个损伤样本作为CNN的训练集，另外生成相同数量的正常和损伤样本作为CNN的预测集。每个样本采集了悬臂梁模型上4个节点的加速度时程信号，采样时间为3.2 s，采样频率是50 Hz，因此将得到4×160的样本矩阵，如图11所示为不同激励作用下的加速度响应时程曲线。

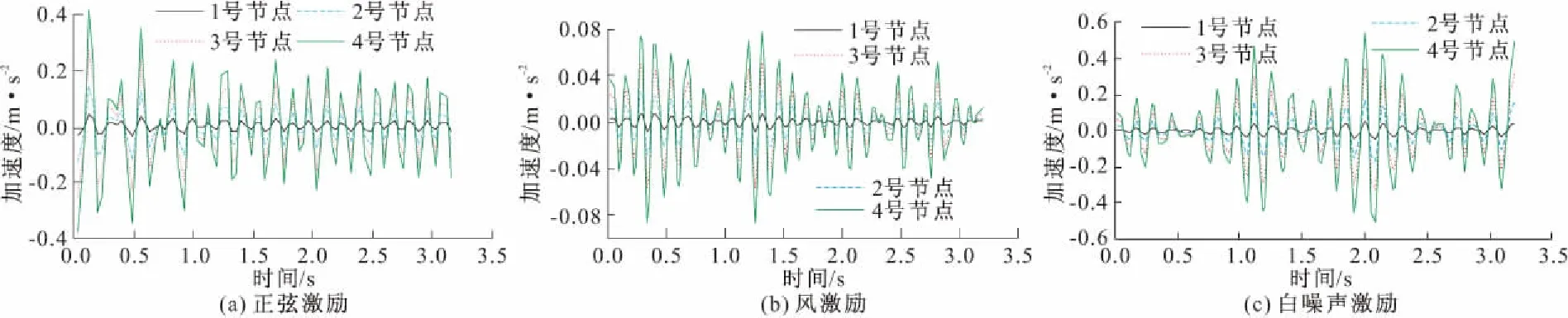
图11 数据集中的加速度信号(每个信号尺寸为4×160)

由于在实际情况下采集的振动信号是带噪的，为研究CNN的抗噪能力，本文进行了CNN抗噪性的仿真试验，根据式(6)所示信噪比对原始信号进行加噪，信噪比(Signal Noise Ratio, SNR)定义为：

(6)

3.2 结果分析

(1)在单激励无噪声训练模式下(即训练集中只有单一激励产生的加速度信号并且未加噪)，平均识别精度均稳定在90%以上，如图12a所示。采用混合激励训练模式(即训练集中混合各种激励产生的加速度信号的训练模式)时，CNN对正弦激励和风激励作用下结构损伤的识别精度没有明显影响。但是对白噪声激励作用下的平均识别精度有2%的提高，因此其平均识别率基本稳定在95%左右。具体情况如图12b所示。由此可见，虽然结构在不同激励作用下的各点加速度响应有明显差异(如图11所示)，但是这种差异不会影响到CNN对其损伤特征的提取，不同类型的激励及加载方式对CNN识别精度没有明显影响，且在采用混合激励训练模式后，相比于单激励训练模式，CNN的识别稳定性有一定的提高，其详细平均识别精度如表1所示。

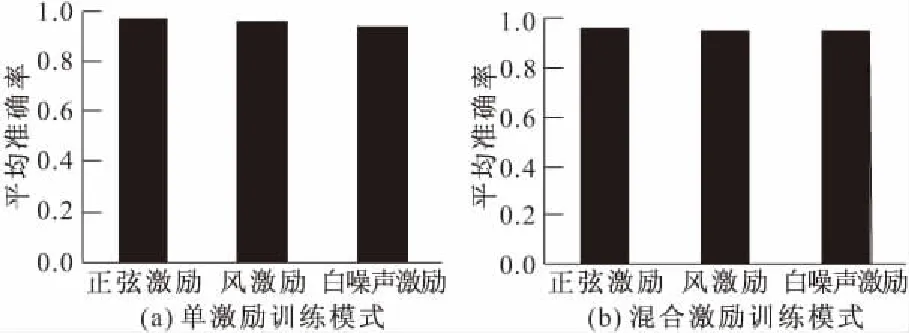
图12 不同训练模式下的CNN识别精度

表1 CNN平均识别精度

(2)如图13a所示，结构受正弦激励作用时，低强度噪声(SNR=10)对CNN的识别精度影响较小，基本可以忽略，其识别率均在95%以上，平均值为96%。随着噪声强度的增加，即当噪声强度增大到信噪比为5时，CNN的识别率受到较大影响，但也基本稳定在92%左右。当在添加了与加速度时程信号等能量强度，即SNR=1的噪声之后，CNN的平均识别准确率下滑到86%。可见，CNN对正弦激励作用下结构的损伤识别率呈现出线性下滑的态势。当结构受到风激励作用时，CNN的带噪识别精度如图13b所示。从图中可以看出，当SNR=10和5时，CNN的识别精度未受到显著影响，平均识别率从95%下降到92%。但是当噪声强度进一步升高到SNR=1时，其识别率出现了显著下降，但是其平均精度仍然保持在83%左右，其识别精度依旧令人满意，详细数据如表2所示。对于白噪声激励作用下结构的加速度信号其本身便可理解成噪声，因此本文在这里并未对其进行加噪研究。综上，在不同强度白噪声的作用下，CNN展现出了良好的抗噪能力，并且不同的激励类型对CNN的识别率没有明显影响。此外，CNN对不同激励之间的识别率虽略有差异，但是总体上均在可接受范围内，所以激励类型不是影响CNN识别精度的关键因素。

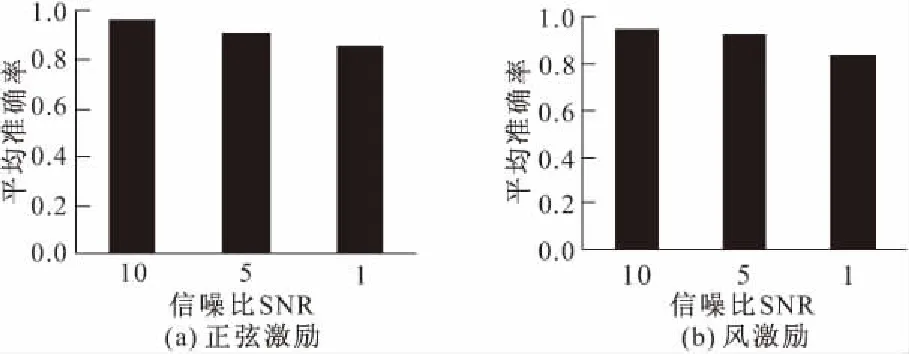
图13 CNN的带噪识别精度

表2 CNN带噪识别精度

(3)根据文献[6]的研究结果可知，混噪训练模式(即以不同强度噪声作为CNN的训练数据)可以有效地提高CNN的噪声容错区间，并且能更好地表达结构信息。如图14所示，采用混噪数据训练的CNN模型在整体识别率上高于单一噪声训练的模型，这也在一定程度上验证了文献[6]的结论。此外，通过混合训练模式(即混激励和混噪模式的结合，训练集中既包含了不同激励类型也包含了不同强度噪声)训练CNN，其平均准确率如图15所示。对比图14，发现相较于单一激励训练模式，混合训练的CNN识别率出现了小范围下滑，整体水平仍保持在90%左右。另外，在单激励训练模式下，随噪声强度的增加出现的识别率较大程度下滑，在混合激励训练模式下并未出现，可见通过混合激励训练模式，CNN模型的鲁棒性和稳定性在一定程度上得到了增强。其详细准确率数据如表3所示。

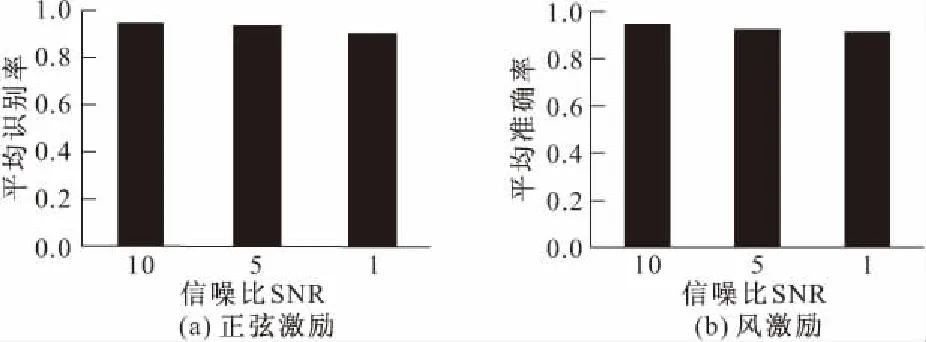
图14 混噪训练模式下CNN的识别精度

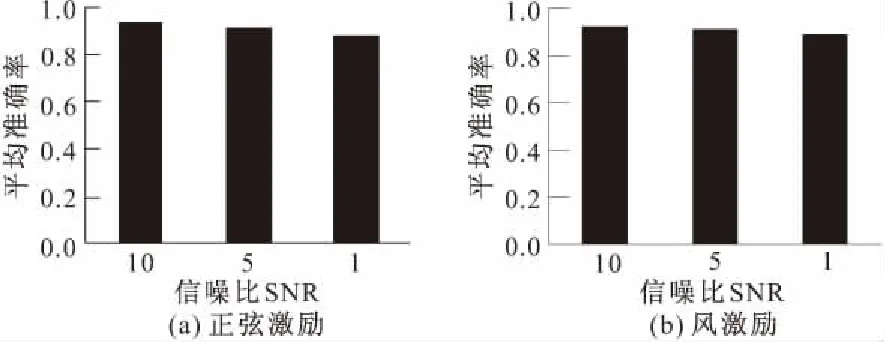
图15 混合训练模式下CNN的识别精度

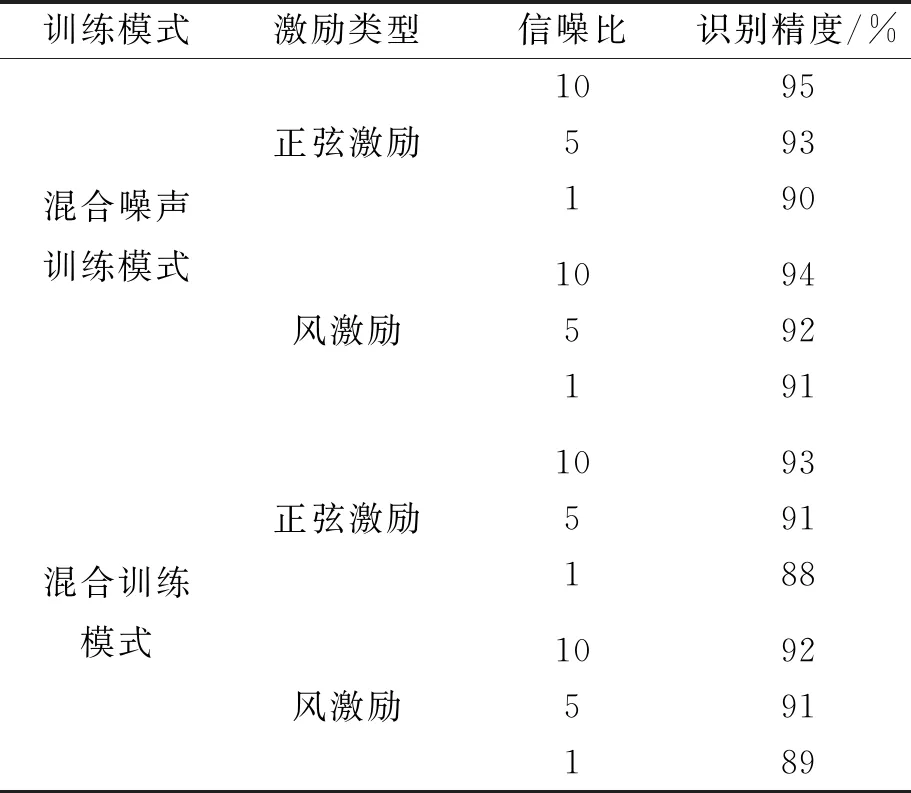
表3 不同训练模式下CNN带噪识别精度

(4)通过将瞬态响应和稳态响应分开训练，发现瞬态响应中应包含更为广阔的损伤特征信息。在激励作用下，由结构动力学原理可知，结构振动分为瞬态响应和稳定响应两种阶段。但因为阻尼的存在，瞬态响应会很快衰减，最终只呈现出稳态响应，如图16所示，虚线框内为瞬态响应，实线框内为稳态响应。

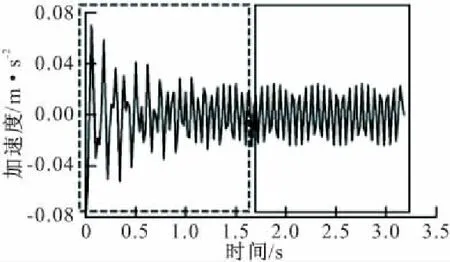
图16 正弦激励下结构加速度响应

因此，分别将带有瞬态响应的信号和不带瞬态响应的信号作为输入训练CNN。结果如图17所示，在迭代步同为2000时，有瞬态响应信号的网络识别率已经非常可观，平均精度稳定在96%，而不带瞬态信号的网络识别率仅仅为68%。但是当迭代步数为6000时，后者识别率依然可以达到93%。

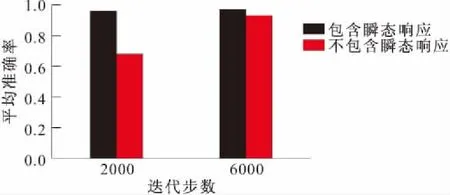
图17 不同训练阶段准确率

4 结 论

本文建立了一个简化的结构有限元模型，利用CNN在二维信号处理上的独特优势对4点的加速度信号进行自动特征提取并分类。研究发现，虽然在不同类型激励作用下，CNN的识别精度略有不同，但是整体来讲对CNN的识别准确率没有明显影响。并且，混激励训练可以在一定程度上提高CNN对不同激励的识别稳定性。因此，激励的类型不是影响CNN识别精度的主要因素。

在单激励训练模式下，CNN表现出了良好的抗噪性，但是对于不同噪声强度，其稳定性相对较差。采用混噪训练模式后，CNN的识别稳定性有了较为明显的改善。采用混合训练模式时，发现CNN的识别精度相较于混噪训练模式出现了小幅下降，但是其稳定性得到了提升，总体上识别率均稳定在90%左右。

此外，相较于稳态响应，瞬态响应包含了更广阔的损伤特征，而CNN可以对这些特征进行有效提取。并且在训练集中加入瞬态响应可以使网络的训练速率加快。另外，尽管稳态响应中包含的特征不如瞬态响应广阔，但是同样可以有效反应结构的损伤情况。

目前，CNN对结构的损伤诊断尚处于起步阶段，对用于诊断结构损伤的CNN架构及其参数设计仍是一个较大的挑战，目前只能通过试验验证法确定，因此本文所选取的超参数未必为最优参数。但是，从上述结果来看，CNN在结构损伤诊断方面的应用还大有可为之处。